Paraboloide Hiperbólico (HYPAR)

é a superfície gerada pela translação de uma parábola sobre outra parábola, sendo que as parábolas tem curvaturas opostas
Se as duas parábolas tiverem a mesma distância focal ,
o paraboloide hiperbólico é dito equilátero.
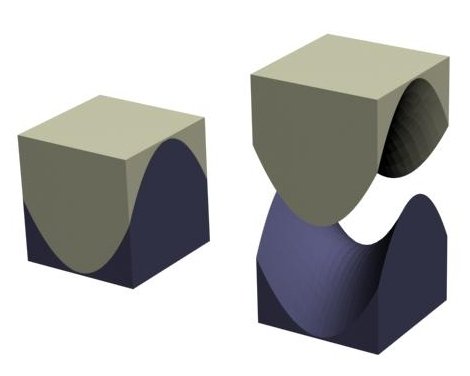
um HYPAR é uma superfície côncava ou convexa?
Superfície côncava ou convexa?
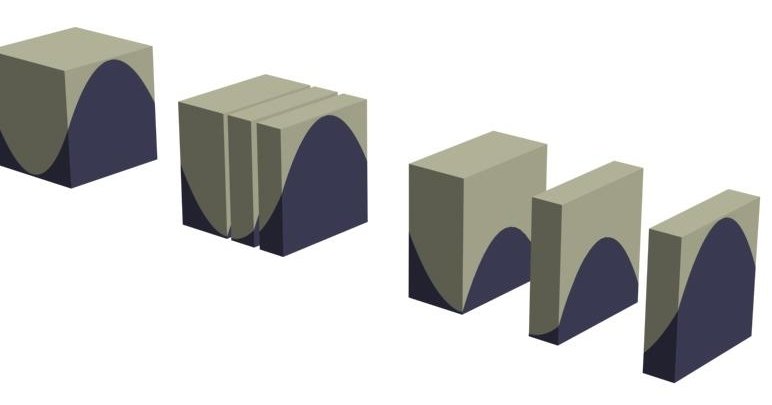
azul convexo

azul côncavo
e se cortarmos a 45 graus?
cortes à 45 graus de um HYPAR equilátero
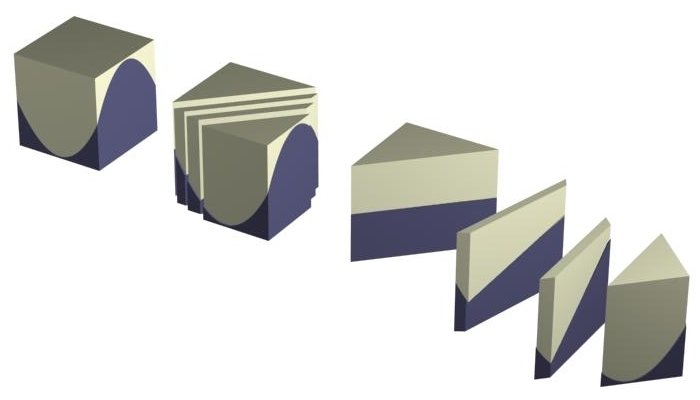
mas por que estes paraboloide são chamados de hiperbólicos?
cortes perpendiculares ao eixo do HYPAR
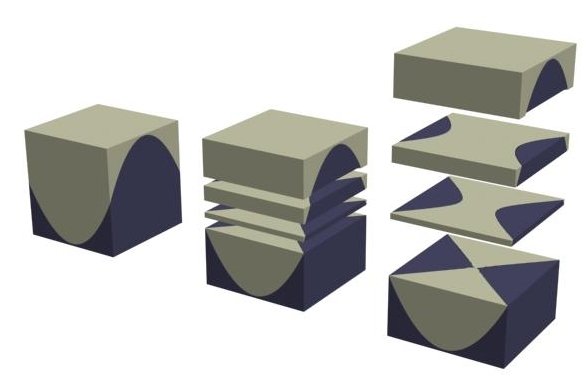
na realidade as supercífies são classificadas de acordo com sua curvatura gausseana (K = k1 x k2) como:
Superfície plana:
k1= 0 e k2 =0
Superfície de curvatura simples:
K= 0 (k1 ou k2 =0) (desenvolvíveis)
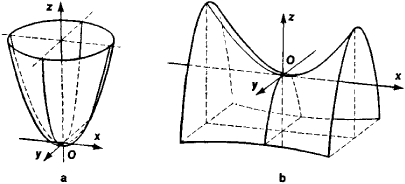
Superfícies de dupla curvatura para o mesmo lado:
K>0 = elipticas = sinclásticas
Superfícies de dupla curvatura para lados opostos:
K<0 = hiperbólicas = anticlásticas
HYPAR é uma superfície regrada
(pode ser construida apenas por linhas retas)

mas não é uma superfície desenvolvível
(as normais mudam de direção ao longo de uma reta)
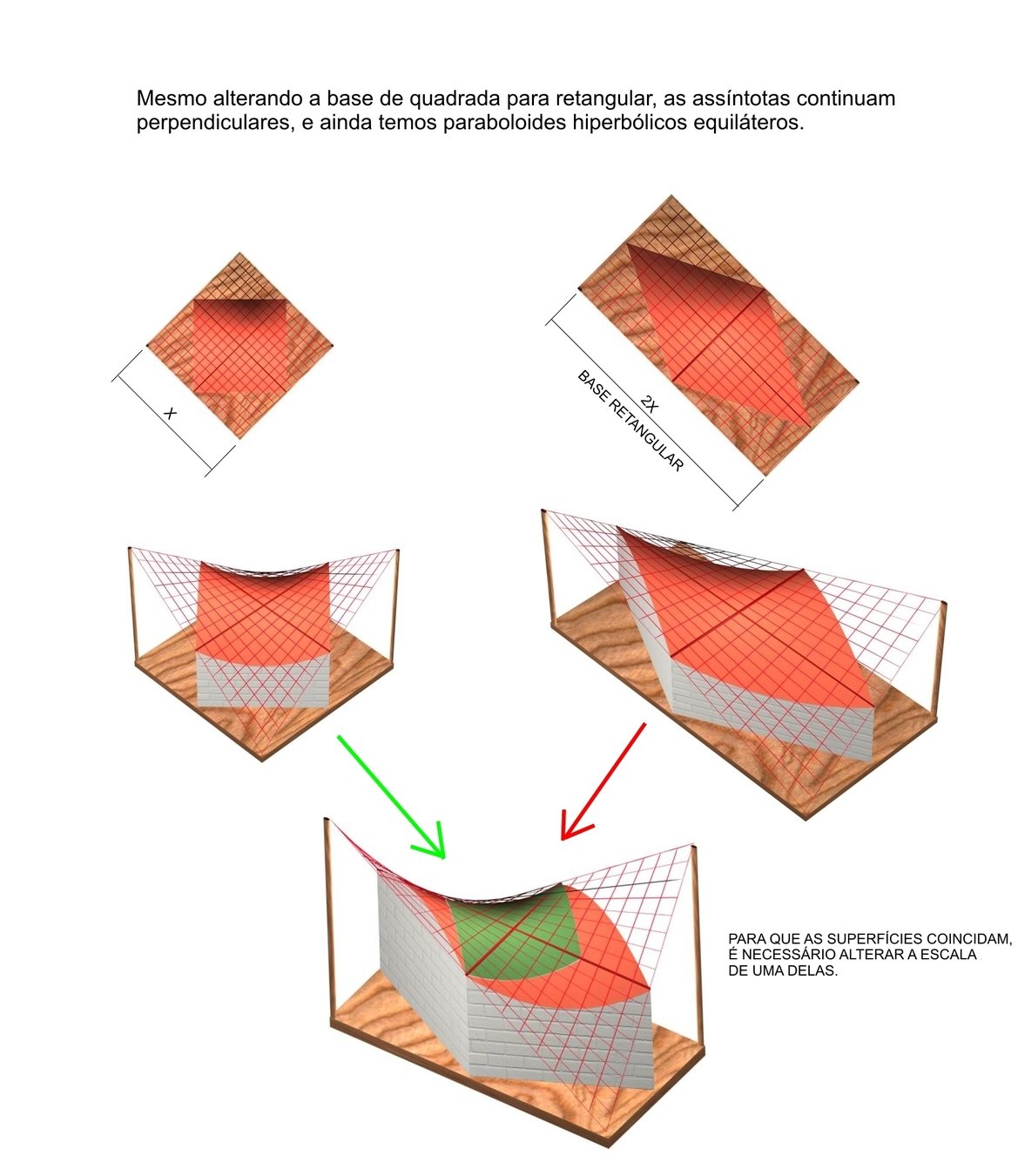
HYPAR não equilátero
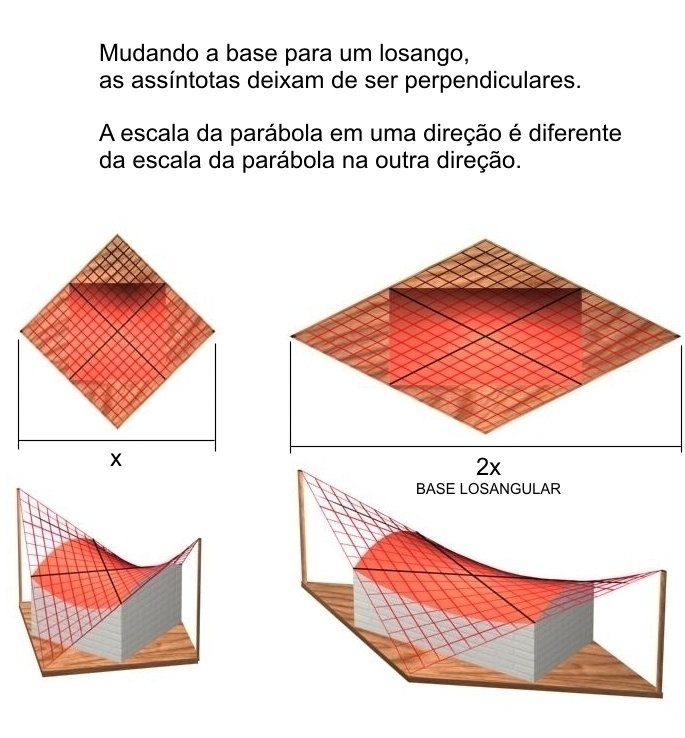
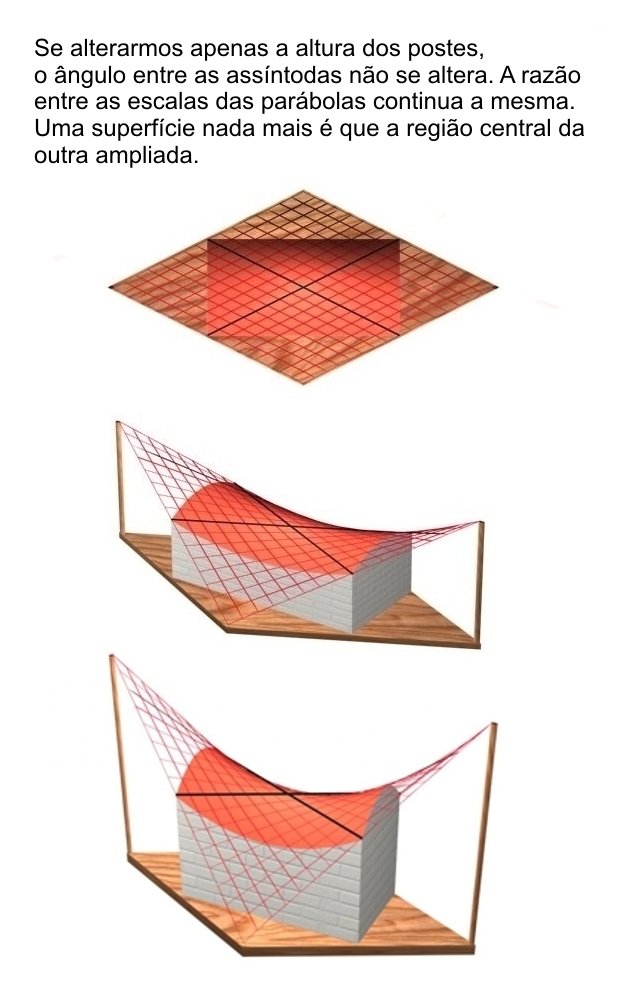
o comprimento das retas variam,
as maiores passam pelos vértices do paraboloide.

dependendo de como se corta a superfície o HYPAR pode ter vários aspectos:



Felix Candela





O maior HYPAR do mundo

Obras



Ache o HYPAR


Antoni Gaudi
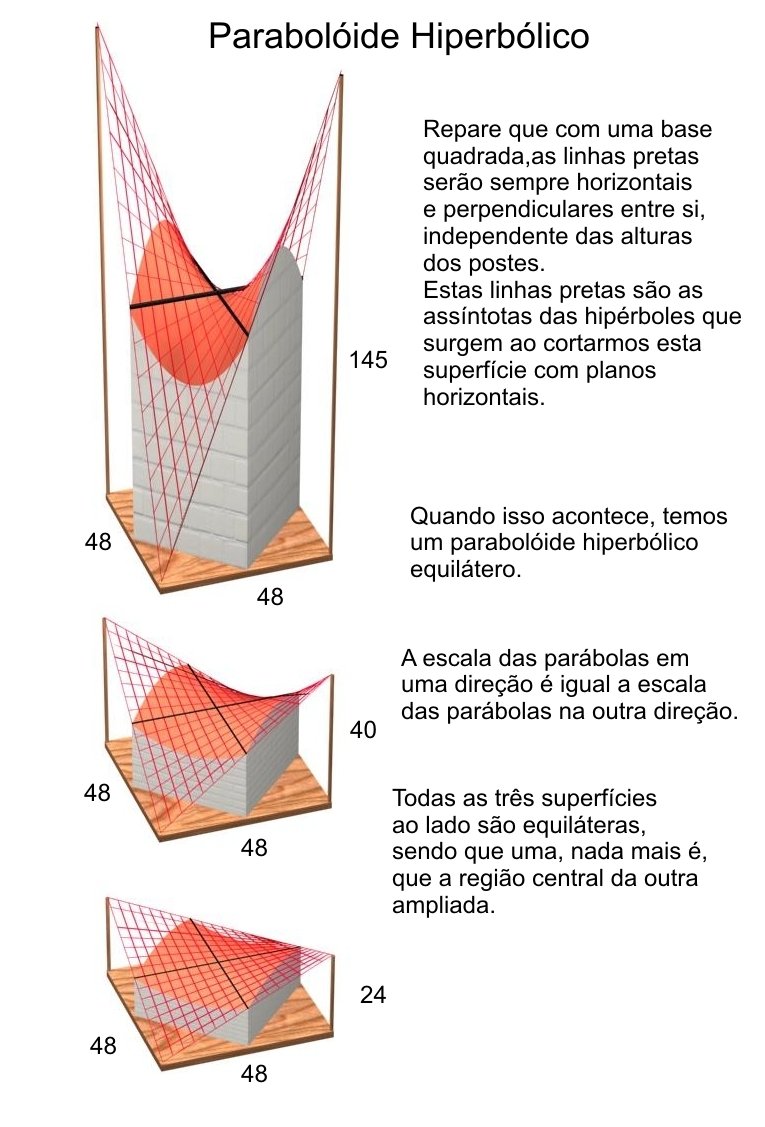
Parabolóide Hiperbólico
By Charlot Fantasias
Parabolóide Hiperbólico
- 83



