Na última aula você viu...
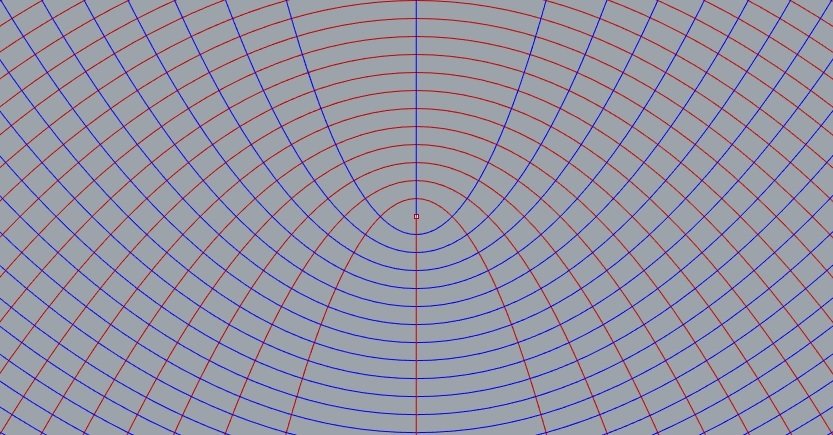
que parábolas cofocais se cruzam a 90°
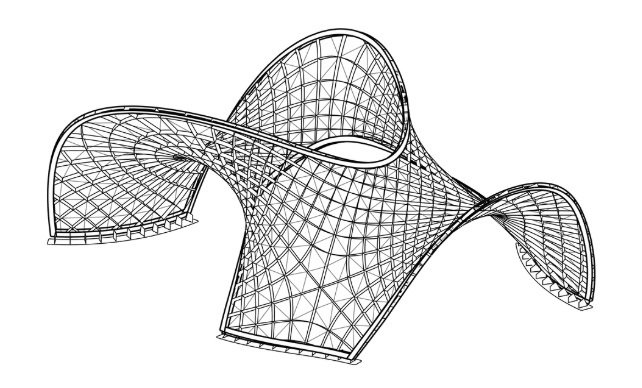
a apresentação do pavilhão assintótico
(lâminas retas e cruzamentos a 90°)

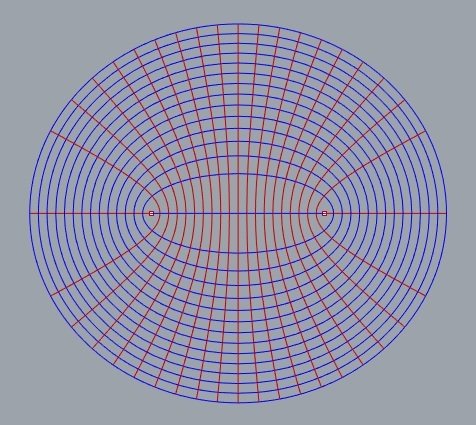
que elipes e hiperboles cofocais se cruzam a 90°
agora ao invés das curvas, exploraremos as superfícies do 2° grau
Superfícies quádricas

paraboloide elíptico
paraboloide hiperbólico
elipsoide
hiperboloide de 1 folha
hiperboloide de 2 folhas
(superfície do 2° grau)
Superfícies quádricas na arquitetura



paraboloides

Superfícies quádricas na arquitetura



elipsoides
Superfícies quádricas na arquitetura


hiperboloides
Paraboloides
paraboloide elíptico
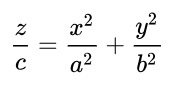
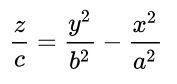
paraboloide hiperbólico

Desenhando um paraboloide elíptico
- revolução de uma parábola pelo eixo de simetria
- deformando a superfície anterior
- translação de uma parábola sobre outra parábola
- superficie NURBS com 9 pontos (3x3)
- através de equações (grasshopper)
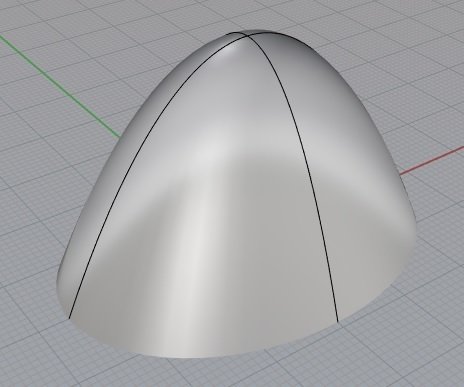
Desenhando um paraboloide hiperbólico
- superfície por 4 pontos (regrada)
- translação de uma parábola sobre outra parábola
- superficie NURBS com 9 pontos (3x3)
- através de equações (grasshopper)

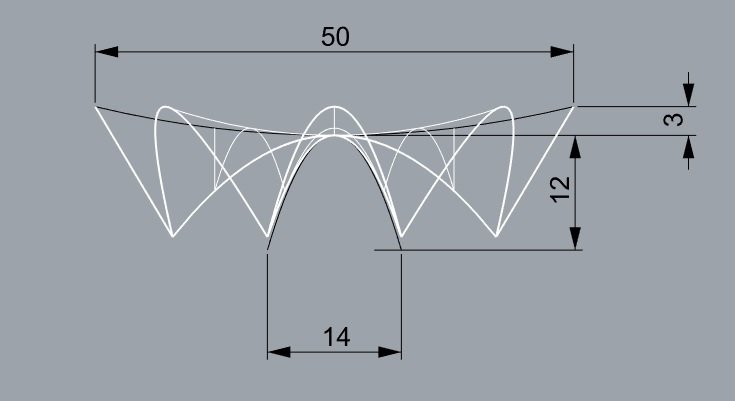
Paraboloide hiperbólico
o que muda quando desenhado por métodos diferentes?
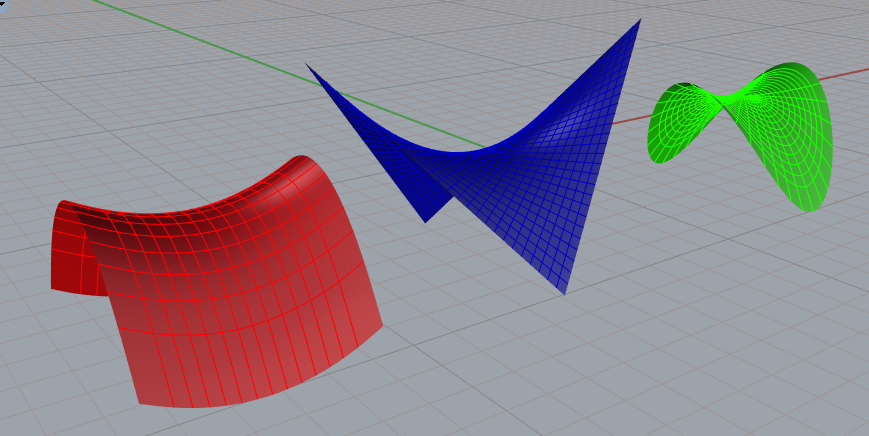
isocurvas (U e V)



Aquário de Valência
Félix Candela


Laboratório de Raios Cósmicos
Félix Candela




Usinagem de um paraboloide eliptico na Router CNC do LAME
elipsoides e hiperboloides
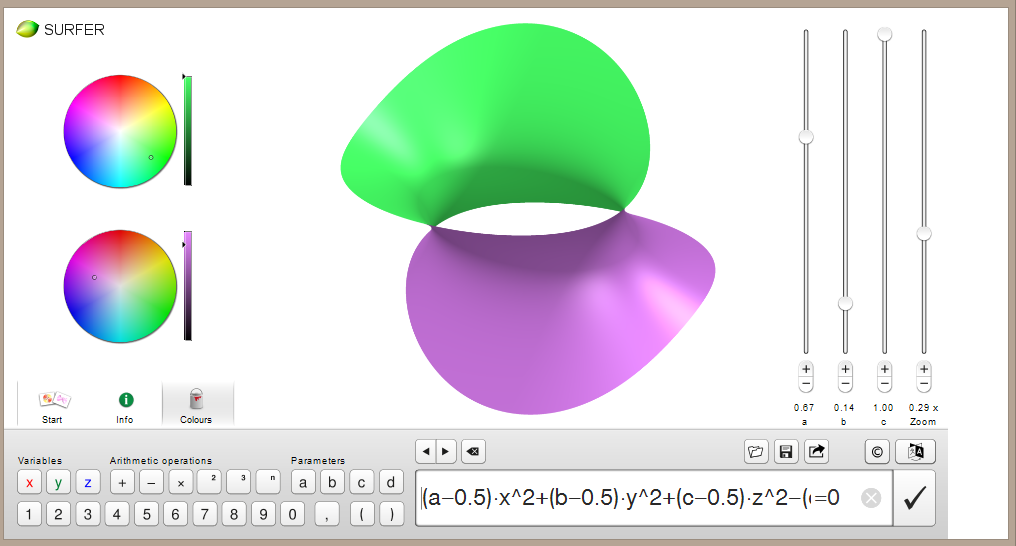
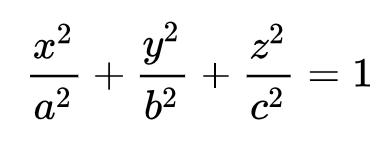
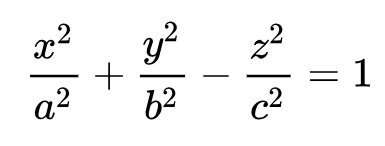
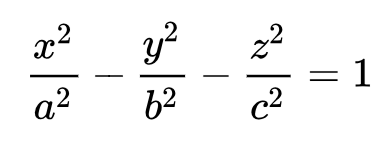
elipsoide
hiperboloide 1 folha
hiperboloide 2 folhas
Desenhando um elipsoide

- deformando uma esfera
- revolução de uma elipse pelo eixo maior (prolato)
- revolução de uma elipse pelo eixo menor (oblato)
- deformando a forma de revolução anterior (escaleno)
- usando o comando nativo do Rhino
- através de equações (grasshopper)
Desenhando um hiperboloide de 1 folha
- revolução de uma hipérbole (eixo imaginário)
- revolução de uma reta (superfície regrada)
- deformando as superfícies de revolução anteriores
- varredura de uma elipse por 2 trilhos (hipérbole)
- através de equações (grasshopper)

Desenhando um hiperboloide de 2 folhas
- revolução de uma hipérbole (eixo real)
- deformando a superfície anterior
- varredura de uma elipse por 2 trilhos (hipérbole partida)
- através de equações (grasshopper)

A superfície gerada pela translação de uma hipérbole sobre outra hipérbole, não é uma quádrica (2° grau).
CUIDADO !
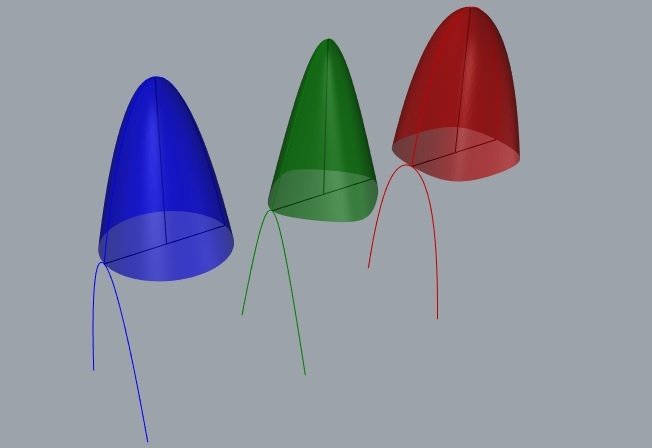
parábola
hipérbole
catenária
Relembrar é viver...

agora faremos algo similar mas em 3D
todas as intersecções entre elipses e hipérboles cofocais, se dão a 90°
elipsoides e hiperboloides cofocais
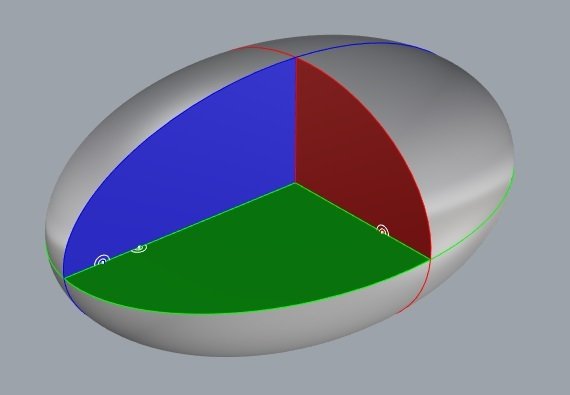

Se cada secção plana é uma elipse diferente, com seus respectivos focos, como desenhar elipsoides e hiperboloides cofocais ?
Onde estão os focos de um elipsoide?
Desenhando elipsoides e hiperboloides cofocais




todas as superfícies se cruzam ortogonalmente
Elipsoide de Monge


Gaspard Monge
As linhas (principais de curvatura) também podem ser desenhadas pelo método do jardineiro com as estacas fincadas nos pontos umbílicos.
ponto umbílico
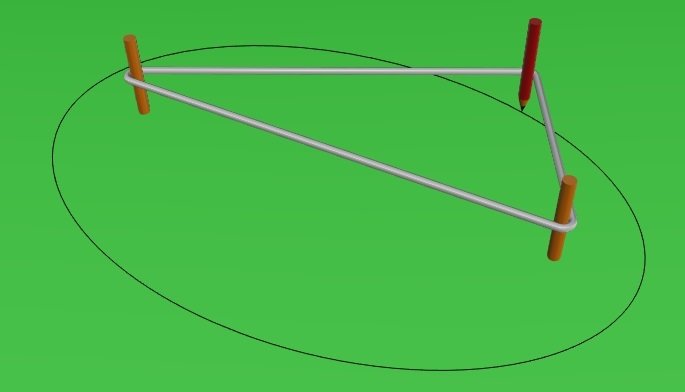



O teorema de Ivory continua válido em 3D
Em cada "quadrilátero" as diagonais tem o mesmo comprimento e são coplanares.
Os vértices dos "quadrilátero" são coplanares.

o que permite a construção de um elipsoide com painéis planos
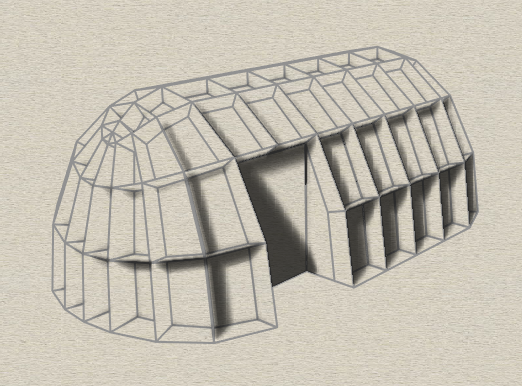


Fabricando um elipsoide de Monge em madeira




cúpula elipsoidal pelo método de Monge
Ele acreditava que estas linhas eram ideais para o corte das pedras na arte da estereotomia.
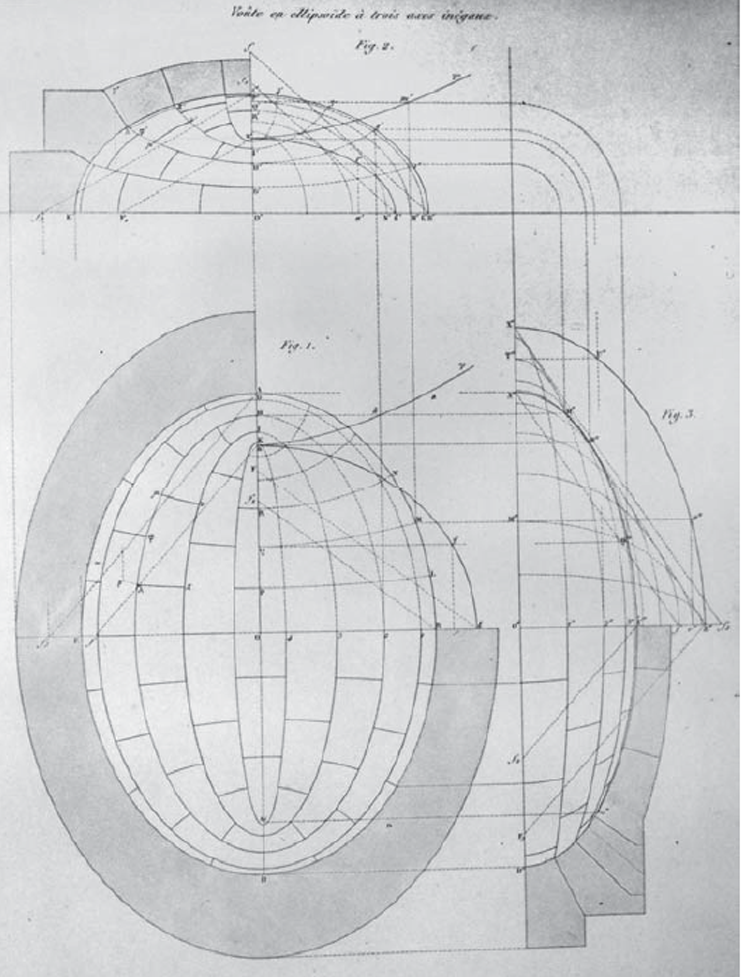
Monge descobriu um método brilhante, que agiliza o desenho das projeções das linhas principais de curvatura de um elipsoide.

A Biblioteca da FAU possui o livro "Traité de Stéréotomie" (Leroy, Charle François), impresso em 1910 pela École Polytechnique de Paris, onde o método de Monge é explicado.
O livro pertenceu ao Prof. Luiz Ignácio de Anhaia Mello.

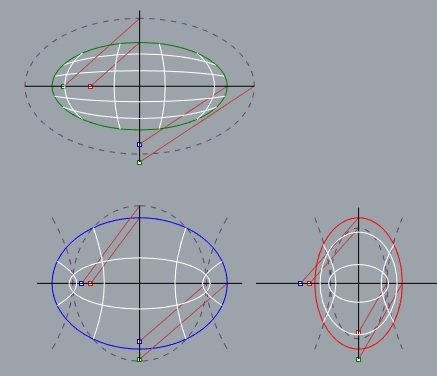
Monge facilitou o trabalho em 2D...
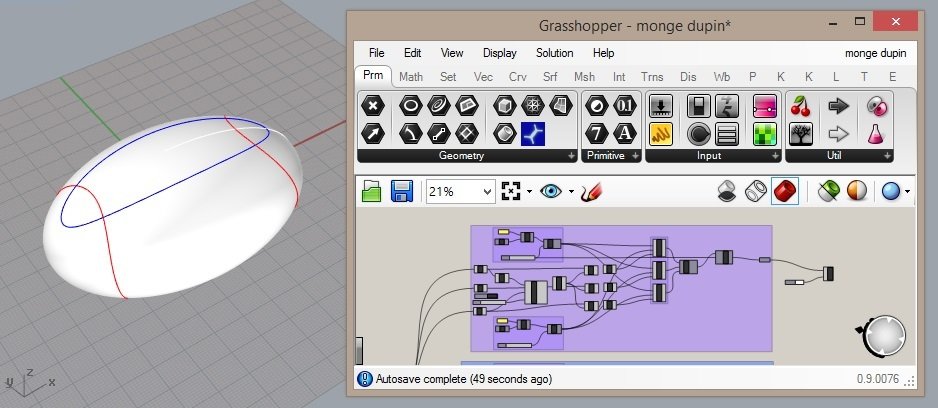
como a vida ficou fácil, agora é possível contruir o ...
mas e em 3D?

modelo 3D da cúpula elipsoidal de Monge
Superfícies Triortogonais (Raio X)
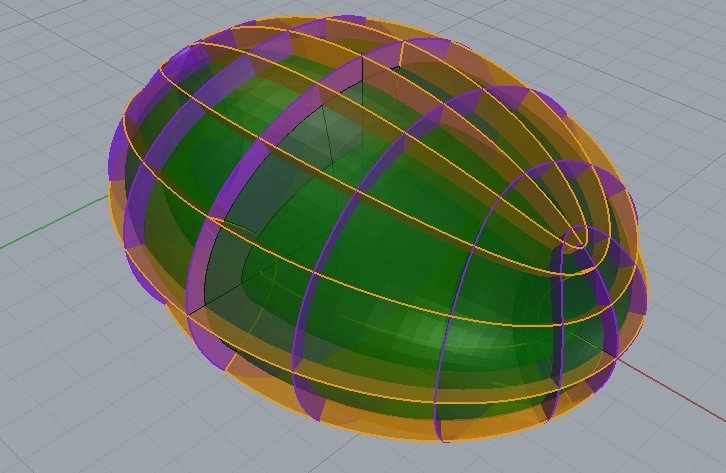
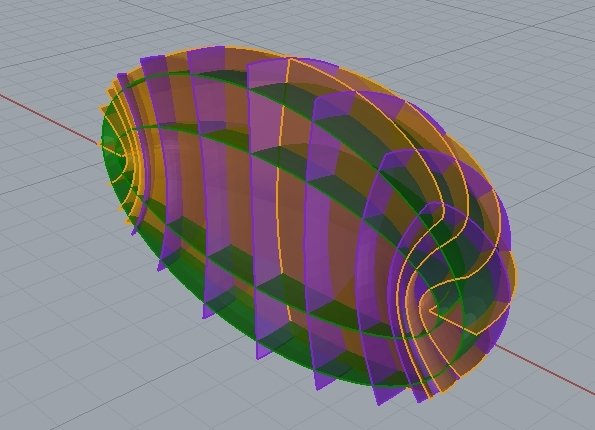


elipsoides
hiperboloides 1 folha
hiperboloide 2 folhas

Resumindo
elipsoides
hiperboloides 1 folha
hiperboloide 2 folhas
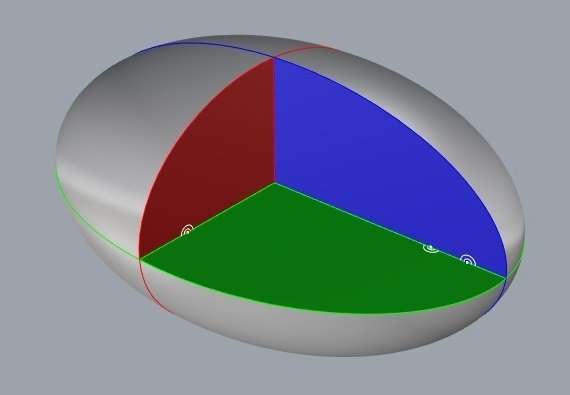
Teorema de Dupin

Em um sistema de superfícies triortogonais, as linhas principais de curvatura de uma superfície, resultam das intersecções desta superfície com as superfícies das outras duas famílias.
elipsoides
hiperboloides 1 folha
hiperboloide 2 folhas
Charles Dupin

ponto umbilico do elipsoide
ponto umbilico do hiperboloide de 2 folhas
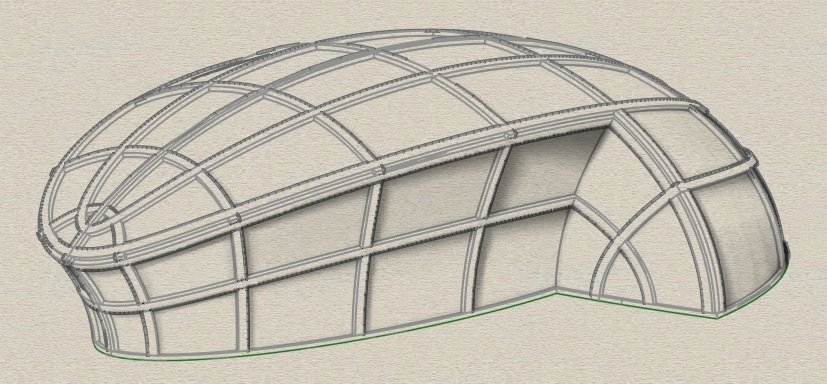
Tanto a superfície formada pelas normais quanto a superfície tangente a uma linha principal de curvatura são desenvolvíveis.

superfície normal
superfície tangente
- linhas principais de curvatura
- linhas geodésicas
- linhas assintóticas
- superfícies mínimas
Próxima aula:
Em breve veremos que as linhas com estes poderes "mágicos" (linhas principais de curvatura) podem ser traçadas sobre qualquer superfície e não apenas em sistemas triortogonais.
Superficies Quádricas
By Charlot Fantasias
Superficies Quádricas
elipsoides, paraboloides e hiperboloides
- 2,525



