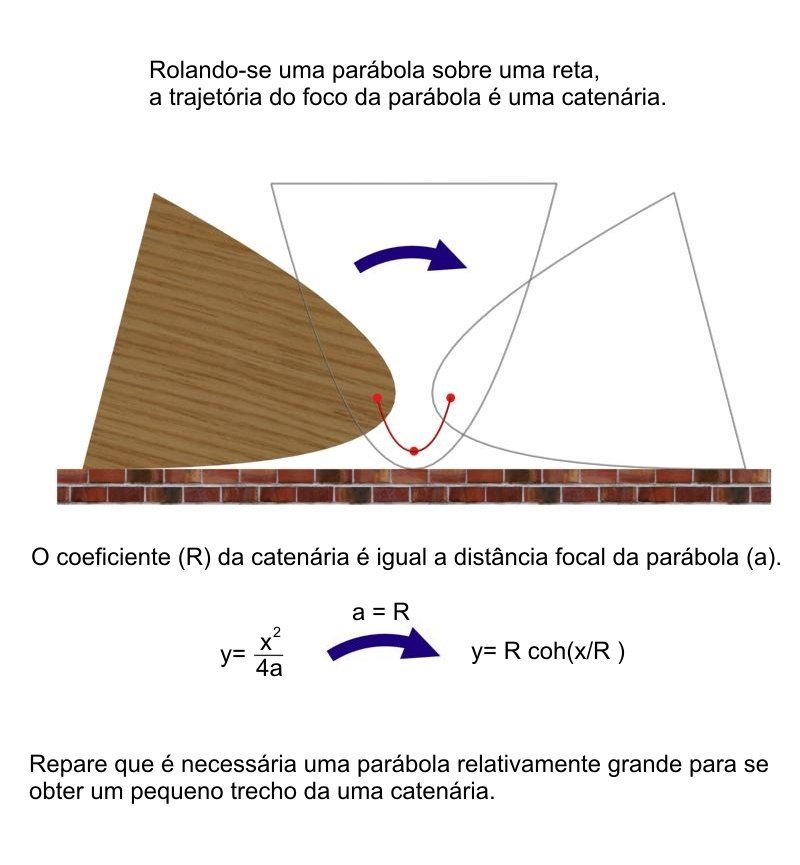
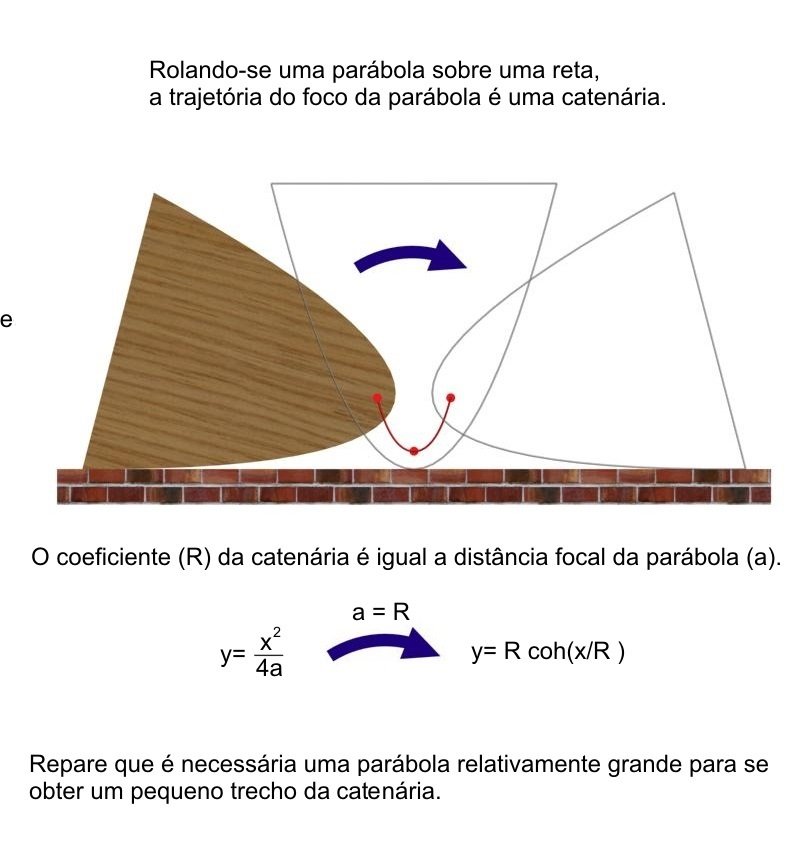
Catenária vs Parábola
Por serem parecidas, Galileu Galilei, acreditava tratar-se da mesma curva.


Em 1690 Huygens, Leibniz e John Bernoulli, descobrem a equação da catenária.
y = a cosh (x/a)
y = x / 4a
2
Catenóide
Em 1744 Leonhard Euler, descobre o catenóide,
a única superfície mínima de revolução.

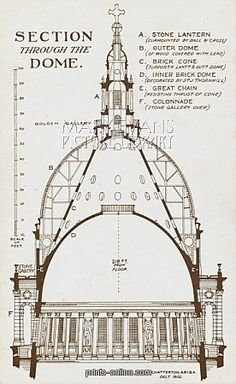
Em 1675 Robert Hooke mostra que fios tracionado com pesos pendurados quando invertido dão a forma de um arco sobre compressão.
O arquiteto Sir Christopher Wren projeta o domo da catedral de St.Paul em Londres usando o método funicular de Hooke.
Antoni Gaudi (1852 - 1926)
usou o sistema funicular em muitas de suas obras.

Em 2000 Norman Foster projeta o teto do museu britânico usando um programa de form finding
(relaxamento dinâmico).




Gateway Arch - St. Louis - Missouri - USA
Catenária ou Parábola?
Apesar de ser uma parábola, as duas curvas ficam muito parecidas
quando o vão é bem maior que a flecha.

Catenária ou Parábola?
Catenária ou Parábola?


Apesar do cabo ser bem pesado, o peso da pista é bem maior.
Parece mas não é!!!

Catenária é uma curva única, só varia a escala.
LCC

Planetário Ibirapuera
Gateway St Louis

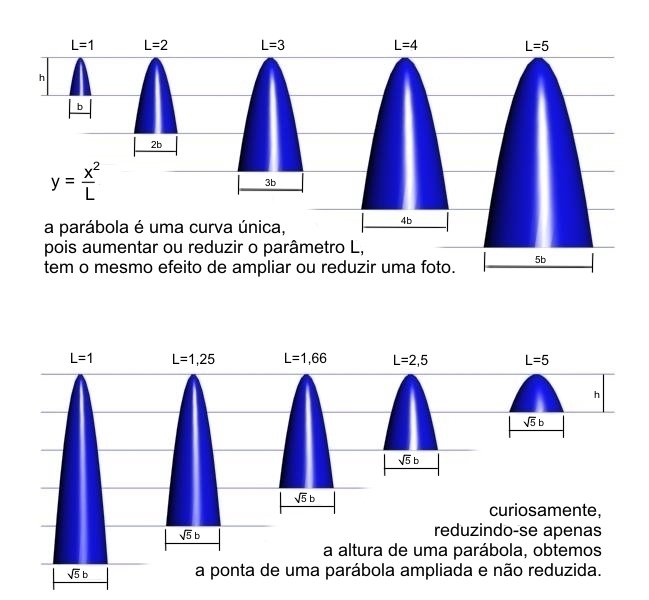
Mudando a escala em apenas um dos eixos
Parábola continua sendo parábola
Catenária deixa de ser catenária
Para se desenhar uma catenária você pode:

usar uma corrente pendurada
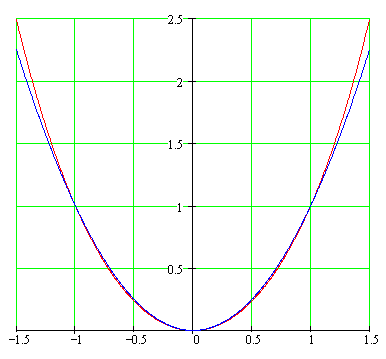
plotar o gráfico da função:
y = a cosh (x/a)
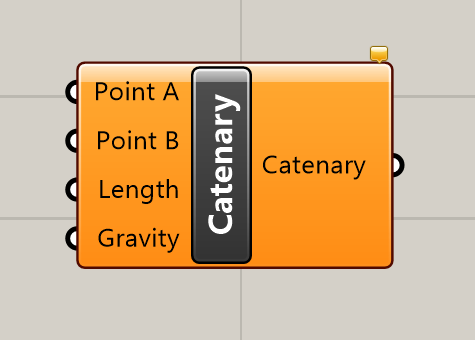
usar um comando específico
de um programa de CAD

simular uma corrente em um sistema de form finding
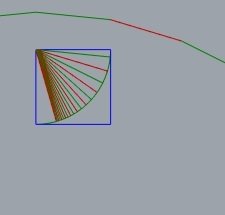
usar o método da régua e compasso
Catenária vs Parábola
By Charlot Fantasias
Catenária vs Parábola
- 80



