Cryptocurrencies & Blockchain Techs
What is money?
- A medium of exchange
- A unit of account
- A store of value
- A standard of deferred payment
How to create money?
- M0: cash money created by a central bank by minting coins and printing banknotes
- M1/M2: money created by private banks through the recording of loans as deposits of borrowing clients
- Currently created as electronic money
Rai stones from Yap

Bitcoin
- A cryptocurrency invented by Satoshi Nakamoto
- Verified transactions are recorded in a public distributed ledger
- A decentralized digital currency
Key technologies
- Ownership established using digital signatures
- Transaction history in tamper-evident logs, a.k.a. blockchains
- Decentralization via consensus protocols
Digital signatures
The cannonball problem

The method of Diophantus
- \(1^2+2^2+\cdots+x^2=\frac{x(x+1)(2x+1)}{6}=y^2\)
- Two trivial solutions: \((x,y)=(0,0)\) or \((1,1)\)
- The line through these two points is \(y=x\), which intersects with the curve and gives the equation \[x^3-\frac{3}{2}x^2+\frac{1}{2}x=0\]
- The third root is \(x=\frac{1}{2}\)
Repeat for (1,1) & (1/2,-1/2)
- The line is \(y=3x−2\), so the equation is \[x^3-\frac{51}{2}x^2+\cdots=0\]
- The third root is \(x=24\), so \(y=70\), i.e., \[1^2+2^2+\cdots+24^2=70^2\]
- If we keep repeating this procedure, we'll obtain infinitely many rational solutions to our equation
- However, it can be shown that \((24,70)\) is the only non-trivial solution in positive integers
The congruent number problem
- The question of which integers \(n\) can occur as areas of right triangles with rational sides is known as the congruent number problem
- E.g., \(n=5\): are there rational numbers \(a,b,c\) s.t. \[a^2+b^2=c^2,ab=10?\]
- Equivalently, \(c^2+20=(a+b)^2,c^2-20=(a-b)^2\)
- Let \(x=(c/2)^2\): \(y^2=(x+5)x(x-5)=x^3-25x\)
Diophantus revisited
- Consider the tangent line at \((−4,6)\): \(y=\frac{23}{12}x+\frac{41}{3},\) which intersects the curve and gives \[x^3-\left(\frac{23}{12}\right)^2x^2+\cdots=0\]
- The third root is \((23/12)^2+4+4=(41/12)^2\), i.e., \[a=\frac{20}{3},b=\frac{3}{2},c=\frac{41}{6}\]
- There are infinitely many other solutions, which can be obtained by successively repeating this procedure
An elliptic curve \(E\) is the graph of an equation of the form \(y^2=x^3+Ax+B\), where \(A\) and \(B\) are constants. This will be referred to as the Weierstraß equation for an elliptic curve. We will need to specify what set \(A,B,x\) and \(y\) belong to. Usually, they will be taken to be elements of a field, for example, the real numbers \(\mathbb R\), the complex numbers \(\mathbb C\), the rational numbers \(\mathbb Q\), one of the finite fields \(\mathbb F_p(=\mathbb Z/p\mathbb Z)\) for a prime \(p\), or one of the finite fields \(\mathbb F_q\), where \(q=p^k\) with \(k\geq 1\). If \(K\) is a field with \(A,B\in K\), then we say that \(E\) is defined over \(K\).
Points on elliptic curves
- If we want to consider points with coordinates in some field \(L\supseteq K\), we write \(E(L)\)
- By definition, this always contains the point at infinity: \[E(L)=\Big\{\infty\Big\}\bigcup\Big\{(x,y)\in L\times L:y^2=x^3+Ax+B\Big\}\]
- \(E(L)\) is an abelian group
Group operations in \(E(L)\)

Elliptic curve cryptography
- Security depends on the hardness of the elliptic curve discrete logarithm problem (ECDLP)
- Given a point \(Q\in G\subseteq E(L)\) and a generator \(P\) of \(G,\) find an integer \(n\) s.t. \(nP=Q\)
- Pros: smaller keys and ciphertexts for achieving same security level as DLP-based cryptosystems
- \(\text{160--256}\) bits vs. \(\text{1024--3072}\) bits
- Cons: security is achieved only over secure curves
ECDSA
- To sign a message \(m\):
- \(h\leftarrow H(m)\)
- \(k\stackrel{\$}{\leftarrow}(\mathbb Z/q\mathbb Z)^*\)
- \(\color{blue}r\color{black}\leftarrow f(kP)\bmod q\)
- \(\color{blue}s\color{black}\leftarrow(h+\color{red}x\color{blue}r\color{black})/k\bmod q\)
- To verify signature \(\color{blue}(r,s)\):
- \(h\leftarrow H(m)\)
- \(a\leftarrow h/\color{blue}s\color{black}\bmod q\)
- \(b\leftarrow \color{blue}r\color{black}/\color{blue}s\color{black}\bmod q\)
- \(f(aP+bQ)\stackrel{?}{=}\color{blue}r\color{black}\bmod q\)
Why it works? \[f(aP+bQ)=f(aP+b\color{red}x\color{black}P)=f(\frac{h+\color{red}x\color{blue}r\color{black}}{s}P)=f(kP)\]
Digital signatures in Bitcoin
- ECDSA over curve secp256k1
- Public/private keys: 33 or 65 bytes
- Signatures: 71, 72, or 73 bytes
- Bitcoin address = RIPEND160(SHA256(pk)): 20 bytes
- Often in Base58Check encoding
Bitcoin transactions
- Transactions consist of \(\geq 1\) inputs and \(\geq 1\) outputs
- To prevent double spending, each input must refer to a previous unspent transaction output (UTXO)
- Except for coin generation, e.g.: genesis block
Hash function
-
One-way function
- A function \(f\) that is easy to compute on every input \(x\), but hard to invert given the image \(f(x_0)\) of a random input \(x_0\)
- Ideal model: random oracle
- In practice: cryptographic hash function
- SHA-256, SHA-512
- SHA3 (Keccak)
Merkel tree
Blockchains as
tamper-evident logs
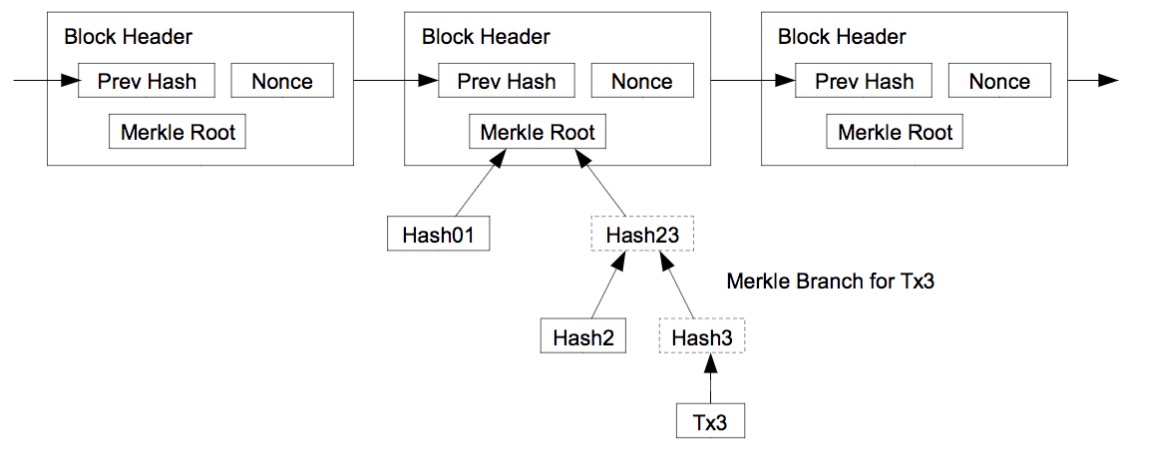
The Bitcoin consensus protocol
- New transactions are broadcast to all nodes
- Each node collects transactions into a block and broadcasts the block as its proof of work
- Other nodes accept the block only if all transactions in it are valid, i.e., unspent with valid signatures
- Nodes express their acceptance of the block by including its hash in the next block they create
Incentivization via mining
- Bitcoin miners' incentives
- Transaction fees
- Block rewards
- Started being 50 bitcoins in 2009, now 3.125
- Cut in half every 4 years to limit supply to ≈21M
- Best strategy: when there are multiple chains of blocks, follow the longest chain of blocks
| opcode | mnemonic | description |
|---|---|---|
| 0x01–0x4b | push next opcode bytes of data | |
| 0x69 | OP_VERIFY | if (pop() != true) then fail |
| 0x76 | OP_DUP | let x := pop() in push(x) push(x) |
| 0x87 | OP_EQUAL | push(pop() == pop()) |
| 0x88 | OP_EQUALVERIFY | = OP_EQUAL OP_VERIFY |
| 0xa9 | OP_HASH160 | push(RIPEND160(SHA256(pop()))) |
| 0xac | OP_CHECKSIG | verify signature |
Executing P2PKH scripts

- Pay-to-PubkeyHash
- scriptSig: <sig> <pubKey>
- scriptPubKey: OP_DUP OP_HASH160 <pubKeyHash?> OP_EQUALVERIFY OP_CHECKSIG
- Pay-to-ScriptHash
- scriptSig: ...signatures... <serialized script>
- scriptPubKey: OP_HASH160 <scriptHash> OP_EQUAL
Ethereum
- Proposed in late 2013 by Vitalik Buterin
- Went live on 30 July 2015
- Stewarded by nonprofit foundation
- Turing-complete scripts, a.k.a. smart contracts
- A contract is a program that lives on the blockchain
- A dApp is a collection of integrated contracts
- A decentralized autonomous organization (DAO) is an organization represented by rules encoded as contracts on a blockchain
An example contract
contract NameRegistry {
mapping(bytes32 => address) public registryTable;
function claimName(bytes32 name) {
if (msg.value < 10) {
throw;
}
if (registryTable[name] == 0) {
registryTable[name] = msg.sender;
}
}
}Opportunities
- Electronic payment
- Asset tokenization
- Provenance tracking
- Digital identity
- Custody & escrow
- Automation
Challenges
- Operating models and regulation
- Scalability
- Privacy
- Latency
- Integration
Lack of privacy on blockchains
- \(H(x)\) is a "proof" of \(x\)
- To verify, however, need to reveal \(x\)
- Zero-knowledge proofs:
- Can prove without revealing \(x\)
Questions or comments?
Blockchains: Bitcoin and beyond
By Chen-Mou Cheng
Blockchains: Bitcoin and beyond
- 922



