Soss: Probabilistic Metaprogramming in Julia

Chad Scherrer
Senior Data Scientist, Metis

Making Rational Decisions
Managed Uncertainty
Rational Decisions
Bayesian Analysis
Probabilistic Programming
- Physical systems
- Hypothesis testing
- Modeling as simulation
- Medicine
- Finance
- Insurance
Risk
Custom models
A Simple Example
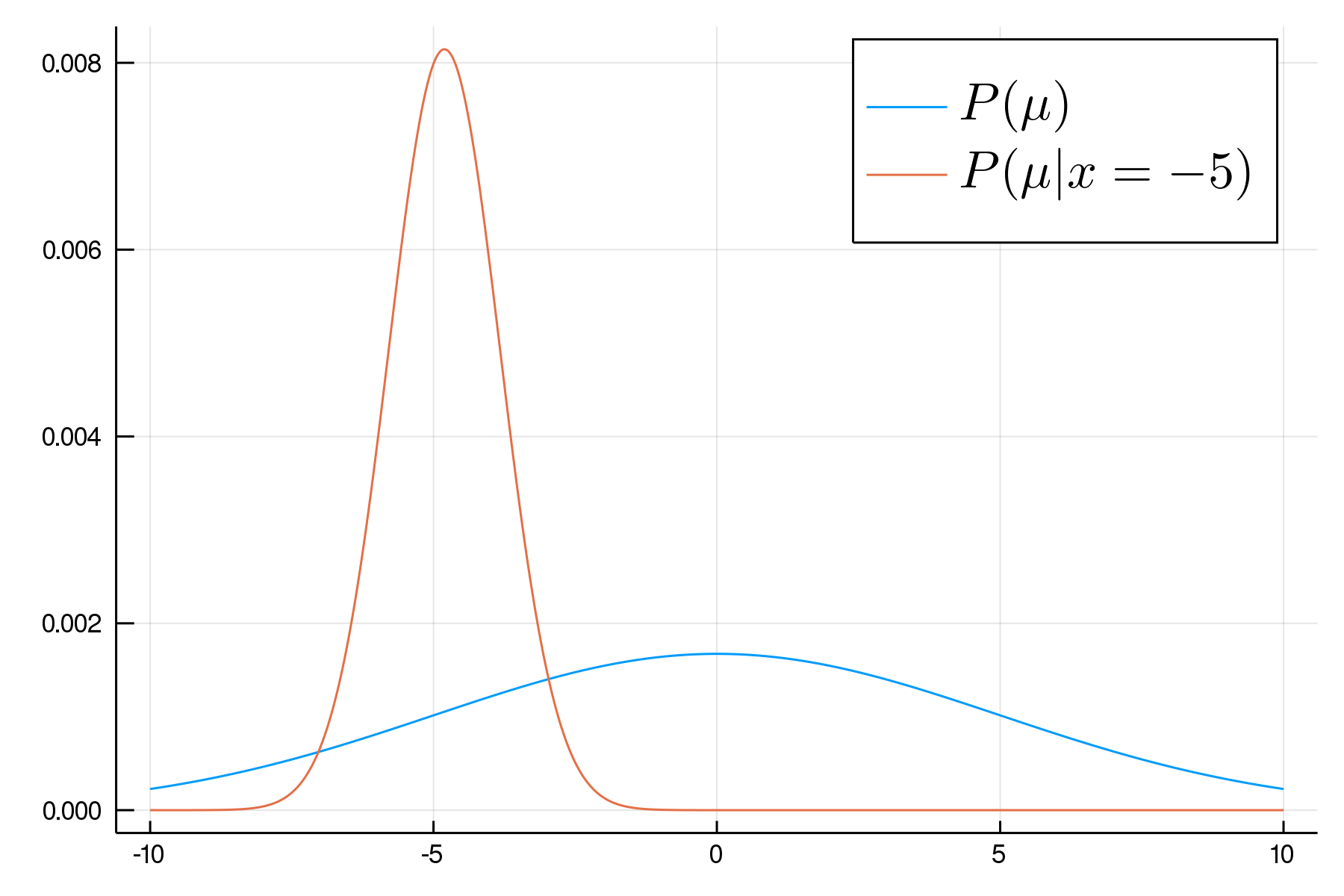
P(\mu,\sigma|x)\propto P(\mu,\sigma)P(x|\mu,\sigma)
\begin{aligned}
\mu &\sim \text{Normal}(0,5)\\
\sigma &\sim \text{Cauchy}_+(0,3) \\
x_j &\sim \text{Normal}(\mu,\sigma)
\end{aligned}
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endSpecialization in Probabilistic Programming
Stan
Fixed-dim parameter space
Continuous only
Turing.jl
"Universal"
(No constraints)
Soss.jl
Fixed-dim "top-level"
Discrete or continuous
specialization
flexibility
High-Level Approach
Result
Code
Model
Model
Model
- Build a Model
- Transform/compose as needed
- Generate inference code
- Execute
Model
Sampling from the Prior
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endjulia> mPrior = prior(m)
@model begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
endjulia> rand(mPrior,2)
(μ = 0.19303947773266164, σ = 2.225230593627689)
(μ = 1.2551251761042306, σ = 16.511128478239772)julia> sourceRand(mPrior)
:(function ##rand#498(args...; kwargs...)
@unpack () = kwargs
μ = rand(Normal(0, 5))
σ = rand(HalfCauchy(3))
(μ = μ, σ = σ)
end)Inline Conditioning
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endjulia> rand(m(N=3)) |> pairs
pairs(::NamedTuple) with 4 entries:
:x => [0.679788, 2.11426, -2.48878]
:σ => 5.83722
:μ => 2.90759
:N => 3julia> m(N=3)
@model x begin
σ ~ HalfCauchy(3)
μ ~ Normal(0, 5)
N = 3
x ~ Normal(μ, σ) |> iid(N)
endInline Conditioning (Expressions)
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endjulia> m(μ = :(σ^2))
@model x begin
σ ~ HalfCauchy(3)
μ = σ ^ 2
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endPreserve topological ordering!
Sampling Particles
julia> particles(m(N=3)) |> pairs
pairs(::NamedTuple) with 4 entries:
:x => Particles{Float64,1000}[3.71 ± 96.0, 2.64 ± 52.0, 2.84 ± 91.0]
:σ => 14.6 ± 100.0
:μ => -0.0188 ± 5.0
:N => 3@model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endSampling From the Posterior
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endjulia> nuts(m;x=randn(100)).samples[1:3] |> DataFrame
3×2 DataFrame
│ Row │ μ │ σ │
│ │ Float64 │ Float64 │
├─────┼───────────┼──────────┤
│ 1 │ 0.0821741 │ 0.992214 │
│ 2 │ 0.0678396 │ 1.11118 │
│ 3 │ 0.04623 │ 0.921818 │Composability
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
endjulia> nuts(m; x = randn(10), errDist = TDist(3)).samples[1:3] |> DataFrame
3×2 DataFrame
│ Row │ μ │ σ │
│ │ Float64 │ Float64 │
├─────┼───────────┼─────────┤
│ 1 │ -0.560033 │ 1.41231 │
│ 2 │ -0.110197 │ 1.15388 │
│ 3 │ -0.389493 │ 1.03683 │m2 = @model x,errDist begin
μ ~ Normal(0,5)
σ ~ HalfCauchy()
N = length(x)
xDist = LocationScale(μ,σ,errDist)
x ~ xDist |> iid(N)
endFirst-Class Models
m2 = @model x,errDist begin
μ ~ Normal(0,5)
σ ~ HalfCauchy()
N = length(x)
xDist = LocationScale(μ,σ,errDist)
x ~ xDist |> iid(N)
endjulia> nuts(m; x = randn(10), errDist = tdist, ν=3).samples[1:3] |> DataFrame
3×2 DataFrame
│ Row │ μ │ σ │
│ │ Float64 │ Float64 │
├─────┼───────────┼──────────┤
│ 1 │ -0.645759 │ 2.34656 │
│ 2 │ 0.364718 │ 2.08522 │
│ 3 │ 0.136806 │ 0.971462 │tdist = @model ν begin
w ~ InverseGamma(ν / 2, ν / 2)
x ~ Normal(0, w ^ 2)
return x
endSymbolic Simplification
m = @model x begin
μ ~ Normal(0, 5)
σ ~ HalfCauchy(3)
N = length(x)
x ~ Normal(μ, σ) |> iid(N)
end
julia> symlogpdf(m) - \frac{μ^{2}}{50} - \log{\left(\frac{\left|{σ}\right|^{2}}{9} + 1 \right)} - \log{\left(5 \right)} - 1.4 - \log{\left(3 \right)}\\
- N \log{\left(σ \right)} - 0.92 N - \frac{1}{2 σ^{2}} \sum_{j=1}^{N} \left( {x}_j - μ \right)^{2}
Symbolic Simplification
julia> f = codegen(m(N=100))
:(function logdensity683(pars)
@unpack (σ, μ, x) = pars
add642 = 0.0
add642 += -1.3705212384941277
add642 += begin
mul643 = 1.0
mul643 *= -1
mul643 *= begin
arg1645 = 3
symfunc644 = (log)(arg1645)
symfunc644
end
mul643
end
add642 += begin
mul646 = 1.0
mul646 *= -1
mul646 *= begin
arg1648 = 5
symfunc647 = (log)(arg1648)
symfunc647
end
mul646
end
add642 += begin
mul649 = 1.0
mul649 *= -1
mul649 *= begin
arg1651 = begin
add652 = 0.0
add652 += 1
add652 += begin
mul653 = 1.0
mul653 *= 1//9
mul653 *= begin
arg1655 = begin
arg1658 = σ
symfunc657 = (abs)(arg1658)
symfunc657
end
arg2656 = 2
symfunc654 = arg1655 ^ arg2656
symfunc654
end
mul653
end
add652
end
symfunc650 = (log)(arg1651)
symfunc650
end
mul649
end
add642 += begin
mul659 = 1.0
mul659 *= -1//50
mul659 *= begin
arg1661 = μ
arg2662 = 2
symfunc660 = arg1661 ^ arg2662
symfunc660
end
mul659
end
add642 += begin
mul663 = 1.0
mul663 *= -0.9189385332046728
mul663 *= N
mul663
end
add642 += begin
mul664 = 1.0
mul664 *= -1
mul664 *= N
mul664 *= begin
arg1666 = σ
symfunc665 = (log)(arg1666)
symfunc665
end
mul664
end
add642 += begin
mul667 = 1.0
mul667 *= -1//2
mul667 *= begin
arg1669 = σ
arg2670 = -2
symfunc668 = arg1669 ^ arg2670
symfunc668
end
mul667 *= begin
sum671 = 0.0
lo673 = 1
hi674 = N
@inbounds @simd(for j = lo673:hi674
Δsum672 = begin
arg1676 = begin
add678 = 0.0
add678 += begin
mul679 = 1.0
mul679 *= -1
mul679 *= μ
mul679
end
add678 += begin
arg1681 = x
arg2682 = j
symfunc680 = (getindex)(arg1681, arg2682)
symfunc680
end
add678
end
arg2677 = 2
symfunc675 = arg1676 ^ arg2677
symfunc675
end
sum671 += Δsum672
end)
sum671
end
mul667
end
add642
end)julia> m(N=100)
@model x begin
σ ~ HalfCauchy(3)
μ ~ Normal(0, 5)
N = 100
x ~ Normal(μ, σ) |> iid(N)
endjulia> f = codegen(m(N=100))Importance Sampling
p = @model begin
α ~ Normal(1,1)
β ~ Normal(α^2,1)
end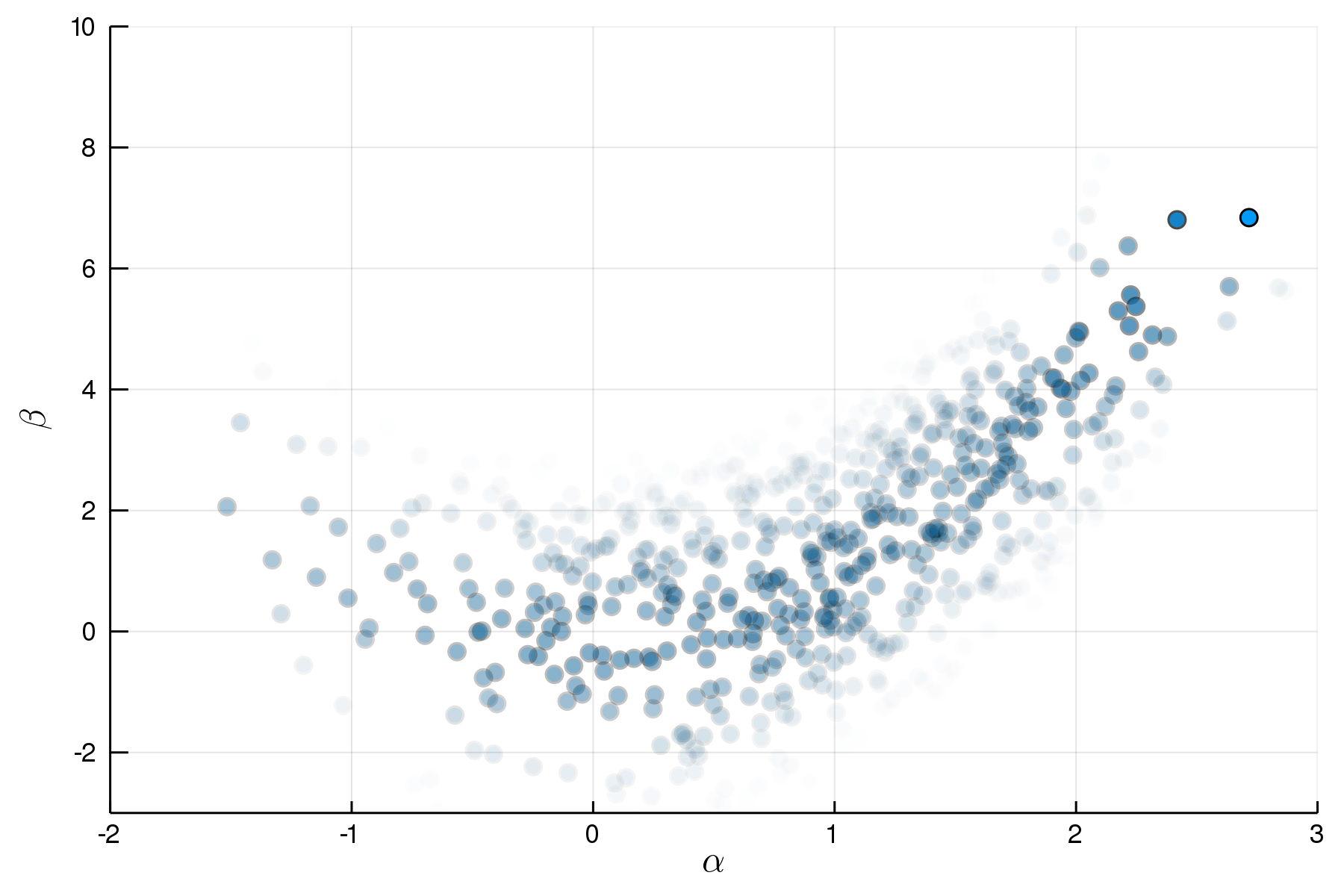
q = @model μα,σα,μβ,σβ begin
α ~ Normal(μα,σα)
β ~ Normal(μβ,σβ)
end julia> sourceParticleImportance(p,q)
:(function ##particlemportance#737(##N#736, pars)
@unpack (μα, σα, μβ, σβ) = pars
ℓ = 0.0 * Particles(##N#736, Uniform())
α = Particles(##N#736, Normal(μα, σα))
ℓ -= logpdf(Normal(μα, σα), α)
β = Particles(##N#736, Normal(μβ, σβ))
ℓ -= logpdf(Normal(μβ, σβ), β)
ℓ += logpdf(Normal(1, 1), α)
ℓ += logpdf(Normal(α ^ 2, 1), β)
return (ℓ, (α = α, β = β))
end)=> Variational Inference
\ell(x) = \log p(x) - \log q(x)
\text{Sample } x \sim q\text{, then evaluate}
In the Works
- Constant-space streaming models (particle or Kalman filter)
- Reparameterizations ("noncentering", etc)
- Deep learning via Flux
-
"Simulation" constructor
-
Turing.jl interop
Thank You!

Special Thanks for
What's in a Model?
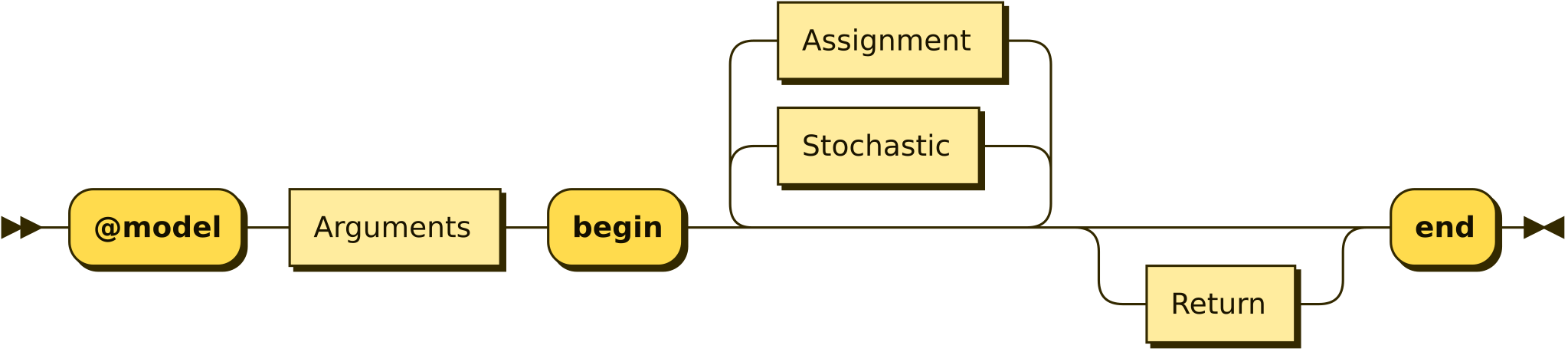
Railroad diagrams designed using https://www.bottlecaps.de/rr/ui
Argmuments
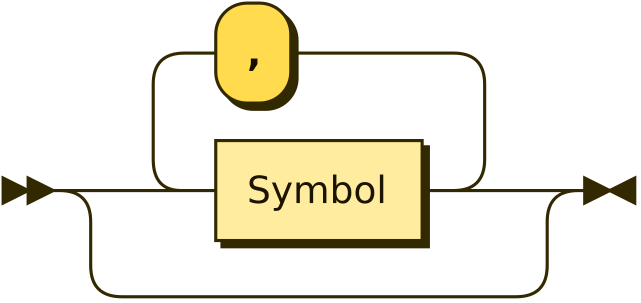

Assignment


Stochastic
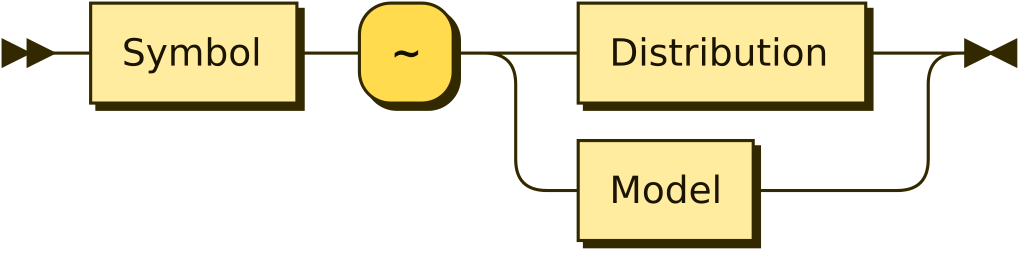

Return


2019-07-25 JuliaCon
By Chad Scherrer
2019-07-25 JuliaCon
- 1,801



