Digital Curvature Flow
Daniel Martins Antunes
Université Savoie Mont Blanc, LAMA
IHP Winter School: The Mathematics of Imaging.
January 7, 2019
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
How to use geometric information in image processing tasks?
Perimeter
Tangent
Curvature
geometric information
image
processing tasks
Segmentation
Denoising
Stereo
Perimeter
Tangent
Denoising
Stereo
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
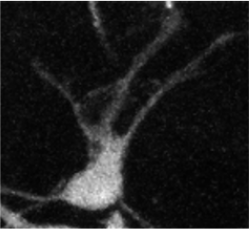



Prior information of object geometry
Data term
Data + Perimeter term
Data + Curvature term
[El-Zehiry, 2010]
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
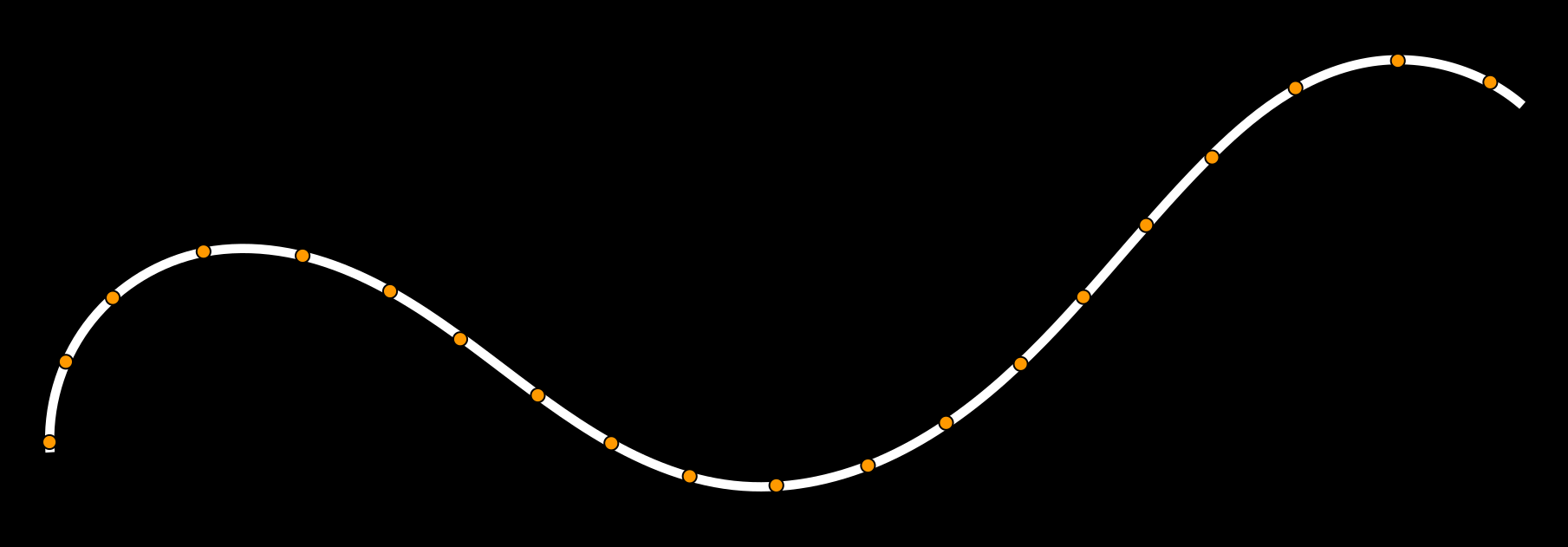
State-of-Art limitations
Curvature discretizations are not suited for digital data
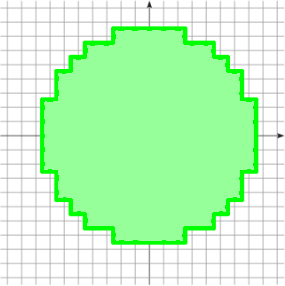
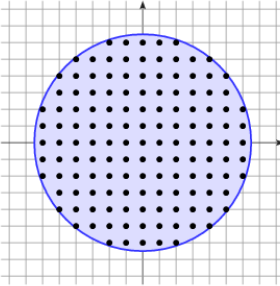
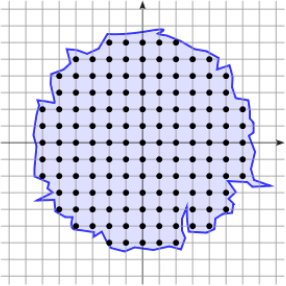
[Roussillon, 2011]
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
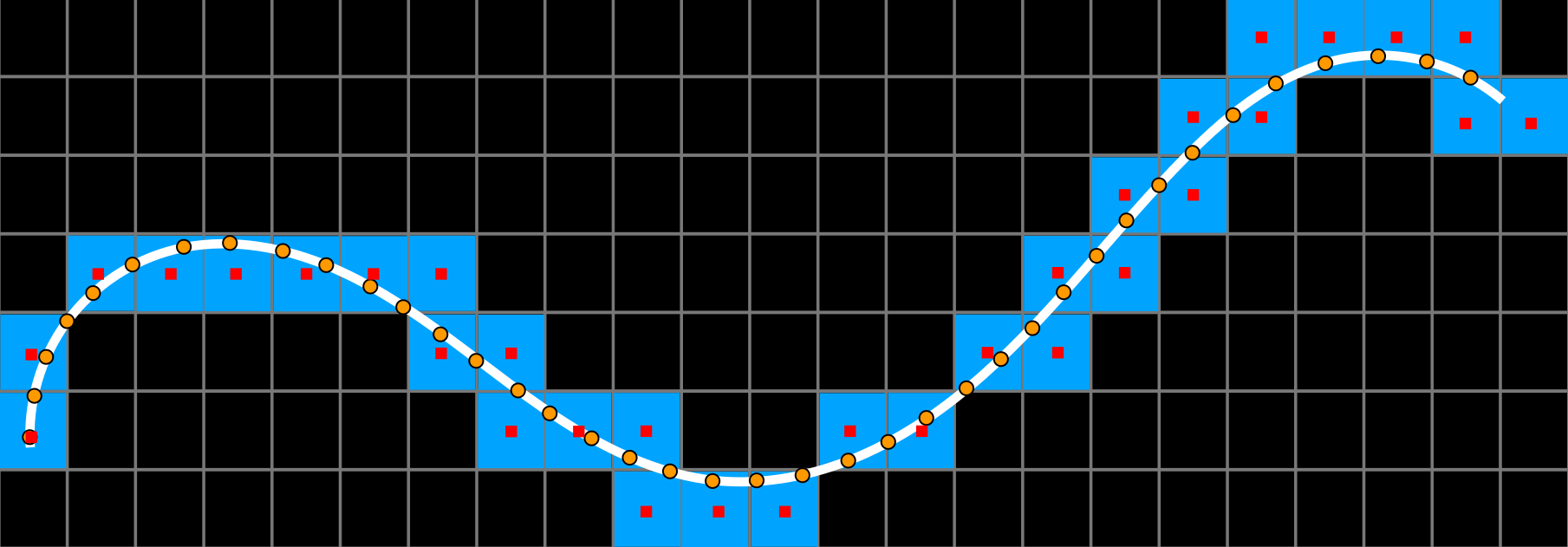
State-of-Art limitations
Curvature discretizations are not suited for digital data





Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
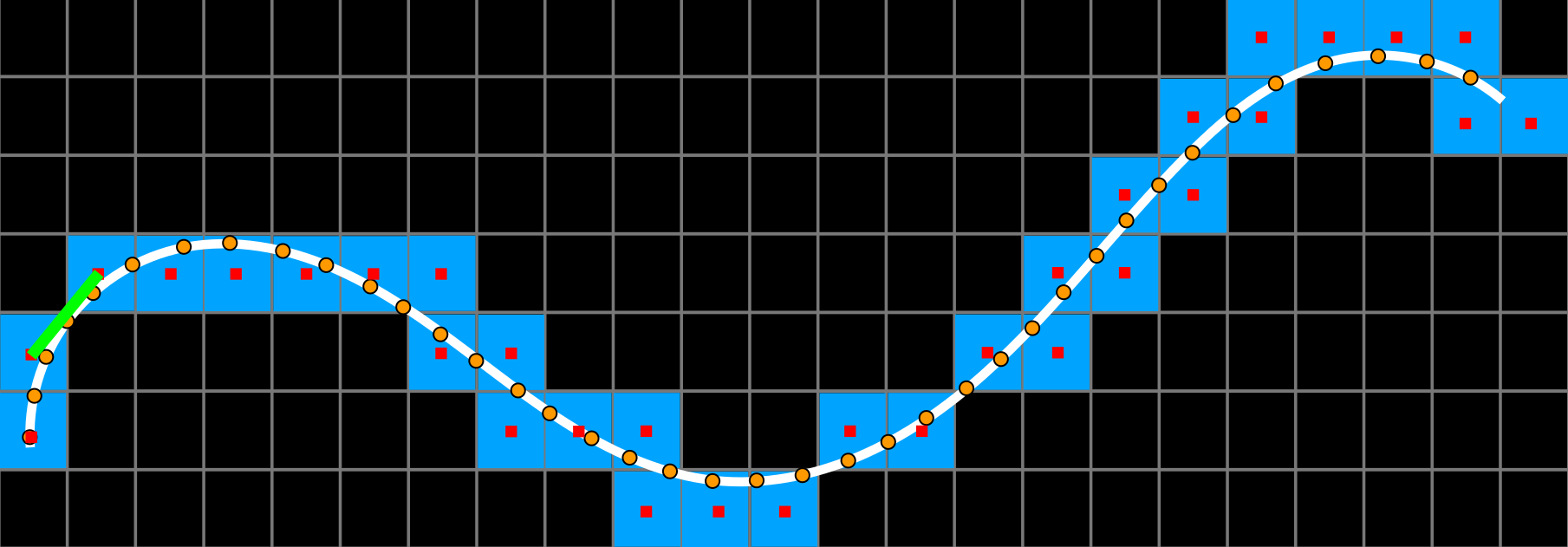
Multigrid convergent estimators
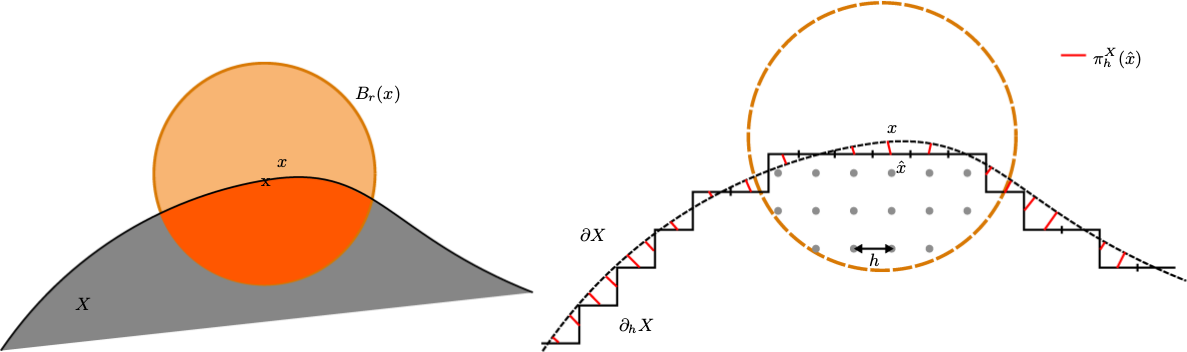
[Coeurjolly, 2013]
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Multigrid convergent estimators

[Coeurjolly, 2013]
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Shape Evolution

Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Shape Evolution

Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Shape Evolution

Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Shape Evolution
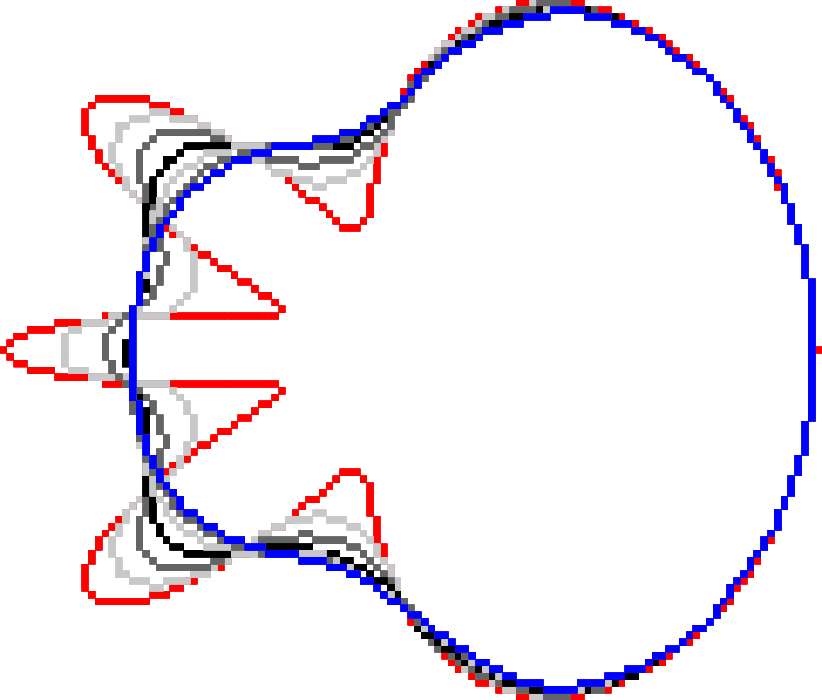
Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Image Segmentation

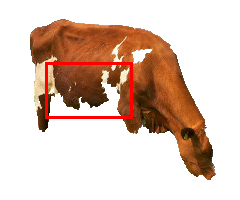



Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Image Segmentation





Digital Curvature Flow
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Motivation
State-of-Art
Contribution
Conclusion
Multigrid convergent estimator and optimization framework;
Positive Aspects
Evolution model regularizes with respect to curvature.
Drawbacks
Too local. The model is uncapable to complete regions.
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Digital Curvature Flow
Thank you for your attention!
Daniel Martins Antunes
IHP Winter School: The Mathematics of Imaging. January 7, 2019
Digital Curvature Flow
[El-Zehiry, 2010] N. Y. El-Zehiry and L. Grady. Fast global
optimization of curvature.
[Roussilon, 2011] T. Roussillon and J.-O. Lachaud. Accurate
curvature estimation along digital contours
with maximal digital circular arcs.
References
[Coeurjolly, 2013] D. Coeurjolly, J.-O. Lachaud, and J. Levallois.
Integral based curvature estimators in digital
geometry.
Digital Curvature Flow (Flash)
By Daniel Martins Antunes
Digital Curvature Flow (Flash)
5 minutes flash presentation of the motivation and results of the digital curvature flow presented during the winter school: Mathematics of Imaging at CIRM in Marseille.
- 260



