Digital Curvature Evolution Model for Image Segmentation
Daniel Antunes
Discrete Geometry for Computery Imagery
ESIEE Paris. March 27, 2019
Université Savoie Mont Blanc, LAMA
Hugues Talbot
CentraleSupélec Université Paris-Saclay
Jacques-Olivier Lachaud
Presentation plan
Introduction
Motivation problems
Regularization in imaging
Curvature as regularization
Discretization and multigrid convergence
Contribution
Curve Evolution Model
Interpretation
Discussion and application
Conclusion
Digital Curvature Evolution Model for Image Segmentation
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Introduction
Contribution
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Image segmentation
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Conclusion
[Unger, Werlberger, 2011]
Denoising
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
[Furukawa, Hernández 2015]
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
3D Reconstruction
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Segmentation
Denoising
3D Reconstruction
Inverse Problems
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
\displaystyle u^\star = \text{arg} \min_{u \in \Omega} E(u)
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Solving Strategy
Model for denoising
\displaystyle E(u) = \alpha || g - u ||^2 +
Let be the image space
where is the noisy (input) image.
\Omega
g
Solution resemble input image
Solution should be smooth
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
\beta || \nabla u ||^2,
\displaystyle E(u,K) = \int_{\Omega - K}{ (g-u)^2 dx} + \lambda\int_{\Omega - K}{||\nabla u||^2 dx} + \int_{K}{dx}
Mumford-Shah model
Similar to original image
Piecewise smooth
Small perimeter
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Image segmentation
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Binary piece-wise smooth [Chan; Vese, 2001]
Optimization of Ambrosio Tortorelli energy [Foare; Lachaud; Talbot, 2016]
Data term
Data + Perimeter term
Data + Curvature term
[El-Zehiry, 2010]
Curvature as regularization in segmentation
Completion property
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
\displaystyle E(u) = \int_{\Omega}{ ( u - g )^2 dx } + \int_{\partial u}{ \alpha + \beta \kappa^2 ds}
Non-convex term
Difficult to optimize
Second order term. Should be careful with discretization scheme
Integration domain is unknown
\Big\{
Elastica energy
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Curvature as regularization in segmentation
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
\hat{\kappa}(x_i)=\frac{\alpha_i}{\min\{l_i,l_{i+1}\}}
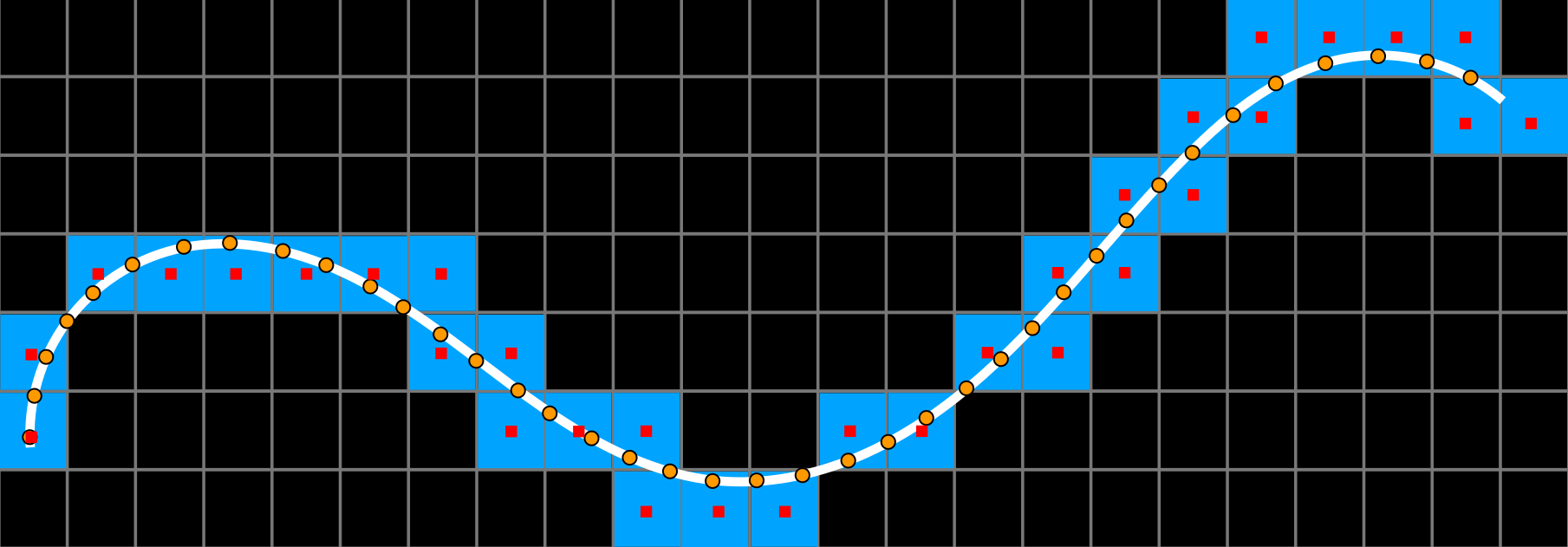
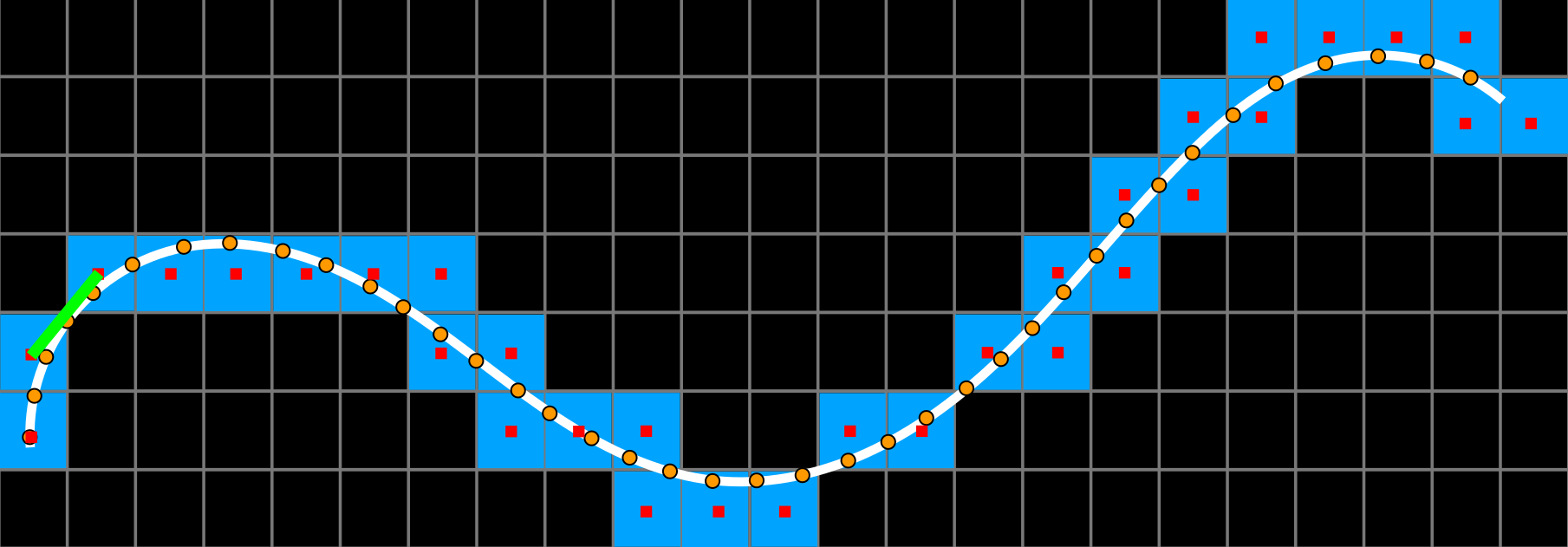
Curvature discretization
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
x_i
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
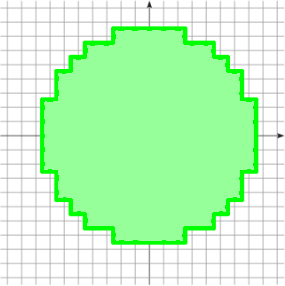
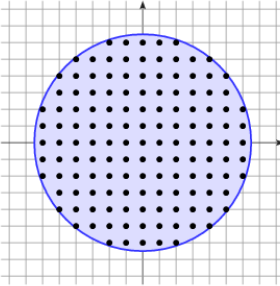
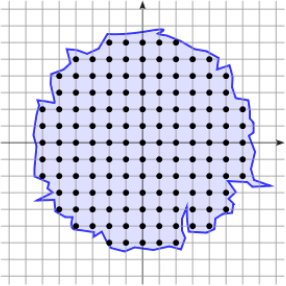
[Roussillon, Lachaud 2011]
Digitization ambiguity
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Multigrid Convergence
\forall \hat{x} \in \partial_hX \text{ with } || \hat{x} - x ||_{\infty} \leq h\\
|| \hat{E}(D_h(X),\hat{x},h) - E(X,x)|| \leq \tau_{X}(h)
\exists h_X > 0 \text{ such that, for any } 0 < h < h_X \text{ and } x \in \partial X
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
E(X,x)
\hat{E}(D_h(X),\hat{x},h)
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
The estimated quantity gets arbitrarily close from as resolution increases.
Integral based estimator for curvature
\hat{\kappa}_{R,h}(x_i) = \frac{3}{R^3} \Big( \frac{\pi R^2}{2} - \widehat{Area} ( B_{R,h}(x_i) \cap D_h ) \Big)
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
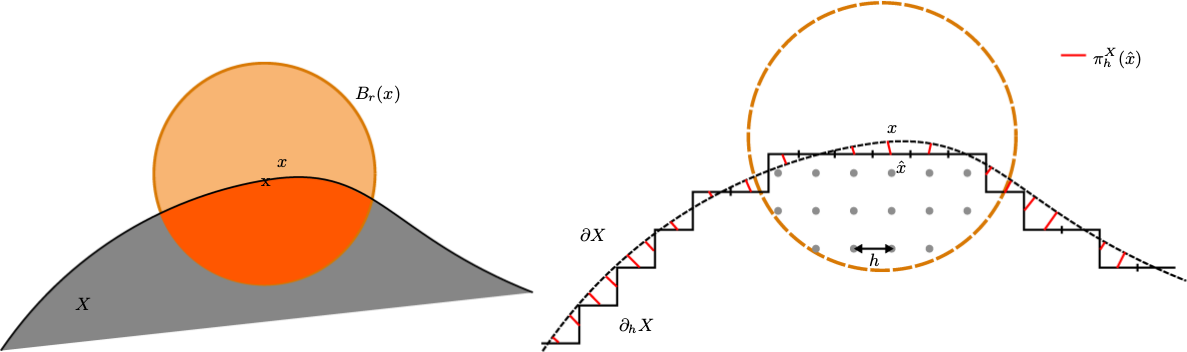
[Coeurjolly, Lachaud, Levallois 2013]
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
To sum up
We want to use curvature as regularization term in models of image processing tasks
We believe that by using a multigrid convergent estimator, we can recover better results
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Notation
Introduction
Contribution
Conclusion
Let be a connected digital shape
D
\mathcal{C}(D)
4-connected pixel boundary
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Digital Curvature Evolution Model for Image Segmentation
Introduction
Contribution
Conclusion
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Cells (pixels)
Linels
Pointels
Cellular grid model
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Curve evolution model
\displaystyle E(u) = \int_{\partial u}{ \kappa^2 ds}
\displaystyle \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Digital Curvature Evolution Model for Image Segmentation
Introduction
Contribution
Conclusion
Curve evolution model
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Digital Curvature Evolution Model for Image Segmentation
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}, \quad y \in \{0,1\}^{|\mathcal{C}(D)|}
Introduction
Contribution
Conclusion
A first evolution
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Sensible regions indication
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
\displaystyle \min_{y} \alpha \sum_{y_i \in \mathcal{O}}{\hat{k}_R^2(y_i)} + \beta \sum_{y_i \in \mathcal{O}}\sum_{y_j \in \mathcal{N}_4(y_i)}{ (y_i-y_j)^2}
\displaystyle \min_{y} \sum_{y_i \in \mathcal{O}}{\hat{k}_R^2(y_i)}
\alpha=1\\
\beta=0.5
\alpha=1\\
\beta=1.0
\alpha=1\\
\beta=2.0
Introduction
Contribution
Conclusion
Perimeter penalization
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Optimization region
\mathcal{O}
Computation Region
Introduction
Contribution
Conclusion
Filtering artifacts
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
\displaystyle \min_{y} \sum_{a_i \in \mathcal{A}(D)}{\hat{k}_R^2(a_i,y)}, \quad y \in \{0,1\}^{|\mathcal{C}(D)|}
\mathcal{A}
Introduction
Contribution
Conclusion
Bands evolution
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Bands evolution
Introduction
Contribution
Conclusion
Ball radius effect
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
R=3
R=5
Introduction
Contribution
Conclusion
Ball radius effect
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
R=5
R=7
\displaystyle \min_{y} \sum_{p \in \mathcal{C}(D)}{ \left( (1/2+ |F_r(p)|-c_2) \cdot \sum_{y_i \in Y_r(p)}{y_i} + \sum_{ y_i,y_j \in Y_r(p); i < j }{y_iy_j} \right) }
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}
Supermodular energy
Introduction
Contribution
Conclusion
\frac{ \partial^2\hat{E} }{\partial y_i \partial y_j} \geq 0, \quad \forall i \neq j
Quadratic pseudo-boolean function
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Quadratic pseudo-boolean function
QPBOP: Returns partial solution. Some pixels are not labeled.
QPBOI: Improves a partial solution value and returns a full labeling. Partial optimality property is loss.
If energy is submodular, QPBOP labels all variables.
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Unlabeled pixels
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Segmentation post-processing
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Introduction
Contribution
Conclusion
Segmentation post-processing
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
1. Curve Evolution Model
2. Interpretation
3. Applications and discussion
Model summary
Flow based on a multigrid convergent estimator of curvature
Post-processing step in image segmentation
Works well with extra terms ( data fidelity, perimeter )
Too local. Completion property is not recovered
Introduction
Contribution
Conclusion
Discrete Geometry for Computery Imagery
ESIEE, Paris. March 27, 2019
Digital Curvature Evolution Model for Image Segmentation
Thank you for your attention!
Digital Curvature Evolution Model for Image Segmentation
Daniel Antunes
Université Savoie Mont Blanc, LAMA
Hugues Talbot
CentraleSupélec Université Paris-Saclay
Jacques-Olivier Lachaud
Digital Curvature Evolution Model for Image Segmentation
By Daniel Martins Antunes
Digital Curvature Evolution Model for Image Segmentation
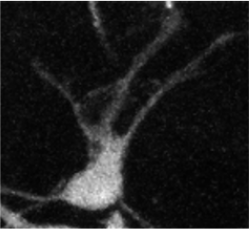
Recent works have indicated the potential of using curvature as a regularizer in image segmentation, in particular for the class of thin and elongated objects. These are ubiquitous in biomedical imaging (e.g. vascular networks), in which length regularization can sometime perform badly, as well as in texture identification. However, curvature is a second-order differential measure, and so its estimators are sensitive to noise. State-of-art techniques make use of a coarse approximation of curvature that limits practical applications. We argue that curvature must instead be computed using a multigrid convergent estimator, and we propose in this paper a new digital curvature flow which mimics continuous curvature flow. We illustrate its potential as a post-processing step to a variational segmentation framework.
