MATH202 TP #3
Compression avec perte
Objectifs
- Comparer les différentes méthodes de codage/compression;
- Discerner quand utiliser la compression avec pertes:
-
Réduction de dimensions;
-
Découvrir la transformée de Fourier discrète.
Le TP doit être fait en binôme.
Codeur: Responsable pour l'implementation.
Navigateur: Responsable pour veiller à la qualité du code (?)
Organisation
Sprint 1
Sprint 2
Sprint 3
10
60
110
120
170
180
0
40min
10min
On bosse
On discute
Le binôme doit alterner les rôles de codeur et de navigateur à chaque sprint
Encodage
Transformer
une message M dans
une message codée M'
Description
Réduction de symboles/transmission
Buts
Compression
Cryptographie
- Taille fixe:
- ASCII.
-
Taille variable:
-
UTF-8;
-
-
Taille dynamique
-
Code Huffman.
-
Caracteristique clé
non-ambiguïté
Code Préfixe
LZ78
Code par dictionnaire
Le code d'un symbole peu fréquent a la même taille que le code d'un symbole très fréquent.
Le code de symboles plus fréquents ont une taille plus petites que ceux moins fréquents. Le dictionnaire est variable par chaque message
On accorde les symboles le plus souvent utilisés et on crée un dictionnaire (fixe) que assigne un code plus petite aux symboles les plus fréquents.
Comparaison compression
C'est pas l'homme qui prend la mer
C'est la mer qui prend l'homme.
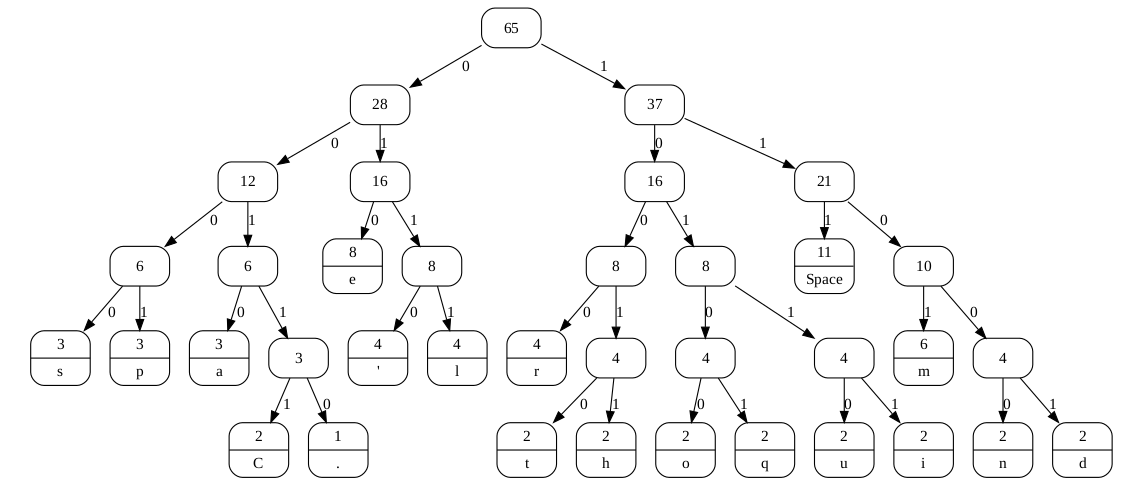
Huffman
267 bits
LZ78
608 bits
Strophe
Chanson
2x Chanson
10x Chanson
17696 bits
32080 bits
113136 bits
11713 bits
23426 bits
117130 bits
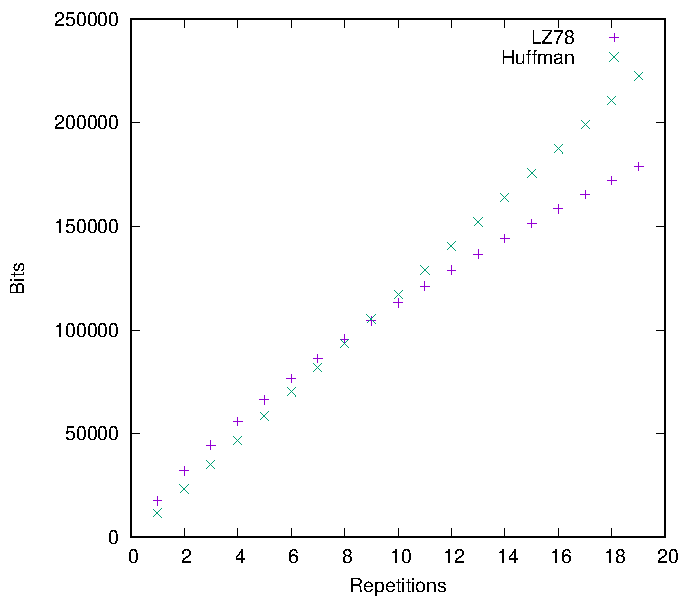
Dès que le vent soufflera, Renaud
Code Huffman x LZ78
As for me, I am tormented with an everlasting itch for things remote. I love to sail forbidden seas, and land on barbarous coasts.
Moby-Dick; or, The Whale, Herman Melville
Huffman
LZ78
5961040 bits
5589354 bits
LZ78/Huffman = 1.07
Comparaison compression
Code Huffman x LZ78
ta_tata_tati
a_tata_tatit
_tata_tatita
tata_tatita_
ata_tatita_t
ta_tatita_ta
a_tatita_tat
_tatita_tata
tatita_tata_
atita_tata_t
tita_tata_ta
ita_tata_tat
ta_tata_tati
a_tata_tatit
_tata_tatita
tata_tatita_
ata_tatita_t
ta_tatita_ta
a_tatita_tat
_tatita_tata
tatita_tata_
atita_tata_t
tita_tata_ta
ita_tata_tat
9aatttttia__a
1 2 3 4 5 6 7 8 9 101112
Comparaison compression
Transformée de Burrows Wheeler
As for me, I am tormented with an everlasting itch for things remote. I love to sail forbidden seas, and land on barbarous coasts.
Moby-Dick; or, The Whale
Huffman
LZ78
5961040 bits
5589354 bits
LZ78/Huffman = 1.07
5476976 bits
LZ78/Huffman = 0.98
avec BWT
Comparaison compression
Code Huffman x LZ78
Compression avec perte
- On échange un peu d'information pour gagner beaucoup en compression;
- La compression avec perte n'est adapté qu'a certain types de documents
Peu de perte est admissible
Aucune perte est admissible
Image
Audio
Texte
Executable
Quand c'est acceptable?
Compression avec perte
Moyenne par bloc


[10,20,30,20,70,50,20,30,90,60]

[40,40,40,40,40,40,40,40,40,40]
somme: 400
taille du bloc: 10
Sprint #1
Objectifs: Questions 1, 2, 3 et 4
Traverse de listes:
Le dernière élément:
liste[ début : fin : pas ]liste[-1]Initialization de listes:
liste = [0]*5
#[0,0,0,0,0]Somme
sum( [1,2,3] ) #6Ajouter des elements
l=[1,2] + [3,4] # [1,2,3,4]
l.extend( [5,6] ) #[1,2,3,4,5,6]
l.append( 7 ) #[1,2,3,4,5,6,7]s="Taille: {} octets".format(42)
#Taille: 42 octetsFormatation de strings:
Mini-Activité
Quiz
Quiz:
L'arbre de Huffman d'une message M est montrée dans la figure ci-dessous.
C'est quel le symbole plus fréquent?
A) f
B) a
C) e
D) space
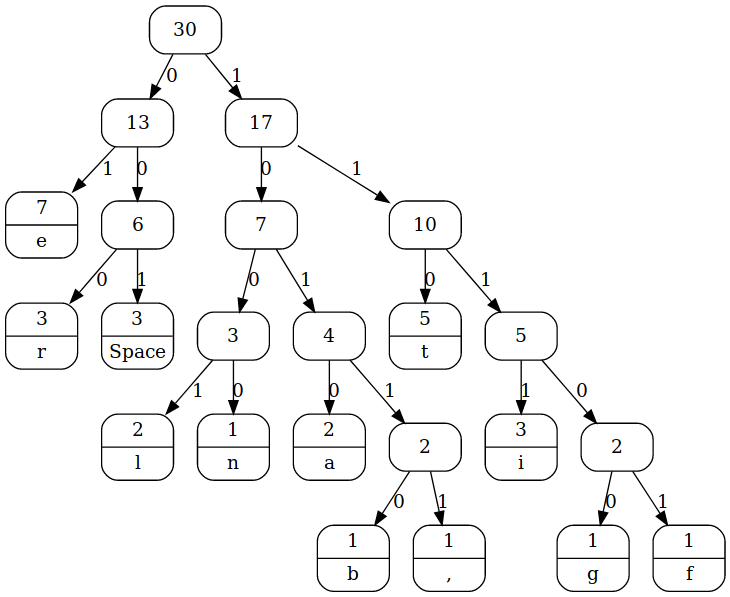
Quiz:
Le resultat d'une compression moyenne par bloc en utilisant un bloc de taille 3 est le suivant
[ 100 100 100 200 200 200 100 100 100 ]
B) [ 200 50 50 300 200 100 300 0 0 ]
C) [ 80 80 140 150 150 300 70 70 160 ]
D) [ 100 100 100 200 200 200 100 100 100 ]
A) Pas possible à dire
C'était quelle l'image original?
Quiz:
Considère les bases B1 et B2 d'un espace bi-dimensionnelle ci-dessous
B1 = { (1,0) ; (0,1) }
B2 = { (-1,2) ; (3,0) }
B) (-2,6)
C) (-2,0)
D) (2,2)
A) (4,4)
Soit v = (2,2) un vecteur dans la base B1. Le point pv que représente ce vecteur dans le plan cartésienne c'est
pv = 2*(1,0) + 2*(0,1) = (2,2)
Soit v un vecteur avec les mêmes coordonnées que v , i.e.,
(2,2), mais dans la base B2. Quelle point représente-t-il?
B1
B1
B1
B2
B1
Quiz:
Considère les bases B1 et B2 d'un espace bi-dimensionnelle ci-dessous
B1 = { (1,0) ; (0,1) }
B2 = { (-1,2) ; (3,0) }
B) (1,1)
C) (-2,1)
D) (1,-2)
A) (2,2)
Soit v = (2,2) un vecteur dans la base B1. Le point pv que représente ce vecteur dans le plan cartésiennes c'est
pv = 2*(1,0) + 2*(0,1) = (2,2)
B1
B1
B1
B2
B1
Quelles sont les coordonnées qui doit avoir v tel qu'il représente le même point que v , i.e., pv = (2,2) ?
B2
Compression avec perte


Exemple: Logements sur Airbnb à Paris
- Data disponible sur insideairbnb.com;
- Plusieurs attributs sont quantifiées
- Prix;
- Pieds carré;
- Avis positifs;
- Taux d'occupation;
- ...
- Parfois, il y a des attributs qui sont redondant, or qui peuvent être estimée a partir d'autres.
Réduction de dimension
Compression avec perte

Exemple: Logements sur Airbnb à Paris
- Normalement, on a besoin de trois quantités pour représenter un valeur 3D;
- Cependant, on peut constater visuellement que l'ensemble peut être bien estimée par un plan;
- Si on assume l'erreur d'estimation, on peut utiliser deux valeurs au lieu de trois pour représenter chaque point de l'ensemble.
Réduction de dimension
Compression avec perte

Réduction de dimension
Exemple: Logements sur Airbnb à Paris
- Dans la langage de l’algèbre linéaire, on avait fait deux choses:
- Changement de base: Au lieu du vecteurs canoniques (1,0,0); (0,1,0); (0,0,1) on utilise les vecteurs u,v,w, où u et v sont vecteurs dans le plan jaune et w c'est son vecteur normale, i.e., w = u x v.
- On abandonne le vecteur w, et on utilise seulement u et v pour représenter l'ensemble de données.
Compression avec perte
Réduction de dimension
Exemple: Images
- Dans les images il y a aussi de redondance et de valeurs qui peuvent être estimée a partir de autres;
- Néanmoins, les images sont exemples de objets multidimensionnelles (chaque pixel c'est une dimension) et trouver la meilleur base c'est pas un problème triviale;
- Mais il y a des bases "standard" qui sont bien adaptés pour la représentation d'images et aussi de son digitales, comme par exemple, cela donnée par la Transformée de Fourier Discrète.
Compression avec perte
Transformée de Fourier Discrète
La base TFD pour une space de 100 dimensions (e.g. image 10x10)
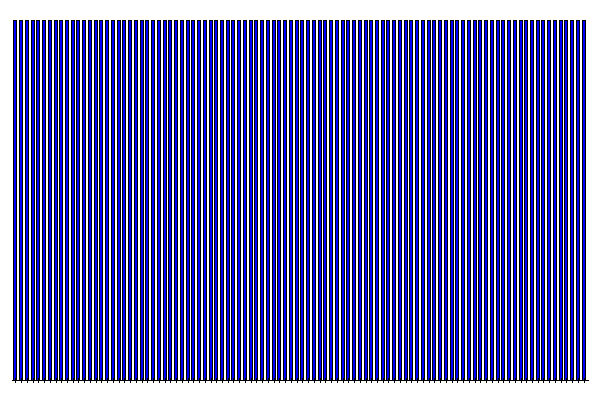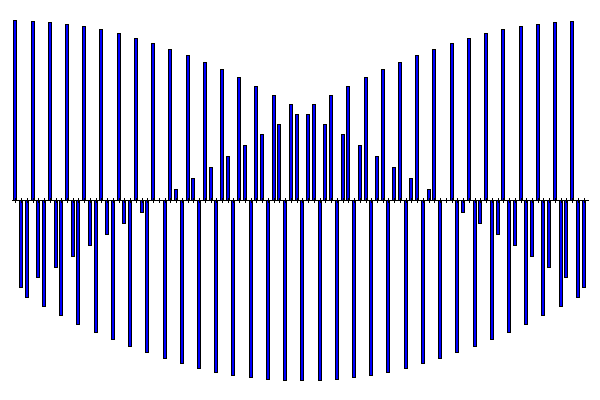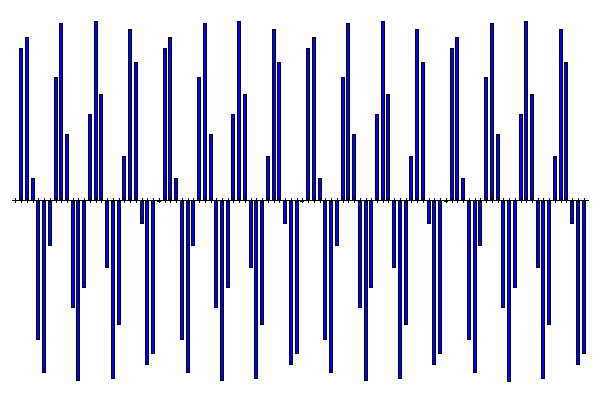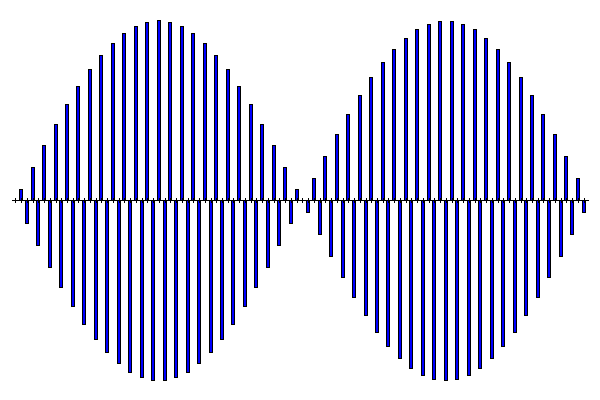
Sprint #2
Objectifs: Questions 5, 6, 7 et 8
Enumerate
enumerate( ["a","b","c"] )
#[ (0,"a"), (1,"b"), (2,"c") ]Zip
zip( [0,2,4], [1,3,5] )
#[ (0,1), (2,3), (4,5) ]Initialisation par expression
l=[ round(x/3) for x in range(0,10) ]
#[0,0,1,1,1,2,2,2,3,3]Mini-Activité
Quiz
Quiz:
Considère les points en 4 dimensions ci-dessous:
(1,1,1,1); (2,2,2,2); (3,3,3,3); (4,4,4,4); (5,5,5,5)
B) Deux dimensions
C) Trois dimensions
D) Pas possible de réduire la dimension
A) Une dimension
On peut representer le même ensemble en utilisant
Quiz:
Normalement, combien de valeurs on doit garder pour représenter les 15 points noirs dans la figure ci-dessous?
B) 30
C) 2
D) 45
A) 15
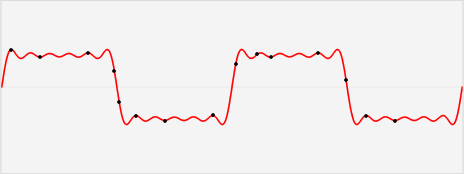
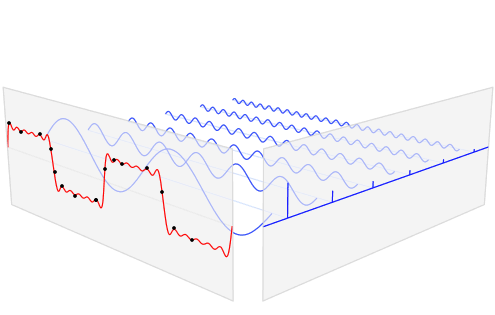
Quiz:
Si on sait que la courbe rouge peut être ecrit comme
F(x) = Ai*sin(bix), 1 <= i <= 6,
les valeurs Ai, bi donnés. Ça veut dire que chaque point pi peut être écrit comme
pi = ( ci,F(ci) ).
Combien de valeurs on doit garder pour représenter les mêmes 15 points?
B) 30
C) 6
D) 90
A) 15
Sprint #3
Objectifs: Questions 9, 10, 11 et 12
Mini-Activité
Peer Review (?)
Eigenfaces
Application de réduction de dimension a reconnaissance facial
Faces qu'on veut reconnaître
(peut être des milliers)


K vecteurs le plus représentatif de l'ensemble
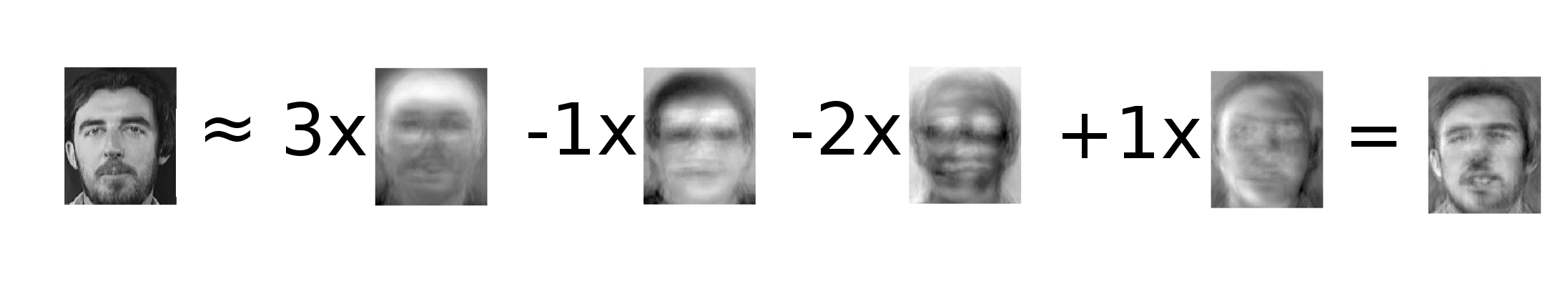
Références
Math202 - TP3
By Daniel Martins Antunes
Math202 - TP3
Compression avec perte
- 347



