Digital Curvature Flow
Daniel Martins Antunes
Université Savoie Mont Blanc, LAMA
Seminar LIMD
March 21, 2019
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Presentation plan
Introduction
Motivation problems
Regularization in imaging
Curvature as regularization
Discretization and multigrid convergence
Contribution
Optimization model
Non-submodular energies
Interpretation
Discussion and application
Conclusion
Digital Curvature Flow
Introduction
Contribution
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Image segmentation
[Antunes, 2019]
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Conclusion
Digital Curvature Flow
[Unger, 2011]
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Denoising
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
[Furukawa, 2015]
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
3D Reconstruction
Introduction
Contribution
Conclusion
Digital Curvature Flow
Segmentation
Denoising
3D Reconstruction
Inverse Problems
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
u⋆=argu∈ΩminE(u)
\displaystyle u^\star = \text{arg} \min_{u \in \Omega} E(u)
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Solving Strategy
Model for denoising
E(u)=α∣∣g−u∣∣2+β∣∣∇u∣∣2,
\displaystyle E(u) = \alpha || g - u ||^2 + \beta || \nabla u ||^2,
Let be the image space
where is the noisy (input) image.
Ω
\Omega
g
g
Solution resemble input image
Solution should be smooth
Introduction
Contribution
Conclusion
Digital Curvature Flow
Denoising: Bayesian interpretation
The noise is modeled as a gaussian (μ=0; σ=1)
Input image
Perfect image
Noise
Pr(u∣g)=Pr(g)Pr(g∣u)Pr(u)
Pr(u|g) = \frac{ Pr(g|u)Pr(u) }{ Pr(g) }
Pr(g∣u)=(2π) e(−∣∣g−u∣∣2/2)
Pr(g|u) = \frac{e^{(- ||g-u||^2/2 )}}{\sqrt(2\pi) }
Pr(u)=e−R(u)
Pr(u) = e^{-R(u)}
u⋆=argumin2∣∣g−u∣∣2+R(u)
\displaystyle u^\star = \text{arg} \min_{u} \quad \frac{|| g - u ||^2}{2} + R(u)
Regularization term
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
g=u+η
g = u + \eta
Introduction
Contribution
Conclusion
Digital Curvature Flow
Regularization terms
Tikhonov
R(u)=∫Ω∣∇u(x)∣2dx
R(u)= \int_{\Omega}{ |\nabla u(x)|^2 dx }
R(u)=∫Ω∣∇u(x)∣dx
R(u)= \int_{\Omega}{ |\nabla u(x)|dx }
Total Variation
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
E(u,K)=∫Ω−K(g−u)2dx+λ∫Ω−K∣∣∇u∣∣2dx+∫Kdx
\displaystyle E(u,K) = \int_{\Omega - K}{ (g-u)^2 dx} + \lambda\int_{\Omega - K}{||\nabla u||^2 dx} + \int_{K}{dx}
Mumford-Shah model
Similar to original image
Piecewise smooth
Small perimeter
Chan-Vese
Ambrosio-Tortorelli (DC formulation by Foare)
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Image segmentation
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
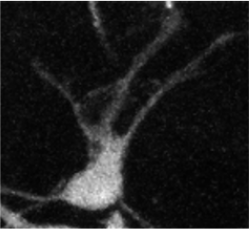
Data term
Data + Perimeter term
Data + Curvature term
[El-Zehiry, 2010]
Curvature as regularization in segmentation
Completion property
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
E(u)=∫Ω(u−g)2dx+∫∂uα+βκ2ds
\displaystyle E(u) = \int_{\Omega}{ ( u - g )^2 dx } + \int_{\partial u}{ \alpha + \beta \kappa^2 ds}
Non-convex term
Difficult to optimize
Second order term. Should be careful with discretization scheme
Integration domain is unknown
{
\Big\{
Elastica energy
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Curvature as regularization in segmentation
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
κ^(xi)=min{li,li+1}αi
\hat{\kappa}(x_i)=\frac{\alpha_i}{\min\{l_i,l_{i+1}\}}
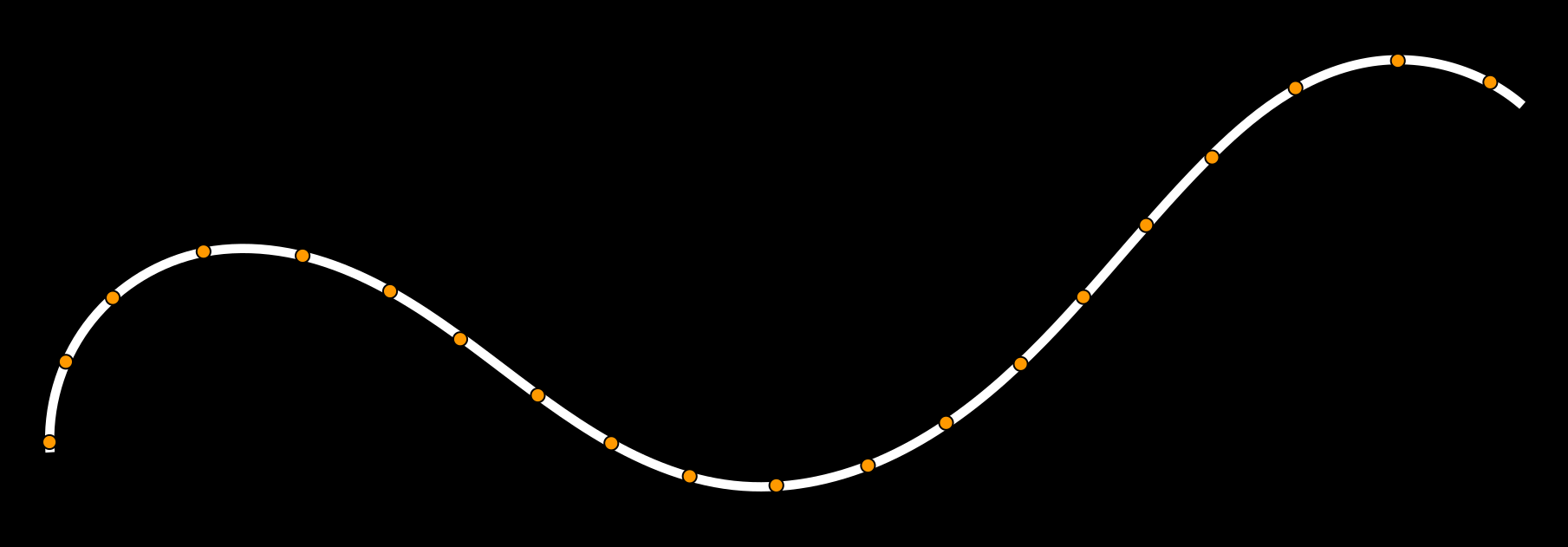
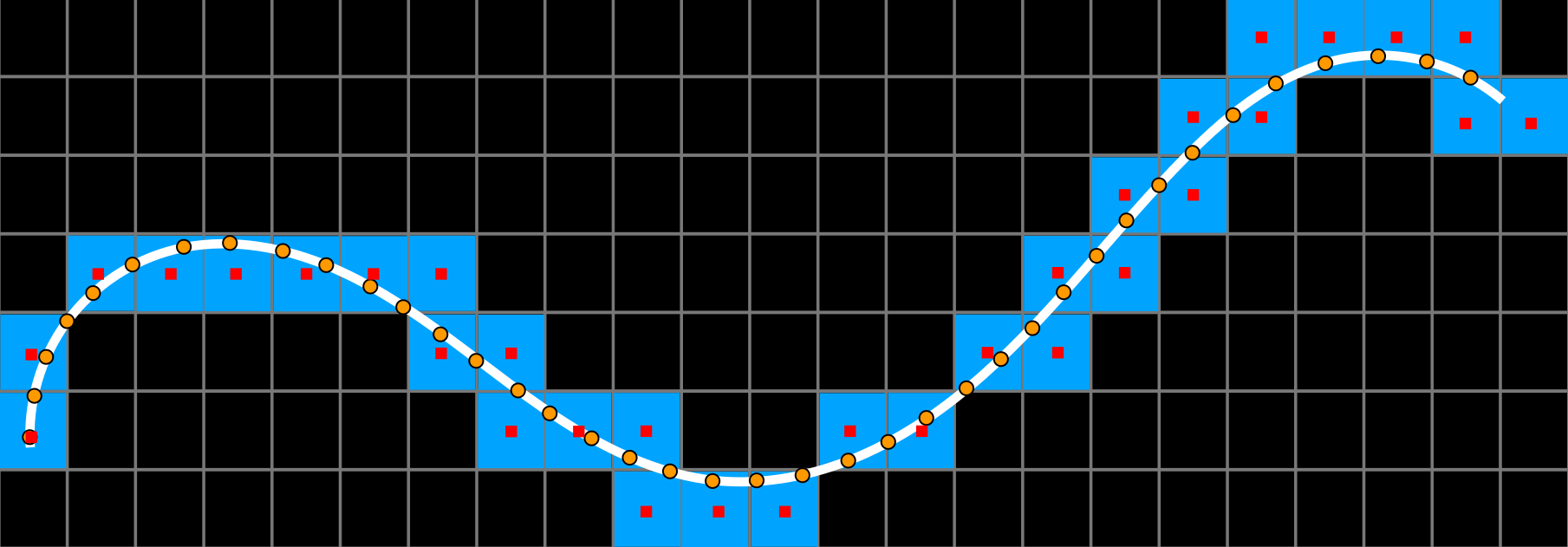
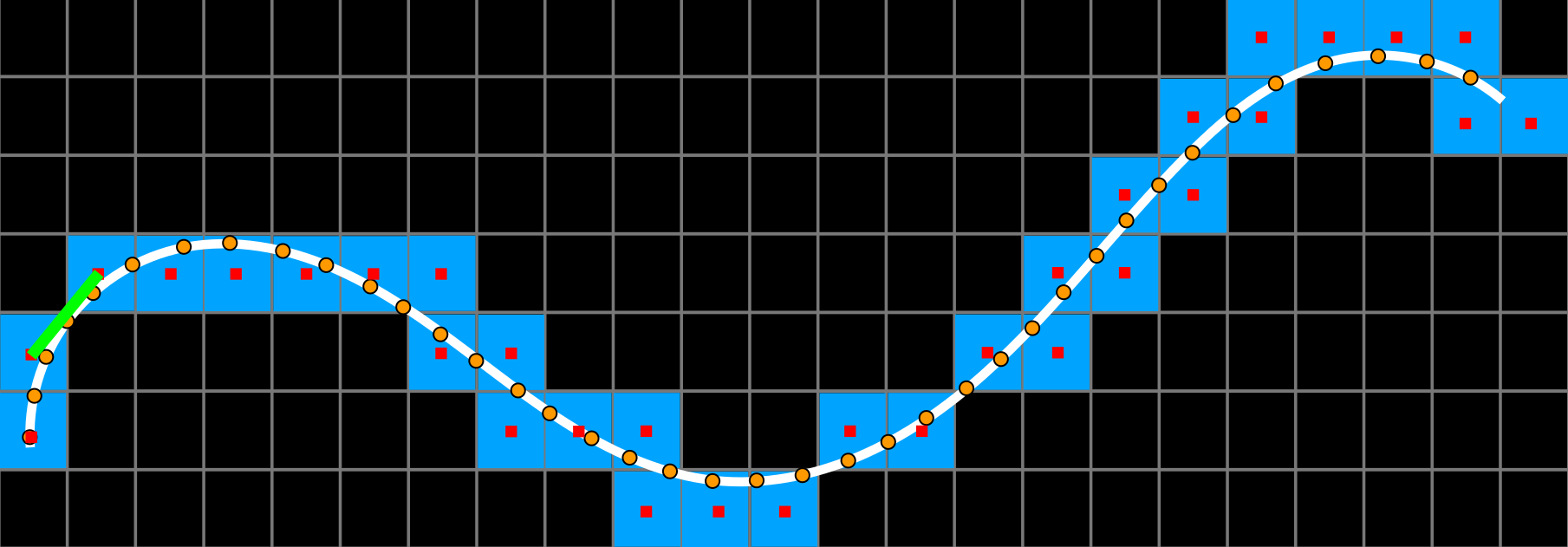
Curvature discretization
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
xi
x_i
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
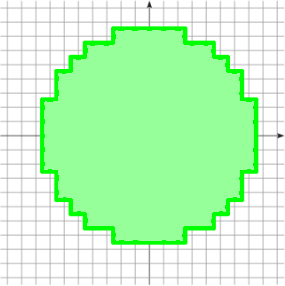
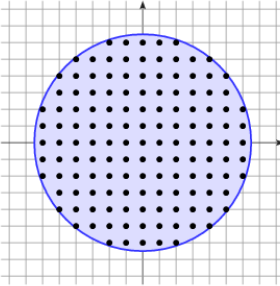
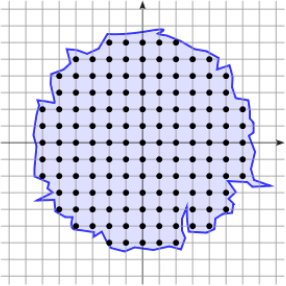
[Roussillon, 2011]
Digitization ambiguity
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Multigrid Convergence
∀x^∈∂hX with ∣∣x^−x∣∣∞≤h∣∣E^(Dh(X),x^,h)−E(X,x)∣∣≤τX(h)
\forall \hat{x} \in \partial_hX \text{ with } || \hat{x} - x ||_{\infty} \leq h\\
|| \hat{E}(D_h(X),\hat{x},h) - E(X,x)|| \leq \tau_{X}(h)
∃hX>0 such that, for any 0<h<hX and x∈∂X
\exists h_X > 0 \text{ such that, for any } 0 < h < h_X \text{ and } x \in \partial X
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
X
X
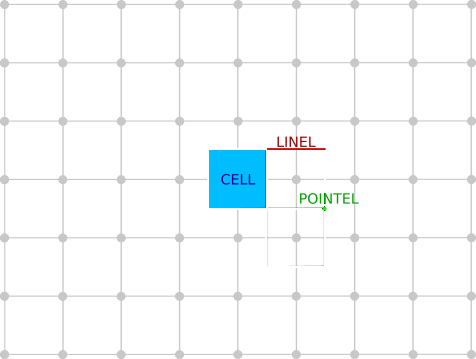
an euclidean shape
h-frontier of
grid step
digitization of X with grid step h
h
h
Dh(X)
D_h(X)
∂hX
\partial_h X
Dh(X)
D_h(X)
E(X,x)
E(X,x)
geometric quantity at point x of X
E^(D,x^,h)
\hat{E}(D,\hat{x},h)
estimated geometric quantity
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Integral based estimator for curvature
κ^R,h(xi)=R33(2πR2−Area(BR,h(xi)∩Dh))
\hat{\kappa}_{R,h}(x_i) = \frac{3}{R^3} \Big( \frac{\pi R^2}{2} - \widehat{Area} ( B_{R,h}(x_i) \cap D_h ) \Big)
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
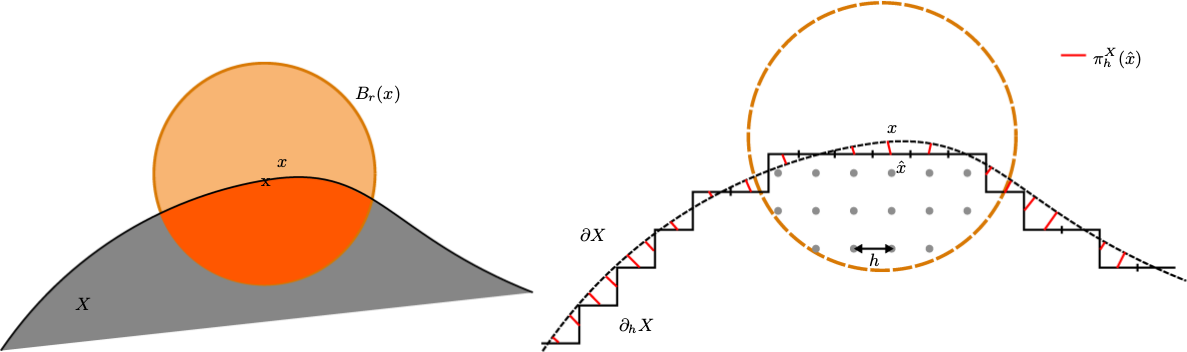
[Coeurjolly, 2013]
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Advantages of integral based estimator for curvature
Parameter free
Robustness to noise
Extendable to 3D
Simple formulation
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
To sum up
We want to use curvature as regularization term in models of image processing tasks
We believe that by using a multigrid convergent estimator, we can avoid some of the difficulties of adding curvature on the optimization process
1. Motivation problems
2. Regularization
3. Curvature regularization
4. Discretization and multigrid convergence
Introduction
Contribution
Conclusion
Digital Curvature Flow
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Model simplification
yminyj∈L∑k^R2(yj)⋅yj⋅s^(yj)
\displaystyle \min_{y} \sum_{y_j \in \mathcal{L}}{\hat{k}_R^2(y_j) \cdot y_j \cdot \hat{s}(y_j)}
subject to T,y∈{0,1}
\text{ subject to } T, y \in \{0,1\}
E(u)=∫Ω(u−g)2dx+∫∂uα+βκ2ds
\displaystyle E(u) = \int_{\Omega}{ ( u - g )^2 dx } + \int_{\partial u}{ \alpha + \beta \kappa^2 ds}
κ2ds
\displaystyle \kappa^2 ds
∫∂u
\displaystyle \int_{\partial u}
Consistency constraints
yminyi∈C∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}}{\hat{k}_R^2(y_i)}
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
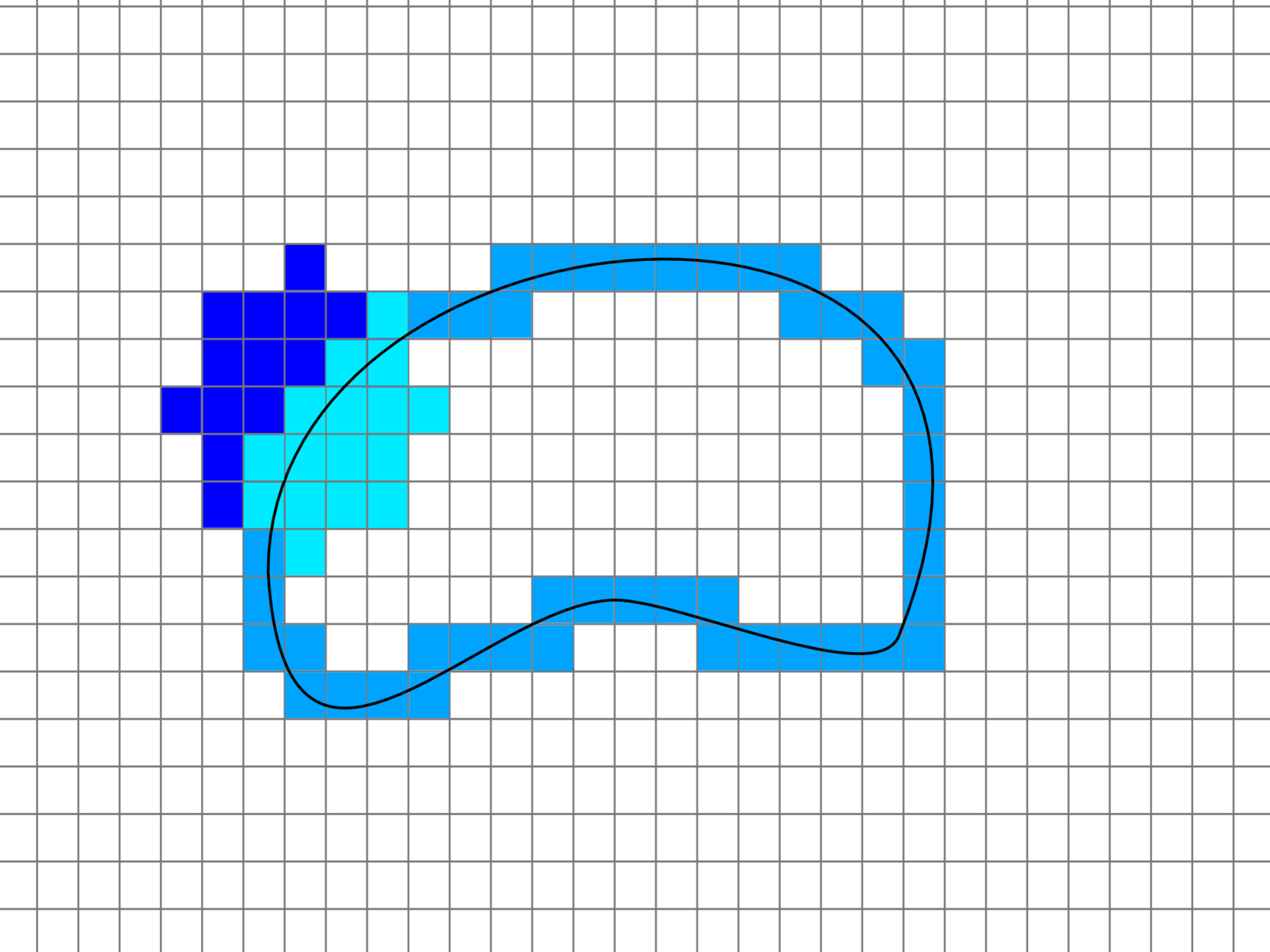
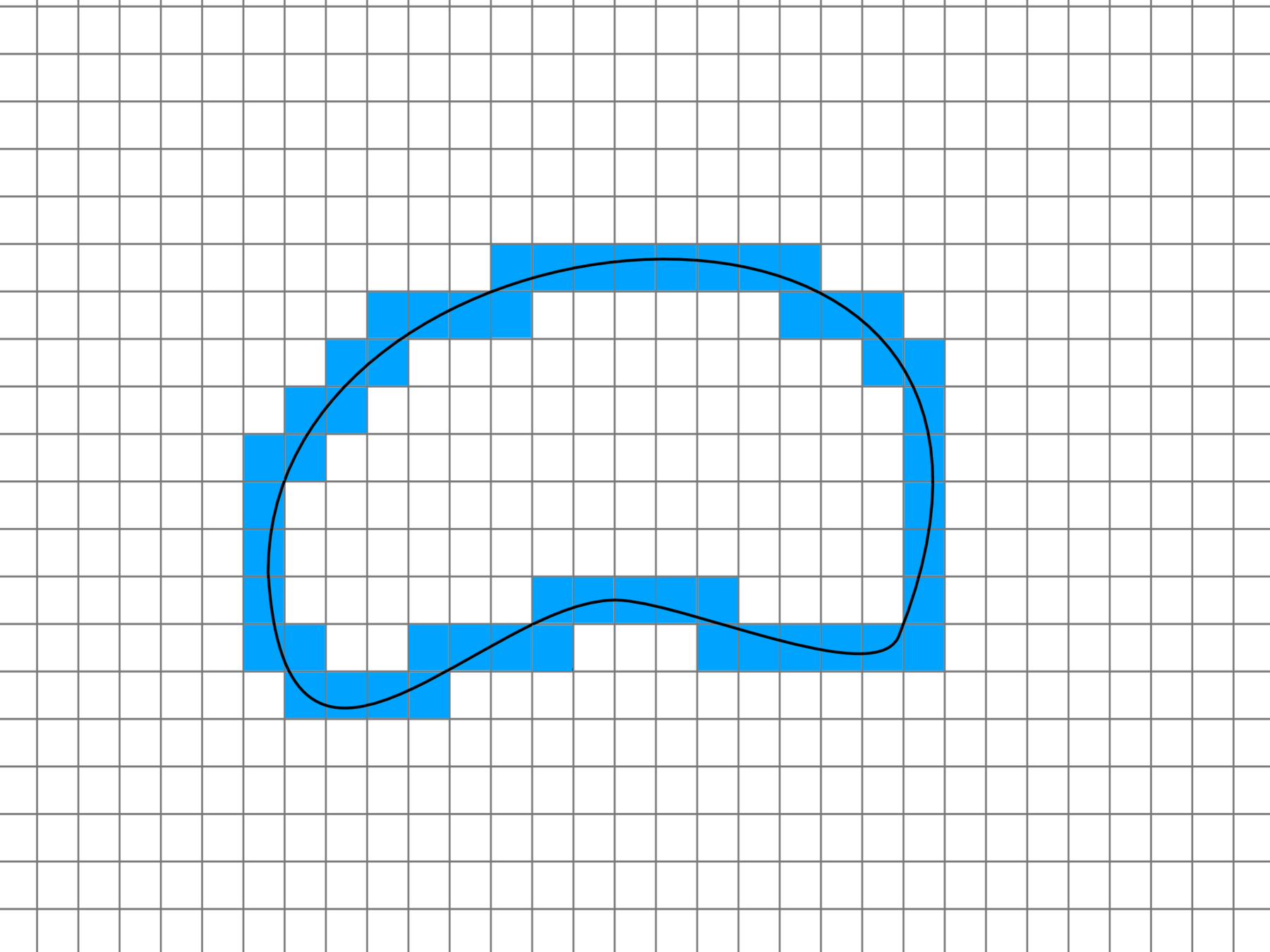
Curve evolution model
Given a connected digital shape , optimize its 4-connected pixel boundary accordingly with the energy
yminyi∈C(D)∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}
D
D
yminyi∈C(D)∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
yminp∈C(D)∑(1/2+∣Fr(p)∣−c2)⋅yi∈Yr(p)∑yi+yi,yj∈Yr(p);i<j∑yiyj
\displaystyle \min_{y} \sum_{p \in \mathcal{C}(D)}{ \left( (1/2+ |F_r(p)|-c_2) \cdot \sum_{y_i \in Y_r(p)}{y_i} + \sum_{ y_i,y_j \in Y_r(p); i < j }{y_iy_j} \right) }
yminyi∈C(D)∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{C}(D)}{\hat{k}_R^2(y_i)}
Non-submodular energy
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Curve evolution model
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
U
\displaystyle U
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Submodular set function
Let be a finite set and a set function. Function is submodular iff
f:2U→R
\displaystyle f:2^{U} \rightarrow \mathbb{R}
f(A∪{b})−f(A)≥f(A∪{b,c})−f(A∪{c})
\displaystyle f(A \cup \{b\}) - f(A) \geq f(A \cup \{b,c\} ) - f(A \cup \{c\})
for all A⊂Ω,b=c∈Ω∖A
\displaystyle \text{for all } A \subset \Omega, b \neq c \in \Omega \setminus A
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Quadratic pseudo-boolean function
∀i,jEi,j(0,1)−Ei,j(0,0)≥Ei,j(1,1)−Ei,j(1,0)
\displaystyle \forall i,j \quad E_{i,j}(0,1) - E_{i,j}(0,0) \geq E_{i,j}(1,1) - E_{i,j}(1,0)
E:{0,1}n→R,yi∈Y∑Ei(yi)+yi,yj∈Y;i<j∑Ei,j(yi,yj)
\displaystyle E:\{0,1\}^n \rightarrow \mathbb{R}, \quad \sum_{y_i \in Y}{ E_i(y_i) } + \sum_{ y_i,y_j \in Y; i < j }{E_{i,j}(y_i,y_j)}
Definition: Function E is regular if
Submodular set functions is a subclass of QPSB functions, namely those that are regular.
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Quadratic pseudo-boolean function
Submodular (regular) functions can be optimized in polynomial time
The optimization of a general non-submodular function is NP-Hard
A technique called Roof Duality may find a partial solution. Such solution is guaranteed to be a subset of some optimal solution
p∈O∑(1/2+∣Fr(p)∣−c2)⋅yi∈Yr(p)∑yi+yi,yj∈Yr(p);i<j∑yiyj is non-submodular Ei,j(0,1)−Ei,j(0,0)≥Ei,j(1,1)−Ei,j(1,0)for some i,j0−0≥1−0
\displaystyle \sum_{p \in \mathcal{O}}{ \left( (1/2+ |F_r(p)|-c_2) \cdot \sum_{y_i \in Y_r(p)}{y_i} + \sum_{ y_i,y_j \in Y_r(p); i < j }{y_iy_j} \right) } \\
\text{ is non-submodular }\\
\\
E_{i,j}(0,1) - E_{i,j}(0,0) \geq E_{i,j}(1,1) - E_{i,j}(1,0)\\
\text{for some } i,j \quad 0 - 0 \not\geq 1 - 0
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Quadratic pseudo-boolean function
QPBOP: Returns partial solution. Some pixels are not labeled.
QPBOI: Improves a partial solution value and returns a full labeling. Partial optimality property is loss.
If energy is submodular, QPBOP labels all variables.
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Optimization region
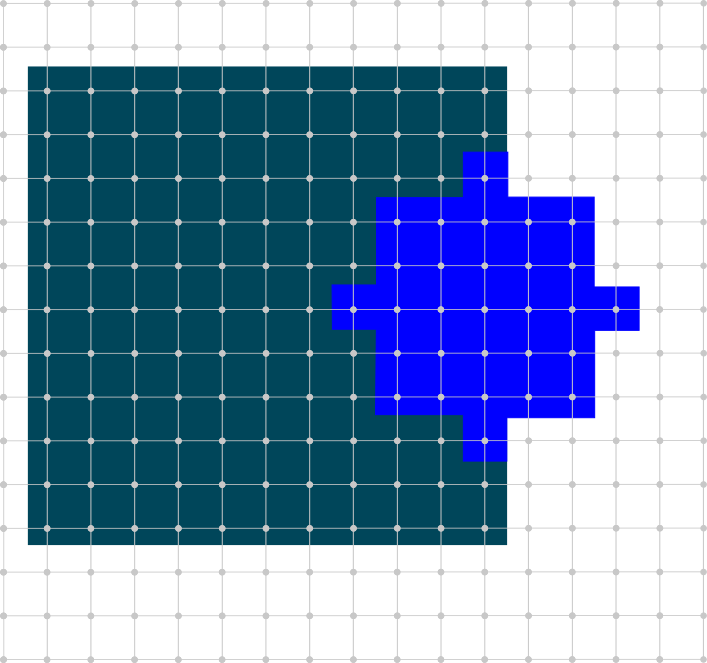
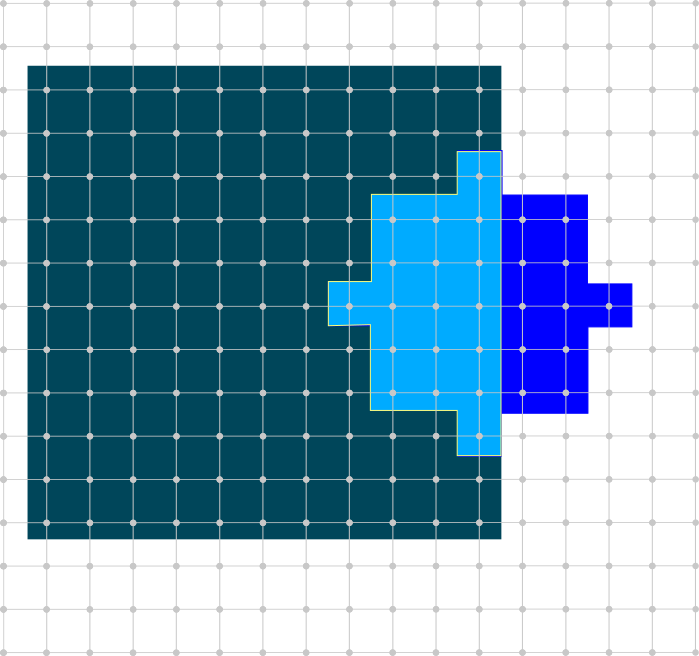
It is not symmetric
O
\mathcal{O}
κ^R,h(xi)=R33(2πR2−Area(BR,h(xi)∩Dh))
\hat{\kappa}_{R,h}(x_i) = \frac{3}{R^3} \Big( \frac{\pi R^2}{2} - \widehat{Area} ( B_{R,h}(x_i) \cap D_h ) \Big)
Trusty foreground
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Curve evolution model
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Curve evolution model
Convex regions are removed. Flat and concave regions stays the same
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Sensible regions indication
yminyi∈O∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{O}}{\hat{k}_R^2(y_i)}
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
yminαyi∈O∑k^R2(yi)+βyi∈O∑yj∈N4(yi)∑(yi−yj)2
\displaystyle \min_{y} \alpha \sum_{y_i \in \mathcal{O}}{\hat{k}_R^2(y_i)} + \beta \sum_{y_i \in \mathcal{O}}\sum_{y_j \in \mathcal{N}_4(y_i)}{ (y_i-y_j)^2}
yminyi∈O∑k^R2(yi)
\displaystyle \min_{y} \sum_{y_i \in \mathcal{O}}{\hat{k}_R^2(y_i)}
α=1β=0.5
\alpha=1\\
\beta=0.5
α=1β=1.0
\alpha=1\\
\beta=1.0
α=1β=2.0
\alpha=1\\
\beta=2.0
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Perimeter regularization
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Optimization region
O
\mathcal{O}
Trusty foreground
Computation Region
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Filtering artifacts
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Level expand-correct evolution
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Level expand-correct evolution
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Unlabeled pixels
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Segmentation post-processing
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Segmentation post-processing
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Model summary
Curvature regularization using multigrid convergent
estimator
Post-processing step in image segmentation
Works well with extra terms ( data fidelity, perimeter )
Too local. Completion property is not recovered
Digital Curvature Flow
Introduction
Contribution
Conclusion
1. Model
2. Non-submodular functions
3. Interpretation
4. Applications and discussion
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
Take-home message
Regularization is a classical approach to solve inverse problems, including those of image processing;
Non-convex terms can be useful, but optimization is non trivial;
Completion property of curvature is achieved in a global optimization framework.
Multigrid convergent estimators should be preferred when working with digital data;
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Thank you for your attention!
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
What to do next
Global optimization model
subject to T,x∈{0,1}
\text{ subject to } T, x \in \{0,1\}
Linearization + Relaxation + LP solver
Partial linearization + Relaxation + Penalization + QSolver
Linearization + Partial Relaxation + Branch and Bound
yminyi∈L∑yi⋅C1+C2⋅yj∈C∑yj+yj,yk∈C∑yjyk
\displaystyle \min_{y} { \sum_{y_i \in \mathcal{L} } y_i \cdot \left( C_1 + C_2 \cdot \sum_{y_j \in \mathcal{C} }{y_j} + \sum_{y_j,y_k \in \mathcal{C} }{y_jy_k} \right) }
yminαyi∈C∑D(yi)+βyj∈L∑k^R2(yj)⋅yj⋅s^(yj)
\displaystyle \min_{y} \alpha\sum_{y_i \in \mathcal{C} }{ D(y_i) } + \beta\sum_{y_j \in \mathcal{L}}{\hat{k}_R^2(y_j) \cdot y_j \cdot \hat{s}(y_j)}
Optimize submodular approximation of the energy
?
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
What to do next
Relation with Thresholding Dynamics
Daniel Martins Antunes
Seminar LIMD, March 21, 2019
Digital Curvature Flow
Introduction
Contribution
Conclusion
What to do next
Discrete calculus formulation
Digital Curvature Flow Daniel Martins Antunes Université Savoie Mont Blanc, LAMA Seminar LIMD March 21, 2019
Digital Curvature Flow
By Daniel Martins Antunes
Digital Curvature Flow
A preliminary version of the slides of DGCI. It was presented at LAMA during the seminar of the LIMD research group.
- 219
