A Kinetic Neural Network Approach for Absolute Quantification and Change Detection in Positron Emission Tomography

D. Poggiali, postDoc

Roma, MASCOT18

Davide Poggiali, Diego Cecchin and Stefano De Marchi

Summary:

Introduction
Kinetics of the tracer in PET/MRI
A new approach to kinetical modelling
Results
Conclusions & future works

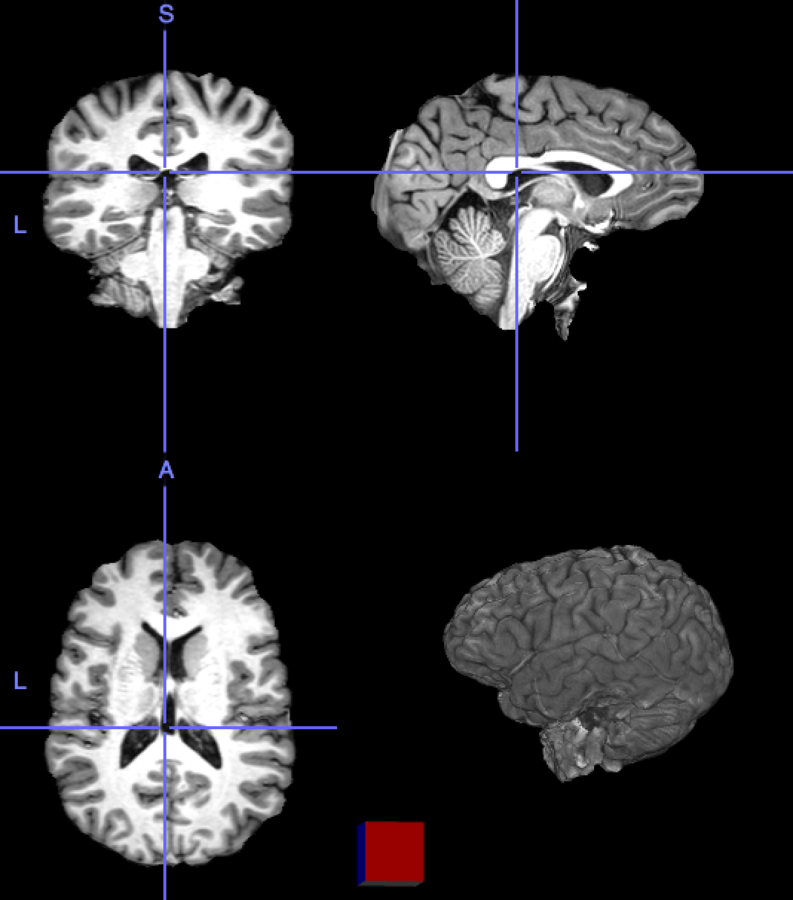
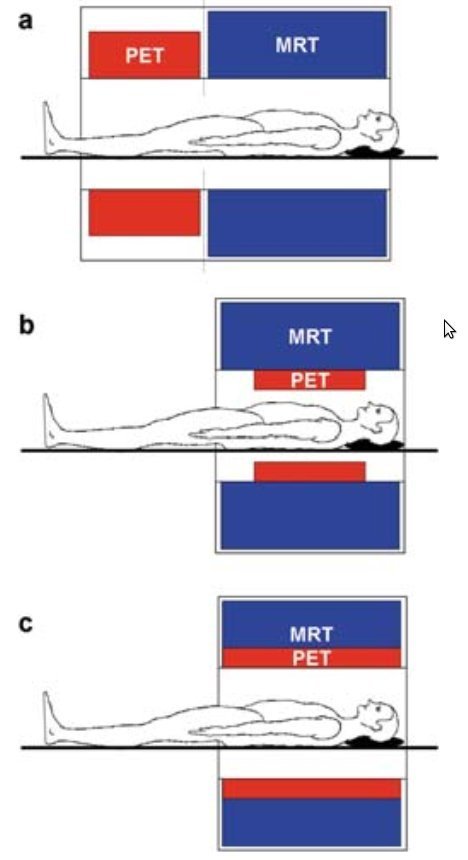
What is PET/MRI?

1. Introduction

Motivation: The PET Grand Challenge 2018

Dataset:

5 simulated PET/MRIs
dynamic PET images
pre and post intervention
unknown tracer

Aim:

"to identify areas and magnitude of receptor binding changes in a PET radioligand neurotransmission study"

2. Kinetics of the tracer in PET/MRI

Tracer kinetics is studied with ODE compartment model

A compartment is a set of tissues that exchanges energy/material to another set of tissues at the same rate

K=\frac{k_1k_3}{k_1+k_2}

A classical example: Sokoloff model (1970s)

\left\lbrace {\begin{array}{ccccc} \dot{C_p} = & u(t) & -k_1 C_p &+ k_2 C_f & \\ \dot{C_f} = & & k_1 C_p &- k_2 C_f & - k_3 C_f\\ \dot{C_b} = & & & &k_3 C_f\\ \end{array} } \right.

Absolute Metabolic rate:

A= \left[ {\begin{array}{cc} -k_1 & k_2 & 0\\ k_1 & -(k_2+k_3) & 0\\ 0 & k_3&0 \end{array} } \right]

B= \left[ {\begin{array}{cc} 1 & 0 & 0 \end{array} } \right]'

C= \left[ {\begin{array}{cc} V_b & 1-V_b & 1-V_b \end{array} } \right]

\left\lbrace {\begin{array}{cc} \dot{x} = &Ax + B u\\ y = &Cx \end{array} } \right.

General compartmental model formulation

Solution of the general model

u\equiv 0

in case

\dot{x}= Ax \;\;\longrightarrow \;\; x(t) = \exp(At)

else

\dot{x}= Ax +Bu \;\longrightarrow \; x(t) = \exp(At) \int_0^t \exp(-A\tau)Bu(\tau)d\tau

y(t) = C\int_0^t \exp(A(t-\tau))Bu(\tau)\;d\tau =

= \left( C \exp(At) B \right) \ast u(t) = \phi(t) \ast u(t)

3. A new approach to kinetical modelling

What do you see?

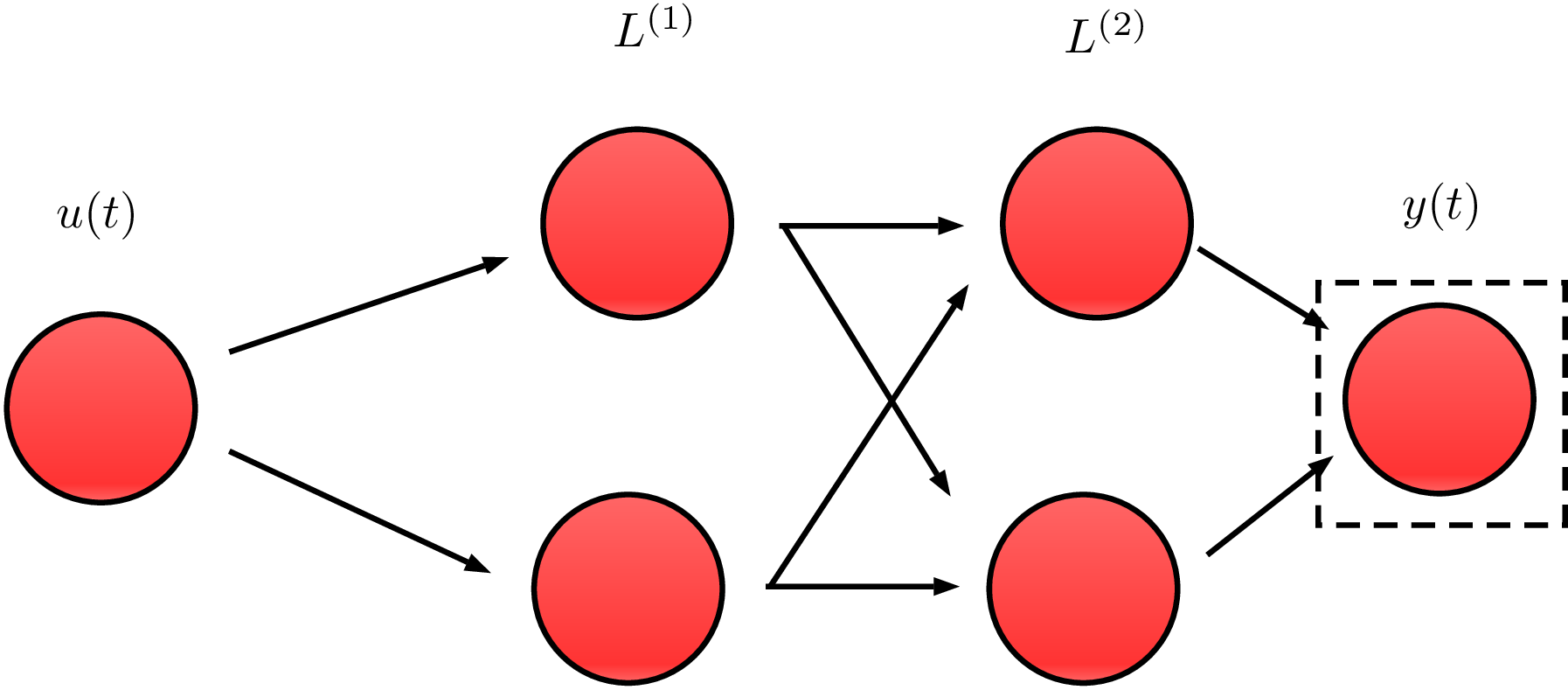
(Almost) any graph-based model is applicable

In this work we propose neural networks graphs.

Simplest example: this 2x2 network.

Issue #1: the exponential matrix is heavier to compute as the size of the network grows.

Hence we use the Padé approximation

\displaystyle N_{p,q}(A) = \sum_{j=0}^p \frac{(p+q-j)!\;p!}{(p+q)!\;j!\;(p-j)!} A^j

\displaystyle D_{p,q}(A) = \sum_{j=0}^q \frac{(p+q-j)!\;q!}{(p+q)!\;j!\;(q-j)!} (-A)^j

\exp(A) \approx F_{p,q}(A) = N_{p,q}(A)^{-1} D_{p,q}(A)

||A|| < 5.4 \;\;\longrightarrow || \exp(A) - F_{13,13}(A)|| < 10^{-16}

Theorem:

This condition is true in 2x2 case as

||At||_\infty \leq 4.5 \;\; \forall t \leq 1.5

import sympy as s
k11,k12,k21,k22 = s.symbols('k11,k12,k21,k22')
k1,k2,t = s.symbols('k1,k2,t')

A = s.SparseMatrix([[-(k11+k12),0, 0,0],
                    [0,-(k21+k22), 0,0],
                    [k11,k12,      0,0],
                    [k21,k22,      0,0]])

B = s.Matrix([1/3,2/3,0,0])
C = s.Matrix([0,0,k1,k2]).T

Issue #2: A general framework for parameter estimation is needed.

Gradient descent algorithm:

y_\theta = \phi_\theta \ast u

Cost function:

\displaystyle J(\theta) = \frac{1}{2n_t} \sum_{i=1}^{n_t} \left(y_{\theta,i} -y_i\right)^2

\displaystyle \theta \leftarrow \theta - \alpha \;\nabla_\theta J

\displaystyle \frac{\partial J}{\partial\theta_j} = \frac{1}{n_t} \sum_{i=1}^{n_t} \left(y_{\theta,i} -y_i\right) \frac{\partial y_{\theta,i}}{\partial \theta_j} = \frac{1}{n_t} \sum_{i=1}^{n_t} \left(y_{\theta,i} -y_i\right) \frac{\partial \phi_{\theta,i}}{\partial \theta_j} \ast u(t)

import numpy as np
from scipy impoer convolve1d

def grad_obj(x):
    Ph=[]; Gr=[]
    for i in range(len(x)):
        Ph+=[Phi(x[i])]
        Gr+=[Part(x[i])]
 
    Gr_est=convolve1d(Gr,u,axis=1).T
    y_est=convolve1d(Ph,u,axis=1).T
 
    err=y_est-y
    grad_ob=(np.sum(err*Gr,axis=1).T)/err.shape[1]
    return grad_ob

Issue #3: The image size is (182, 218, 182, 23)...

about 7 million voxels per timepoint!

An iterative refinement strategy has been adopted.

Level = 8

Level = 4

Level = 2

Level = 1

4. Results

Hotelling p-value has been calculated for all image pairs in a voxel-wise manner.

A confidence level of 0.05 has been used.

\displaystyle \Sigma = \frac{(n_x -1) \Sigma_x + (n_y -1) \Sigma_y}{n_x+n_y-2}

\displaystyle T^2 = \frac{n_x n_y}{n_x +n_y} (\bar{x}-\bar{y})\Sigma^{-1}(\bar{x}-\bar{y})

5. Conclusions &

future works

Conclusions:

A general graph-based framework for PET parameter estimation has been written in Python.
Voxel-level parameters has showed interesting results in change-detection problem, regardless of the tracer.

Future work:

Compare the framework's result with commonly-used methods
Use the framework in other context (e.g. brain tumors)
Re-write in dask the framework for scalability (parallel/cluster/GPU computing) and computation time reduction
Test bigger networks

Thank you!

I want to thank for their support:

E. Arbitrio, S. Basso, P. Gallo, E. Perracchione, F. Rinaldi.

References

[1] M. Arioli, B. Codenotti, and C. Fassino, The Padé method for computing the matrix exponential, Linear Algebra and its Applications, 240 (1996), pp. 111–130.

[2] A. Meurer, C. P. Smith, M. Paprocki, et al., SymPy: symbolic computing in Python, PeerJ Computer Science,3 (2017), p. e103.

[3] C. S. Patlak, R. G. Blasberg, and J. D. Fenstermacher, Graphical Evaluation of Blood-to-Brain Transfer Constants from Multiple-Time Uptake Data, Journal of Cerebral Blood Flow & Metabolism, 3 (1983), pp. 1–7.

[4] G. L. Zeng, A. Hernandez, D. J. Kadrmas, and G. T. Gullberg,

Kinetic parameter estimation using a closed-form expression via integration by parts, Physics in medicine and biology, 57 (2012), pp. 5809–21