Fake Nodes approximation for Magnetic Particle Imaging

Stefano De Marchi, Wolfgang Erb, Francesco Marchetti,

Elisa Francomano, Emma  Perracchione, Davide Poggiali

D. Poggiali, postDoc

MELECON 2020

Summary:

  1. Reconstruction in MPI
  2. Fake Nodes interpolation
  3. Numerical experiments
  4. Results and future works

Slides are available online

https://slides.com/davidepoggiali/melecon2020

http://dpoggiali.altervista.org

to check out other work of mine.

1. Reconstruction in MPI

Magnetic Particle Imaging (MPI) is a tracer-based tomographic technique of recent development. MPI systems detect the spatial distribution of superparamagnetic nanoparticle tracers injected in the body.


Image acquisition in MPI is performed by generating a magnetic Field Free Point (FFP), moving along a chosen curve \(\gamma(t)\) and inducing a measurable voltage signal in a receive coil.

 

The scattered data obtained from this signal acquisition process can then be interpolated and evaluated over a regular grid to get a human-readable image; we will refer to this interpolation process as reconstruction.

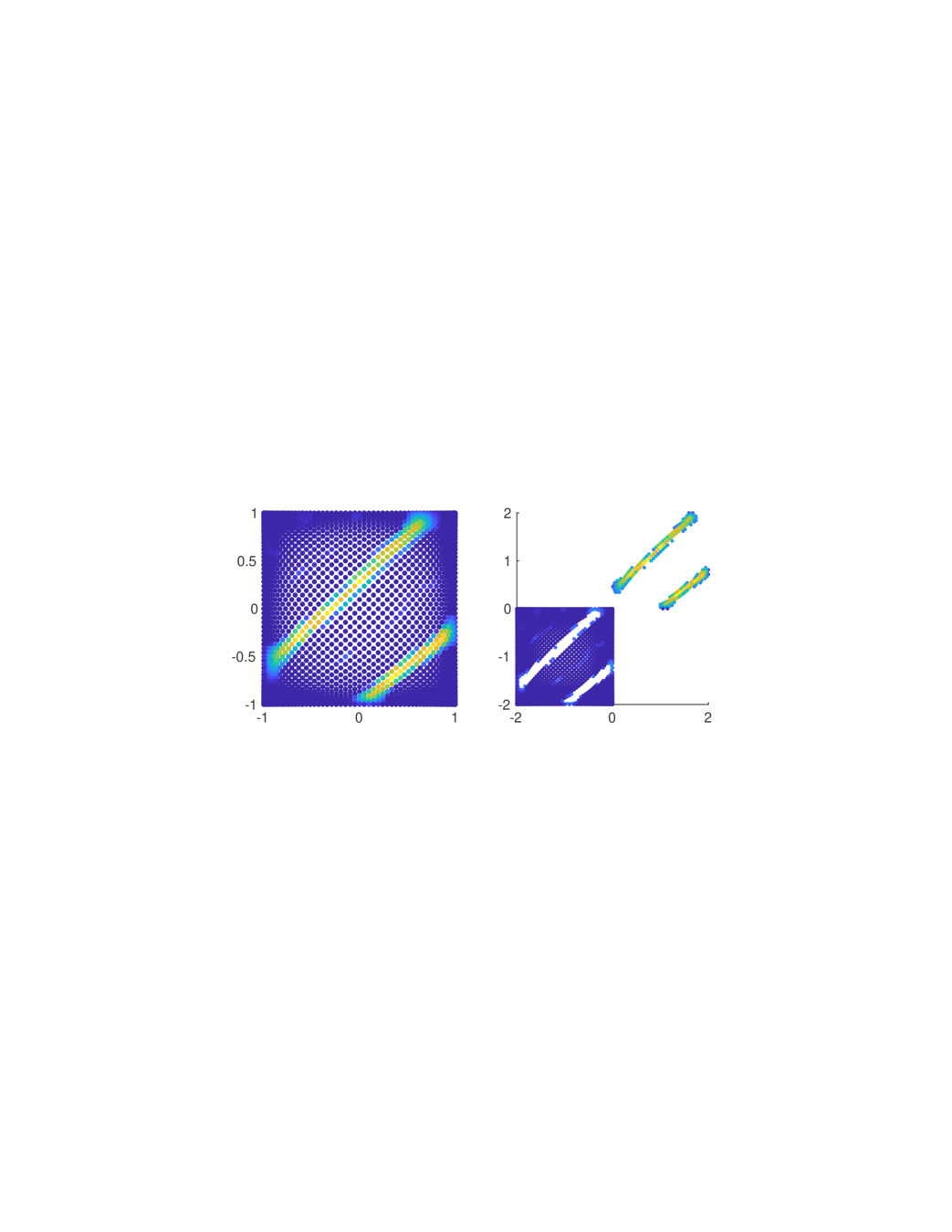
Commonly-used trajectories in MPI are Lissajous curves

\gamma(t)= \left( \cos (n_2t ), \, \cos \left( n_1 t - \frac{\epsilon-1}{2n_2}\pi \right) \right) \\ t \in [0, 2\pi], \; \epsilon \in \{ 1,2 \}, \; n_1, n_2 \in \mathbb{N}
\mathrm{LS} = \left\{\gamma\left(\frac{\pi k}{\epsilon n_1n_2}\right), \quad k=0,\ldots,2\epsilon n_1n_2-1 \right\}.

The sampling points are the so-called Lissajous nodes

2. Fake Nodes interpolation

Interpolation on Fake Nodes, or interpolation via Mapped Bases is a technique that applies to any interpolation method. It has shown in many cases the ability of obtaining a better interpolation without getting new samples.

 

 This means that, provided that the original nodes are a sufficient sample of the given signal, it can be possible in principle to provide a more stable or accurate interpolation.

Fake Nodes interpolation

In terms of code: suppose that you have a generic interpolation function ...

def my_fancy_interpolator(x,y,xx):
  .......
  .......
  return yy

def my_fancy_interpolator(x,y,xx):
  p = np.polyfit(x,y)
  yy = np.polyval(p,xx)
  return yy

instead of calling the function directly you define a mapping function S and interpolate over the fake nodes S(x)
 

f = lambda x: np.log(x**2+1)
x = np.linspace(-1,1,10)
y = f(x)
xx = np.linspace(-1,1,100)



yy = my_fancy_interpolator(x,y,xx)
f = lambda x: np.log(x**2+1)
x = np.linspace(-1,1,10)
y = f(x)
xx = np.linspace(-1,1,100)

S = lambda x: -np.cos(np.pi * .5 * (x+1))

yy = my_fancy_interpolator(S(x),y,S(xx))

In other words, given a function

f: \Omega \subseteq \mathbb{R}^d \longrightarrow \mathbb{R}\;\;\;\;\; {d \in \mathbb{N}},

a set of distinct nodes

X = \{ x_0, \dots, x_N\} \subset \Omega,

and a set of basis functions

\mathcal{B} = \{ b_i: \Omega \longrightarrow \mathbb{R} \}_{i = 0, \ldots, N}

The interpolant is given by a function

\displaystyle \mathcal{P}(\bm{x}) = \sum_{i=0}^{N} c_i b_i(\bm{x})

s.t.

\mathcal{P}(\bm{x}_i)=y_i:=f(\bm{x}_i) \;\;\forall i
\mathcal{B} = \{ b_i \circ S: \Omega \longrightarrow \mathbb{R}^d \}_{i = 0, \ldots, N}
\displaystyle \mathcal{R}^s(\bm{x}) = \sum_{i=0}^{N} c_i b_i(S(\bm{x}))
\mathcal{R}^s(\bm{x}_i)=y_i:=f(\bm{x}_i) \;\;\forall i

This process can be seen equivalently as:

1. Interpolation over the mapped basis

\[\mathcal{B}^s = \{b_i \circ S \}_{i=0, \dots, N}.\]

2. Interpolation over the original basis \(\mathcal{B}\) of a function \(g: S(\Omega) \longrightarrow\mathbb{R}\)

at the fake nodes 

\[S(X) = \{S(x_i) \}_{i=0, \dots, N}.\]

 \(g\in C^s\) must satisfy \(g(S(x_i)) = f(x_i)\;\;\forall i\).

If \(\mathcal{P} \approx g \) on \(S(X)\) with the original basis,

then \(\mathcal{R}^s = \mathcal{P} \circ S \approx f \)  on \(X\)

3. Numerical experiments

A set of simulated MPI data whose ground truth is known has been generated, with parameters \(n_1 = 33, n_2 = 32, \epsilon=2\). Reconstruction has been performed on a 201x201 equispaced grid with different interpolation methods. Results have been compared to the ground truth.

Bivariate polynomial interpolation:

\(\mathcal{B} = \left \lbrace x_1^i x_2^j  \right|\left. i,j = 0,\dots,K\text{  s.t.  } i+j\leq K \right\rbrace\)

we used least-squares approximation with \(K=21\).

RBF interpolation:

\(\mathcal{B} = \left \lbrace K(\cdot, \bm{x}_i) \right\rbrace_{i = 0,\dots,N}.\)

being \(K(\cdot, \bm{x}_i) = \varphi(\|\cdot - \bm{x}_i\|_2)\) a kernel function.

 

we choose the Matérn functions of different regularities:

  • \(\varphi_0(r)=\exp(-r) \in C^0\)
  •  \( \varphi_2(r)=\exp(-r)(1+r) \in C^2\)
  •  \(\varphi_4(r)=\exp(-r)(3 + 3r + r^2 ) \in C^4\)
  •  \(\varphi_6(r)=\exp(-r)(15 + 15r + 6r^2) \in C^6\)
\displaystyle S(x) = x + \sum_{k=1}^m \alpha_k \chi_{\Gamma_k}(x)
\alpha_k \coloneqq k (a,a)\;\;\; a>diam(\Omega)

Since our signal is discontinuous, its reconstruction will be affected by Gibbs phenomenon. To prevent this effect we used Fake Nodes interpolation with mapping \(S\) chosen as

being \(\Gamma_k\) the non-overlapping sets given by the segmentation of the image.

Symmetrized Kullbak-Leibner Divergence has been used for performance comparison.

where the Kullbak-Leibner Divergence is defined as

SKL(A,I) = KL(A,I) + KL(I,A)
KL(v,w) = \displaystyle\frac{\displaystyle\sum_{i=1}^{K} w_i \log\left(\frac{v_i}{w_i}\right)}{K}

4. Results and future works:

Polynomial approximation (left) and polynomial+Fake Nodes (right)

RBF \(C^0\) interpolation (left) and Fake-RBF \(C^0\) (right)

Method SKL (smaller is better)
 Polynomial 1.3581
 Fake-Polynomial 0.6424
RBF C⁰ 0.7369
Fake-RBF C⁰ 0.6833
RBF C² 0.7947
Fake-RBF C² 0.8117
RBF C⁴ 0.8050
Fake-RBF C⁴ 0.9137
RBF C⁶ 1.0779
Fake-RBF C⁶ 1.0154

 Future works:

 

Fake Nodes interpolation can be further investigated.

MPI reconstruction:

  • Other RBF with different shape parameters,
  • kernel Moving Least Squares.

Other bio-medical applications:

  • image denoising,
  • resolution approximation of an imaging system,
  • MEG/EEG reconstruction.

 

References

[1] J P. Berrut, S. De Marchi, G. Elefante, F. Marchetti, Treating the Gibbs phenomenon in barycentric rational interpolation and approximation via the S-Gibbs algorithm. Applied Math. Letters, 2020.

[2] W. Erb, Bivariate Lagrange interpolation at the node points of Lissajous curves - the degenerate case, Appl. Math. Comput. 2016

[3] S. De Marchi, W. Erb, F. Marchetti, Lissajous sampling and spectral filtering in MPI applications: the reconstruction algorithm for reducing the Gibbs phenomenon, 2017 International Conference on Sampling Theory and Applications (SampTA), Tallin (2017).

[4] S. De Marchi, F. Marchetti, E. Perracchione, D. Poggiali, Polynomial interpolation via mapped bases without resampling, JCAM 2020.

[5] S. De Marchi, W. Erb, F. Marchetti, E. Perracchione, M. Rossini, Shape-Driven Interpolation with Discontinuous Kernels: Error Analysis, Edge Extraction and Applications in MPI, SIAM Sci. Comput. 2020

Thank you for your attention!

MELECON2020

By davide poggiali

Made with Slides.com

MELECON2020

Money and fear? Never had either

  • 625

More from davide poggiali