Toward a Theory of Causation for Interpreting Neural Code Models
Journal-First
April 30, 2025
David N. Palacio
Alejandro Velasco
Nathan Cooper
\Phi
Alvaro Rodriguez
Kevin Moran
Denys Poshyvanyk
Causal Interpretability
To what extent is the current prevalence of code generation driven by Hype?
Explaining why a Neural Code Model makes the predictions it does has emerged as one of the most challenging questions in DL4SE
(Palacio. et al., 2023) (Lipton,2017) (Pearl,2016)
Motivating Example:
Buggy Code → Code Prediction
def countChars(string, character):
count = 0
for letter in string:
if letter = character:
count = count + 1
return count
feasible correct snippet
codegen-mono-2b
def countChars(string, character):
count = 0
for letter in string:
if letter = character:
count = count - 1
return count
feasible buggy snippet (line 5)
=
count
+
-
0.4
0.6
0.01
0.01
0.5
0.4
0.01
0.01
0.05
0.04
0.01
0.8
0.05
0.04
0.01
0.8
p(w_{t+1}|w_{< t-2})
p(w_{t+2}|w_{< t-3})
p(w_{t+3}|w_{< t-4})
correct snippet
buggy snippet
count
=
+
-
=
+
-
T_1
T_0
context
def
...
[case A]: To what extent does a buggy sequence impact error learning or code prediction?
T
Treatment:
Bugs in Code
Y = p(w_{t}|w_{< t})
Potential Outcome:
Code Prediction
?
\tau_{i} = Y_{i}^{Fixed} - Y_{i}^{Buggy}
"T causes Y if Y listens to T":
If we change T, we also have to observe a change in Y (Pearl, 2019)
average causal effect ?
The Causal Effect is a measure of the influence of a variable T on another variable Y .
We propose using scientific explanations based on causality to reduce the conceptual interpretability gap
\Phi
Factors or Treatments
Outcomes
Causal Effect or Explanation
Type of Prompts, Hyperparameters,
or SE Interventions
Correlations,
ATEs,
or Counterfactual Pr.
Accuracy,
Logits,
or Predictions
Interpretability is understanding how and why models make predictions so that decision-makers (e.g., programmers, doctors, judges) can assess the extent to which they can trust models' output
(Doshi-Velez & Kim, 2017) (Weller,2019) (Lipton,2017) (Pearl,2019)
How do we interpret Neural Code Models with Scientific Explanations?
Pearl's Ladder of Causation
Rung/Level 1
Rung/Level 2
Rung/Level 3
Associational
Interpretability
Interventional
Interpretability
Counterfactual
Interpretability
Q_1 = P(Y|T)
Q_2 = P(Y|do\{T\})
Q_3 = P(y_t|t',y')
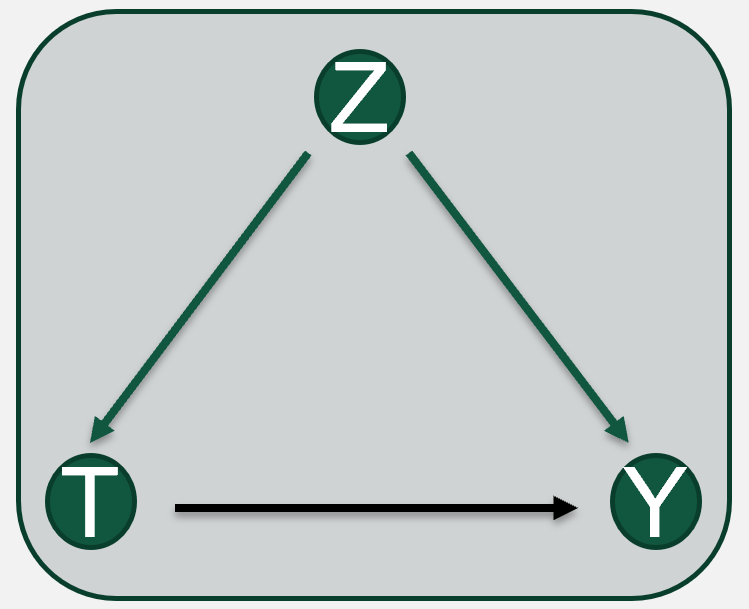
How is the code prediction Y related to (testing) code data with bugs T ?
To what extent does a (test) buggy sequence impact error learning or code prediction?
Would the model generate accurate code predictions if bugs had been removed from training code data?
Causal Interpretability occurs at different levels
Causal Inference helps us to control for confounding bias using graphical methods
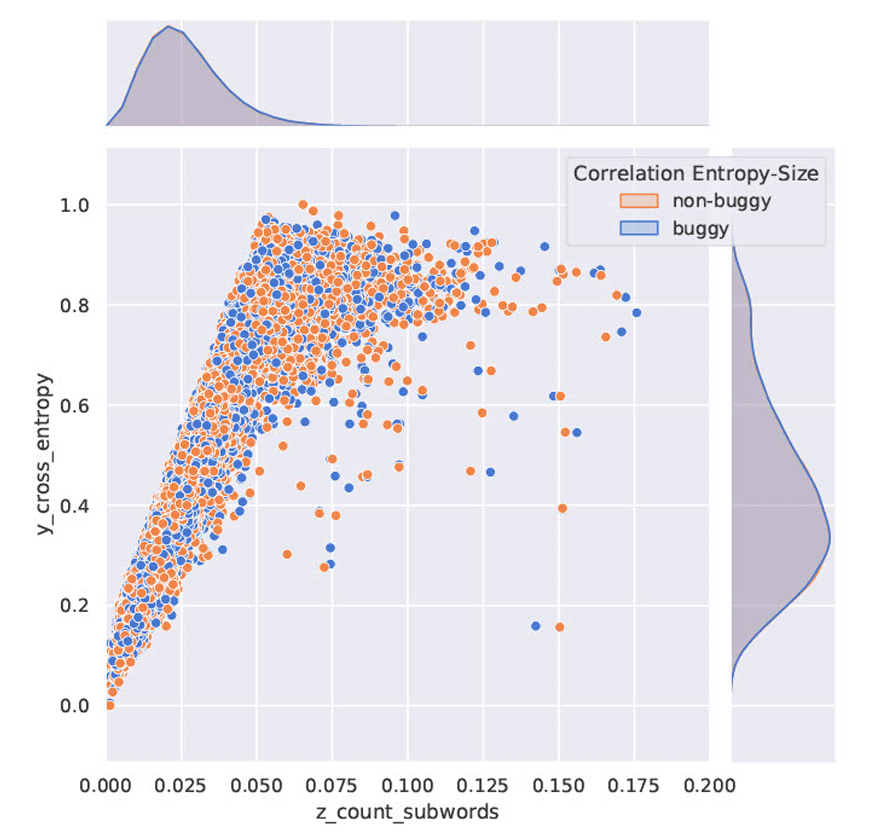
After sequence size control, test data with buggy code is negatively affecting code predictions of syntax operators {'+','-'} by 40%
Causal Explanation for the generated code:
T
Treatment:
Bugs in Code
Y = p(w_{t}|w_{< t})
Potential Outcome:
Code Prediction
Z
Confounder:
Sequence Size
causal effect = -0.4
The Causal Interpretability Hypothesis
doCode is a causal interpretability method/methodology that aims to make Deep Learning for Software Engineering (DL4SE) systems (e.g., pretrained or LLMs) and their decision-making process understandable for researchers and practitioners
Approach
The math of doCode
Step 1: Modeling Causal Problem
Endogenous nodes can be employed to model relationships among interpretability variables
Structural Causal Model for Interpretability (SCMi)
T
Y
Z
treatments
potential outcomes
confounders
Graph Criteria
SE-based (interpretability) interventions
Representation of code predictions
Variables that affects both proposed SE-based interventions and code predictions
BuggyCode
Cross-Entropy Loss
Sequence Size
causal effect
Step 2: Identifying Causal Estimand
Level 1: Association
Conditional Probability
causal effect
\tau = p(Y|do\{T\})
FixedCode
treatments
potential outcomes
confounders
causal effect
\tau = p(Y|T)
Variable Z is controled
graph surgery/mutilation
Level 2: Intervention
Interventional Probability
Adjustment Formula or Estimand
p(Y|do\{T\}) = \sum_zp(Y|t,z)p(z)
Interventional Distribution (Level 2)
p(Y|T) = \sum_zp(Y|t,z)p(z|t)
Observational Distribution (Level 1)
back-door criterion
(algebraic + statistical properties)
Step 3: Estimating Causal Effects
p(y|do\{t\})
Interventional Distribution for one data sample
We can use the adjustment formula to compute or estimate causal effects from observational data (Pearl, et al., 2016)
p(y|do\{t\})
Interventional Distribution for one data sample
E_{i\sim p(i)}[Y=y|i,do\{T=t\}]
We can compute for a set of samples (i.e., code snippets) obtaining an ATE (average treatment effect)
We can use the adjustment formula to compute or estimate causal effects from observational data (Pearl, et al., 2016)
p(y|do\{t\})
Interventional Distribution for one data sample
E_{i\sim p(i)}[Y=y|i,do\{T=t\}]
We can compute for a set of samples (i.e., code snippets) obtaining an ATE (average treatment effect)
E_{i\sim p(i)}[E[Y=y|i,do\{T=1\}]-E[Y=y|i,do\{T=0\}]]
For binary treatment (i.e., BuggyCode), we can derive an expected value expression.
Treatment (T=1) means FixedCode
NO Treatment (T=0) means BuggyCode
We can use the adjustment formula to compute or estimate causal effects from observational data (Pearl, et al., 2016)
Step 4: Validating Causal Process
How can we falsify graph-encoded assumptions?
Refuting Effect Estimates
Add Unobserved Common Cause
treatments
potential outcomes
confounders
\tau = p(y|do(T))
H
Unobserved Cause
\tau = p(y|do(T),H)
should be the same quantity
\tau
1. Modeling
2. Identification
4. Validation
3. Estimation
causal explanations
domain knowledge
input software data
exploratory analysis
Encode causal assumptions in a graph
Formulate a causal estimand
Structural Causal Graph
Math Expression
Compute a Causal Effect using an estimation method
Evaluate the robustness of estimated causal effect
Causal Estimation
\tau
After the doCode pipeline, we obtain our validated causal effect quantity!
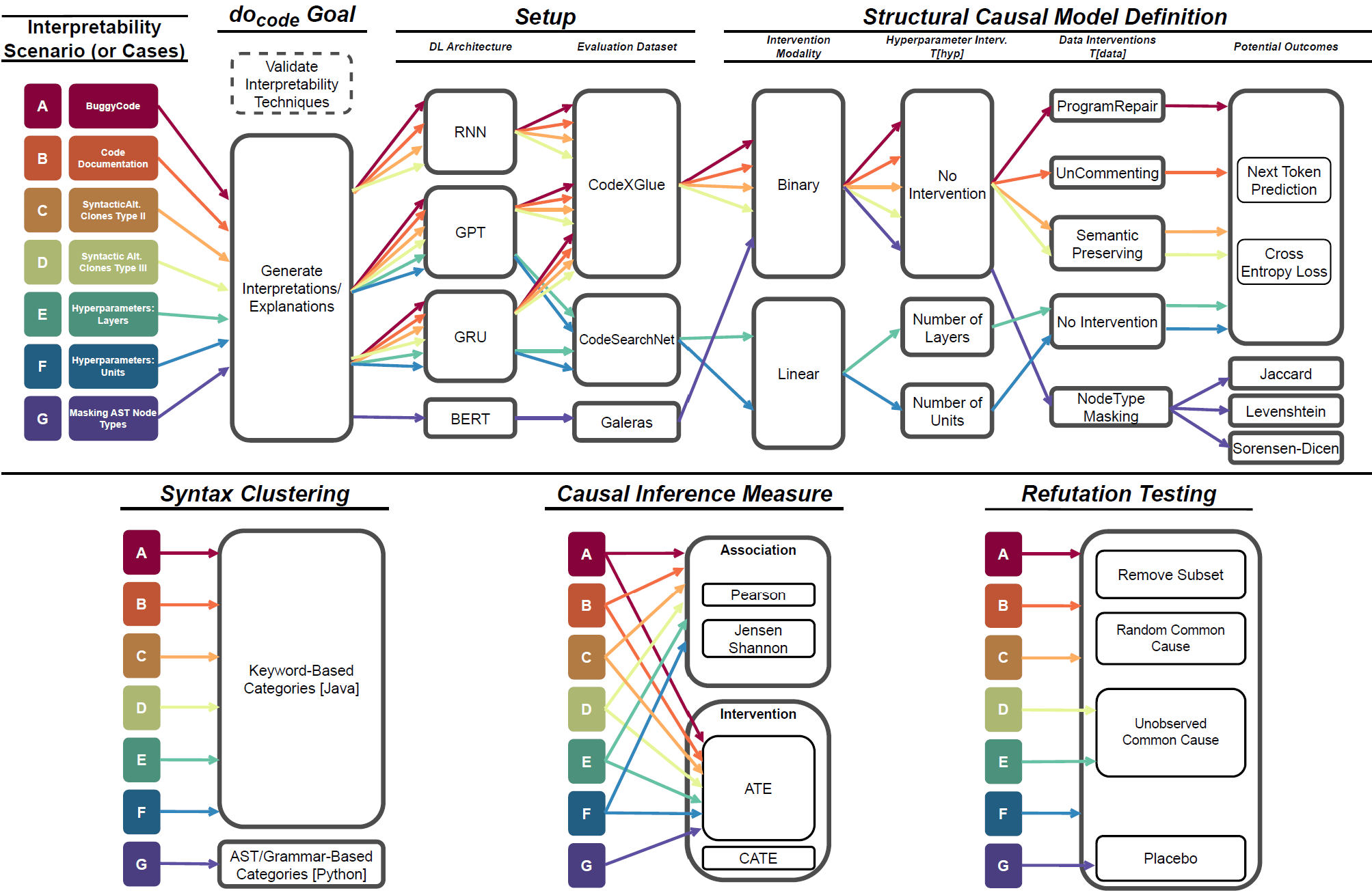
Case Study
Interpretability Scenarios in Software Engineering
We want to understand how code predictions react under different input data
(or hyperparameter tuning)
The study proposes 7 scenarios to demonstrate the efficacy and applicability of causal interpretability for code generation
Data-based interventions
Model-based interventions
Syntax Decomposition as Treatments
[case A] Buggy Code Impact
[case B] Inline Comments Impact
[case C|D] Code Clones Impact
[case E] # of Layers Impact
[case F] # of Units Impact
T_{data}
T_{params}
T_{syntax}
[case G] On encoder-only models
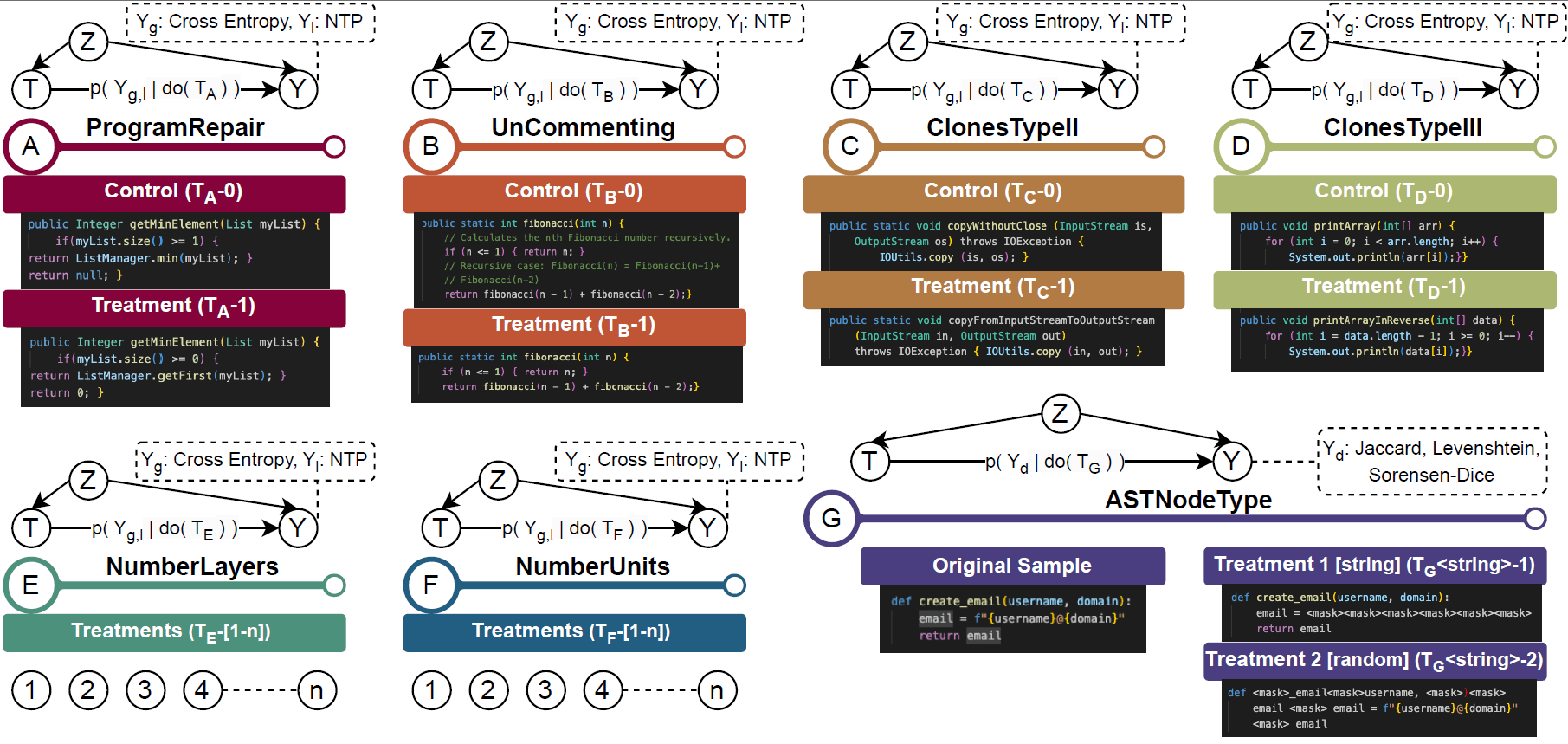
Seven permutations were proposed across causal dimensions,
but doCode allows for extending it
Experiment Setup for BuggyCode
Q = P(Y|do\{T\})
do_{code}
p(w_t|w_{1...t-1})
autoregressive
extract interpretability features
feasible snippets
output logits
causal explanations
Structural Causal Model (SCM)
To what extent does a (test) buggy sequence impact error learning or code prediction?
RNNs
GRUs
GPT2
Neural Code Models
Testbed: BuggyTB (Tufano, et al., 2019)
Training : CodeSearch Net
Associations vs. Intervention Results
treatments
potential outcomes
confounders
causal effect
Structural Causal Model
To what extent does a (test) buggy sequence impact error learning or code prediction?
Research Question
\tau
\tau = p(Y|T)
Level 1: Association
RNNs
GRUs
GPT2
0.730
0.230
0.670
Neural Code Model
Level 2: Intervention
\tau = p(Y|do\{T\})
-3.0e-4
-2.3e-5
-2.0e-4
Null Causal Effects after controlling for confounders
A summary of the most relevant implications and findings for SE practitioners
No strong evidence that buggy code, comments, or syntax changes in the context window influence/cause NCMs' performance
Information Content in the prompt affects (positively and negatively) code predictions
BERT-like NCMs do not entirely capture the node's information of Abstract Syntax Trees (ASTs)
[special] Prompt Engineering
[cases A, B, C, and D]
[case E and F]
T_{data}
T_{params}
T_{syntax}
T_{prompt}
[case G]
No strong evidence that minimal increments in the #layers or #units influence/cause NCMs' performance
Consolidation
Who benefits from Causal Interpretability?
Software Researchers
- Introducing rigorous and formal methods to understand, explain, and evaluate NCMs (Palacio, et al., 2023).
- Promoting the use of Causal Inference as a complementary framework for Empirical SE studies, e.g., "the why-type questions" (Palacio, et al., 2025).
Practitioners from Industry
- Providing recourse to practitioners who are negatively affected by predictions, e.g., NCMs generating buggy code without affecting accuracy (Palacio, et al., 2023; Rodriguez-Cardenas, et al. 2023).
- Vetting models to determine if they are suitable for deployment, e.g., different interpretability scenarios (Palacio, et al., 2023).
- Assessing if and when to trust model predictions by detecting confounding bias (Velasco, et al., 2023; Khati, et al., 2025).
doCode can provide a more transparent, robust, and explainable approach to DL4SE, allowing for a better understanding of the decision-making process of the model and facilitating more effective detection of confounding bias
\Phi
Conclusion
Gracias!
Thank you!
Repository
Profile
[ICSE25] Causal Interpretability for DL4SE
By David Nader Palacio
[ICSE25] Causal Interpretability for DL4SE
Discover innovative approaches to enhance the interpretability of deep learning in software engineering. Explore groundbreaking insights that promise to transform the field and foster a deeper understanding of complex models. Join us on this exciting journey!
