The Geometry of Domino Tilings
David Radcliffe
dradcliffe@gmail.com
Introduction
A domino is a 2x1 rectangular region in the plane.
Given a polygonal region P in the plane, we are interested in the following questions.
- Does P admit a tiling by dominoes?
- Is there an efficient algorithm to find a domino tiling of P, if one exists?
- In how many ways can P be tiled by dominoes?
- What is the "geometry" of the set of all domino tilings of P?
- Bullet One
- Bullet Two
- Bullet Three
Orienting the edges
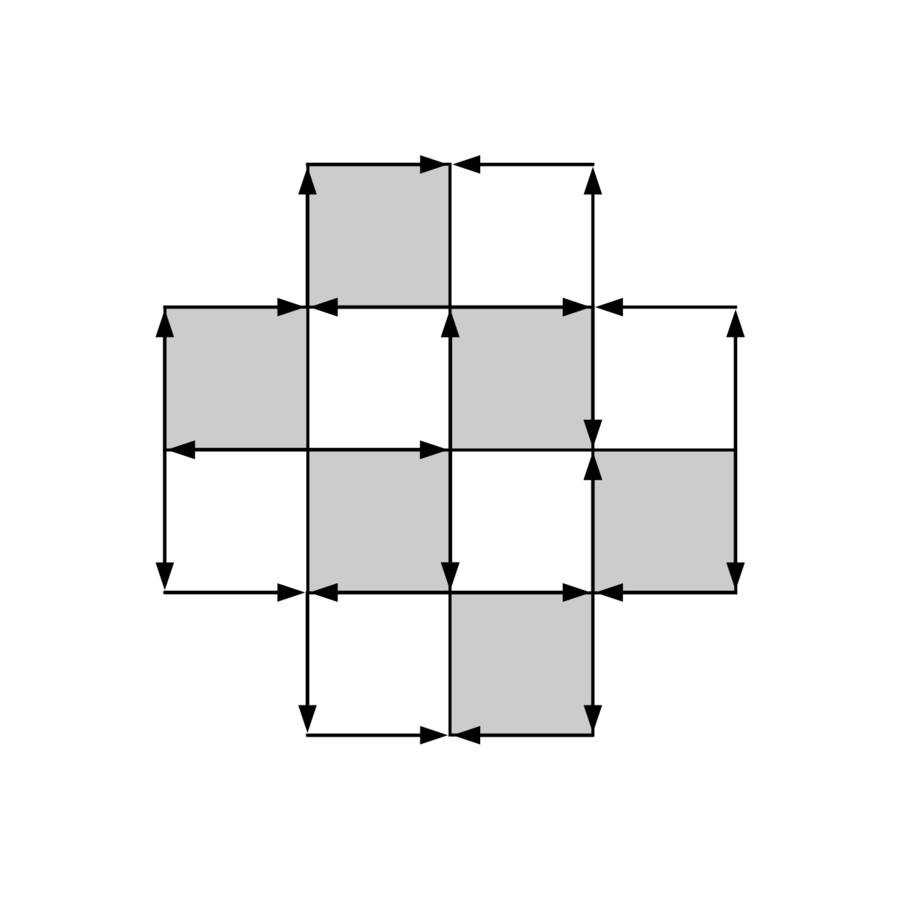
Boundary of a polygonal region
If a polygonal region is tiled by dominoes, then the "integral" around the boundary is zero.
The height function
A domino tiling determines a unique height function on the grid points, up to a constant.
Conversely, a valid height function determines a unique domino tiling.
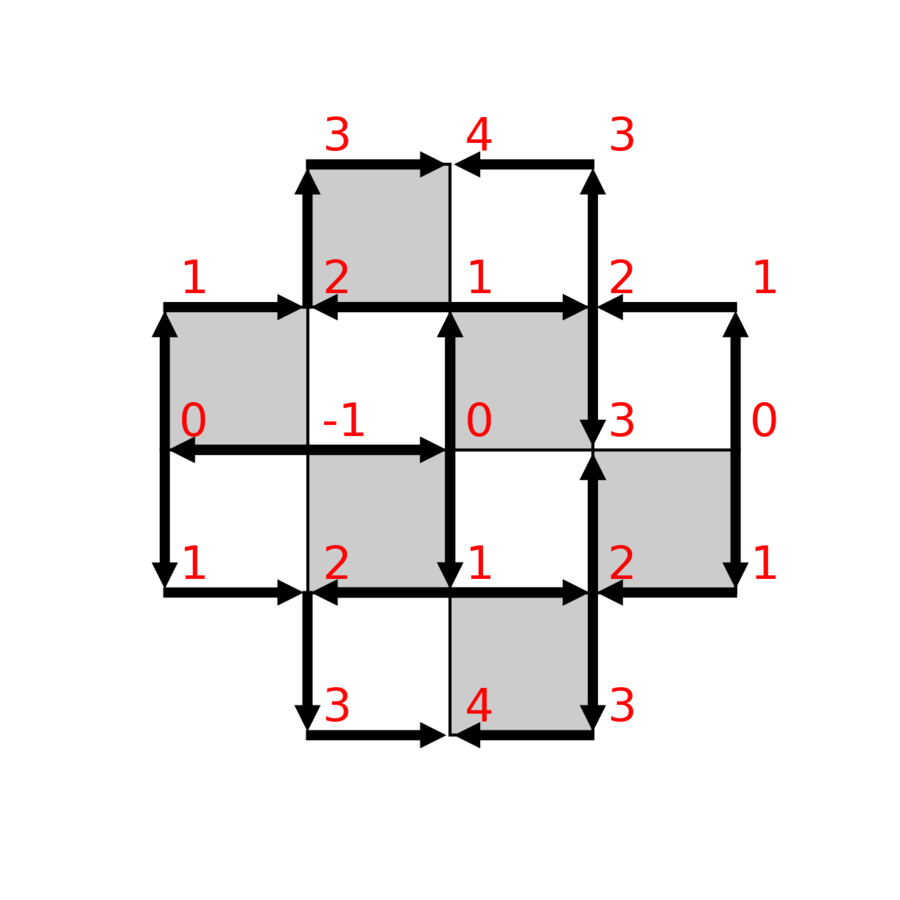
Properties of height functions
- The base point has height 0.
- For each directed edge uv on the boundary,
- For each directed edge uv in the interior,
h(v) - h(u) = 1.
h(v)−h(u)=1.
h(v) - h(u) \in \{-3, 1\}.
h(v)−h(u)∈{−3,1}.
There is a one-to-one correspondence between domino tilings and height functions.
Order properties of height functions
- The set of height functions on a polygonal region P forms a partially ordered set.
- The maximum or minimum of two height functions is also a height function.
- Therefore, the set of height functions on a polygonal region is a distributive lattice.
h_1 \leq h_ 2 \Longleftrightarrow \forall v:h_1(v) \le h_2(v)
h1≤h2⟺∀v:h1(v)≤h2(v)
(h_1 \vee h_2)(v)=\max\{h_1(v), h_2(v)\}
(h1∨h2)(v)=max{h1(v),h2(v)}
(h_1 \wedge h_2)(v) = \min\{h_1(v), h_2(v)\}
(h1∧h2)(v)=min{h1(v),h2(v)}
Local flips
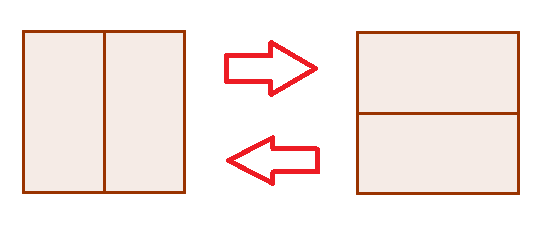
- A local flip is a 90 degree rotation of a 2x2 square formed by two adjacent dominoes.
- A local flip increases or decreases the height of the center of the square by 4, but does not change the heights of the other grid points.
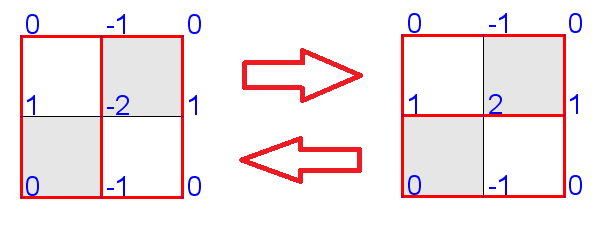
Local maxima and minima
- A local maximum (or minimum) is an interior grid point that is higher (or lower) than its neighbors.
- Local extrema occur at the center points of 2x2 blocks
- A local flip converts a local maximum to a local minimum, and vice versa.
Distance function
The distance between two height functions is
Theorem 1. Any two domino tilings can be connected by a sequence of local flips.
Theorem 2. The minimum number of flips required to transform one tiling to another is equal to the distance between the height functions.
d(h_1, h_2) = \dfrac14 \sum\limits_v |h_1(v) - h_2(v)|.
d(h1,h2)=41v∑∣h1(v)−h2(v)∣.
Highest domino tiling
\dfrac14 \sum\limits_v h(v) = \dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = 42
41v∑h(v)=21⋅(72+52+32+12)=42
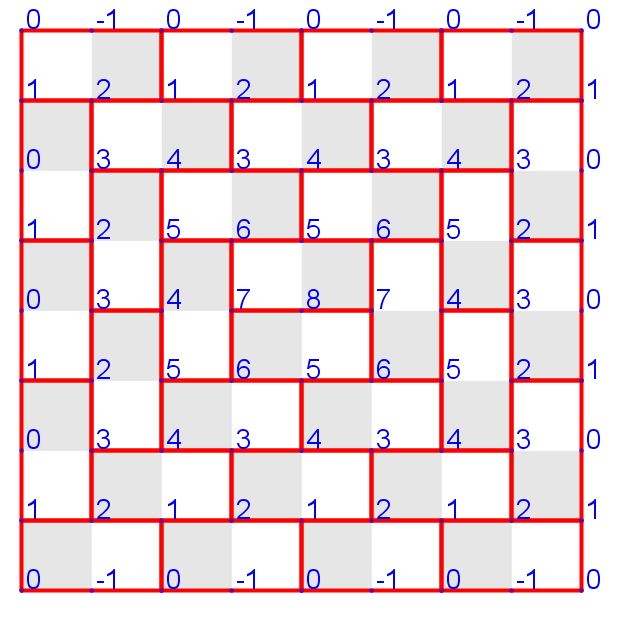
Lowest domino tiling
\dfrac14 \sum\limits_v h(v) = -\dfrac12 \cdot (7^2 + 5^2 + 3^2 + 1^2) = -42
41v∑h(v)=−21⋅(72+52+32+12)=−42
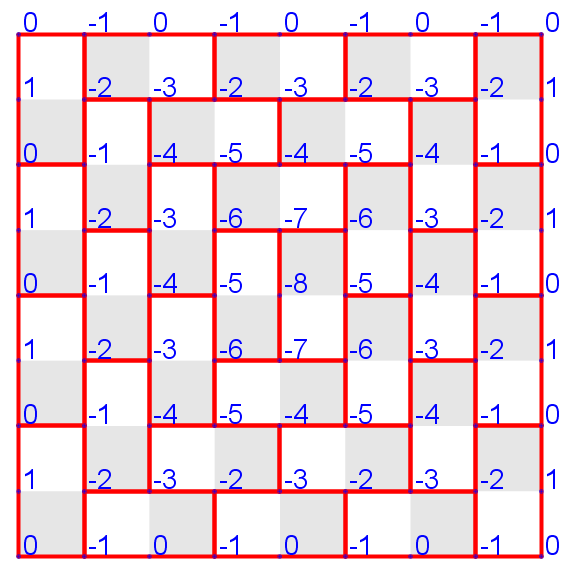
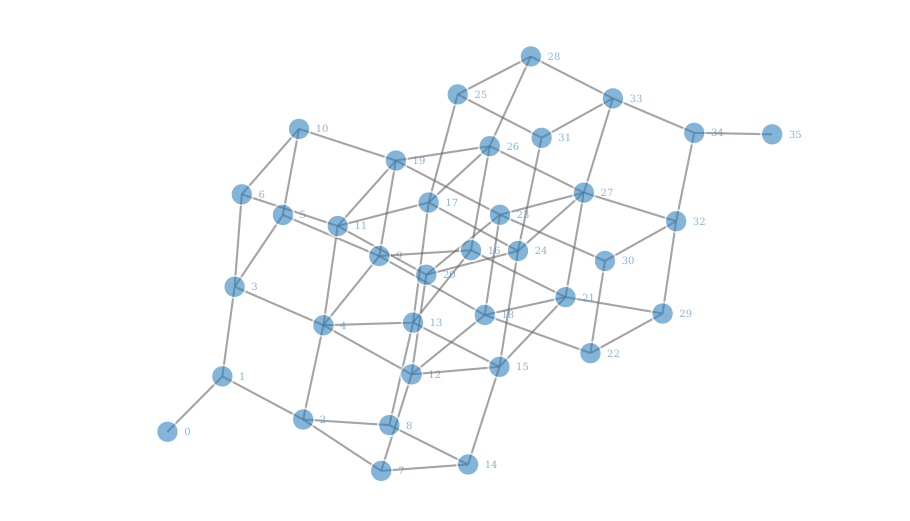
Visualizing the set of all domino tilings
The Geometry of Domino Tilings David Radcliffe dradcliffe@gmail.com
The Geometry of
By David Radcliffe
The Geometry of
- 1,246
