Matematik Projekt

Trigonometri

Teori

OBS: Teorien er ufuldstændig pga. noter osv. og meget af det er egentlig bare til mig selv

Pythagoras

a^2+b^2=c^2

a ​ 2 ​ ​ + b ​ 2 ​ ​ = c ​ 2 ​ ​

Areal af polygon

A=\frac{1}{4}\cdot n\cdot b^2\cdot\frac{cos(\frac{180^{\circ}}{n})}{sin(\frac{180^{\circ}}{n})}

A = \frac{​ 1 ​ ​}{​ 4 ​} \cdot n \cdot b ​ 2 ​ ​ \cdot \frac{​ c o s ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ n ​} ) ​ ​}{​ s i n ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ n ​} ) ​}

1/2 Appelsin

Sinusrelationerne

Det er her hvor mine noter går galt igen igen..

http://bevissamling.systime.dk/index.php?id=314

Cosinusrelationerne

Vinkelsumssætningen

Hvis man har to af vinklerne i en trekant, så kan man finde den sidste ved at trække summen af de to vinkler fra 180.

Retvinklede trekanter - cos, sin, tan

https://www.youtube.com/watch?v=IJoUu_b9Fgg

Enhedscirklen

Opgave 1

Den første opgave omhandler polygoner og trekanter, hvor man selv skal finde på sin egen polygon, men som skal være regulær. Vi skal herefter lave beregninger med denne polygon ved hjælp af trekanter.

a) Skitsér en regulær polygon

Det er en 12-sidet polygon og en side er 24

b) Triangulér polygon

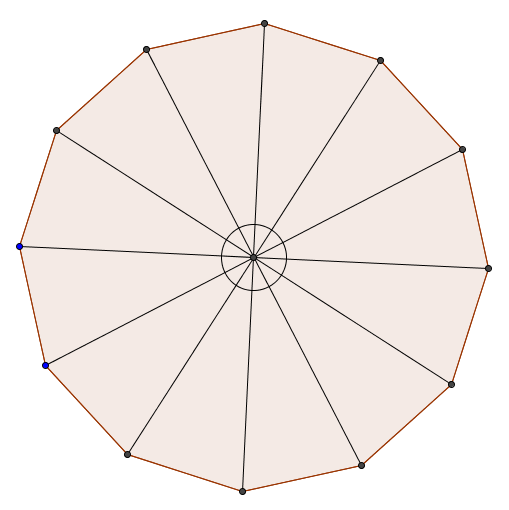
c) Udregn areal af polygon

Jeg har nu mit polygon delt op i vilkårlige trekanter. Jeg kan beregne arealet af disse trekanter ved hjælp af:

Indtil videre kender jeg kun længden på én side på hver trekant. Siden er 24, og jeg har valgt at kalde den for "b". Jeg mangler dog stadig, siden a og en vinkel C. Jeg finder først ud af den manglende vinkel.

Den samlede vinkelsum for den vinkel, som er tættest mod polygonets centrum af hver trekant, er 360 grader. Derfor kan jeg også godt finde den vinkel, som er tættest mod polygonets centrum, da jeg ved, at der er 12 trekanter inden i polygonet, og som jeg desuden har valgt at kalde for "B".

Hver trekant har altså en vinkel B, som er 30 grader. I et regulært polygon er alle trekanterne ligebenet, og da vinkelsummen for en trekant er 180 grader, så må hver af de resterende vinkler være:

T=\frac{1}{2}\cdot a\cdot b\cdot sin(C)

T = \frac{​ 1 ​ ​}{​ 2 ​} \cdot a \cdot b \cdot s i n (C)

B=\frac{360}{12}=30^{\circ}

B = \frac{​ 3 6 0 ​ ​}{​ 1 2 ​} = 3 0 ​ \circ ​ ​

\frac{180^{\circ}-30^{\circ}}{2}=75^{\circ}

\frac{​ 1 8 0 ​ \circ ​ ​ - 3 0 ​ \circ ​ ​ ​ ​}{​ 2 ​} = 7 5 ​ \circ ​ ​

c) Udregn areal af polygon

b = 24

c) Udregn areal af polygon

Jeg kender nu vinkel A og C og mangler kun siden a. Siden a kan jeg finde ved hjælp af sinusrelationerne, da jeg kender vinkel A, vinkel B og siden b. Jeg isolerer a ved hjælp af Maple.

Jeg kan nu beregne arealet af én af trekanterne i polygonet, og derefter gange det med antallet af trekanter. Produktet er det samme som arealet af hele polygonet.

\frac{a}{sin(A)}=\frac{b}{sin(B)}=\frac{c}{sin(C)}

\frac{​ a ​ ​}{​ s i n ( A ) ​} = \frac{​ b ​ ​}{​ s i n ( B ) ​} = \frac{​ c ​ ​}{​ s i n ( C ) ​}

\frac{a}{sin(75)}=\frac{24}{sin(30)}

\frac{​ a ​ ​}{​ s i n ( 7 5 ) ​} = \frac{​ 2 4 ​ ​}{​ s i n ( 3 0 ) ​}

a=46,36443968

a = 46, 36443968

T=\frac{1}{2}\cdot a\cdot b\cdot sin(C)

T = \frac{​ 1 ​ ​}{​ 2 ​} \cdot a \cdot b \cdot s i n (C)

T_{trekant}=\frac{1}{2}\cdot 46,36443968\cdot 24\cdot sin(75)=537,4153165

T ​ t r e k a n t ​ ​ = \frac{​ 1 ​ ​}{​ 2 ​} \cdot 46, 36443968 \cdot 24 \cdot s i n (75) = 537, 4153165

T_{polygon}=537.4153165\cdot 12=6448,983798

T ​ p o l y g o n ​ ​ = 537.4153165 \cdot 12 = 6448, 983798

d) Areal ved hjælp af formel

Jeg skal finde arealet af polygonet ved hjælp af en formel, som kan findes på side 44 i Mat112. Formlen ser såldes ud:

Lille "n" står for antal sider polygonet har, og "b" er sidelængden.

A=\frac{1}{4}\cdot n\cdot b^2\cdot\frac{cos(\frac{180^{\circ}}{n})}{sin(\frac{180^{\circ}}{n})}

A = \frac{​ 1 ​ ​}{​ 4 ​} \cdot n \cdot b ​ 2 ​ ​ \cdot \frac{​ c o s ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ n ​} ) ​ ​}{​ s i n ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ n ​} ) ​}

A=\frac{1}{4}\cdot 12\cdot 24^2\cdot\frac{cos(\frac{180^{\circ}}{12})}{sin(\frac{180^{\circ}}{12})}=6448,983796

A = \frac{​ 1 ​ ​}{​ 4 ​} \cdot 12 \cdot 2 4 ​ 2 ​ ​ \cdot \frac{​ c o s ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ 1 2 ​} ) ​ ​}{​ s i n ( \frac{​ 1 8 0 ​ \circ ​ ​ ​ ​}{​ 1 2 ​} ) ​} = 6448, 983796

e) Sammenlign resultater

Med trigonometri fik jeg resultatet til 6448,983798 og med formel, 6448,983796. Resultaterne er sådan set næsten det samme. Der er dog forskel på det sidste decimal, men det er sikkert fordi, Maple enten har rundet op eller ned ved opgaven uden formel.

Opgave 2

Anden opgave handler om en festlig fætter som står en vis afstand fra et skilt. Man skal bl.a. beregne synsvinklen fra fætteren til skiltet afhængigt af afstanden, og man skal vurdere, hvor når skiltet er læseligt, afhængigt af hvad der står på skiltet.

a) Skitse af situation

1,3

12 - fra skilt til fætter

1,65 høj til øjne

b) Person A - Udregn synsvinkel

1,3

1,65 høj til øjne

GRØN

RØD

Hele trekant = PINK

b) Person A - Udregn synsvinkel

For at kunne beregne synsvinklen, har jeg valgt at lave én stor retvinklet trekant - referer til den som PINK. Trekanten er delt op i to trekanter, hvor den ene trekant er synsvinklen, som også er en vilkårlig trekant - den kalder jeg for GRØN. Den anden er en retvinklet trekant, som jeg kalder for RØD.

PINK har en grundlinje på 12, som jeg kalder "b". Den har også en vinkel på 90 grader, som jeg kalder for "C". Da jeg kender højden på manden, skiltstangens højde og selve skiltets højde, så kan jeg beregne siden "b":

Da det er en retvinklet trekant så gælder: - vi kan altså beregne den vinkel som er tættest mod fætteren, "B". Jeg bruger Maple til de fleste udregninger.

b_{PINK}=3-1,65+1,3=2,65

b ​ P I N K ​ ​ = 3 - 1, 65 + 1, 3 = 2, 65

tan(v)=\frac{mod}{hos}

t a n (v) = \frac{​ m o d ​ ​}{​ h o s ​}

solve(tan(B)=\frac{2,65}{12},B)

s o l v e (t a n (B) = \frac{​ 2 , 6 5 ​ ​}{​ 1 2 ​}, B)

B_{PINK} = 12,45295279^{\circ}

B ​ P I N K ​ ​ = 12, 4529527 9 ​ \circ ​ ​

b) Person A - Udregn synsvinkel

1,3

a = 12

1,65 høj til øjne

GRØN

RØD

Hele trekant = PINK

b = 2,65

B = 12,45^{\circ}

B = 12, 4 5 ​ \circ ​ ​

C = 90^{\circ}

C = 9 0 ​ \circ ​ ​

b) Person A - Udregn synsvinkel

Samme princip kan jeg nu gøre med RØD. Jeg kender dog ikke RØD's side b, men jeg kan regne den ud, da jeg har skiltstangens højde og fætterens højde:

Jeg kan nu regne vinklen tættest mod fætteren ud for RØD:

Endeligt kan jeg regne synsvinklen ud, som også er det samme som vinkel "B" for GRØN:

Synsvinklen er altså 6,034166060 grader.

b_{ROD}=3-1,65=1,35

b ​ R O D ​ ​ = 3 - 1, 65 = 1, 35

tan(v)=\frac{mod}{hos}

t a n (v) = \frac{​ m o d ​ ​}{​ h o s ​}

solve(tan(B)=\frac{1,35}{12},B)

s o l v e (t a n (B) = \frac{​ 1 , 3 5 ​ ​}{​ 1 2 ​}, B)

B_{ROD} = 6,418786730^{\circ}

B ​ R O D ​ ​ = 6, 41878673 0 ​ \circ ​ ​

B_{GRON} = B_{PINK}-B_{ROD}

B ​ G R O N ​ ​ = B ​ P I N K ​ ​ - B ​ R O D ​ ​

B_{GRON} = 12,45295279-6,418786730=6,034166060^{\circ}

B ​ G R O N ​ ​ = 12, 45295279 - 6, 418786730 = 6, 03416606 0 ​ \circ ​ ​

1,3

12 - fra skilt til fætter

1,65 høj til øjne

b) Person A - Udregn synsvinkel

GRØN

B = 6,03^{\circ}

B = 6, 0 3 ​ \circ ​ ​

1,3

x - fra skilt til fætter

1,65 høj til øjne

b) Person A - Funktion(afstand)

c) Person A - Funktion(afstand)

For at kunne undersøge hvordan synsvinklen ændrer sig når afstanden ændrer sig, har jeg valgt at lave en funktion for dette. Funktionen er lavet ud fra de forrige beregninger, bare hvor jeg har erstattet afstanden 12 med x:

Hvis jeg sætter 12 ind som x, så får jeg en vinkel på 6,034166064 - det passer meget godt med mit forrige resultat af vinklen, hvor afstanden også var på 12.

Når jeg prøver at sætte 24 ind som x, så får jeg en vinkel på 3,081390351 - det passer også meget godt, at vinklen bliver mindre, jo længere væk man er.

f(x)=tan^{-1}(\frac{2,65}{x})-tan^{-1}(\frac{1,35}{x})

f (x) = t a n ​ - 1 ​ ​ (\frac{​ 2 , 6 5 ​ ​}{​ x ​}) - t a n ​ - 1 ​ ​ (\frac{​ 1 , 3 5 ​ ​}{​ x ​})

b) Person B - Udregn synsvinkel

1,3

a = 12

1,65 høj til øjne

GRØN

RØD

Hele trekant = PINK

b = 1,35

C = 90^{\circ}

C = 9 0 ​ \circ ​ ​

b) Person B - Udregn synsvinkel

Da rød er en retvinklet trekant og jeg kender a og b fra forrige opgave med person A, så kender jeg bruge pythagoras til at regne hypotenusen for RØD ud.

Nu har jeg længden af siden c for RØD. Det betyder, at jeg også har længden af siden a for GRØN.

a^2+b^2=c^2

a ​ 2 ​ ​ + b ​ 2 ​ ​ = c ​ 2 ​ ​

c^2=12^2+1,35^2=145,8225

c ​ 2 ​ ​ = 1 2 ​ 2 ​ ​ + 1, 3 5 ​ 2 ​ ​ = 145, 8225

c=\sqrt{145,8225}=12,07569874

c = \sqrt ​ 145, 8225 ​ ​ ​ = 12, 07569874

b) Person B - Udregn synsvinkel

a = 12

b = 1,35

C = 90^{\circ}

C = 9 0 ​ \circ ​ ​

a = 12,08

b = 1,3

b) Person B - Udregn synsvinkel

Som man kan se på forrige billede, så mangler jeg stadig enten en vinkel eller en side for at beregne med cosinusrelationerne for GRØN. Jeg ved fra før at: , så jeg kan beregne vinkel A for RØD, og derefter trække 180 fra for at få vinkel C for GRØN. Jeg kan trække 180 fra, da der er 180 grader.

Nu kan jeg bruge cosinusrelationerne til at beregne siden c for GRØN.

Dette giver mig 2 resultater, men da det er en afstand valgte jeg det positive tal.

A_{ROD}=83,58121322^{\circ}

A ​ R O D ​ ​ = 83, 5812132 2 ​ \circ ​ ​

tan(v)=\frac{mod}{hos}

t a n (v) = \frac{​ m o d ​ ​}{​ h o s ​}

solve(tan(A)=\frac{12}{1,35},A)

s o l v e (t a n (A) = \frac{​ 1 2 ​ ​}{​ 1 , 3 5 ​}, A)

C_{GRON}=180-83,58121322=96,41878678^{\circ}

C ​ G R O N ​ ​ = 180 - 83, 58121322 = 96, 4187867 8 ​ \circ ​ ​

cos(C)=\frac{a^2+b^2-c^2}{2ab}

c o s (C) = \frac{​ a ​ 2 ​ ​ + b ​ 2 ​ ​ - c ​ 2 ​ ​ ​ ​}{​ 2 a b ​}

solve(cos(96,41878678)=\frac{12,07569874^2+1,3^2-c^2}{2\cdot 12,07569874\cdot 1,3},c)

s o l v e (c o s (96, 41878678) = \frac{​ 1 2 , 0 7 5 6 9 8 7 4 ​ 2 ​ ​ + 1 , 3 ​ 2 ​ ​ - c ​ 2 ​ ​ ​ ​}{​ 2 \cdot 1 2 , 0 7 5 6 9 8 7 4 \cdot 1 , 3 ​}, c)

c = 12,28912121

c = 12, 28912121

b) Person B - Udregn synsvinkel

a = 12,08

b = 1,3

C = 96,42^{\circ}

C = 96, 4 2 ​ \circ ​ ​

c = 12,23

b) Person B - Udregn synsvinkel

Jeg har nu alle siderne på GRØN. Jeg kan nu igen bruge cosinusrelationerne, men til vinklen B.

Synsvinklen er altså 6,034165984 grader, som næsten er det samme som Person A, der fik 6,034166060 grader.

cos(B)=\frac{a^2+c^2-b^2}{2ac}

c o s (B) = \frac{​ a ​ 2 ​ ​ + c ​ 2 ​ ​ - b ​ 2 ​ ​ ​ ​}{​ 2 a c ​}

solve(cos(B)=\frac{12,07569874^2+12,28912121^2-1,3^2}{2\cdot 12,07569874\cdot 12,28912121}, B)

s o l v e (c o s (B) = \frac{​ 1 2 , 0 7 5 6 9 8 7 4 ​ 2 ​ ​ + 1 2 , 2 8 9 1 2 1 2 1 ​ 2 ​ ​ - 1 , 3 ​ 2 ​ ​ ​ ​}{​ 2 \cdot 1 2 , 0 7 5 6 9 8 7 4 \cdot 1 2 , 2 8 9 1 2 1 2 1 ​}, B)

B = 6,034165984

B = 6, 034165984

c) Person B - Funktion(afstand)

For at kunne undersøge hvordan synsvinklen ændrer sig når afstanden ændrer sig, har jeg valgt at lave en funktion for dette. Funktionen er lavet ud fra processen af de forrige beregninger. Det er lidt svært at forklare hvordan jeg helt præcist laver funktionen, så derfor prøver jeg at vise processen via Maple. Det er dog værd at nævne at jeg erstatter afstanden 12 (a) med x, da det ligger til grund for min funktion. Her er filen til Maple:

https://www.dropbox.com/s/zn3mxt9y4r45ctl/Person%20B%20-%20Funktion.mw?dl=0

d) Ovejelser om skilt

Jeg har valgt, at min afstand til skiltet skal være 12 meter lang, og der skal stå "OBS: Løverne kan flyve" på skiltet. Synsvinklen til skiltet skal være minimum 1 grad. Zoo skal altså derfor lave om på skiltets højde, for at opfylde kravet, da Zoo ikke kan ændre på afstanden.

Matematik Projekt

Trigonometri

Teori

Pythagoras

Areal af polygon

1/2 Appelsin

1/2 Appelsin

Sinusrelationerne

Cosinusrelationerne

Cosinusrelationerne

Cosinusrelationerne

Vinkelsumssætningen

Retvinklede trekanter - cos, sin, tan

Enhedscirklen

Enhedscirklen

Opgave 1

a) Skitsér en regulær polygon

b) Triangulér polygon

c) Udregn areal af polygon

c) Udregn areal af polygon

c) Udregn areal af polygon

d) Areal ved hjælp af formel

e) Sammenlign resultater

Opgave 2

a) Skitse af situation

b) Person A - Udregn synsvinkel

b) Person A - Udregn synsvinkel

b) Person A - Udregn synsvinkel

b) Person A - Udregn synsvinkel

b) Person A - Udregn synsvinkel

b) Person A - Funktion(afstand)

c) Person A - Funktion(afstand)

b) Person B - Udregn synsvinkel

b) Person B - Udregn synsvinkel

b) Person B - Udregn synsvinkel

b) Person B - Udregn synsvinkel

b) Person B - Udregn synsvinkel

b) Person B - Udregn synsvinkel

c) Person B - Funktion(afstand)

d) Ovejelser om skilt

Matematik Projekt - Trigonometri

More from deam