Options From Example Trajectories
Zang 09 Paper by Denis, Emily
Outline
- Why you should care
- Subproblems+Options
- Analysis
- Experiments
Definitions
- SMDP M = (S, A, P, R, gamma)
- State Abstractions
- Up Projections g:S[F]→S[ ̃F]
- Down Projections h:S[ ̃F]→
- Trajectory T
- Subproblem (M, F, A, w)
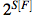

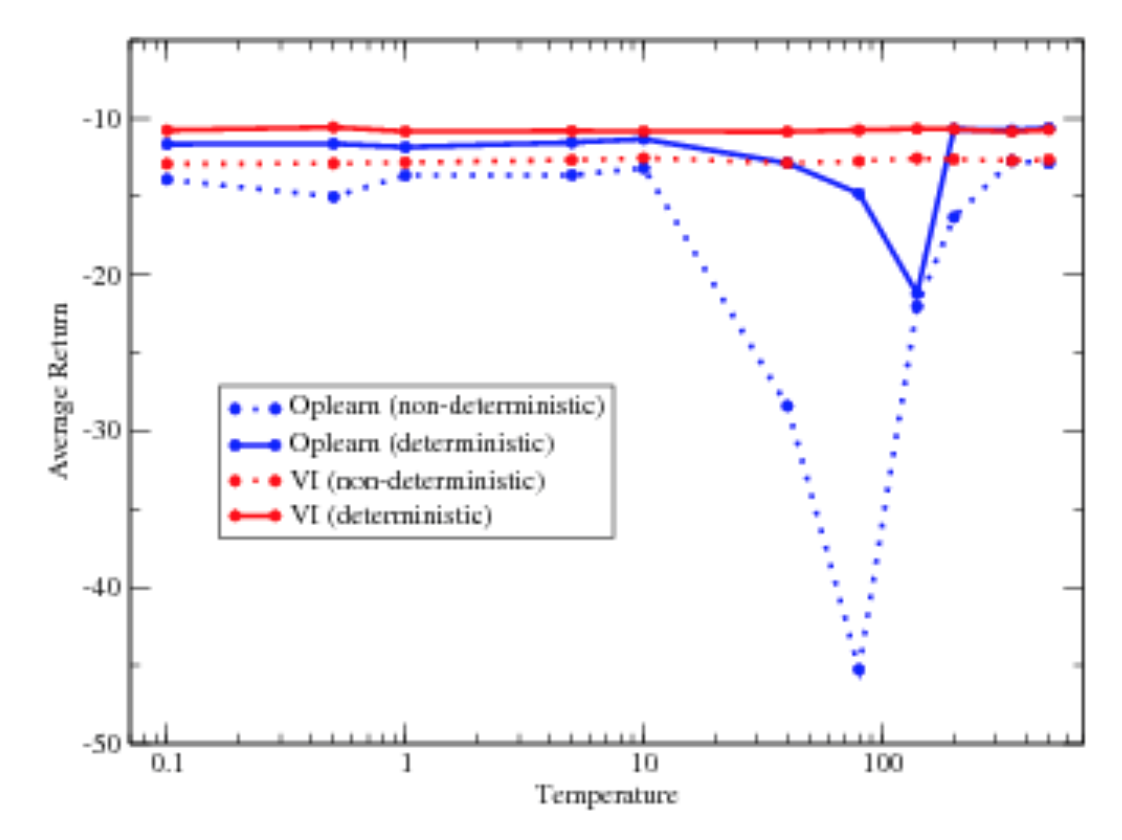
Equations
Subproblems
- What are subproblems?
- How do we get them?
- Why are they significant?

What makes a good Subproblem?
-
Size: encapsulates a significant chunk of the overall problem.
-
Frequency: subproblem arises frequently.
-
Abstraction: the greater the abstraction the faster we can solve the subproblem.
Recursing
- Original problem: SMDP passed in. Base problem: SMDP called recursively. Msub: R, transitions?
- IF Msub Solved -> Msub Becomes Option. A U S{o}
- Solving V(s), T(s). Prob = 1, Discount = T(s)
- Suffix Tree generation for common actions
Example:
- Given ENNNPWWWWD and that NN is common action
- ENNNPWWWWD - expand until state abstraction broken
- Goal is state prior to pickup-action.
- Extend backwards in time out of state abstraction:
- ENNN. Assign this to var X. New string: XPWWWWD
Analysis
- Requirements:
- model
- near-optimal trajectories
- Best for problems where different subproblems require different features
- 3D Flying vs pole balancing
- O(T^2) cost for best subproblem. And T < N!
- Works in deterministic & better in non-deterministic
Trajectory length is the culprit
Text
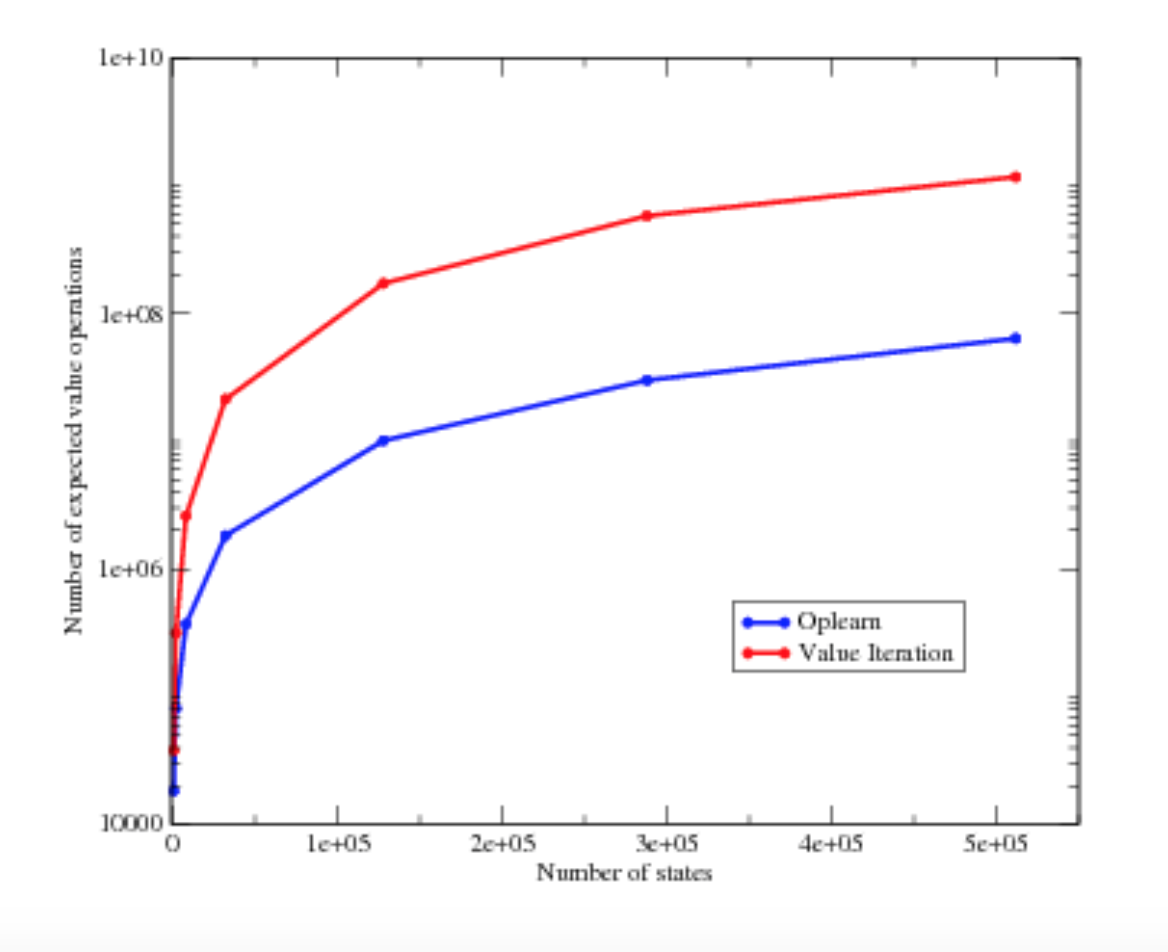
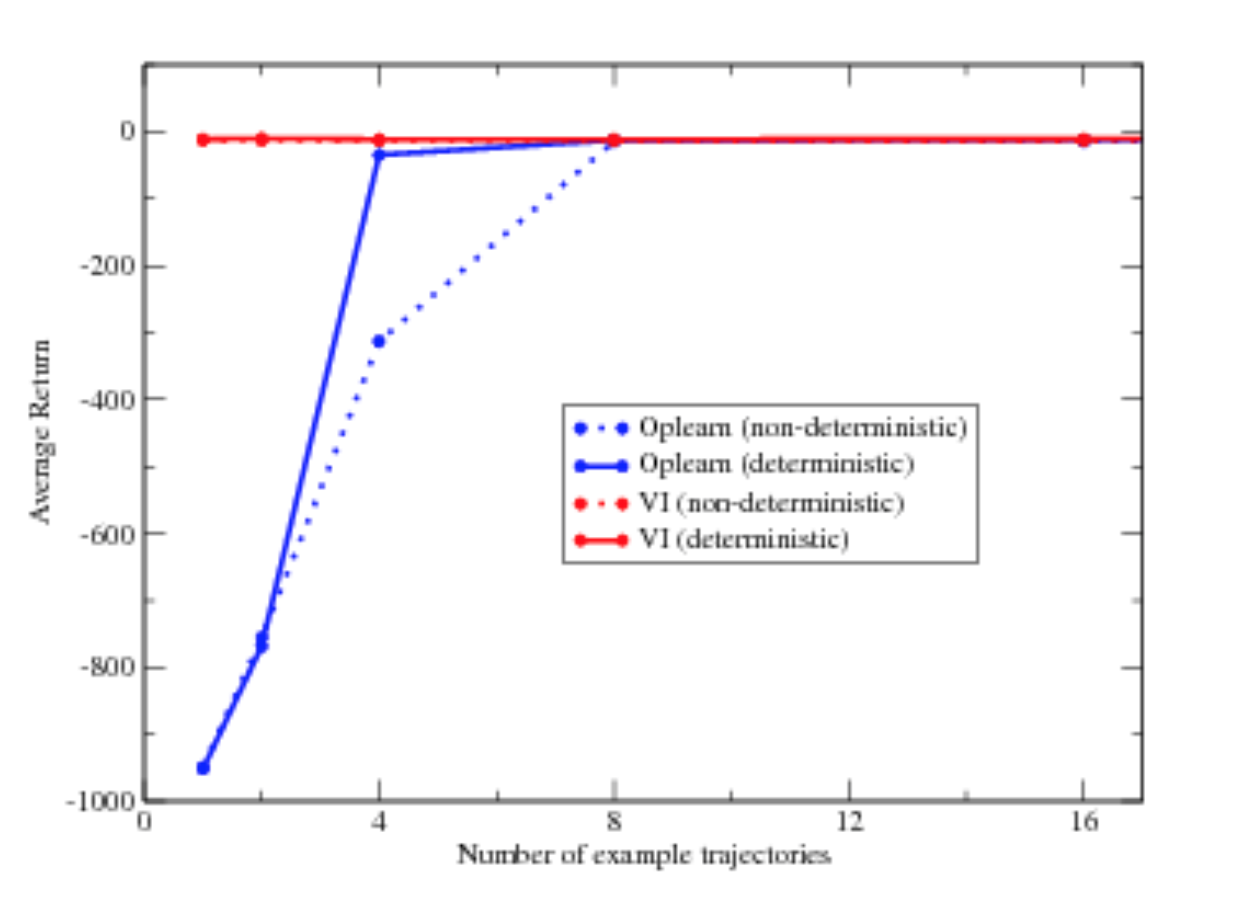
Robustness
Handles noise well.
But, remember that you need to see all actions.
Experiments
- Bad Problems
- Taxi
- Wars
Pole Balancing
Taxi
-
Taxi() 4-8 Ts
-
PickupPassenger()
-
Navigate()
-
-


Wargus
~15 Ts
- Idle
- GoToGoldMine
- GotoWoods,
- Chop
- Mine
- BuildBlackSmith
- TrainGrunt
Army size: 4
OpLearn: 2 mil
VI: 20 mil
Army Size: 8
OpLearn: 3 mil
VI: 80 mil
Take-Aways
- Recursively find sub-problems
- To reduce state space + computations
- To reduce trajectories needed
- To reduce state space + computations
Options
By dpeskov
Options
- 780



