Policy Gradient (PG) +Parameter-Based Exploration (PE)        = PGPE

PG

• Value Function
• Gradient Ascent
• Pros: Easy to incorporate domain knowledge, less parameters, model-free
• Problem: Stochasticity in policy
  • High variance in noisy sample.
  • Variance increases along T
• Example: Williams '92 REINFORCE

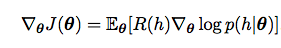
PGPE

• Linear, Deterministic Policy
• Parameters sampled from prior distribution at START of trajectory.  Draws with hyperparameter ⍴.   
• Pros:
  1. solves policy initialization problem
  2. reduces variance (single sample, T)
• Issue: still variance...
• Example: Sehnke '08 (and Peters)

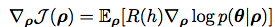
Baseline

Types

• Guess - (Jellybeans)
• Zero Rule - (Titanic) 
• For RL, the obvious baseline is Average Reward
• Optimal baseline = minimize variance +      not introduce bias

Literature

• Williams '92                (variance growth cubical along h and quadratically along with reward.            can only be single number in episodic REINFORCE)
• Greensmith '04                  (basis function challenge)
• Peters '08                       (separate baseline for each coefficient gradient )
• Zhao '11                               (optimal baseline PGPE > optimal REINFORCE)

Their baseline

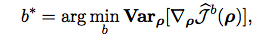
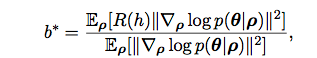
Take over Sample D

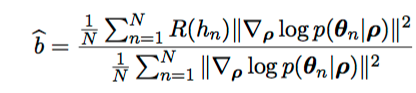
Solve

What's interesting?

1. Accounts for correlation
2. Nothing much in this paper

Variance Regularization

• Why
• How
• Math

Why Regularize Variance?

• Maximize reward while reducing variance in policy gradient

• Makes changes to ρ smoother

• Can still subtract baseline from R(h) for best results

New Objective Function

1.

2.

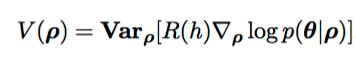
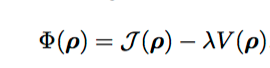
Additional Equations

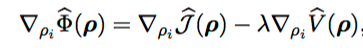
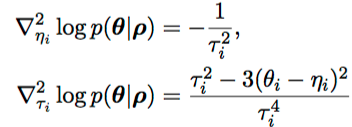
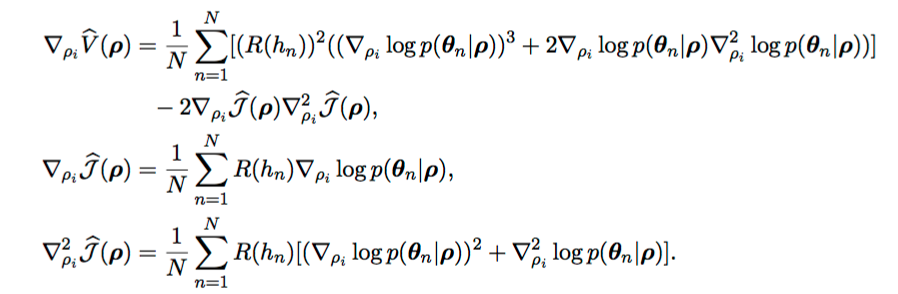
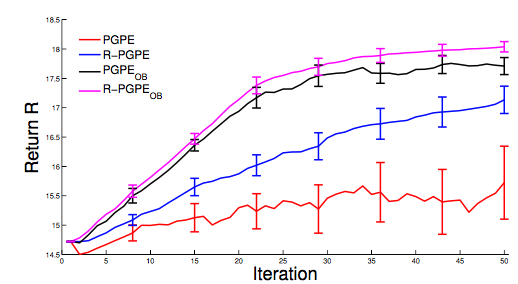
Experiments

Performance

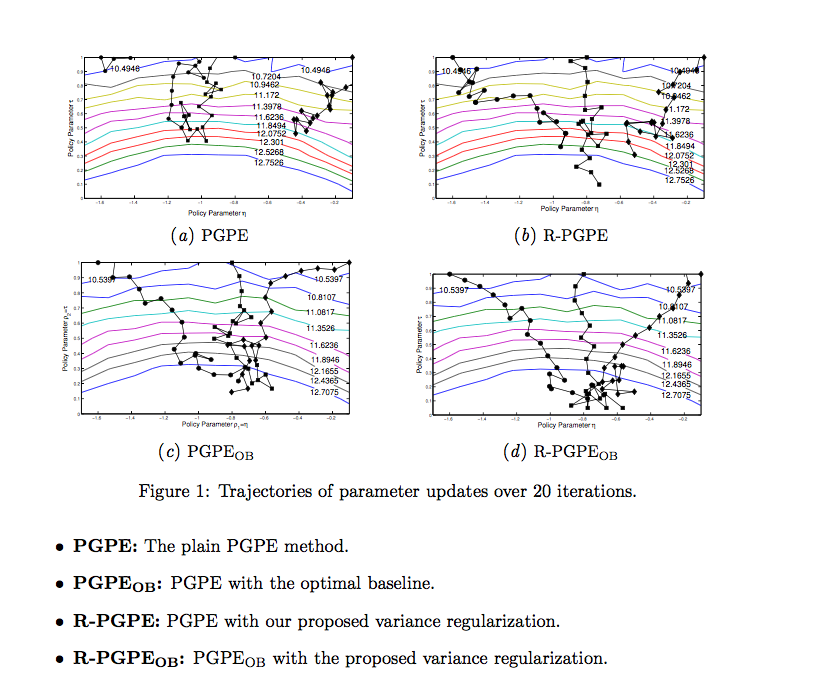
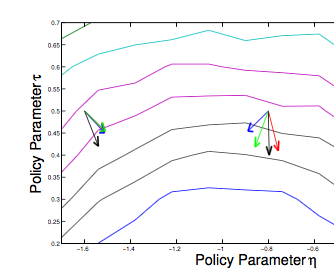
Performance Continued

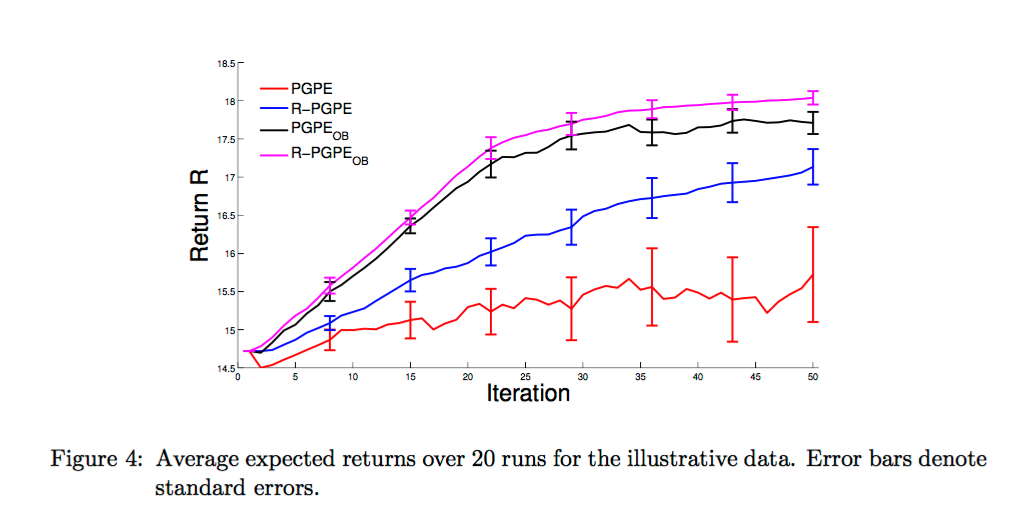
Mountain Car

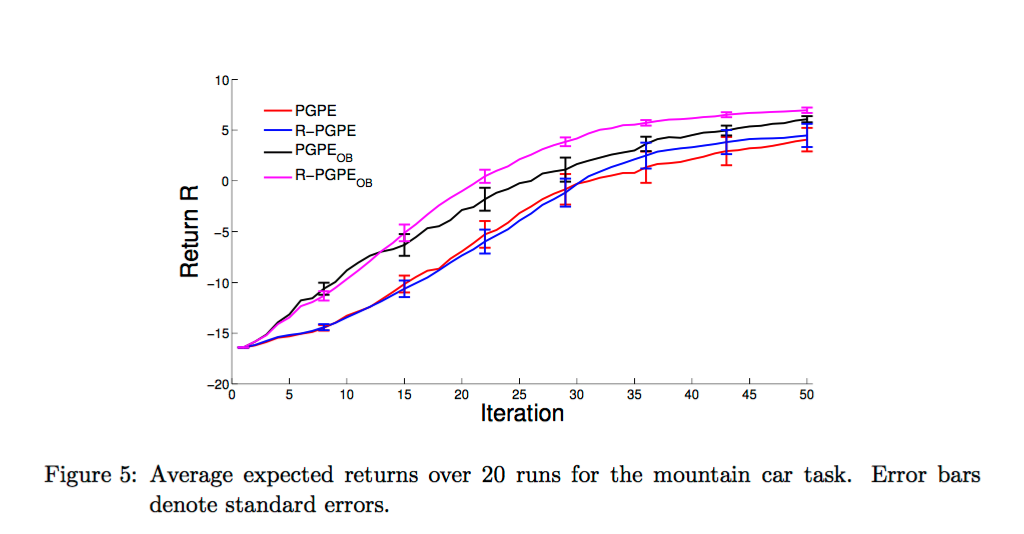
Stroke Rendering

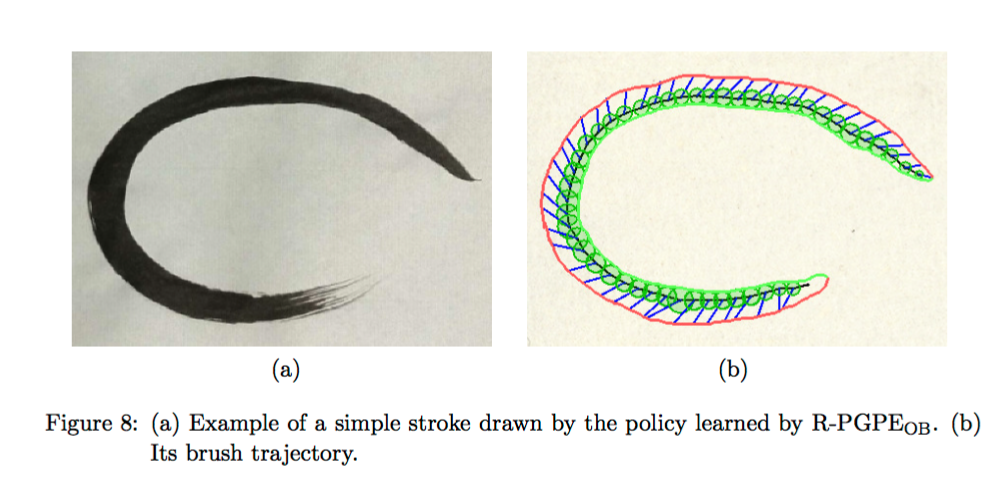
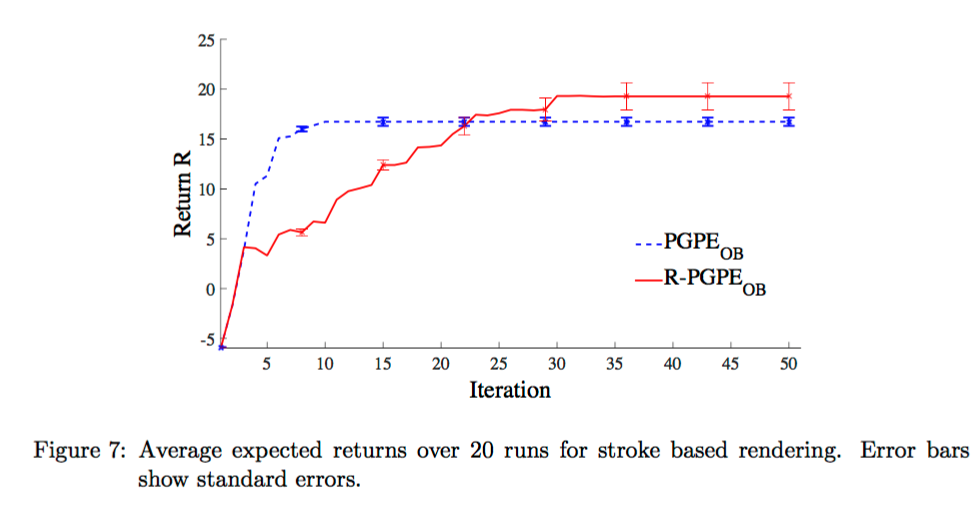
More Examples