Matrix Factorization Techniques for Recommender Systems
Yehuda Koren, Robert Bell,
and Chris Volinsky
IEEE Computer'09
Recommender Systems
- Modern Recommender Systems:
Analyze patterns of user interest in products to provide personalized recommendations that suit a user’s taste. - Strategies:
Content Filtering and Collaborative Filtering
Content Filtering
- Create a profile for each user or product to characterize its nature.
e.g. Movie: genre, actors, box office popularity, etc.
User: demographic info. - Require gathering external info that might not be available or easy to collect.
- Realization:
Music Genome Project in Pandora.com
Collaborative Filtering
- Relies only on past user behavior.
(Mostly the previous transactions or product ratings) - Domain free comparing to Content Filtering.
-
Cold start problem:
Difficult to address new products and users. - 2 primary areas of collaborative filtering:
Neighborhood methods and Latent factor models
Neighborhood Methods
- Centered on computing the relationships
between items or between users. - User-oriented and Item-oriented
- A user's neighbors are other users that tend to make similar ratings on the same product.
- A product’s neighbors are other products that tend
to get similar ratings when rated by the same user.
Latent Factor Models
- Map users and items to the same vector space with certain latent features.
- Latent features can even include uninterpretable ones.
- A user's preference can be modeled by the
dot product of the movie’s and user’s latent factor vector.
Neutral on this 2 dims.
This item/user may not be well represented by this 2 dims.
Matrix Factorization Model
- The most successful realizations of latent factor models.
- Good accuracy, scalability, and flexibility
- Can apply both explicit feedbacks (sparse) and implicit feedbacks (dense)
Matrix Factorization Model
- The user-item interactions are modeled by
where - Other methods:
(1) Single Value Decomposition (SVD):
Problem: Sparseness of rating matrix
- Conventional SVD is undefined when knowledge about the matrix is incomplete.
- Carelessly addressing only the relatively few known entries is highly prone to overfitting.
Matrix Factorization Model
- Other methods:
(2) Imputation (Statistics):
Problem: Sparseness of rating matrix
- May significantly increase the amount of data
- Inaccurate imputation might distort the data considerably
Matrix Factorization Model
- Proposed Method:
Model directly the observed ratings only, while avoiding overfitting through a regularized model.
Learning Algorithms
-
Stochastic Gradient Descent (SGD)
Initialize user and item latent factor vectors randomly
for t = 0, 1, ..., T
(1) Randomly pick 1 known rating
(2) Calculate Residual
(3) Update user and item latent vector by gradient
- Pros: Efficient Execution
r_{ui}
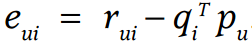
Learning Algorithms
-
Alternating Least Squares (ALS)
Initialize user and item latent factor vectors randomly
do
(1) Update every item latent factor vector by linear regression
(2) Update every user latent factor vector by linear regression
until Convergence - Guarantee in-sample error decreases during alternating minimization.
p_u = (Q^TQ+\lambda I)^{-1}Q^Tr_u
q_i = (P^TP+\lambda I)^{-1}P^Tr_i
E_{in}
(q_i)_{d \times 1} = ((P^T)_{d \times|U|}(P)_{|U| \times d}+\lambda I_{d \times d})^{-1}(P^T)_{d \times|U|}(r_i)_{|U| \times 1}
(p_u)_{d \times 1} = ((Q^T)_{d \times|I|}(Q)_{|I| \times d}+\lambda I_{d \times d})^{-1}(Q^T)_{d \times|I|}(r_u)_{|I| \times 1}
Learning Algorithms
- SGD has a better execution time than ALS.
- However, Parallelization can be applied to ALS.
- All user latent factor vectors computations are independent of other user latent factor vectors.
- All item latent factor vectors computations are independent of other item latent factor vectors.
Adding Bias
- Bias (Intercept):
User bias: Some users tend to give higher ratings than other user
Item bias: Some items tend to receive higher ratings than other item - Biases can be modeled by
Adding Bias
- New rating with biases:
- The observed rating is broken down into 4 components:
{ Global average, Item bias, User bias, User-item interaction } - This allows the 4 components to be explained independently.
- New Objective function:
Cold Start Problem
- Relieve cold start problem: Add external sources
- External sources: Implicit feedback (e.g. browsing history)
- Express the cold start user latent factor vector as:
where denotes the set of items for which user u expressed an implicit preference and
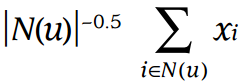
N(u)
Cold Start Problem
- External sources: Known user attributes (e.g. demographics)
- Express the cold start user latent factor vector as:
where denotes the set of user-associated attributes and
A(u)
Cold Start Problem
- The corresponding objective function becomes:
- Item cold start problem can be dealt with in a similar way.
- Note that usually lack of data problem happens more on user than on item.
Temporal Dynamics
- User taste and Item popularity may change temporally.
- Model several components as a function of time:
{ Item biases, User biases, User preferences } - Note that the item latent factor vectors are not expressed in a function of time since items are rather static comparing to humans.
Confidence Levels
- Sometimes not all observed ratings deserve the same weight or confidence.
e.g. Ratings tilted by adversarial users - The corresponding objective function becomes:
where denotes the confidence level
c_{ui}
# of dims in the latent factor vector
[IEEE-Computer][2009][Matrix Factorization Techniques For Recommender Systems]
By dreamrecord
