Improving Latent Factor Models via Personalized Feature Projection for One Class Recommendation
Tong Zhao, Julian McAuley, Irwin King
CIKM'15
Motivation (1/2)
- Latent factor models use inner product to represent a user's compatibility with an item.
- However, a user’s opinion of an item may be more complex.
- Each dimension of each user’s opinion may depend on a combination of multiple item factors simultaneously.
- It may be better to view each dimension of a user’s preference as a personalized projection of an item’s properties.
Motivation (2/2)
- A personalized feature projection (PFP) method is proposed to learn users’ latent features as a personalized projection matrix instead of a vector.
- A user's opinion of an item is no longer modeled by a real number but a vector.
- Vector-based objectives can be formulated, which provides more flexible structures to describe users’ preferences.
5
5
10
10
Methodology (1/10)
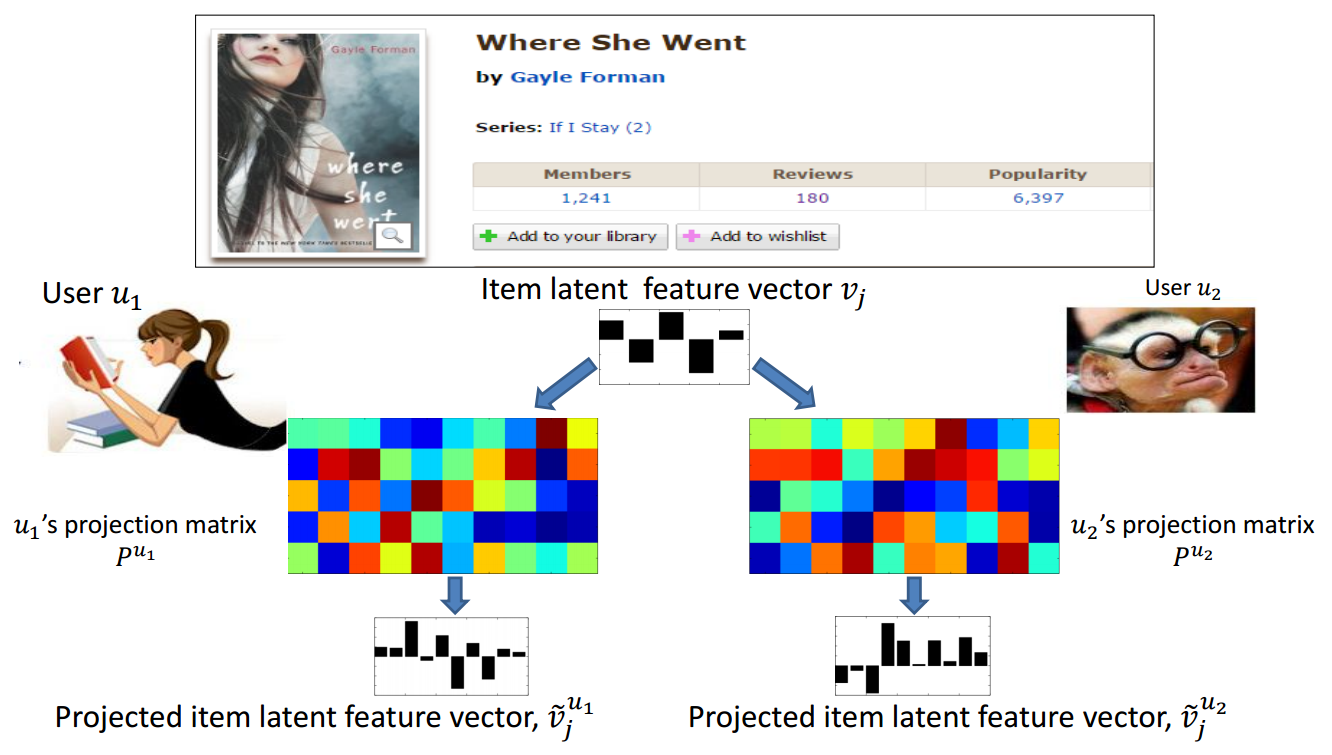
- Each user is modeled as a personalized projection matrix.
- For a specific user u, each item vector is projected by multiplying u’s personalized projection matrix.
- When K*=1, PFP reduces to the original latent factor model.
P^u=R^{K \times K^*}, P^u_f=R^K
\tilde{v_j}=v_jP^u
Methodology (2/10)
- Then u's preference toward item j is modeled by summarizing all the projected feature vectors from his / her positive feedback.
- Assumption: The projected feature vectors of users’ positive feedback items should be closer to users’ average taste than are the negative feedback items.
- The average similarity makes the approach insensitive to the choice of which positive feedback items should be selected.
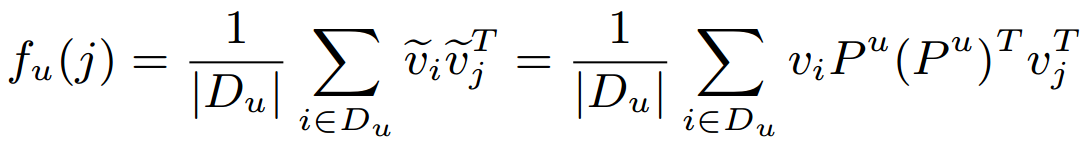
f_u(i) \succ f_u(j)
Methodology (3/10)
- Personalized Feature Projection (PFP) for one class recommendation.
- Three objective functions for optimizing ranking:
- Area under the ROC curve (AUC) Loss
- Weighted Approximated Ranking Pairwise (WARP) Loss
- Kullback–Leibler divergence (KL-divergence)
Methodology (4/10)
- Area under the ROC curve (AUC) Loss
- Apply Bayesian Personalized Ranking (BPR) framework.
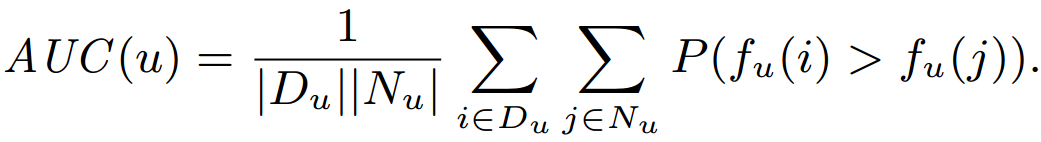
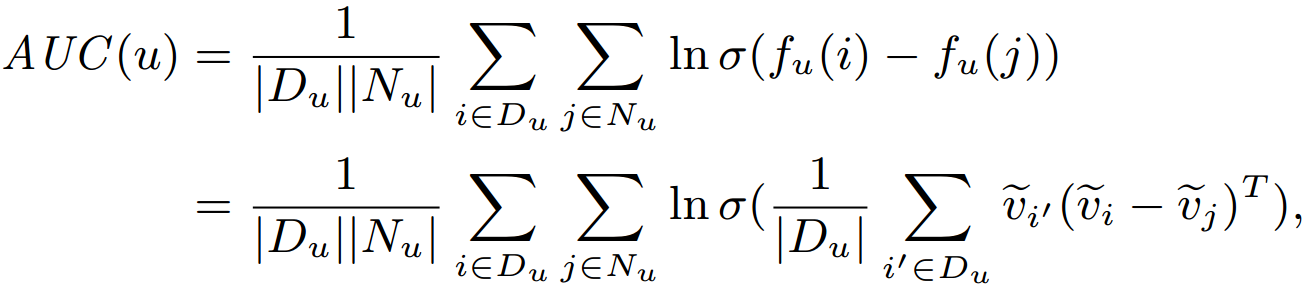
Methodology (5/10)
- Weighted Approximated Ranking Pairwise (WARP) Loss
- Θ is a function which transforms the predicted rank of item i into a loss value.
- Θ is a function which transforms the predicted rank of item i into a loss value.
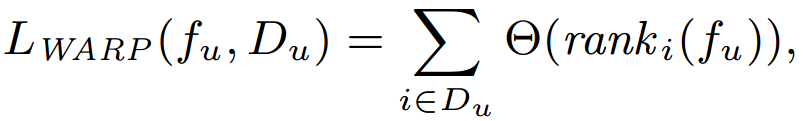
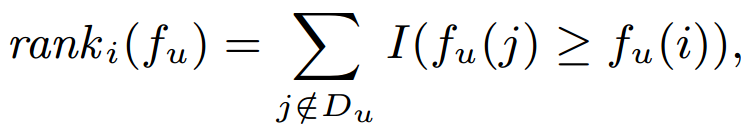
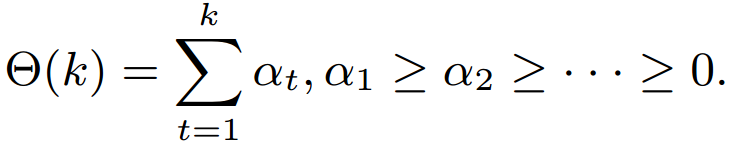
\alpha_t=\frac{1}{N}
\alpha_t>\alpha_{t+1}\ \ e.g.\ \frac{1}{t}
| Optimize mean rank | |
| Assign higher importance to the top-ranked item |
Methodology (6/10)
- Weighted Approximated Ranking Pairwise (WARP) Loss
- Since computing costs too much, we uniformly sample a negative feedback instance until a pairwise violation is found.
where Q is the steps required to find a pairwise violation
- Since computing costs too much, we uniformly sample a negative feedback instance until a pairwise violation is found.
'
'
'
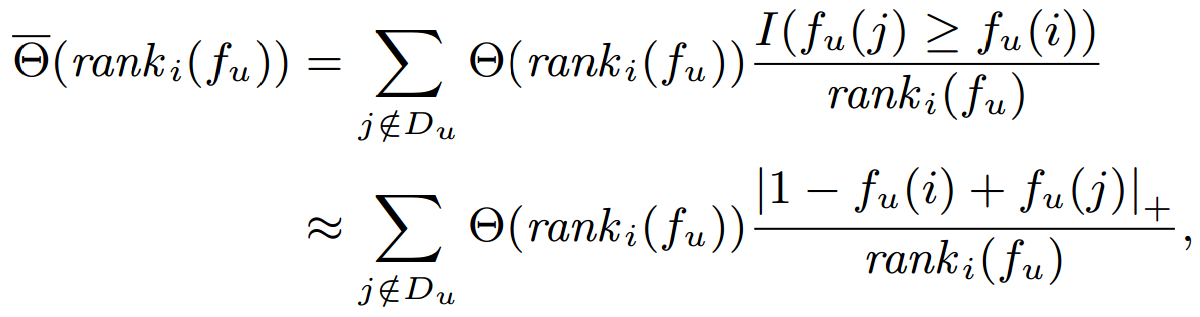
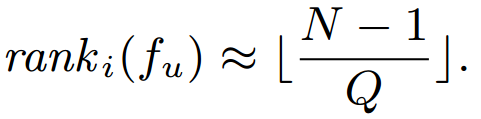
rank^{'}_i(f_u)
Methodology (7/10)
-
Weighted Approximated Ranking Pairwise (WARP) Loss
-
The loss of a chosen (u, i, j) triple becomes
- Apply gradient descent to perform updates.
-
The loss of a chosen (u, i, j) triple becomes
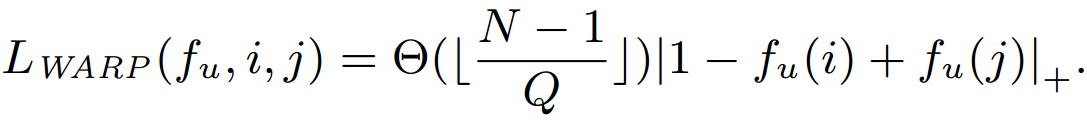
Methodology (8/10)
- Kullback–Leibler divergence (KL-divergence)
- PFP models a user's preference on an item via a projected vector.
- Thus users’ preference differences on items can be modeled in vector space.
- Maximize the KL-divergence between the projected vectors from users’ positive and negative instances.
- KL-divergence
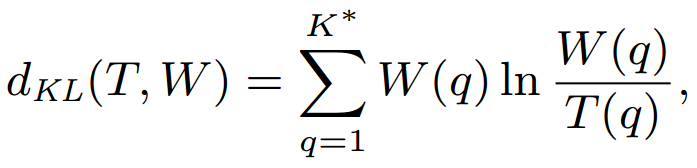
Methodology (9/10)
- Kullback–Leibler divergence (KL-divergence)
- Objective function for a pair of positive and negative item (i, j)
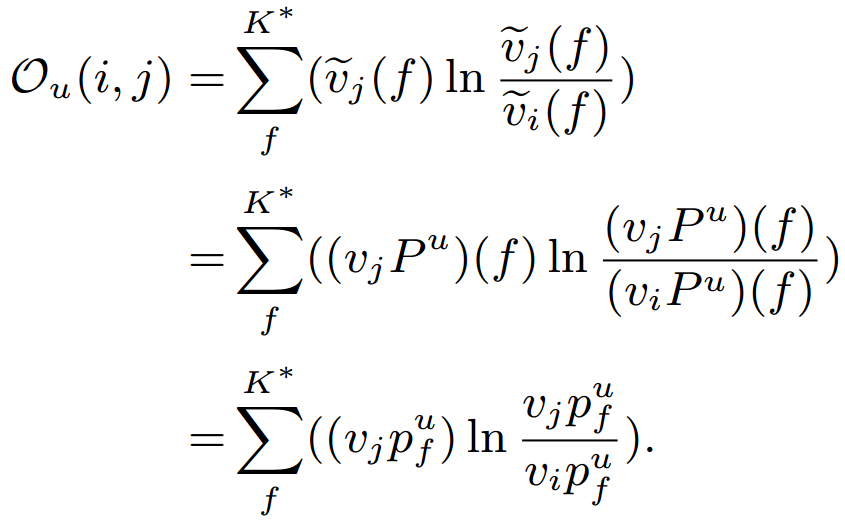
Methodology (10/10)
- Kullback–Leibler divergence (KL-divergence)
- Apply gradient ascent to perform updates.
- Some constraints to avoid overfitting.
- Apply gradient ascent to perform updates.
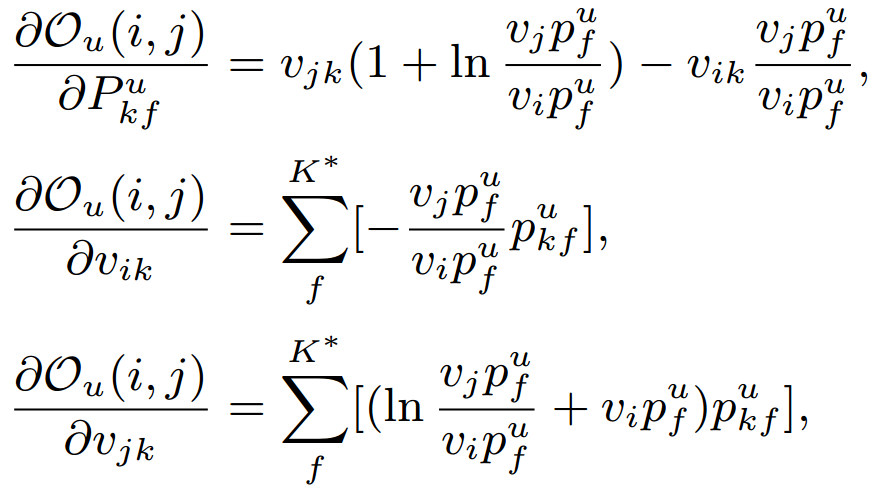
Experiments (1/5)
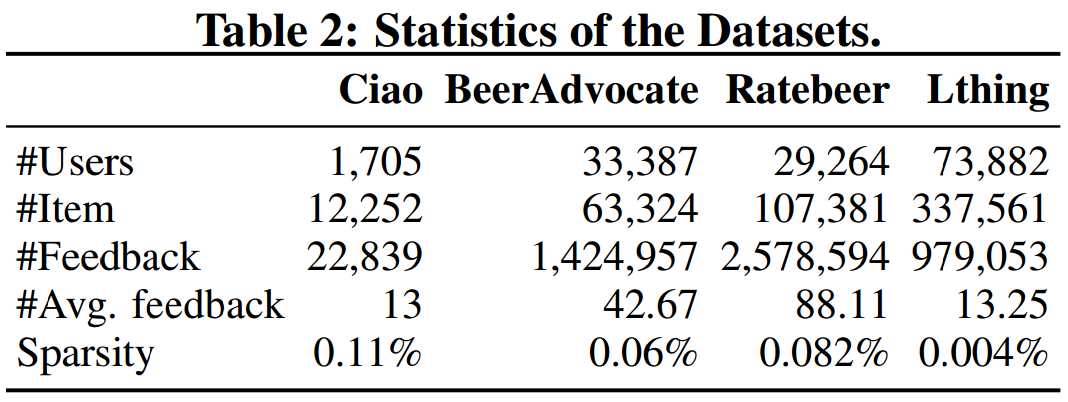
- Datasets
- Keep ratings >= 4 to make positive feedbacks.
- Randomly split 10% ratings to be testing.
- Evaluation metrics
- AUC
- NDCG
Experiments (2/5)
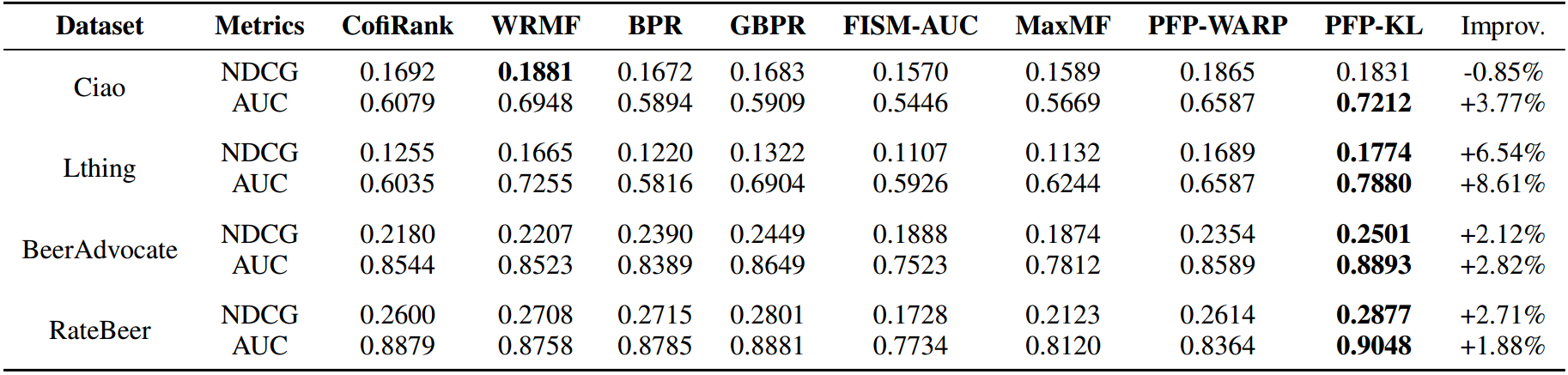
PFP-KL generally outperforms PFP-WARP
Experiments (3/5)
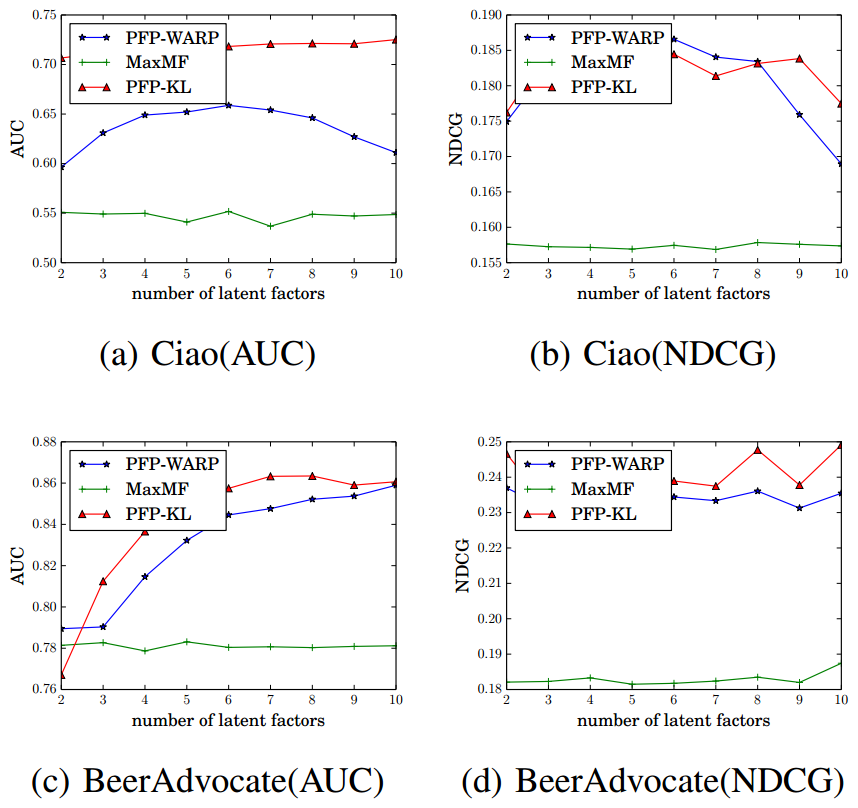
Embedding size is too small...
- Impact of #latent factors
Experiments (4/5)
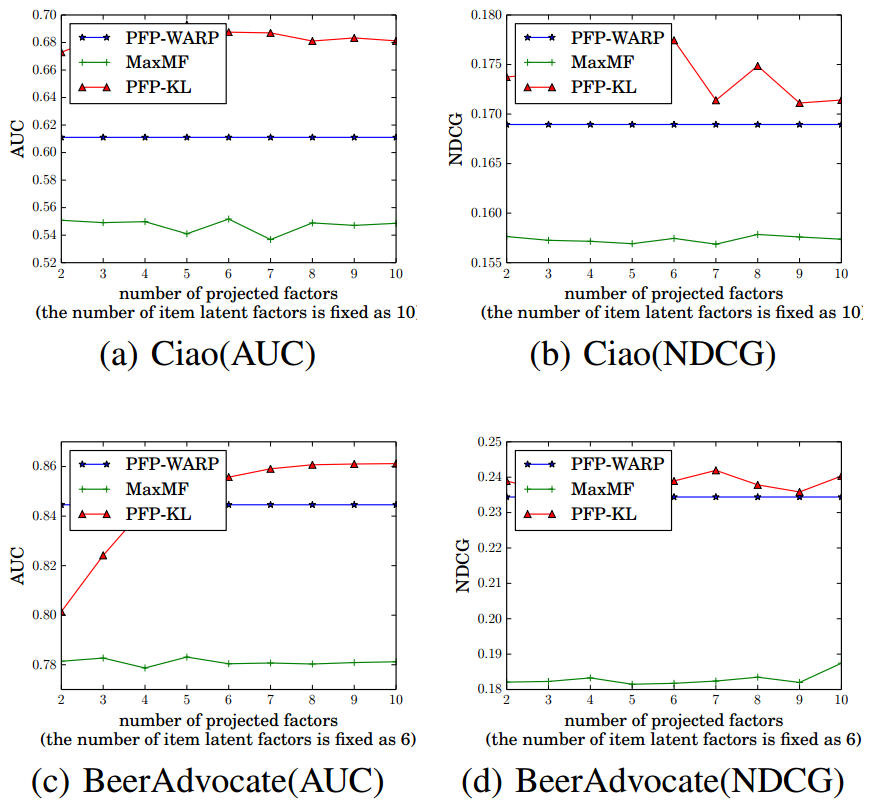
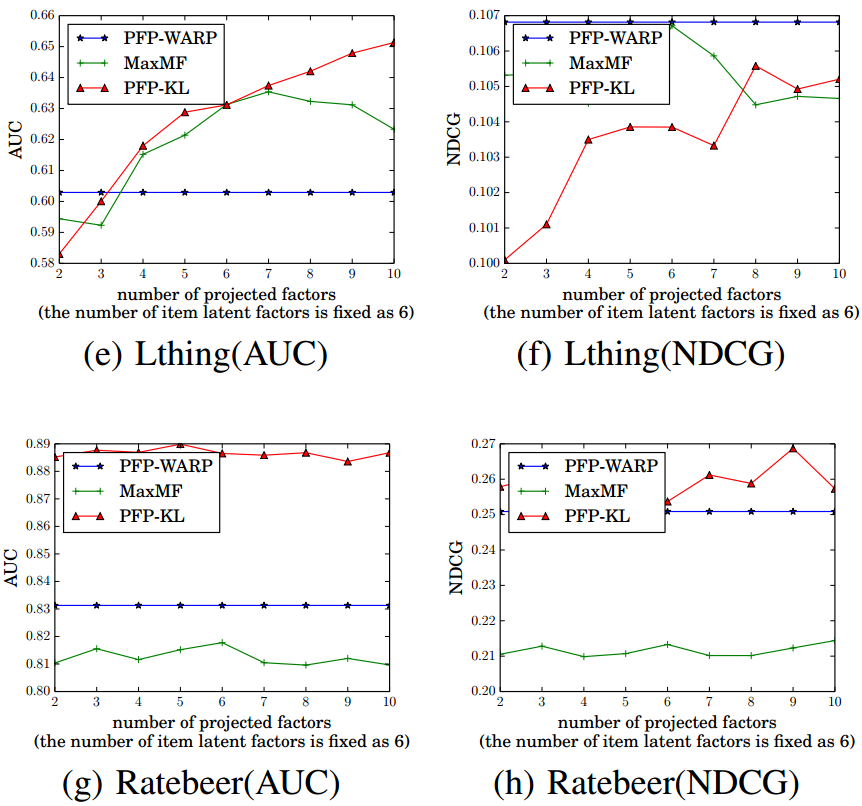
- Impact of #projected factors
Q: Why does PFP-WARP's performance is independent of #projected factors ?
Experiments (5/5)
- Observations
- When K* is small, PFP-KL cannot make use of such a low-dimensional projection space to describe users’ preferences.
- When observed feedback is sufficient for training, a large projection number can be applied to better model user tastes.
- When limited observed feedback is provided, the projection number should be decreased to avoid overfitting.
Conclusion
- The authors proposed Personalized Feature Projection (PFP) method to capture the complexities of users' preferences towards certain items over others.
- PFP assumes each dimension of a user’s preference is related to a combination of item factors simultaneously.
- It is unclear of the meaning behind each projected latent factor.
[CIKM][2015][Improving Latent Factor Models via Personalized Feature Projection for One Class Recommendation]
By dreamrecord
