Speeding Up the Xbox Recommender System Using a Euclidean Transformation for Inner-Product Spaces
Yoram Bachrach, Yehuda Finkelstein,
Ran Gilad-Bachrach, Liran Katzir,
Noam Koenigstein, Nir Nice, Ulrich Paquet
Microsoft Research
RecSys'14
Background
- Matrix Factorization:
- A dimensionality reduction technique
- Recommend items by sorting all user-item inner products. - Drawbacks:
When it comes to online recommender system which must adhere to strict response-time constraints,
- Require huge computation cost
- Slow
To deal with this problem...
- Map the maximum inner product search problem to Euclidean space nearest neighbor search problem.
- Do approximate matches on PCA-Tree with neighborhood boosting technique applied.
- A trade-off between a slight degradation in the recommendation quality and a significant improvement in the retrieval time.
Modern Recommender Systems
- 2 major parts:
(1) The learning phase
A model is learned (offline) based on user feedback.
(2) The retrieval phase
Recommendations are issued per user (online). - This paper focus on the scalability of the retrieval phase based on MF.
- Xbox recommendation system:
- A Bayesian MF model
- user, item latent factor vectors of #dim = 50
The Retrieval Problem
- Given a user represented by a vector , and all the item vectors , recommend the items with the higher inner products .
- Problems:
(1) #items is too large, HUGE computation cost for each users if linear scan is applied.
(2) Some contextual information is only available during user engagement, so the retrieval phase can not be done offline.
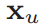

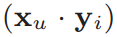
MF-based Recommeder System
- Baseline model
- and do not affect the ranking of items for a given user.
- With a new representation:
the problem becomes a search problem in an inner-product space
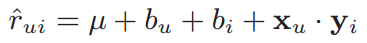
\mu
b_u
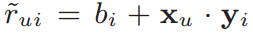
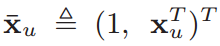
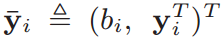
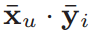
Previous Approach
- 2 basic approaches:
(1) Propose new recommendation algorithms in which the prediction rule is not based on inner-product matches.
- Khoshneshin et al. (RecSys '10)
Do nearest-neighbor search on Euclidean space.
- Noam Koenigstein and Yehuda Koren (RecSys '13)
An item-oriented model which embeds items in a Euclidean space.
* Problem:
It deviates from the well familiar MF framework.
Previous Approach
- 2 basic approaches:
(2) Design new algorithms to mitigate maximal inner-product search.
- Noam Koenigstein, Parikshit Ram, and Yuval Shavitt (CIKM '12)
A new IP-Tree data structure + branch-and-bound search + spherical user clustering that allows to pre-compute and cache recommendations to similar users.
* Problem:
Requires prior knowledge of all the user vectors.
(Not applicable to RecSys with ad-hoc contextual info is used.)
Our Approach
- A novel transformation that reduces the maximal inner-product problem to simple nearest neighbor search in a Euclidean space.
- It can be employed by any classical MF model.
- It enables using any of the existing algorithms for Euclidean spaces.
Nearest Neighbor in Euclidean Spaces
- Locality Sensitive Hashing (LSH)
- KD-trees
- Principal component axes trees (PCA-Trees)
- Principal Axis Trees (PAC-Trees)
- Random Projection Trees (RPT)
- Maximum Margin Trees (MMT)
Definition of a search problem
- Function retrieves the index of an item in for a given query .
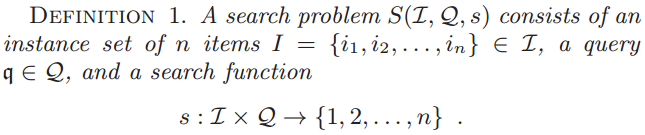
s
I
q
Reducible Search Problem
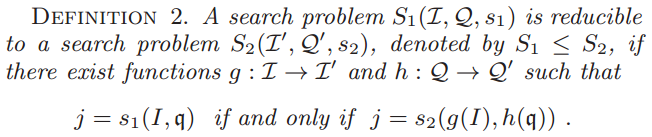
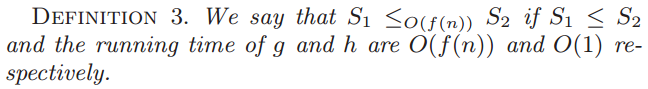
pre-processing
query time
3 Reducible Problems
- Maximum inner product (MIP)
- Nearest neighbor (NN)
- Maximum cosine similarity (MCS)
MCS_{n,d} \leq_{O(n)} MIP_{n,d} \leq_{O(n)} NN_{n,d+1}
\leq_{O(n)}
MCS_{n,d+1} ...
Only this one is used in this paper.
3 Reducible Problems
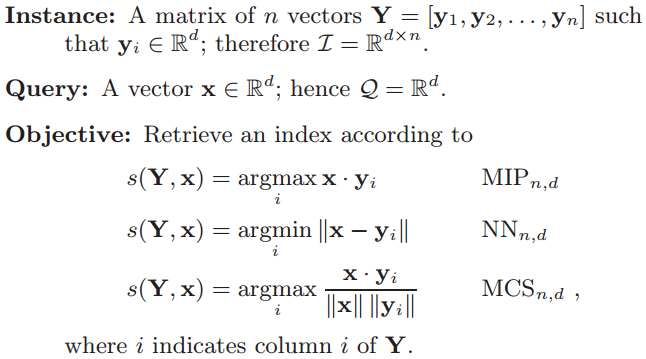

\|\tilde{y}_i\|^2

(-1,2x^T)^T
-\|y_i\|^2+2x \cdot y_i
.\ Finally,

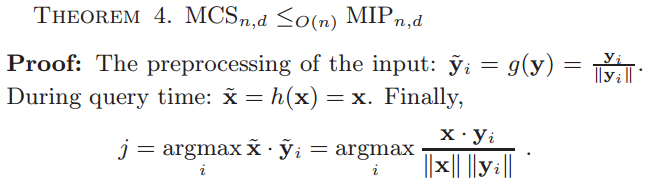

NN_{n,d+1}
Why consider reducibility?
- Many efficient search data structures rely on the triangle inequality.
- The triangle inequality does not hold on inner product space!
i.e. The following does not hold.
x \cdot y_i + x \cdot y_j > y_i \cdot y_j
y_i \cdot y_j + x \cdot y_j > x \cdot y_i
x \cdot y_i + y_i \cdot y_j > x \cdot y_j
Reduction
- Reduce MIP search problem to NN search by Theorem1.
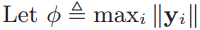
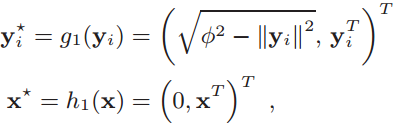
Reduction
- NN is invariant to shifts and rotations in the input space.
- We can compose the transformations with PCA rotation and still keep an equivalent search problem.
-
, and be a matrix with µ replicated along its columns, then the SVD of the centered data matrix is
-
(1) An matrix with orthonormal eigenvectors
(2) Each defines a hyperplane onto which each
is projected.
(3) Matrix W is a rotation matrix that aligns the vectors to their principal components.
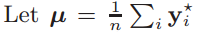
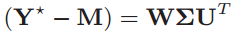
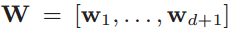
w_j
y_j^*-\mu
Reduction
- Do PCA rotation on the these latent factor vectors:
- Composition of the two transformations:
- After this transformation, the points are rotated so that their components are in decreasing order of variance (importance).
- Thus an Euclidian search can be performed.
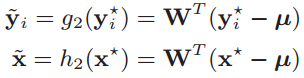
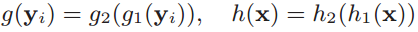

Index vectors with PCA-Tree
- The axes are aligned with the principal components of .
-
PCA-Tree:
Do KD-Tree on PCA-axis. - The top principal components are used.
- Each item vector is assigned to its representative leaf.
d+1
Y^*
d' \leq d + 1

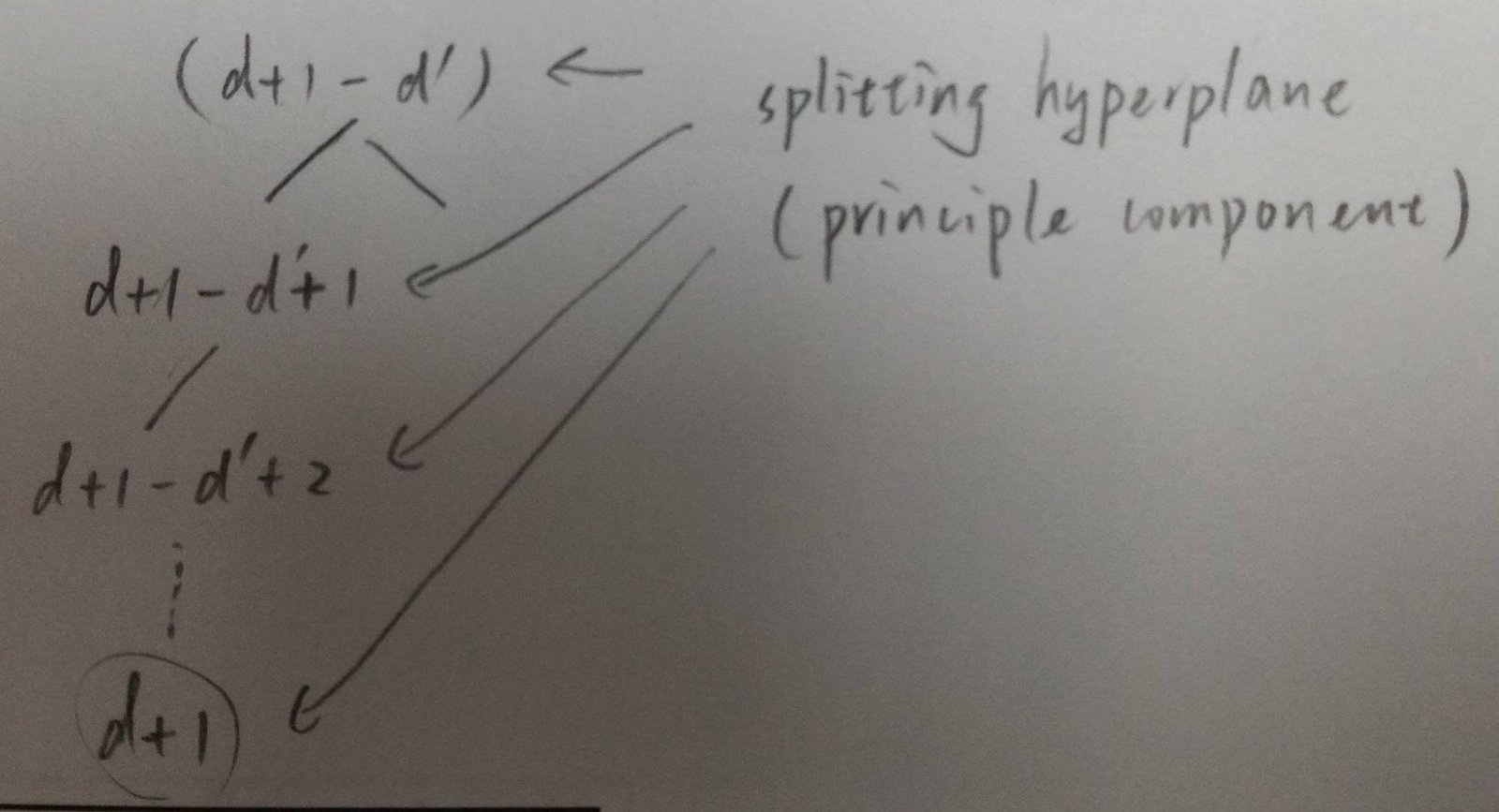
Fast Retrieve with PCA-Tree
- Transform user vector and traverse the tree to the appropriate leaf.
- #items in each leaf decays exponentially in the depth of the tree.
-
Trade-off between speedup and accuracy:
With a larger d, a smaller proportion of candidates are examined, resulting in a larger speedup, but also a reduced accuracy.
\tilde{x}=h(x)
d'
Neighborhood Boosting
- It is possible that some of the optimal top K vectors are indexed in other leafs and most likely the adjacent leafs.
- Also consider the item vectors on the leaves with a Hamming distance of 1.
- Thus more leaves are considered for one query.
- Instrumental in achieving the best balance between speedup and accuracy.
d'-1
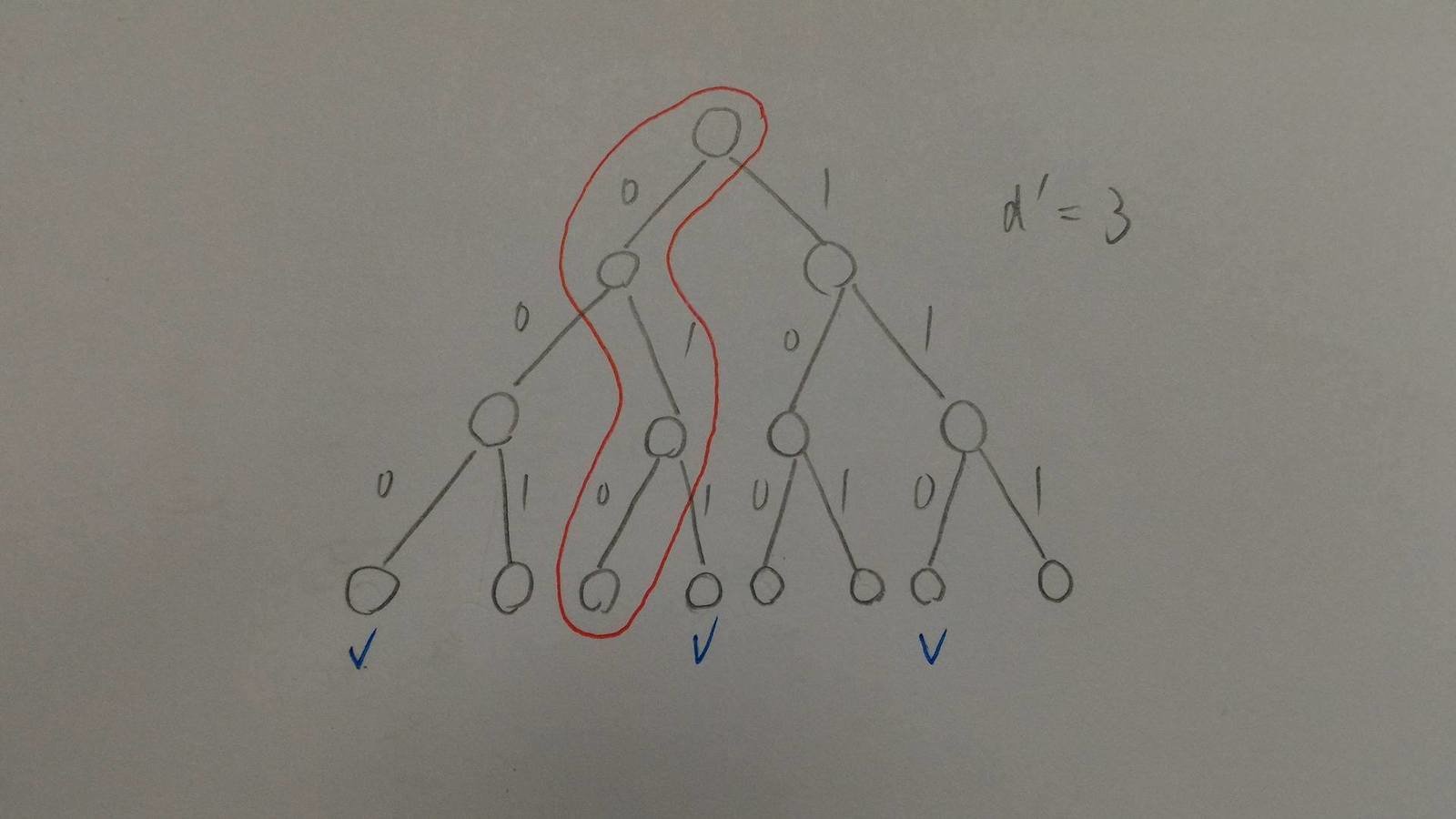
Evaluation Dataset
- Xbox Movies:
- 100 million binary ratings
- 5.8 million users
- 15K movies - Yahoo! Music:
- 252.8 million ratings of scale 0-100
- 1 million users
- 624.9K musics - Extract user and item latent factor vector of #dim = 50 from both of them.
Evaluation Metrics
- Speedup values:
is the linear scan algorithm. - Only online processing time is considered.
- The higher the better.
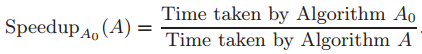
A_0
Evaluation Metrics
- Precision@K:
- RMSE@K:
It is possible to have low Precision rates but still recommend very relevant items (with a high inner product between the user and item vectors).
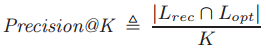
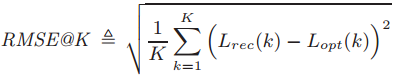

Current State-of-the-art
-
Noam Koenigstein, Parikshit Ram, and Yuval Shavitt (CIKM '12)
* 2 phases
(1) IP-Tree + user cones
Assume all the user vectors are computed in advance and can be clustered into a structure of user cones.
(2) Branch-and-bound search in metric-trees
A space partitioning tree which partitions vectors according to Euclidean proximity.
Current State-of-the-art
-
Noam Koenigstein, Parikshit Ram, and Yuval Shavitt (CIKM '12)
* Problem:
(1) Requires prior knowledge of all the user vectors.
Not applicable for recommender systems like Xbox whose user vectors are computed or updated online.
(2) Partitions vectors on Euclidean space, not inner-product space.
Can be solved by applying the transformation of Theorem 1.
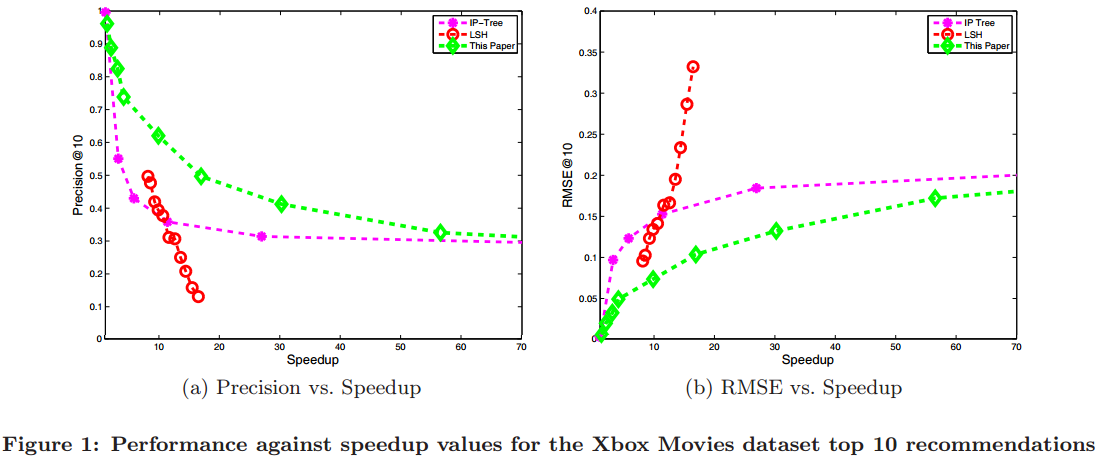
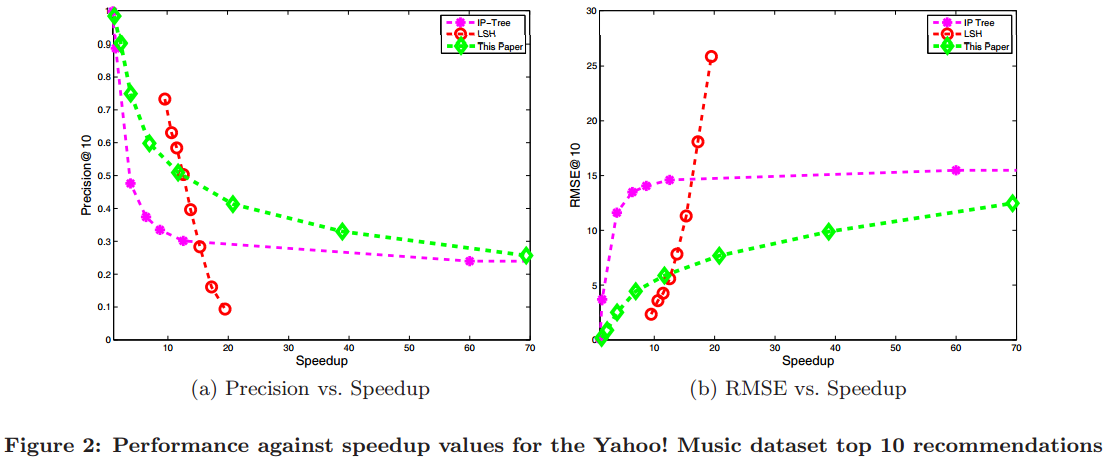
RMSE values are larger because Yahoo! Music's ratings have a scale of 0-100.
Obervations
- LSH's performance drops significantly when higher speedup values are considered.
Reason: Our transformation add one relatively large dimension to the vector which results in a difficult distribution for LSH. -
RMSE values remain low even if precision values are low.
- It indicates that the recommended items are still very relevant to the user even if the list of recommended items is quite different from the optimal list of items.
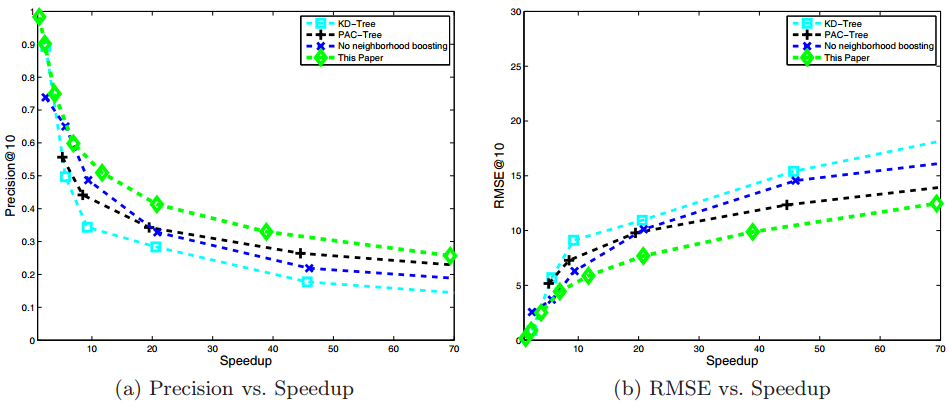
Conclusions
- Speed-up the retrieval process in a MF-based recommender system by:
(1) Map a maximal inner product search to Euclidean nearest neighbor search.
(2) Solve the Euclidean nearest neighbor problem using PCA-Trees. - It achieves superior quality-speedup trade-offs compared with state-of-the-art methods.
[RecSys][2014][Speeding Up the Xbox Recommender System Using a Euclidean Transformation for Inner-Product Spaces]
By dreamrecord
[RecSys][2014][Speeding Up the Xbox Recommender System Using a Euclidean Transformation for Inner-Product Spaces]
- 306



