Top-N Recommendation for Shared Accounts

Koen Verstrepen, Bart Goethals

University of Antwerp, Belgium

RecSys'15

Background

• Multiple users often share a single account.
• Often no contextual information is available to distinguish different users in a single account.
• It yields 3 problems.
• Currently no prior research on this topic.

Prob1: Dominance Problem

• All recommendations are relevant to only some of the users that share the account and at least one user does not get any relevant recommendation.
•  We say that these few users dominate the account.

Prob2: Generality Problem

• The recommendations are only a little bit relevant to all users in the shared account, but are not really appealing to any of them.

Prob3: Presentation Problem

• Since all users share a single account, how does every user know which recommendation is meant for her?

Problem Definition

               : The set of users that share acct a.
               : The acct that user u belongs to. (exactly 1)
                      : user-rating-matrix

           : RecSys on T, item i is called relevant to user u if i is in the top-N recommendations for u 

Problem Definition

• Unfortunately, T is unknown.
• We are only given:                                                                                 : acct-rating-matrix
             : RecSys for shared acct on R, which computes top       recommendations for account a

Problem Definition

• Goal:                                                                           
  (1) Maximize top                     for every user in the acct a
             Dominance problem + Generality problem
  (2) Make it clear for a user in the user set of a which items in the top       are meant for him or her.
             Presentation problem

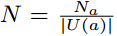
The Reference RecSys

• An Item-based CF by Deshpande et al.
•                                                                                            
  
  
  where

The Reference RecSys

• Choice for                 : cosine similarity
• Normalized cosine similarity by Deshpande et al.
•                                                                                            
   

Problem Illustration

few large contributions

many small contributions

Problem Illustration

• Yields Generality Problem:
  It does not discriminate between a recommendation score that is the sum of a few large contributions and a recommendation score that is the sum of many small contributions.

Problem Illustration

2:3

Problem Illustration

• Yields Dominance Problem:
  It does not take into account that        has more known preferences than       .
• Both of the 2 examples yields Presentation problem.

Solve Generality Problem

• length adjusted item-based recommendation score:
•                                                                                            
   
• By choosing p > 0, we create a bias in favor of the sum of a few large similarities. (p↑ => bias↑)
• Similar to the concept of normalization.

Solve Generality Problem

• Formally, we want to rank all items i according to:            
   
• Since we only have I(a), we approximate it with an upper bound:
   
• This is because every set of items I(u) for which u∈U(a) is also an element of the power set of I(a), which is        .
• The subset of I(a) which corresponds to users are more likely to result into the highest recommendation scores than the subset consists of random items.

Solve Generality Problem

• The disambiguating item-based (DAMIB) recommender system:
  
  
   
• When                    is high, we expect that      corresponds well to an individual user.
• When                    is low, there is no user in the shared account for whom i is a strong recommendation and we expect       to be a random subset.

Efficient Computation

•      can be computed in                  time instead of exponential time since:                                                                         

Efficient Computation

• Proof:                                                                         

Solve Dominance Problem

• Use the DAMIB scores to find the       highest scoring candidate recommendations.
• Avoid recommending the items whose explanation         is not sufficiently different from the explanations of the higher ranked recommendations.
• The difference measuring metric:

All highly relevant recommendations to individual users have already been recommended => Clean the set C(a)

Still need to recommend the items which fail to meet the red conditions since Na recommendations are required.

Solve Presentation Problem

• Present every recommendation                             together with its explanation      .
• e.g.
  Recommend item r with its similar items s1, s2 and s3. A user will recognize s1, s2 and s3 as her preferences, and know that r is recommended to her.

Experiments

• Source code available on https://bitbucket.org/BlindReview/rsa (No permission)
• Datasets with shared account info are rarely seen.
• However, we can create synthetic shared accounts by randomly grouping users in groups of 2, 3 or 4.               
• Datasets:
  (1) Yahoo!Music
  (2) Movielens1M
  (3) Book-Crossing
  (4) Wiki10+

Performance Evaluation

• Performance evaluation metrics:
  (1) Recall of user u:
  
  
  (2) The fraction of users that does not get any relevant recs:
   

where

Performance Evaluation

• Competitors:
  (1) IB: The original item-based Rec Sys (Baseline)
  (2) IB-COVER: COVER(a,IB)
  (3) DAMIB-COVER with p = 0.5
  (4) DAMIB-COVER with p = 0.75

Q: DAMIB-COVER has a bad performance when accounts are not shared?

• The author claims that DAMIB-COVER algorithm still performs well when no accounts are shared.
• By Deshpande et al.
  Randomly choose 1 preference of every user to be the test preference       for that user.
• Performance evaluation metric: Hit rate at 5

Performance Evaluation

POP: The baseline-algorithm which is a non-personalized algorithm that ranks all items according to their popularity, i.e. the number of users in the training set that prefer the item.

• Performance evaluation metric for presentation problem:
  
   
• The DAMIB-COVER explanations are superior to the
  IB-COVER explanations.

Performance Evaluation

Related Work

• [TKDE'08][Using context to improve predictive modeling of customers in personalization applications][C. Palmisano, A. Tuzhilin, and M. Gorgolione]
• [WebMine'06][Contextual recommendation][S. Anand and B. Mobasher]
• [UAI'12][Guess who rated this movie: Identifying users through subspace clustering][A. Zhang, N. Fawaz, S. Ioannidis, and A. Montanari]
  (Synthetic Account Evaluation Approach)
• [ICDE'09][Recommendation diversification using explanations][C. Yu, L. Lakshmanan, and S. Amer-Yahia]
  (Diversity Enhancement, Solution similar to IB-COVER)

Conclusions and Future Work

• The widely used item-based Rec Sys fails when it makes recommendations for shared accounts.
• The DAMIB-COVER algorithm overcome the challenge of recommendation for shared accounts in the absence of contextual information. 
• The computation of a recommendation score cost 
                 instead of exponential time.
• Planning to generalize the proposed solution to a wider range of Rec Sys.