jax-cosmo: Finally an Automatically Differentiable Cosmology Library!

2021 July DESC Collaboration Meeting

Francois Lanusse (@EiffL), for the jax-cosmo contributors

And more (not yet in the picture because I'm lagging behind on PR merging)

- Jean-Eric Campagne

- Joe Zuntz

- Tilman Troester

- Ben Horowitz

Why
do you want
any of this?

Fisher Forecasts become exact and instantaneous

import jax
import jax.numpy as np
import jax_cosmo as jc

# .... define probes, and load a data vector

def gaussian_likelihood( theta ):
  # Build the cosmology for given parameters
  cosmo = jc.Planck15(Omega_c=theta[0], sigma8=theta[1])

  # Compute mean and covariance
  mu, cov = jc.angular_cl.gaussian_cl_covariance_and_mean(cosmo,
                                                    ell, probes)
  # returns likelihood of data under model
  return jc.likelihood.gaussian_likelihood(data, mu, cov)

# Fisher matrix in just one line:
F = - jax.hessian(gaussian_likelihood)(theta)

No derivatives were harmed by finite differences in the computation of this Fisher!
You can scale to thousands of input parameters, no issues of numerical precision.

Inference becomes fast and scalable

Gradients of the log posterior are required for modern efficient and scalable inference techniques:
- Variational Inference
- Hamiltonian Monte-Carlo
With gradients, you can scale to thousands of parameters

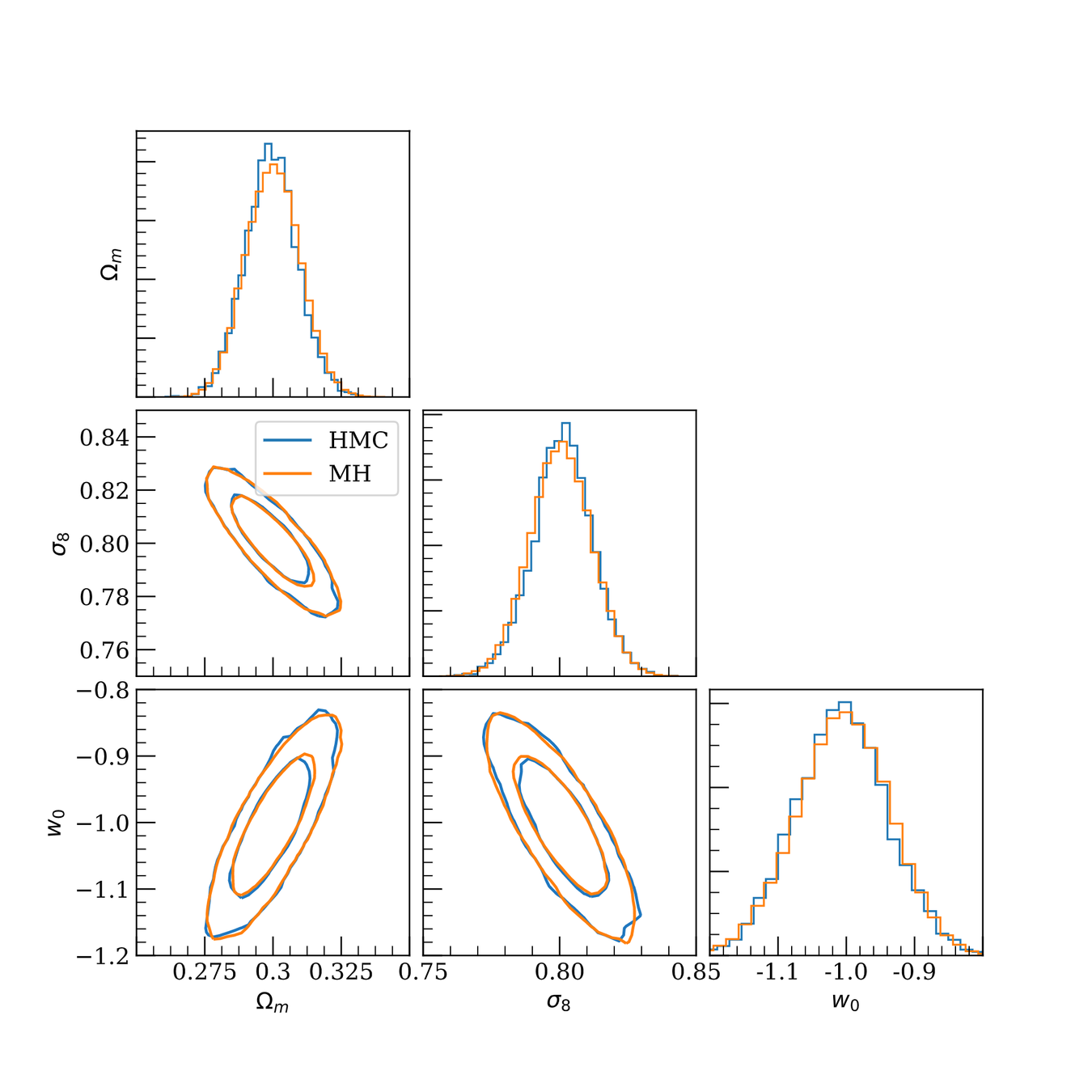
DES Y1 posterior, jax-cosmo HMC vs Cobaya MH
(credit: Joe Zuntz)

def log_posterior( theta ):
    return gaussian_likelihood( theta ) + log_prior(theta)

score = jax.grad(log_posterior)(theta)

You can differentiate through Cosmology

LSST DESC 3x2pt Tomography Challenge

Given (g)riz photometry, find a tomographic bin assignment method that optimizes a 3x2pt analysis.

Strategy with differentiable physics:
- Introduce a parametric "bin assignment function"
- Optimize this function to maximize DETF FoM

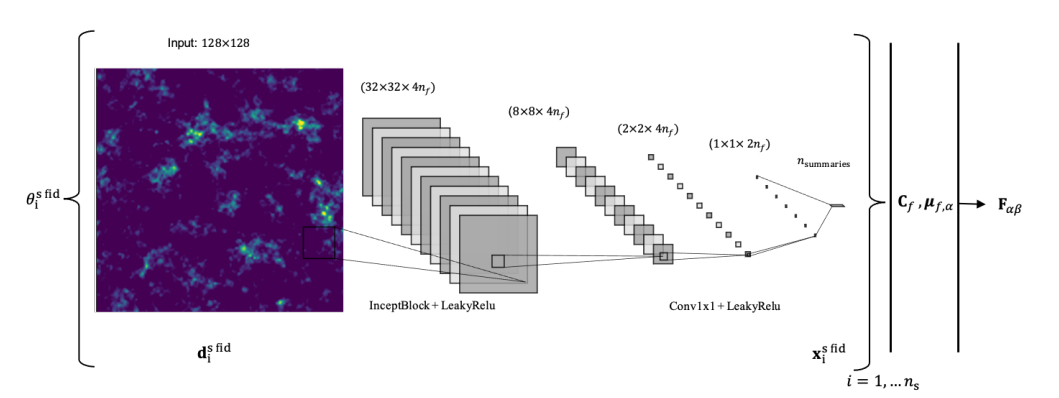
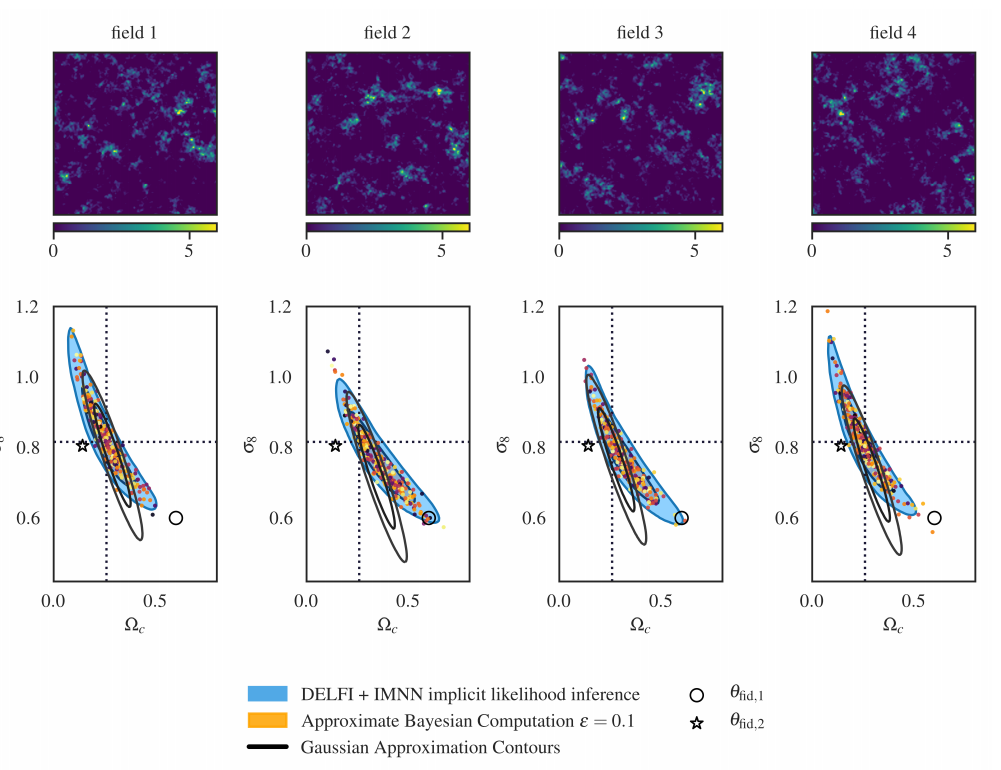
Differentiable Physics for Score Compression

Makinen et al. 2021, arXiv:2107.07405

What Framework Should you Adopt?

Some top-level considerations

[Low Barrier to Entry] You don't want contributors to have to learn an entirely new language to start contributing (I'm looking at you Julia!).
[Maintainability] You want readable code, without several layers of implementation (I'm looking at you GalSim and CCL!)
[Trivially installable] This should always work:
[Performance] Duh! But more precisely, you want to be able to take advantage of next gen platforms like Perlmutter. Code should work 100% the same on CPU or GPU for the user.

$ pip install mylibrary

=> a JAX-based library will meet all of these criteria

What
Is
JAX?

Credit

JAX: NumPy + Autograd + XLA

JAX uses the NumPy API
=> You can copy/paste existing code, works pretty much out of the box
JAX is a successor of autograd
=> You can transform any function to get forward or backward automatic derivatives (grad, jacobians, hessians, etc)
JAX uses XLA as a backend
=> Same framework as used by TensorFlow (supports CPU, GPU, TPU execution)

import jax.numpy as np

m = np.eye(10) # Some matrix

def my_func(x):
  return m.dot(x).sum() 

x = np.linspace(0,1,10)
y = my_func(x)

from jax import grad

df_dx = grad(my_func)
 
y = df_dx(x)

Pure functions
=> JAX is designed for functional programming: your code should be built around pure functions (no side effects)
- Enables caching functions as XLA expressions
- Enables JAX's extremely powerful concept of composable function transformations
Just in Time (jit) Compilation
=> jax.jit() transformation will compile an entire function as XLA, which then runs in one go on GPU.
Arbitrary order forward and backward autodiff
=> jax.grad() transformation will apply the d/dx operator to a function f
Auto-vectorization
=> jax.vmap() transformation will add a batch dimension to the input/output of any function

def pure_fun(x):
  return 2 * x**2 + 3 * x + 2


def impure_fun_side_effect(x):
  print('I am a side effect')
  return 2 * x**2 + 3 * x + 2


C = 10. # A global variable
def impure_fun_uses_globals(x):
  return 2 * x**2 + 3 * x + C

# Decorator for jitting
@jax.jit
def my_fun(W, x):
  return W.dot(x)

# or as an explicit transformation
my_fun_jitted = jax.jit(my_fun)

def f(x):
  return 2 * x**2 + 3 *x + 2

df_dx = jax.grad(f)   
jac = jax.jacobian(f)
hess = jax.hessian(f)

# As decorator
@jax.vmap
def f(x):
  return 2 * x**2 + 3 *x + 2

# Can be composed
df_dx = jax.jit(jax.vmap(jax.grad(f)))

jax-cosmo

Cosmology library embracing JAX computing model
=> Autodiff, GPU acceleration, automated batching
MIT licensed, collaboratively developed
=> Follows the all-contributors guidelines
Inspired by CCL's tracer mechanism
=> See design document
Unit tested against CCL

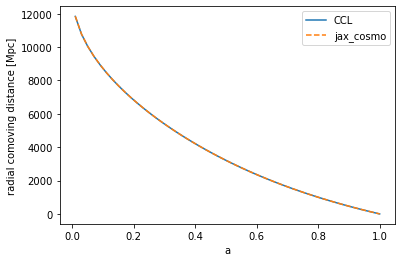
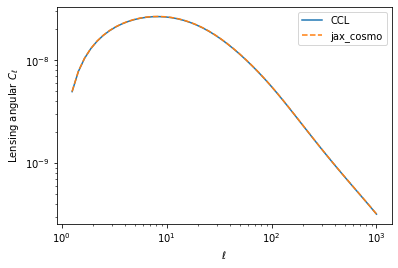
Status of Implementation

Certainly not feature-complete but approximately DES Y1 3x2pt capable
- Power spectrum:
  - Eisenstein-Hu Power
  - halofit
- Tracers:
  - Lensing (including NLA, multiplicative bias)
  - NumberCounts
- 2pt functions
  - Limber, harmonic space
  - Gaussian covariance tools
These were the main features needed for the DESC 3x2pt Tomo Challenge
- Took about a week to implement, another week to tidy up a bit

Let's take it for a spin

My
Two
Cents

JAX vs Julia vs TensorFlow vs PyTorch

Let's go with JAX:
- It's normal NumPy, don't need to learn anything new
- Under the hood, they will all use XLA, so no difference
- Very powerful function transformation mechanisms

Do We Need to Rewrite CCL from Scratch?

Yes, if we want differentiability there is no workaround.
Trying to progressively adapt CCL with differentiable components would be a nightmare.
But:
- When you already have a validated numerical scheme and implementation to compare to, there is no "research/uncertainty", it's purely a matter of translating code. I coded jax-cosmo in about a week.
  => CCL would continue to play a major role as a standard reference.
- It can be an opportunity to bring all of our experience in the design of a new library.

What about CAMB and CLASS?

Quick and Easy solution: train an emulator
- E.g. CosmoPower from A. Spurio Mancini
Longer term solution:
- Someone (maybe Zack) will code a differentiable version of those
- We could kickstart such a project

Where to host such projects?

These tools will be useful to all modern cosmological surveys, but they are non trivial to implement, test, and maintain.
- You want to ensure broad user adoption
- Help build a community to support the maintenance and development of the project
2 options:
- A DESC-sponsored project (like CCL), but developed completely openly (think astropy)
- Open project hosted in some sort of external entity, enabling anyone to contribute, across any collaboration.
  - That was the idea behind the Differentiable Universe Initiative
With our new DESC Software policy, I think option 1 is now doable.

In Conclusion...

But more seriously, happy to chat anytime if you are interested in contributing, or just want to know more about JAX :-)

jax-cosmo: Finally an Automatically Differentiable Cosmology Library!

Why do you want any of this?

Fisher Forecasts become exact and instantaneous

Inference becomes fast and scalable

You can differentiate through Cosmology

What Framework Should you Adopt?

Some top-level considerations

What Is JAX?

JAX: NumPy + Autograd + XLA

jax-cosmo

Status of Implementation

Let's take it for a spin

My Two Cents

JAX vs Julia vs TensorFlow vs PyTorch

Do We Need to Rewrite CCL from Scratch?

What about CAMB and CLASS?

Where to host such projects?

In Conclusion...

jax-cosmo

More from eiffl

Why
do you want
any of this?

What
Is
JAX?

My
Two
Cents