Probabilistic Learning

in JAX/Flax and TensorFlow Probability

 

Francois Lanusse @EiffL

+ p(x) =

Slides at: https://slides.com/eiffl/probabilistic-learning-jax

Our case study

Dynamical Mass Measurement for Galaxy Clusters

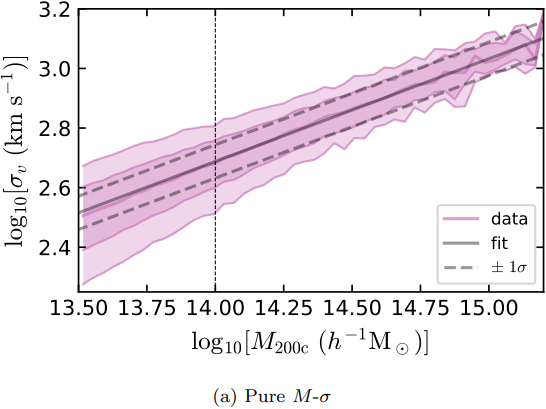
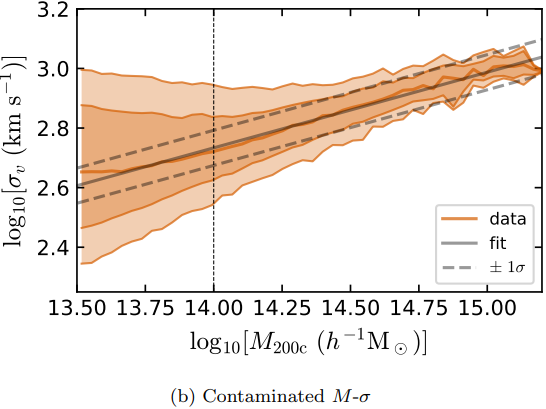
Figures and data from Ho et al. 2019

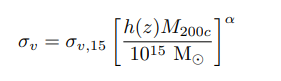
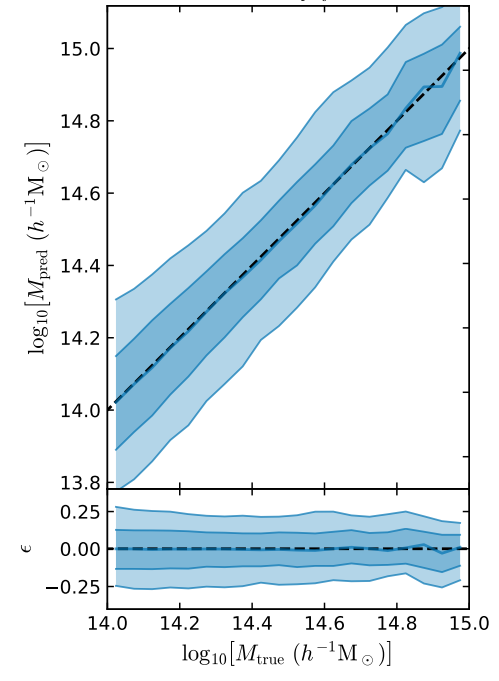
Our Goal: Train a Neural Network to Estimate Cluster Masses

What we will feed the model:

  • Richness
  • Velocity Dispersion
  • Information about member galaxies:
    • radial distribution
    • stellar mass distribution
    • LOS velocity distribution

Training data from MultiDark Planck 2 N-body simulation (Klypin et al. 2016) with 261287 clusters.

Why JAX? 

and what is it?

Credit

JAX: NumPy + Autograd + XLA

  • JAX uses the NumPy API
    => You can copy/paste existing code, works pretty much out of the box

     
  • JAX is a successor of autograd
    => You can transform any function to get forward or backward automatic derivatives (grad, jacobians, hessians, etc)

     
  • JAX uses XLA as a backend
    => Same framework as used by TensorFlow (supports CPU, GPU, TPU execution)
import jax.numpy as np

m = np.eye(10) # Some matrix

def my_func(x):
  return m.dot(x).sum() 

x = np.linspace(0,1,10)
y = my_func(x)
from jax import grad

df_dx = grad(my_func)
 
y = df_dx(x)
  • Pure functions
    => JAX is designed for functional programming: your code should be built around pure functions (no side effects)
    • Enables caching functions as XLA expressions
    • Enables JAX's extremely powerful concept of composable function transformations
       
  • Just in Time (jit) Compilation
    => jax.jit() transformation will compile an entire function as XLA, which then runs in one go on GPU.
     
  • Arbitrary order forward and backward autodiff 
    => jax.grad() transformation will apply the d/dx operator to a function f
     
  • Auto-vectorization
    => jax.vmap() transformation will add a batch dimension to the input/output of any function
def pure_fun(x):
  return 2 * x**2 + 3 * x + 2


def impure_fun_side_effect(x):
  print('I am a side effect')
  return 2 * x**2 + 3 * x + 2


C = 10. # A global variable
def impure_fun_uses_globals(x):
  return 2 * x**2 + 3 * x + C
# Decorator for jitting
@jax.jit
def my_fun(W, x):
  return W.dot(x)

# or as an explicit transformation
my_fun_jitted = jax.jit(my_fun)
def f(x):
  return 2 * x**2 + 3 *x + 2

df_dx = jax.grad(f)   
jac = jax.jacobian(f)
hess = jax.hessian(f) 

# As decorator
@jax.vmap
def f(x):
  return 2 * x**2 + 3 *x + 2

# Can be composed
df_dx = jax.jit(jax.vmap(jax.grad(f)))

Writing a Neural Network in JAX/Flax

import flax.linen as nn
import optax

class MLP(nn.Module):
  @nn.compact
  def __call__(self, x):
    x = nn.relu(nn.Dense(128)(x))
    x = nn.relu(nn.Dense(128)(x))
    x = nn.Dense(1)(x)
    return x
# Instantiate the Neural Network  
model = MLP()
# Initialize the parameters
params = model.init(jax.random.PRNGKey(0), x)
prediction = model.apply(params, x)
# Instantiate Optimizer
tx = optax.adam(learning_rate=0.001)
opt_state = tx.init(params)
# Define loss function
def loss_fn(params, x, y):
  mse = model.apply(params, x) -y)**2
  return jnp.mean(mse)
# Compute gradients
grads = jax.grad(loss_fn)(params, x, y)
# Update parameters
updates, opt_state = tx.update(grads, opt_state)
params = optax.apply_updates(params, updates)
  • Model Definition: Subclass the flax.linen.Module base class. Only need to define the __call__() method.

 

  • Using the Model: the model instance provides 2 important methods:
    • init(seed, x): Returns initial parameters of the NN
    • apply(params, x): Pure function to apply the NN
       
  • Training the Model: Use jax.grad to compute gradients and Optax optimizers to update parameters

Now You Try it!

We will be using this notebook 

https://bit.ly/3LaLHq3

Your goal: Building a regression model with a Mean Squared Error loss in JAX/Flax

def loss_fn(params, x, y):
  mse = (model.apply(params, x) - y)**2
  return jnp.mean(mse)

Raise your hand when you reach the cluster mass prediction plot

First attempt with an MSE loss

class MLP(nn.Module):
  @nn.compact
  def __call__(self, x):
    x = nn.relu(nn.Dense(128)(x))
    x = nn.relu(nn.Dense(128)(x))
    x = nn.tanh(nn.Dense(64)(x))
    x = nn.Dense(1)(x)
    return x
 
def loss_fn(params, x, y):
  prediction = model.apply(params, x)
  return jnp.mean( (prediction - y)**2 )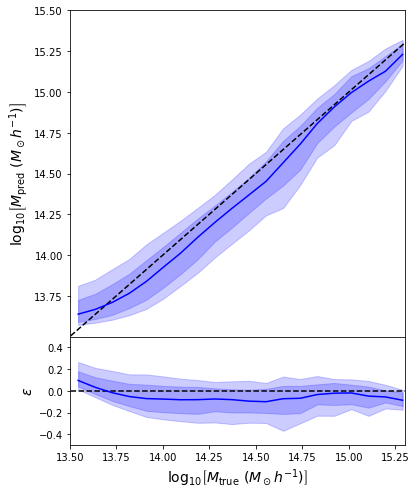
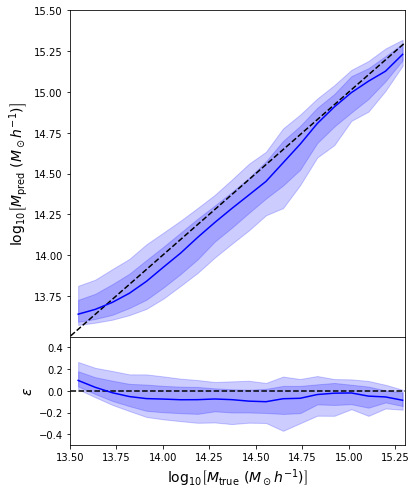
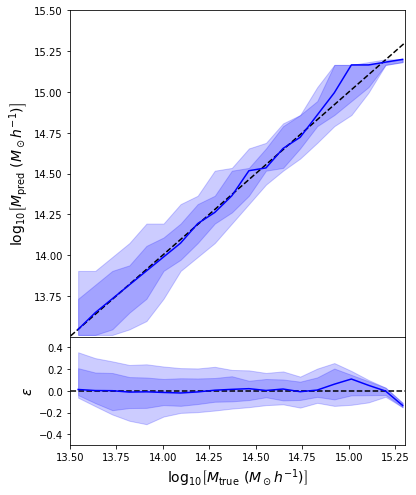
  • Simple Dense network  using 14 features derived from galaxy positions and velocity information
     
  • We see that the predictions are biased compared to the true value of the mass... Not good.

What is going on???

We need a new tool to go probabilistic

Tensorflow Probability

import jax
import jax.numpy as jnp
from tensorflow_probability.substrates import jax as tfp
tfd = tfp.distributions

### Create a mixture of two scalar Gaussians:
gm = tfd.MixtureSameFamily(
  mixture_distribution=tfd.Categorical(
                 probs=[0.3, 0.7]),
  components_distribution=tfd.Normal(
                 loc=[-1., 1],      
                 scale=[0.1, 0.5]))

# Evaluate probability
gm.log_prob(1.0)

Let's build a Conditional Density Estimator with TFP

class MDN(nn.Module):
  num_components: int

  @nn.compact
  def __call__(self, x):
    x = nn.relu(nn.Dense(128)(x))
    x = nn.relu(nn.Dense(128)(x))
    x = nn.tanh(nn.Dense(64)(x))

    # Instead of regressing directly the value of the mass, the network
    # will now try to estimate the parameters of a mass distribution.
    categorical_logits = nn.Dense(self.num_components)(x)
    loc = nn.Dense(self.num_components)(x)
    scale = 1e-3 + nn.softplus(nn.Dense(self.num_components)(x))

    dist =tfd.MixtureSameFamily(
        mixture_distribution=tfd.Categorical(logits=categorical_logits),
        components_distribution=tfd.Normal(loc=loc, scale=scale))
    
    # To make it understand the batch dimension
    dist =  tfd.Independent(dist)
    
    # Returns a distribution !
    return dist

Now you try it!

Your goal: Implement a Mixture Density Network in JAX/Flax/TFP, and use it to  get unbiased mass estimates.

When everyone is done, we will discuss the results.

def loss_fn(params, x, y):
  q = model.apply(params, x)
  return jnp.mean( - q.log_prob(y[:,0]) )

Second attempt: Probabilistic Modeling

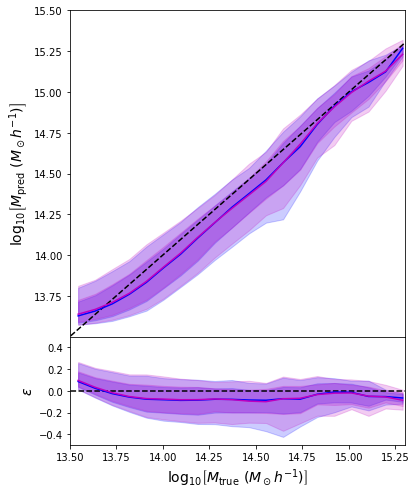
  • Same Dense network but now using a Mixture Density output.
     
  • Using the mean of the predicted distribution as our mass estimate: We see the exact same behaviour
    What am I doing wrong???

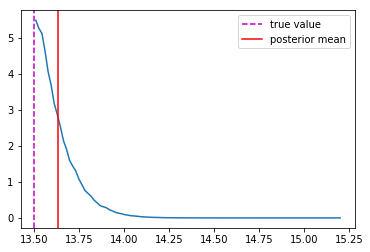
Accounting for Implicit Prior

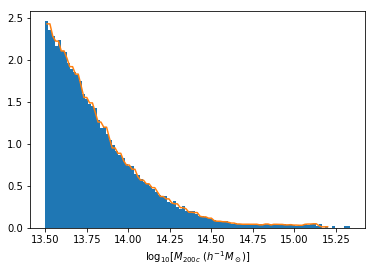
Distribution of masses in our training data

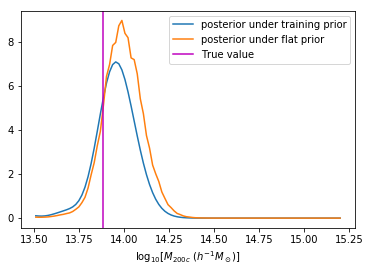
q(M_{200c} | x ) \propto \frac{\tilde{p}(M_{200c})}{p(M_{200c})} p(M_{200c} | x)

We can reweight the predictions for a desired prior

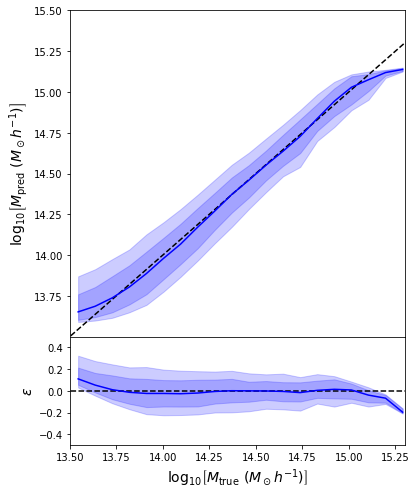
Last detail, use the mode instead of the mean posterior

Takeaway Message

  • Using a model that outputs distributions instead of scalars is always better!

     
  • It's 2 lines of TensorFlow Probability

     
  • Careful about interpreting these distributions as a Bayesian posterior, the training set acts as an Interim Prior, not necessarily matching your Bayesian prior.
    => Connection with proper Simulation Based Inference by Neural Density Estimation

A brief Mention of How to Model Epistemic Uncertainties

A Quick reminder

From this excellent tutorial: 

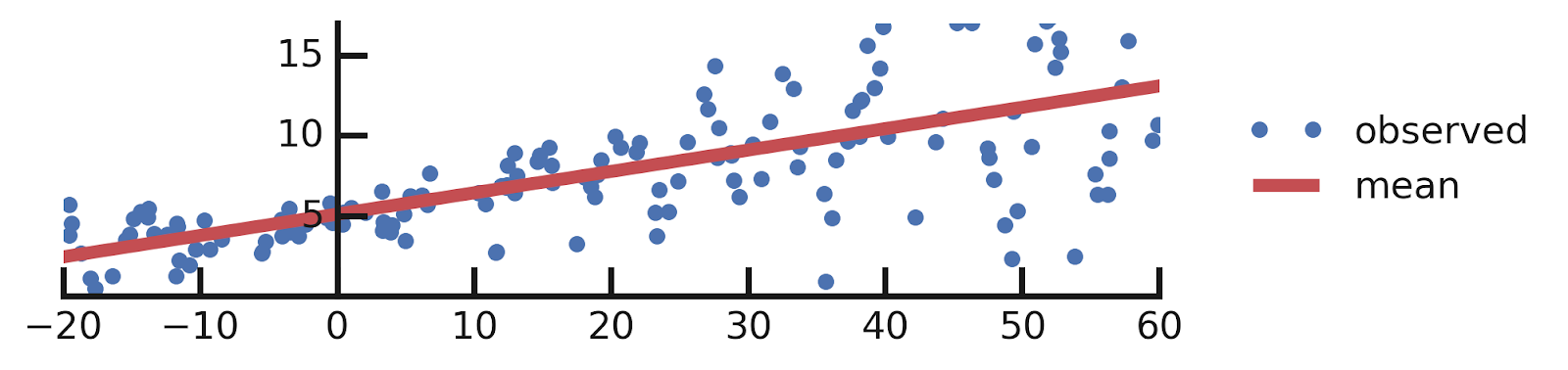
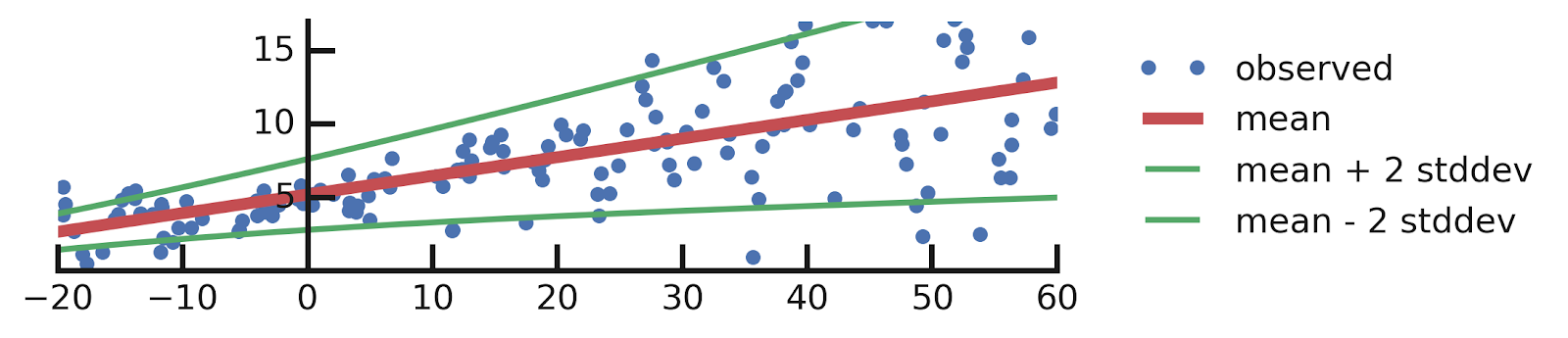
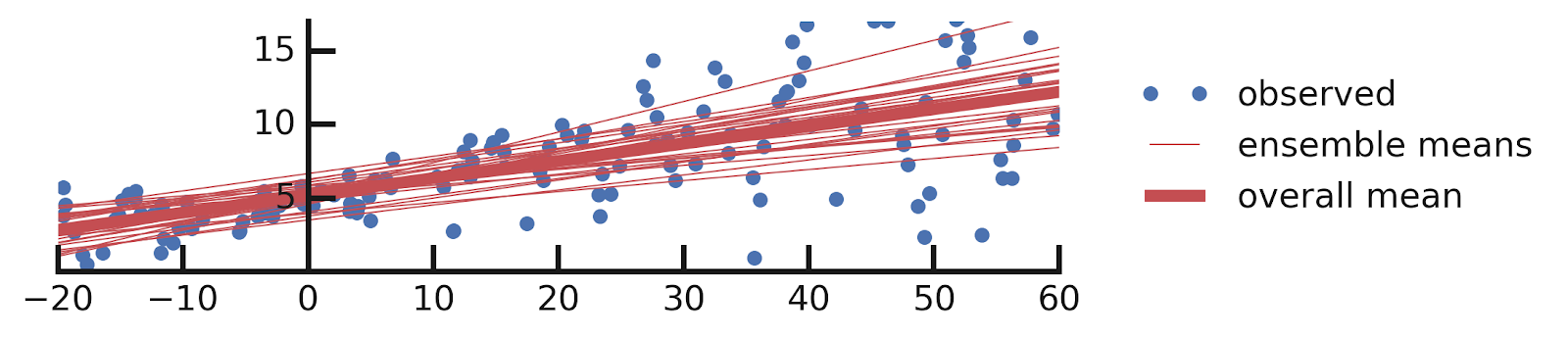
  • Linear regression

     
  • Aleatoric Uncertainties

     
  • Epistemic Uncertainties

     
  • Epistemic+ Aleatoric Uncertainties
\hat{y} = a x
\hat{y} \sim \mathcal{N}(a x, \sigma^2)
\hat{y} = w x \quad w \sim p(w | \{x_i, y_i\})
\hat{y} \sim \mathcal{N}(w x, \sigma^2) \\ w, \sigma \sim p(w, \sigma | \{x_i, y_i\})

The idea behind Bayesian Neural Networks

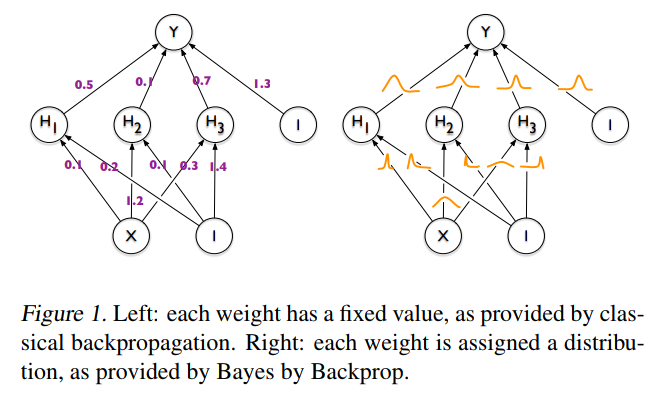
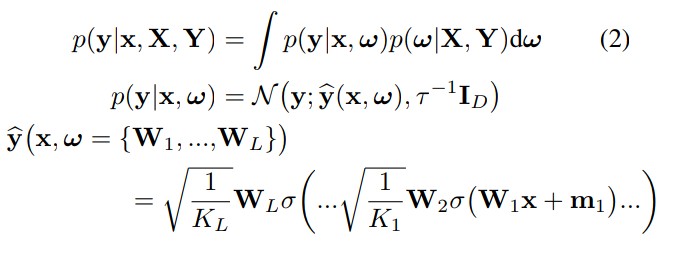
Given a training set  D = {X,Y}, the predictions from a Neural Network can be  expressed as:

Weight Estimation by Maximum Likelihood

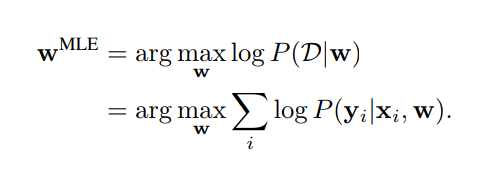
Weight Estimation by Variational Inference

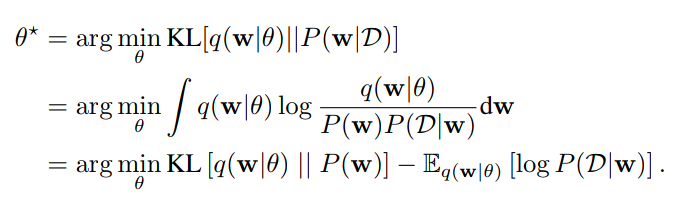
A first approach to BNNs:
Bayes by Backprop (Blundel et al. 2015)

  • Step 1: Assume a variational distribution for the weights of the Neural Network


     
  • Step 2: Assume a prior distribution for these weights


     
  • Step 3: Learn the parameters  of the variational distribution by minimizing the ELBO

 

 

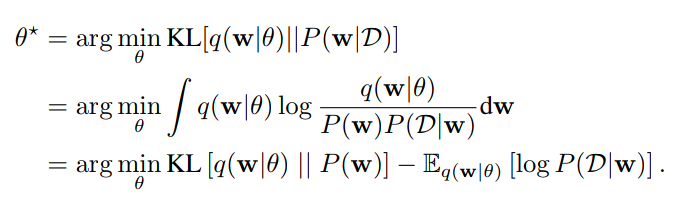
q_\theta(w) = \mathcal{N}( \mu_\theta, \Sigma_\theta )
p(w) = \mathcal{N}(0, I)

What happens in practice

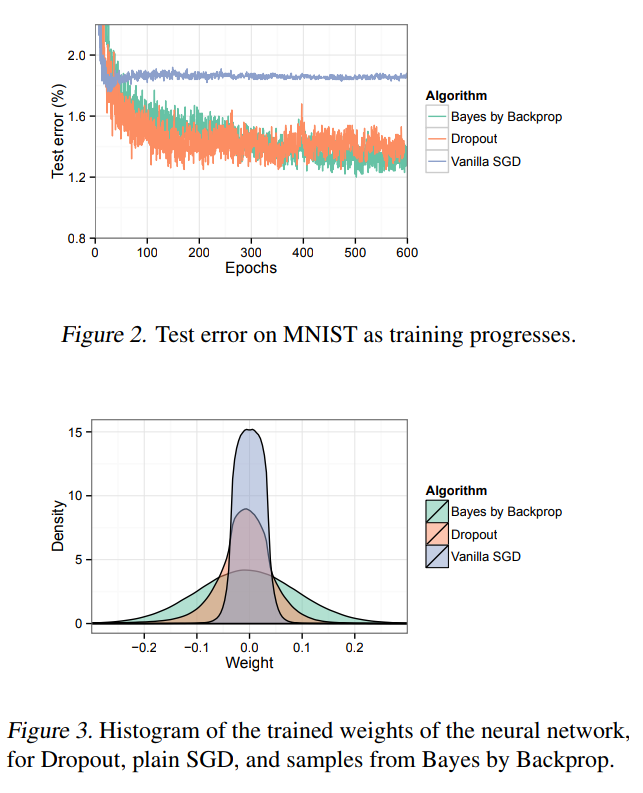
TensorFlow Probability implementation

A different approach:
Dropout as a Bayesian Approximation (Gal & Ghahramani, 2015)

Quick reminder on dropout
 

Hinton 2012, Srivastava 2014

Variational Distribution of Weights under Dropout

  • Step 1: Assume a Variational Distribution for the weights



     
  • Step 2: Assume a Gaussian prior for the weights, with "length scale" l
     
  • Step 3: Fit the parameters of the variational distribution by optimizing the ELBO

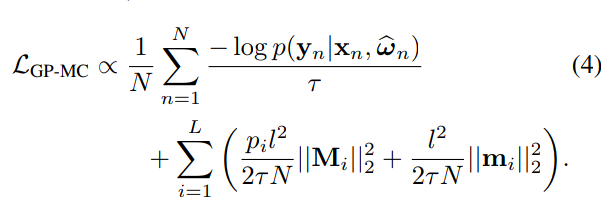
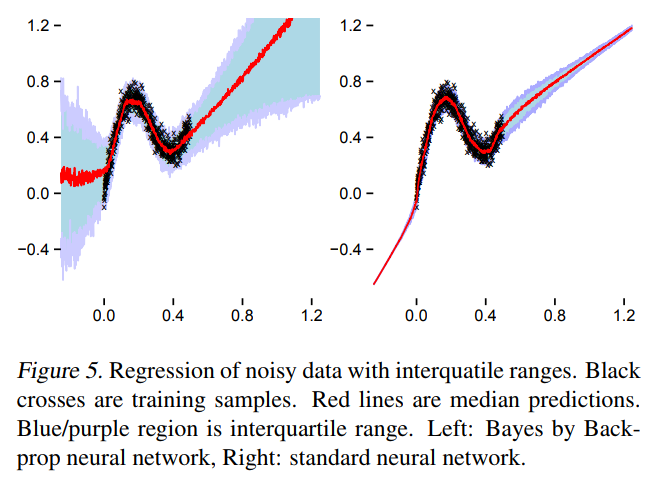
Example

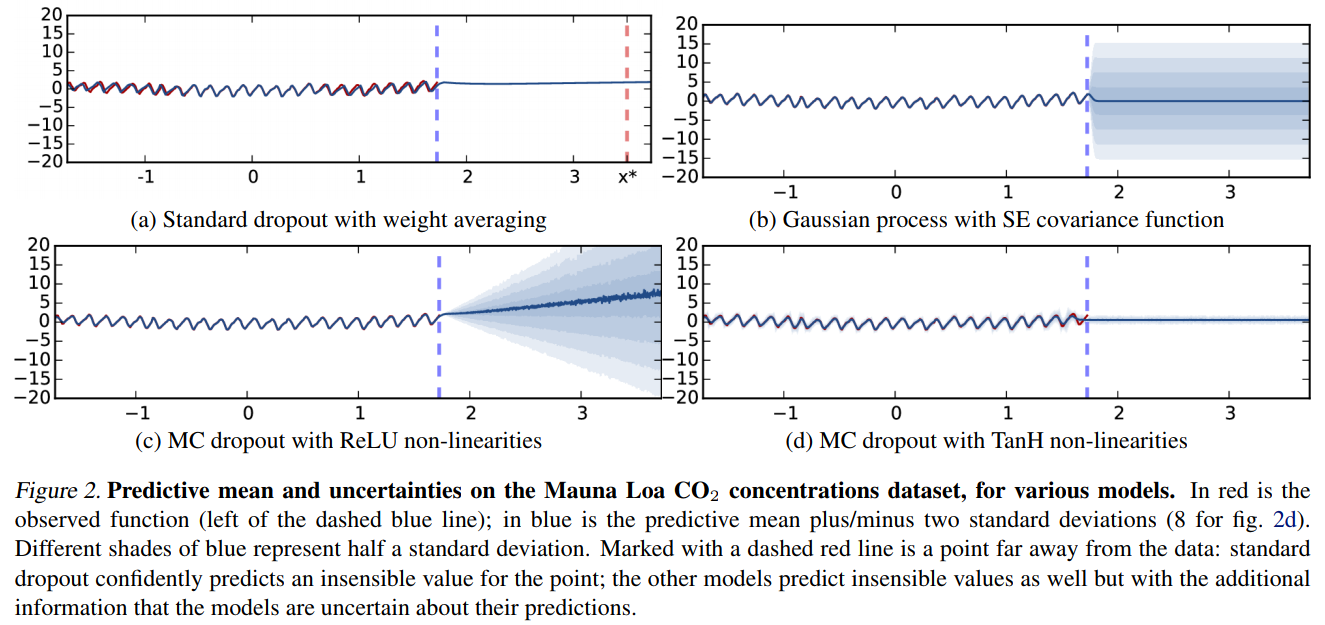
These are not the only methods

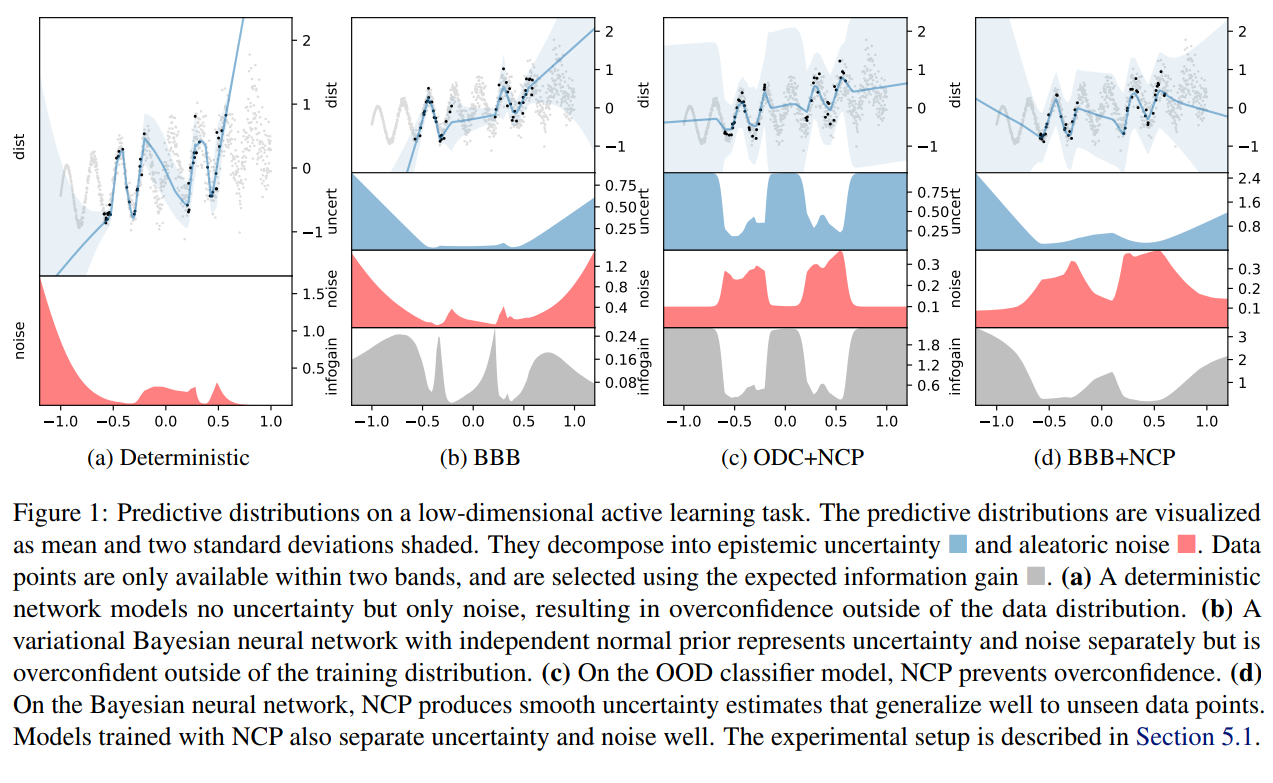
Takeaway message on Bayesian Neural Networks

  • They give a practical way to model epistemic uncertainties, aka unknowns unknows, aka errors on errors
     
  • Be very careful when interpreting their output distributions, they are Bayesian posterior, yes, but under what priors?






     
  • Having access to model uncertainties can be used for active sampling

Solution Notebook

here

Bonus Notebook Implementing a Normalizing Flow

here

Introduction to Probabilistic Learning in JAX

By eiffl

Introduction to Probabilistic Learning in JAX

Probabilistic Learning lecture at Kavli IPMU, April 2023

  • 420

More from eiffl

  • Multimodal PreTraining for Scientific Data - Berkeley, Oct 24
    eiffl
    61
  • Multimodal PreTraining for Scientific Data - Paris, Oct 24
    eiffl
    88
  • Multimodal PreTraining for Scientific Data - Oct 24
    eiffl
    150
  • Towards Multidisciplinary Scientific Foundation Models
    eiffl
    169