Bilgisayar grafikleri

Faruk CAN

04.01.15

Lütfen web sitemi ziyaret etmeyi unutmayın.

Konular arasında ilerlemek için sağa,

Bir konu hakkında ayrıntı için aşağı,

doğru ilerlemeniz gerekir

http://farukcan.net

Belge Sürümü : 1.00

Son Güncelleme: 01/15

Bilgisayar Grafiklerin Gelişimi

Vektörler

• Bir büyüklüğü ve yönü ifade eden matrislerdir
• 2,3 ve 4 boyutlu olabilir
• Vektörler konum belirtmez.
• Fakat konum vektör ile belirtilebilir.
• Bilgisayarda matrislerle (2B Array) ifade edilir

//
//        vec2d CLASS by farukcan
//            vektör sınıfı ve fonksiyonlarıdır
function vec2d(x,y){
  this.x = x;
  this.y = y;

  this.add = function(v){ // a.add(v) => a-> = ->a + ->b
    this.x+=v.x;
    this.y+=v.y;
    return this;
  }
  this.sub = function(v){
    this.x-=v.x;
    this.y-=v.y;
    return this;
  }
  this.norm = function(){
    return Math.sqrt(this.x*this.x+this.y*this.y);
  }
  this.skaler = function (k) { // ->a = k.->a
    this.x*=k;
    this.y*=k;
    return this;
  }
}
function v2(x,y){ // vec2d'nın hızlı oluşturucusu
  return new vec2d(x,y);
}

function dot2vec(a,b){ // ->A & ->B => AB-> = dot2vec(A,B)
  var e = b;
  return vec_sub(b,a);
}

function vec_sub(a,b){
  return new vec2d(a.x-b.x,a.y-b.y);
}

function vec_add(a,b){
  return new vec2d(a.x+b.x,a.y+b.y);
}

function vec_skaler (k,v) {
  return new vec2d(k*v.x,k*v.y);
}

function vec_paralel(a,b){ // birbirlerin katıysa bunlar paraleldir
  if((a.x/b.x)==(a.y/b.y))
    return true;
  return false;
}

function vec_carp_skaler(a,b){ // skaler : iç çarpım A-> * B-> = |A| * |B| * cosX
  return a.x*b.x+a.y*b.y;
}

function vec_cos(a,b){
  return vec_carp_skaler(a,b)/a.norm()/b.norm();
}

function vec_birim(v){
  var n = v.norm();
  return v2(v.x/n,v.y/n);
}

function vec_izdusum(a,b){ // A vektörünün B üzerine iz düşümüdür B'nın birim vek @@ projeksiyonu diyede adlandırılabilir
// b'nin birim vektörünün ab skaler capımı ile çarpımıdır.
return vec_birim(b).skaler(vec_izdusum_norm(a,b));
}

function vec_izdusum_norm(a,b){ // A vektörünün B üzerine iz düşümüdür (A->*B->) / |B|
  return vec_carp_skaler(a,b)/b.norm();
}
//
// ------
//

Vektörün ifadesi

AB = A => B
A = 0A

2 boyutlu
| x |
| y |

3 boyutlu
| x |
| y |
| z |

Vektörün Normu (Uzunluğu)

Vektörün sonun başlangıç noktası uzaklığıdır ||x|| şeklinde ifade edilir

  this.norm = function(){
    return Math.sqrt(this.x*this.x+this.y*this.y);
  }

Vektörlerin paralelliği

Aynı yöne veya birbirine zıt yöne bakan vektörler paraleldir. Ve bunların şiddetinin birimleri orasında oran vardır

function vec_paralel(a,b){ // birbirlerin katıysa bunlar paraleldir
  if((a.x/b.x)==(a.y/b.y))
    return true;
  return false;
}

Birim vektör

Normu daima 1 olan vektörlerdir.

Sadece yön ifade etmek için kullanılır

function vec_birim(v){
  var n = v.norm();
  return v2(v.x/n,v.y/n);
}

Vektörde

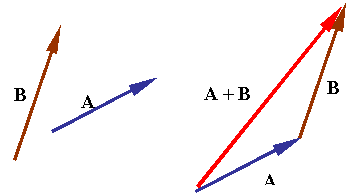
toplama çıkarma

function vec_sub(a,b){
  return new vec2d(a.x-b.x,a.y-b.y);
}

function vec_add(a,b){
  return new vec2d(a.x+b.x,a.y+b.y);
}

Vektörün bir sayıyla skaler çarpımı

vektörün şiddetini/uzunluğunu o sayı ile orantılı arttırır.

function vec_skaler (k,v) {
  return new vec2d(k*v.x,k*v.y);
}

2 Vektörün Skaler Çarpımı (dot product)

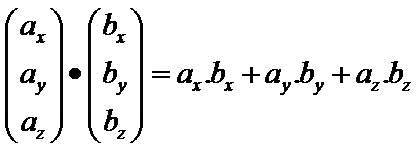
• Uzunluklukların aralarındaki açının cos u ile çarpımı ile bulunur.(veya)
• Matrislerin A^T * B si ile ile bulunur. Yani (İlkinin transponuyla ikincisinin çarpımı)(veya)
• Değerler(x,y,z,h)'lerin çarpılıp toplanması ile bulunur

function vec_carp_skaler(a,b){
  return a.x*b.x+a.y*b.y;
}

İz düşüm vektörü

function vec_izdusum(a,b){ 
// A vektörünün B üzerine iz düşümüdür B'nın birim vek @@ projeksiyonu diyede adlandırılabilir
// b'nin birim vektörünün ab skaler capımı ile çarpımıdır.
return vec_birim(b).skaler(vec_izdusum_norm(a,b));
}

function vec_izdusum_norm(a,b){ 
// A vektörünün B üzerine iz düşümüdür (A->*B->) / |B|
  return vec_carp_skaler(a,b)/b.norm();
}

Matrisler

Satır ve sutunlarından oluşan 2 boyutlu değer dizisidir

Matriste çarpma

Vektör Matrisleri ile

• 1 Vektörle => Nokta
• 2 Vektörle => Dogru
• 3 Vektörle => Yüzey
• n Vektörle => Cisim

oluşturulabilir/ifade edilebilir

Vektör dizileri

(3,5) => 2B Nokta

(3,3,5) => 3B nokta

2B Doğru

3,5

6,8

2B Yüzey

3,5

6,8

7,5

Homojenlik

ötemelemeye imkan tanımak için eklenen ek satır/değerdir. Bir konumu farklı şekilde ifade etmeye imkan tanır. Standart değeri 1'dir. Kullanılırkende 1 olmalıdır

2B

homojen değil

X

y

homojen

x

y

1

3B

homojen değil

X

y

z

homojen

x

y

z

1

Dönüşüm / Transformasyon

• Translation -Öteleme/Taşıma
• Scale - Boyutlandırma & Yansıtma
• Rotation - Döndürme
• Shear - Yamultma

Dönüşüm bir vektör matrisinin, o dönüşüme karşılık gelen matris ile çarpımı ile olur

2B Transformasyonlar

Öteleme

Bir noktayı hareket ettirmektir. (homojen noktalarda geçirlidir)

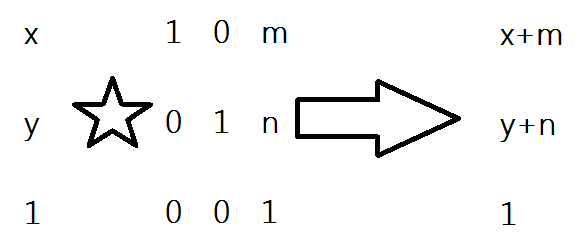
Scale - Boyutlandırma

Rotate - Döndürme

cT = cos(T)

sT = sin(T)

Shearing - Yamultma

?

3B Dönüşümler

3B Döndürme

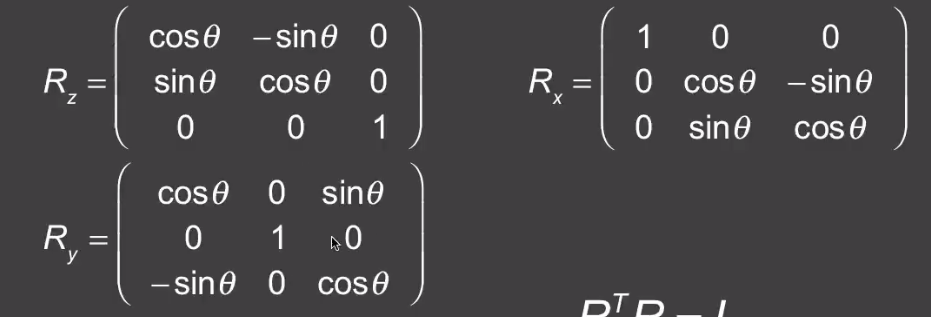
2B deki gibi yer değişme özelliğini sahip değildir.

R1 * R2 != R2 * R1

yani ilk x sonra yye döndürmekle ilk yye sonra xe döndürmek aynı şeyler değil

3B Öteleme

Öteleme+Döndürme != Döndürme+Ötelme

Çünkü öteleme Toplama işlemine karşılık gelir.

P' = (TR)P =  RP + T

Ötemele Transformansyon matrisi

1    0    0    TX
0    1    0    TY
0    0    1    TZ
0    0    0    0