Constante de Stefan-Boltzmann
Ilya Orson Sandoval Cárdenas
Fernando Arturo Araiza Sixtos
El Cuerpo Negro
- Es un objeto ideal que absorbe la radiación incidente sin importar la frecuencia o el ángulo de incidencia.
- En equilibrio termodinámico es necesario que también radie en todas las frecuencias (radiación de cuerpo negro).
- Su estudio conecta la termodinámica, la física estadística y la mecánica cuántica.
El éxito de Planck
La energía emitida por un cuerpo negro por unidad de tiempo y área depende sólo de la temperatura.
K = \sigma T^4
\sigma = \frac{\pi ^2 k^4}{15(\hbar c)^3}
\sigma \approx 5.670367(13)\times 10^{-8} J/s m^2 K^4
Con ayuda de la física estadística se deduce la siguiente expresión:
Entonces esperamos obtener algo cercano al siguiente valor.
Desarrollo experimental
- Se usaron varios alambres de cobre, a los que se les quitó el esmalte y se les llenó de hollín, en total se tomaron datos para 9 alambres.
- Se ató un extremo al gancho conductor de la tapa superior del tubo de vacío y el otro a una pesa en contacto eléctrico con la tapa inferior.
- Se midió la longitud y diámetro del alambre
- Se hizo vacío dentro del tubo.
- Se conectaron las tapas a una fuente y un par de multímetros.
\ell
d
Arreglo experimental
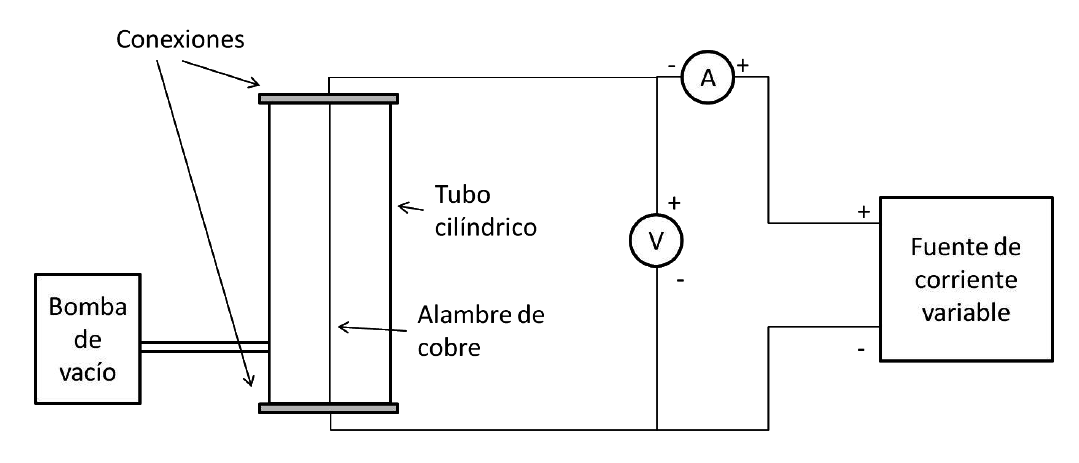
Toma de datos
- Se hizo variar la corriente y la diferencia de potencial hasta que el alambre alcanzara su temperatura de fusión T=1357,77 K.
- Se grabó en video los dos multímetros para capturar el momento exacto en que ésto pasara.
- Se calculó la constante usando la ecuación:
\sigma = \frac{VI}{\pi d\ell T^4}
Mediciones y Resultados
| Diámetro (mm) | Longitud (cm) | Voltaje (V) | Corriente (A) | Constante de Stefan |
|---|---|---|---|---|
| 0.142 | 27.4 | 5.17 | 3.35 | 4.160E-8 |
| 0.150 | 27.1 | 3.68 | 3.37 | 2.8573E-8 |
| 0.140 | 27.0 | 5.51 | 3.58 | 4.8875E-8 |
| 0.150 | 27.0 | 5.13 | 3.14 | 3.7251E-8 |
| 0.152 | 27.3 | 5.13 | 3.45 | 3.9946E-8 |
| 0.140 | 27.6 | 4.76 | 3.62 | 4.1766E-8 |
| 0.145 | 27.1 | 4.72 | 3.46 | 3.8947E-8 |
| 0.145 | 27.3 | 5.19 | 3.59 | 4.4083E-8 |
| 0.142 | 27.4 | 4.76 | 3.62 | 4.1478E-8 |
Resultado Final
Se tomó videos para nueve alambres y se obtuvo la siguiente constante:
\sigma=(4.029\pm 0.55)\times 10^{-12}\frac{W}{m^2\cdot K^4}
Comparando con el valor esperado, tenemos un error porcentual de 28.95%
Conclusiones
- El motivo por el que se obtuvieron valores menores que el real se debe principalmente a que los alambres usados no son cuerpos negros reales.
- Absorben menos radiación electromagnética que éstos (y por ende, también emiten menos).
- La toma de datos se debía hacer en un proceso cuasiestático, lo cuál no pudo ser posible debido a que los multímetros varíaban demasiado.
Copy of Stefan-Boltzmann
By Fernando Arturo Araiza Sixtos
Copy of Stefan-Boltzmann
Laboratorio de Física Contemporánea I: Determinar la constante de Stefan-Boltzmann por un método indirecto.
