Existencia del Fotón

Fernando Arturo Araiza Sixtos

Ilya Orson Sandoval Cárdenas

¿Es necesario?

  • Efecto fotoeléctrico
  • Dispersión  de Compton
  • Radiación de cuerpo negro

Aunque muchos fenómenos se explican fácilmente suponiendolo, esto no lo demuestra. 

Por ejemplo:

¿Cómo se prueba?

Utilizamos la indivisibilidad del fotón.

Divisor de Haz

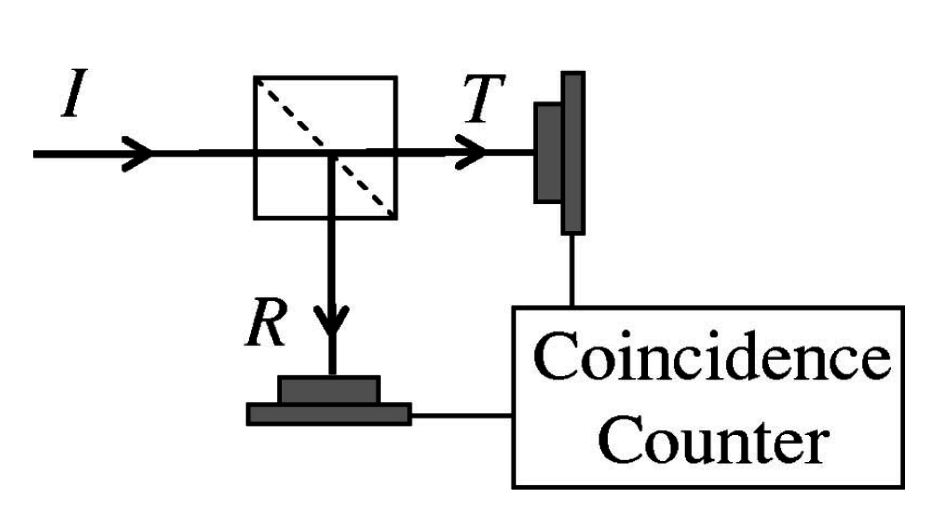
Text

Es necesario poder registrar fotones individuales.

Coherencia Temporal de Segundo Orden

g^{(2)} = \frac{\langle I_T(t+\tau)I_R(t)\rangle}{\langle I_T(t+\tau) \rangle \langle I_R(t) \rangle}
g(2)=⟨IT(t+τ)IR(t)⟩⟨IT(t+τ)⟩⟨IR(t)⟩g^{(2)} = \frac{\langle I_T(t+\tau)I_R(t)\rangle}{\langle I_T(t+\tau) \rangle \langle I_R(t) \rangle}

Nos interesan las mediciones simultaneas

g^{(2)}(0) = \frac{\langle I_T(t)I_R(t)\rangle}{\langle I_T(t) \rangle \langle I_R(t) \rangle}
g(2)(0)=⟨IT(t)IR(t)⟩⟨IT(t)⟩⟨IR(t)⟩g^{(2)}(0) = \frac{\langle I_T(t)I_R(t)\rangle}{\langle I_T(t) \rangle \langle I_R(t) \rangle}
\tau = 0
τ=0\tau = 0

Para campos clásicos

g^{(2)}(0) \geq 1
g(2)(0)≥1g^{(2)}(0) \geq 1

Para campos cuánticos

g^{(2)}(0) = 0
g(2)(0)=0g^{(2)}(0) = 0

¿Cómo asegurar que se mide sólamente un fotón?

Para realizar con éxito el experimento se usa el método de conversión descendente paramétrica (CDP), método que tiene las ventajas de ser bastante simple, reduce costos, y aumenta los conteos. En este método, un fotón de una sóla frecuencia es convertido en dos fotones de menor frecuencia.

Conversión Descendente Paramétrica (CDP)

El haz entrante llega con una frecuencia angular         y los dos haces resultantes tienen frecuencias angulares                   respectivamente, por conservación de energía se tiene que

\omega_p
ωp\omega_p
\omega_s, \omega_i
ωs,ωi\omega_s, \omega_i
\hbar\omega_p =\hbar\omega_s + \hbar\omega_i \Rightarrow \omega_p =\omega_s +\omega_i
ℏωp=ℏωs+ℏωi⇒ωp=ωs+ωi\hbar\omega_p =\hbar\omega_s + \hbar\omega_i \Rightarrow \omega_p =\omega_s +\omega_i

La conservación de momento es equivalente a igualar las fases, lo que nos da la condición que deben cumplir los vectores de onda

\vec{\kappa}_p = \vec{\kappa}_i + \vec{\kappa}_s
κ⃗p=κ⃗i+κ⃗s\vec{\kappa}_p = \vec{\kappa}_i + \vec{\kappa}_s

Las frecuencias y vectores de onda no son independientes entre ellos, y están relacionados mediante la relación de dispersión

\kappa_p=\frac{n_p(\omega_p)\omega_p}{c}
κp=np(ωp)ωpc\kappa_p=\frac{n_p(\omega_p)\omega_p}{c}

Experimento

Al pasar por el DCC el haz es dividido en dos haces, uno se usa como gate. La detección de un fotón en G nos indica que hay otro fotón en el otro haz, el cual se hace pasar a través de un divisor de haz para medir en T y R.

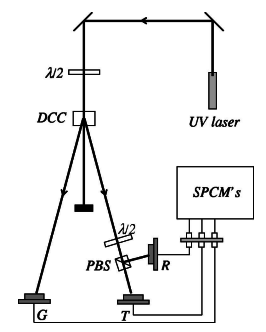
Arreglo experimental

Resultados

  • La mínima escala de tiempo del detector: 1bin(81ps)
  • Se registraron las incidencias en ventanas de tiempo de 62,124 y 248 bins (5,10 y 20 ns).
  • Se utilizaron dos intensidades: 0.323 y 14.94mW
  • Con menor intensidad la medición duró 30s.
  • Con mayor intensidad duró 1min.

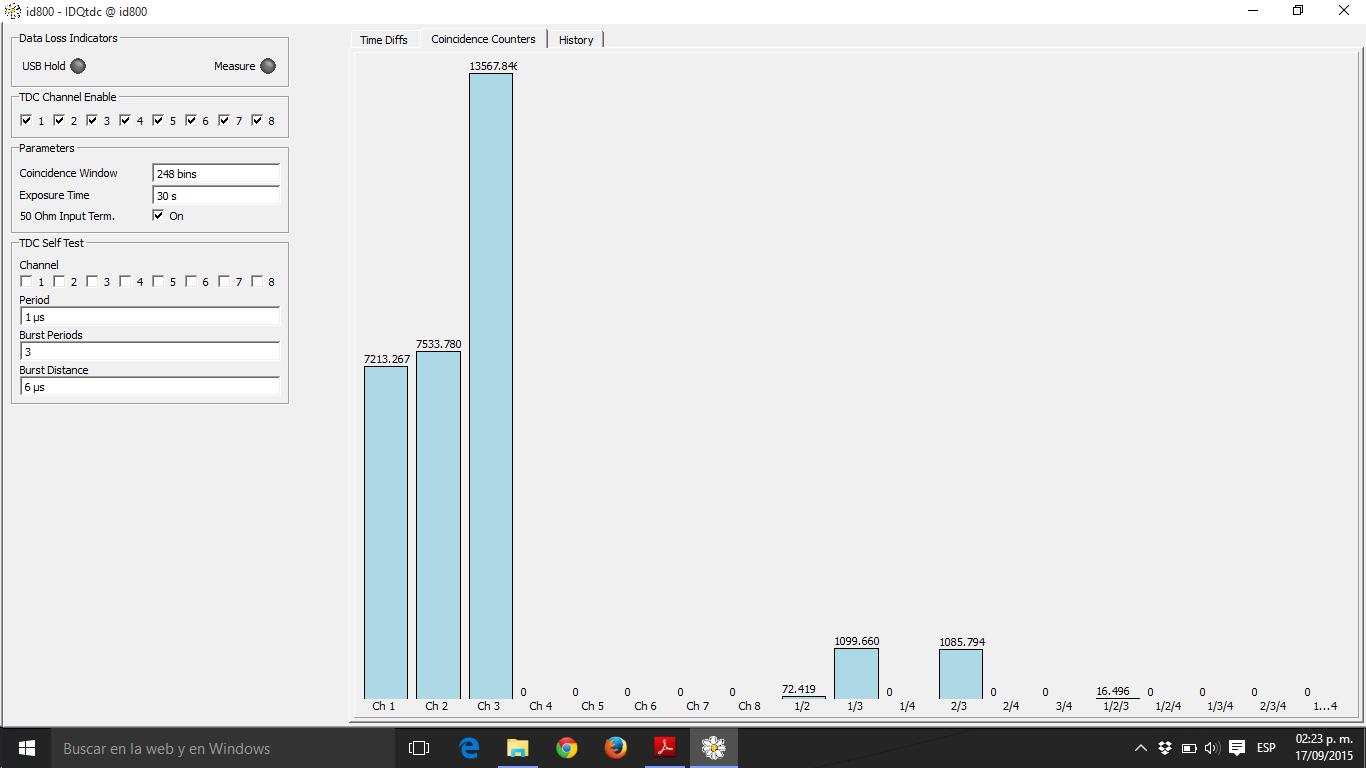
Ejemplo de medición

Número de bins Correlación promedio Desviaciónes de la unidad
62 0.0011(5) 2283
124 0.0019(4) 2685
248 0.006(1) 1015
Número de bins Correlación promedio Desviaciónes de la unidad
62 0.03866(2) 3875
124 0.087(1) 691
248 0.182(4) 209

Intensidad = 14.94mW

Intensidad = 0.323mW

¡Existe el fotón!

Copy of Existencia del Fotón

By Fernando Arturo Araiza Sixtos

Made with Slides.com

Copy of Existencia del Fotón

Laboratorio Rotativo

  • 827

More from Fernando Arturo Araiza Sixtos