Minimizing movements schemes
with general movement limiters
Flavien Léger
joint works with Pierre-Cyril Aubin-Frankowski,
Gabriele Todeschi, François-Xavier Vialard
What I will present
Theory for minimizing movement schemes in infinite dimensions and in nonsmooth (nondifferentiable) settings, with a movement limiter given by a general cost function.
Main motivation: optimization on a space of measures \(\mathcal{P}(M)\):
minimize \(E\colon \mathcal{P}(M)\to\mathbb{R}\cup\{+\infty\}\)
Typical scheme:
\mu_{n+1}\in\operatorname*{argmin}_{\mu\in\mathcal{P}(M)} E(\mu)+\frac{1}{2\tau}D(\mu,\mu_n)
where \(D(\mu,\nu)=\)
transport cost: \(W_2^2(\mu,\nu)\), \(\mathcal{T}_c(\mu,\nu)\),...
Bregman divergence: \(\operatorname{KL}(\mu,\nu)\),...
Csiszár divergence: \(\int_M (\sqrt{\mu}-\sqrt{\nu})^2\),...
...
What I will present
Theory for minimizing movement schemes in infinite dimensions and in nonsmooth (nondifferentiable) settings, with a movement limiter given by a general cost function.
1. Formulations for implicit and explicit schemes in a general setting
2. Theory for rates of convergence based on convexity along specific paths, and generalized “\(L\)-smoothness” (“\(L\)-Lipschitz gradients”) for explicit scheme
Implicit scheme
\inf_{y\in Y}D(x,y)=0
Minimize \(E\colon X\to\mathbb{R}\cup\{+\infty\}\), where \(X\) is a set (set of measures, metric space...).
Use \(D\colon X\times Y\to\mathbb{R}\cup\{+\infty\}\), where \(Y\) is another set (often \(X=Y\)).
\begin{aligned}
x_n & \in\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n)\\
y_{n+1}&\in\operatorname*{argmin}_{y\in Y} D(x_n,y)
\end{aligned}
Algorithm
(Implicit scheme)
Rem: formulated as an alternating minimization
Motivations for general \(D(x,y)\):
Implicit scheme
- \(D(x,y)\) tailored to the problem
- Gradient flows “\(\dot x(t)=-\nabla E(x(t))\)”
⏵ Define gradient flows in nonsmooth, metric settings: \(\displaystyle D=\frac{d^2}{2\tau}, \tau\to 0\)
⏵ \(D(x,y)\) as a proxy for \(d^2(x,y)\) (same behaviour on the diagonal):
(Ambrosio–Gigli–Savaré ’05)
(De Giorgi ’93)
Toy example: \(\dot x(t)=-\nabla^2u(x(t))^{-1}\nabla E(x(t))\), \(u\colon \R^d\to\R\) strictly convex
Two approaches:
\left\{\begin{aligned}
D(x,y)&=\frac{d^2(x,y)}{2\tau},\\
D(x,y)&=\frac{u(x)-u(y)-\langle\nabla u(y),x-y\rangle}{\tau}
\end{aligned}
\right.
\(d=\) distance for Hessian metric \(\nabla^2 u\)
Alternating minimization
Given \(\Phi\colon X\times Y\to\mathbb{R}\cup\{+\infty\}\) to minimize, define
\begin{aligned}
x_n & \in\operatorname*{argmin}_{x\in X}\Phi(x,y_n)=\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n)\\
y_{n+1}&\in\operatorname*{argmin}_{y\in Y} \Phi(x_n,y)=\operatorname*{argmin}_{y\in Y}D(x_n,y)
\end{aligned}
Examples of AM: Sinkhorn, Expectation–Maximization, Projections onto convex set, SMACOF for multidimensional scaling...
E(x)=\inf_{y\in Y}\Phi(x,y),
Then alternating minimization of \(\Phi\iff\) implicit method with \(E\) and \(D\):
D(x,y)=\Phi(x,y)-E(x)
Explicit minimizing movements: warm-up
Two steps:
1) majorize: find the tangent parabola (“surrogate”)
2) minimize: minimize the surrogate
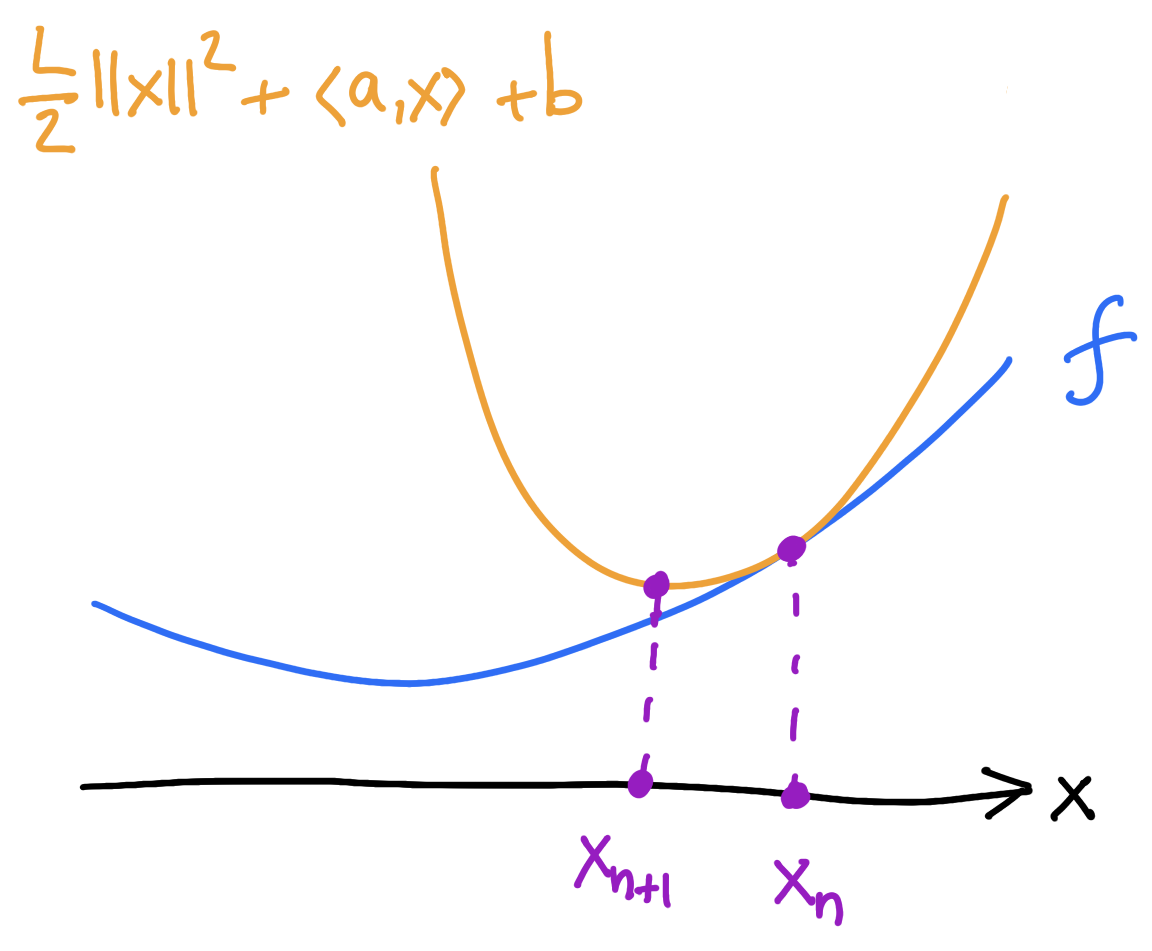
\[x_{n+1}=x_n-\frac{1}{L}\nabla E(x_n)\]
\(E\colon \mathbb{R}^d\to\mathbb{R}\)
Gradient descent
“Nonsmooth” formulation of Gradient descent:
E
Warm-up question: how to formulate GD in a nonsmooth context? (ex: metric space)
Explicit minimizing movements: warm-up
Two steps:
1) majorize: find the tangent parabola (“surrogate”)
2) minimize: minimize the surrogate
If \(E\) is \(L\)-smooth (\(\nabla^2 E\leq L I_{d\times d}\)) then it sits below the surrogate:
\[E(x)\]
\[\leq\]
\[E(x_n)+\langle\nabla E(x_n),x-x_n\rangle+\frac{L}{2}\lVert x-x_n\rVert^2\]
E
\[x_{n+1}=x_n-\frac{1}{L}\nabla E(x_n)\]
Explicit minimizing movements: c-concavity
E(x)
D\colon X\times Y\to\mathbb{R}\cup\{+\infty\}
E\colon X\to\mathbb{R}\cup\{+\infty\}
\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)
D(x,y)+h(y)
=\inf_{y\in Y}
Definition.
\(E\) is c-concave if
generalizes “\(L\)-smoothness”
Abstract setting:
Smallest such \(h\) is the c-transform
\(h(y)=\sup_{x\in X}E(x)-D(x,y)\)
E(x)
\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)
D(x,y)+h(y)
=\inf_{y\in Y}
Definition.
\(E\) is c-concave if
E
E
c-concave
not c-concave
D(x,y)+h(y)
Explicit minimizing movements: c-concavity
Differentiable NNCC setting. Suppose that \(\forall x\in X,\exists y\in Y\): \(\nabla_x D(x,y)=\nabla E(x)\) and
\[\nabla^2 E (x) \leq \nabla^2_{xx}D(x,y).\]
Then \(E\) is c-concave.
Theorem.
(L–Aubin-Frankowski, à la Trudinger–Wang '06)
\(\exists h\colon Y\to\mathbb{R}\cup\{+\infty\}\)
Definition.
\(E\) is c-concave if
Explicit minimizing movements: c-concavity
E(x)
D(x,y)+h(y)
=\inf_{y\in Y}
Explicit minimizing movements
\begin{aligned}
y_{n+1}&\in\operatorname*{argmin}_{y\in Y}D(x_n,y)+h(y)\\
x_{n+1} & \in\operatorname*{argmin}_{x\in X}D(x,y_{n+1})
\end{aligned}
(majorize)
(minimize)
E
D\colon X\times Y\to\mathbb{R}\cup\{+\infty\}
E\colon X\to\mathbb{R}\cup\{+\infty\}
Algorithm.
(Explicit scheme)
Assume \(E\) c-concave.
(L–Aubin-Frankowski '23)
D(x,y)+h(y)
Explicit minimizing movements
\(X,Y\) smooth manifolds, \(D\in C^1(X\times Y)\), \(E\in C^1(X)\) c-concave
\begin{aligned}
-\nabla_{\!x} D(x_n,y_{n+1})&=-\nabla E(x_n)\\
\nabla_{\!x} D(x_{n+1},y_{n+1})&=0
\end{aligned}
Under certain assumptions, the explicit scheme can be written as
x_{n+1}-x_n=-\tau\nabla E(x_n)
D(x,y)=\frac{1}{2\tau}\lVert x-y\rVert^2
x_{n+1}=\exp_{x_n}(-\tau\nabla E(x_n))
D(x,y)=\frac{1}{2\tau}d_M^2(x,y)
\nabla u(x_{n+1})-\nabla u(x_n)=-\nabla E(x_n)
D(x,y)=u(x)-u(y)-\nabla u(y)(x-y)
x_{n+1}-x_n=-\nabla^2u(x_n)^{-1}\nabla E(x_n)
D(x,y)=u(y)-u(x)-\nabla u(x)(y-x)
More: nonsmooth mirror descent, convergence rates for Newton
2. Convergence rates
EVI and convergence rates
Definition.
\forall x\in X,\quad E(x_n)+D(x_n,y_n)+(1+\mu)D(x,y_{n+1})\leq E(x)+D(x,y_n)
(Csiszár–Tusnády ’84)
(L–Aubin-Frankowski ’23)
Evolution Variational Inequality (or five-point property):
(\mu\geq 0)
x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n), \quad y_{n+1} \in\operatorname*{argmin}_{y\in Y} D(x_n,y)
If \((x_n,y_n)\) satisfy the EVI then
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0)}{n}
sublinear rates when \(\mu=0\)
exponential rates when \(\mu>0\)
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0,\mu)}{(1+\mu)^n-1}
Theorem.
(L–Aubin-Frankowski '23)
(Ambrosio–Gigli–Savaré ’05)
EVI
\forall x\in X,\quad E(x_n)+D(x_n,x_{n-1})\leq E(x)+D(x,x_{n-1})-(1+\mu)D(x,x_{n})
x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,x_{n-1})
Take \(X=Y\), \(D\geq 0\), \(D(x,x)=0\,\,\longrightarrow\,\, y_{n+1}=x_n\),
(\mu\geq 0)
⏵ EVI as a property of \(E\): \(\displaystyle \exists x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,x_{n-1})\) s.t.
x_n\in\operatorname*{argmin}_{x\in X}E(x)+D(x,x_{n-1})-(1+\mu)D(x,x_n)
⏵ Proving the EVI: find a path \(x(s)\) along which \(E(x)-\mu D(x,x_n)+D(x,x_{n-1})-D(x,x_n)\) is convex ( → local to global)
Ex: \(E\colon\R^d\to\R\) \(\frac{\mu}{\tau}\)-convex, \(D(x,y)=\frac{1}{2\tau}\lVert x-y\rVert^2\)
3. A synthetic formulation of nonnegative cross-curvature
Variational c-segments and NNCC spaces
⏵ \(s\mapsto (x(s),\bar y)\) is a variational c-segment if \(D(x(s),\bar y)\) is finite and
⏵ \((X\times Y,D)\) is a space with nonnegative cross-curvature (NNCC space) if variational c-segments always exist.
\(X, Y\) two arbitrary sets, \(D\colon X\times Y\to\mathbb{R}\cup\{\pm\infty\}\).
(1-s)[D(x(0),\bar y)-D(x(0),y)]+s[D(x(1),\bar y)-D(x(1),y)].
\forall y\in Y\!,\quad D(x(s),\bar y)-D(x(s),y)\leq
x(0)
x(1)
\bar y
Definition.
(L–Todeschi–Vialard '24)
Origins in regularity of optimal transport
(Ma–Trudinger–Wang ’05)
(Trudinger–Wang ’09)
(Kim–McCann ’10)
convexity of the set of c-concave functions
(Figalli–Kim–McCann '11)
Properties of NNCC spaces
Stable by products
Stable by quotients with “equidistant fibers”
(connect to: Kim–McCann '12)
(L–Todeschi–Vialard '24)
(finite) collection of NNCC spaces \((X^a\times Y^a,c^a)_{a=1..n}\),
$$\mathbf{X}=X^1\times\dots\times X^n,\quad \mathbf{Y}=Y^1\times\dots\times Y^n,\quad \mathbf{c}(\mathbf{x},\mathbf{y})=c^1(x^1,y^1)+\dots+c^n(x^n,y^n)$$
\((\mathbf{X}\times\mathbf{Y},\mathbf{c})\) is NNCC.
\(c\colon X\times Y\to [-\infty,+\infty], P_1\colon X\to\underline{X}\), \(P_2\colon Y\to\underline{Y}\) s.t. “equidistant fibers”
\inf_{y'\sim y}c(x,y')=\inf_{x'\sim x}c(x',y)\eqqcolon \underline{c}(P_1(x),P_2(y))
Then: \((X\times Y,c)\) NNCC \(\implies\) \((\underline{X}\times\underline{Y},\underline{c})\) NNCC
(connect to: Kim–McCann '12)
Quotients:
Products:
Properties of NNCC spaces
Metric cost \(c(x,y)=d^2(x,y)\) NNCC\(\implies\)PC
d^2(x(s),\bar y )\leq (1-s)d^2(x(0),\bar y)+s\,d^2(x(1),\bar y)-s(1-s)d^2(x(0),x(1))
(connect to: Ambrosio–Gigli–Savaré ’05)
(connect to: Loeper ’09)
(L–Todeschi–Vialard '24)
Application: transport costs
\mathcal{T}_c(\mu,\nu)=\inf_{\pi\in\Pi(\mu,\nu)}\int c(x,y)\,d\pi
“Proof.”
\((X\times Y,c)\) NNCC \(\implies\) \((\mathcal{P}(X)\times\mathcal{P}(Y),\mathcal{T}_c)\) NNCC
Ex: \(W_2^2\) on \(\mathbb{R}^n\), on \(\mathbb{S}^n\), OT with Bregman costs...
Variational c-segments \(\approx\) generalized geodesics
\(X,Y\) Polish, \(c\colon X\times Y\to\R\cup\{+\infty\}\) lsc
1. \((U,V)\mapsto \mathbb{E}\,c(U,V)=\int_\Omega c(U(\omega),V(\omega))\,d\mathbb{P}(\omega)\) is NNCC when \((X\times Y,c)\) is NNCC “product of NNCC”
2. \(\displaystyle\inf_{\operatorname{law}(U)=\mu}\mathbb{E}\,c(U,V)=\inf_{\operatorname{law}(V)=\nu}\mathbb{E}\,c(U,V)=\mathcal{T}_c(\mu,\nu)\) “equidistant fibers”
Theorem.
(L–Todeschi–Vialard '24)
Examples
Gromov–Wasserstein
Costs on measures. The following are NNCC:
Relative entropy \(\operatorname{KL}(\mu,\nu)=\int \log\Big(\frac{d\mu}{d\nu}\Big)\,d\mu\),
Hellinger \(D(\mu,\nu)=\displaystyle\int\Big(\sqrt{\frac{d\mu}{d\lambda}}-\sqrt{\frac{d\nu}{d\lambda}}\Big)^2\,d\lambda\),
Fisher–Rao = length space associated with Hellinger
\((\mathbb{G}\times\mathbb{G},\operatorname{GW}^2)\) is NCCC
\(\mathbf{X}=[X,f,\mu]\) and \(\mathbf{Y}=[Y,g,\nu]\in\mathbb{G}\)
\operatorname{GW}^2(\mathbf{X},\mathbf{Y})=\inf_{\pi\in\Pi(\mu,\nu)}\int\lvert f(x,x')-g(y,y')\rvert^2\,d\pi(x,y)\,d\pi(x',y')\,.
Any Hilbert or Bregman cost is NNCC:
c(x,y)=u(x)-u(y)-\langle\nabla u(y),x-y\rangle
G. Peyré
Convergence rates for minimizing movements
Suppose that for each \(x\in X\) and \(n\geq 0\),
Then sublinear (\(\mu=0\)) or linear (\(\mu>0\)) convergence rates.
⏵ there exists a variational c-segment \(s\mapsto (x(s),y_n)\) on \((X\times Y,D)\) with \(x(0)=x_n\) and \(x(1)=x\)
⏵ \(s\mapsto E(x(s))-\mu \,D(x(s),y_{n+1})\) is convex
⏵ \(\displaystyle\lim_{s\to 0^+}\frac{D(x(s),y_{n+1})}{s}=0\)
Theorem.
(L–Aubin-Frankowski '23)
x_n \in\operatorname*{argmin}_{x\in X}E(x)+D(x,y_n), \quad y_{n+1} \in\operatorname*{argmin}_{y\in Y} D(x_n,y)
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0)}{n}
E(x_n)\leq E(x)+\frac{C(x,x_0,y_0,\mu)}{(1+\mu)^n-1}
Thank you!
(Lyon 2025-01-29)
By Flavien Léger
