The back-and-forth method for Wasserstein gradient flows
Joint work with Matt Jacobs and Wonjun Lee (UCLA)
Flavien Léger (ENS PSL)
Wasserstein gradient flows
\[\partial_t\rho-\mathrm{div}(\rho\nabla\phi)=0,\]
\[\phi=\delta U(\rho)\]
on a domain \(\Omega\subset\mathbb{R}^2\), with initial condition \(\rho(t=0)=\rho_0\).
Slow diffusion
\[U(\rho)=\int_\Omega \rho(x)^m+V(x)\rho(x)\,dx,\]
\(m > 1\). \(V(x)\) can be \(+\infty\).
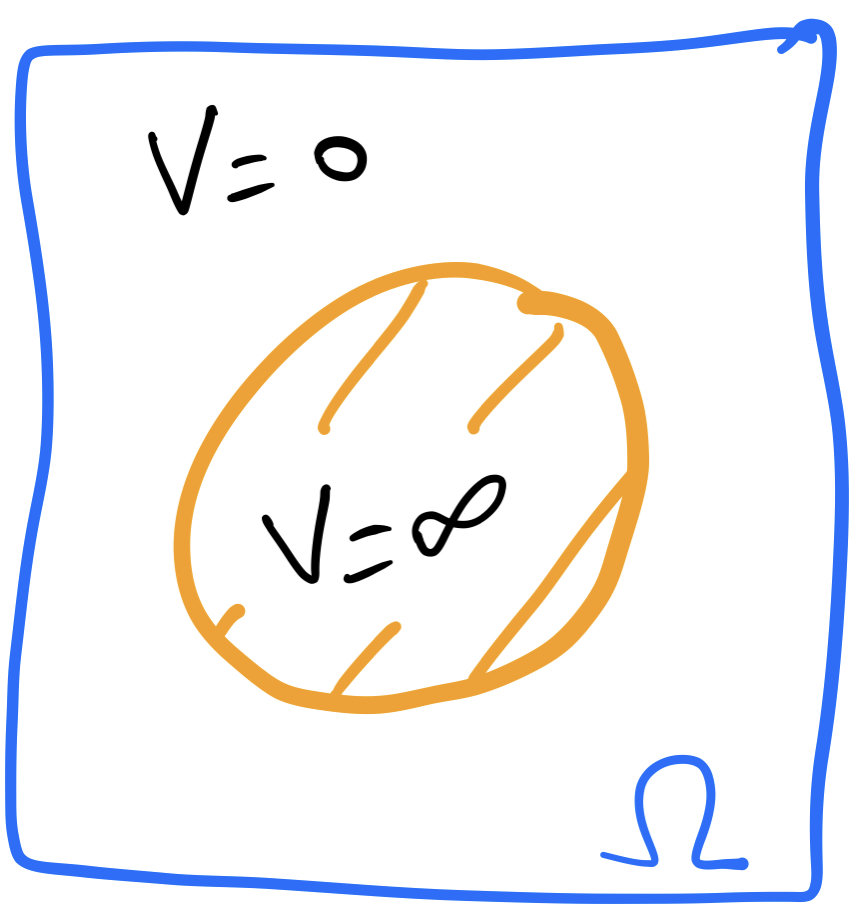
Incompressible energy
\[U(\rho)=\int_\Omega u_\infty(\rho(x))+V(x)\rho(x)\,dx,\]
Aggregation-diffusion
\[U(\rho)=\int_\Omega \rho(x)^m\,dx + \iint_\Omega |x-y|^2\rho(x)\rho(y)\,dxdy\]
u_\infty(\rho)=\begin{cases}
0\quad\text{if } 0\le \rho\le 1\\
+\infty\quad\text{otherwise}
\end{cases}
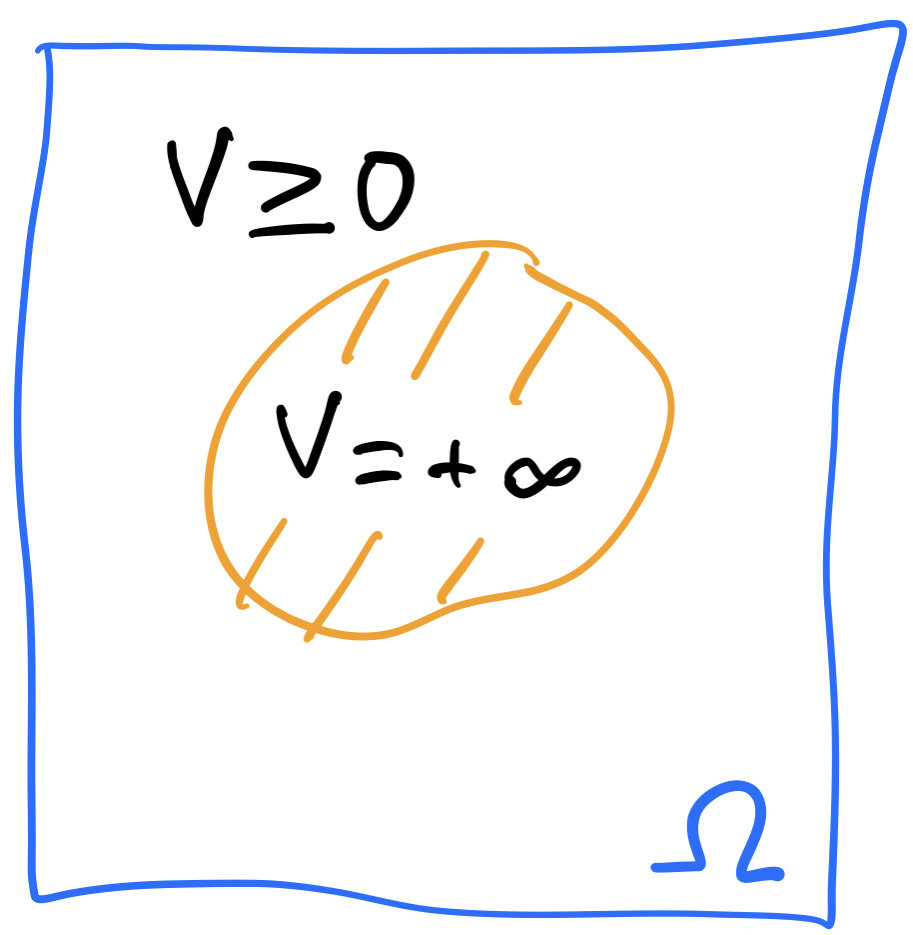
porous medium equation
\(\partial_t\rho=\Delta\rho^m\).
JKO scheme
\[\rho^{(n+1)}=\argmin_\rho U(\rho)+\frac{1}{2\tau}W_2^2(\rho^{(n)},\rho)\]
→ need to solve problems of the form
\[\min_\rho \,U(\rho)+\frac{1}{2\tau}W_2^2(\mu,\rho)\]
for a fixed density \(\mu\).
Dual formulation
Primal:
Example
\(U(\rho)=\iota_{\{\nu\}}(\rho)\) then \(U^*(\phi)=\langle\phi,\nu\rangle\).
\[\sup_{\phi,\psi}\,\langle\psi,\mu\rangle - U^*(\phi)\]
over \((\phi,\psi)\) s.t.
\[\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}.\]
\[\inf_\rho U(\rho)+\frac{1}{2\tau}W_2^2(\mu,\rho).\]
Dual:
Dual formulations
Lemma: \(U^*\) is increasing, i.e.
\[\phi_1\le\phi_2 \implies U^*(\phi_1)\le U^*(\phi_2).\]
\displaystyle\sup_{\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}}\langle\psi,\mu\rangle - U^*(\phi)
Dual formulations
\displaystyle\sup_{\psi(x)-\phi(y)\le\frac{|x-y|^2}{2\tau}}\langle\psi,\mu\rangle - U^*(\phi)
with \(\phi^c(x)=\inf_y\phi(y)+\frac{|x-y|^2}{2\tau}\),
\(\psi^c(y)=\sup_x\psi(x)-\frac{|x-y|^2}{2\tau}\).
☇
\[\sup_\phi\langle\phi^c,\mu\rangle-U^*(\phi)=:J(\phi)\]
\[\sup_\psi\langle\psi,\mu\rangle-U^*(\psi^c)=:I(\psi)\]
Dual formulations
→ unconstrained concave maximization problems
→ Recover \(\rho^*\) from \(\phi^*\) by
\[\rho^*=\delta U^*(\phi^*)\]
\[\sup_\phi\langle\phi^c,\mu\rangle-U^*(\phi)=:J(\phi)\]
\[\sup_\psi\langle\psi,\mu\rangle-U^*(\psi^c)=:I(\psi)\]
The power of duality
\[U(\rho)=\int_\Omega u_\infty(\rho(x))+V(x)\rho(x)\,dx.\]
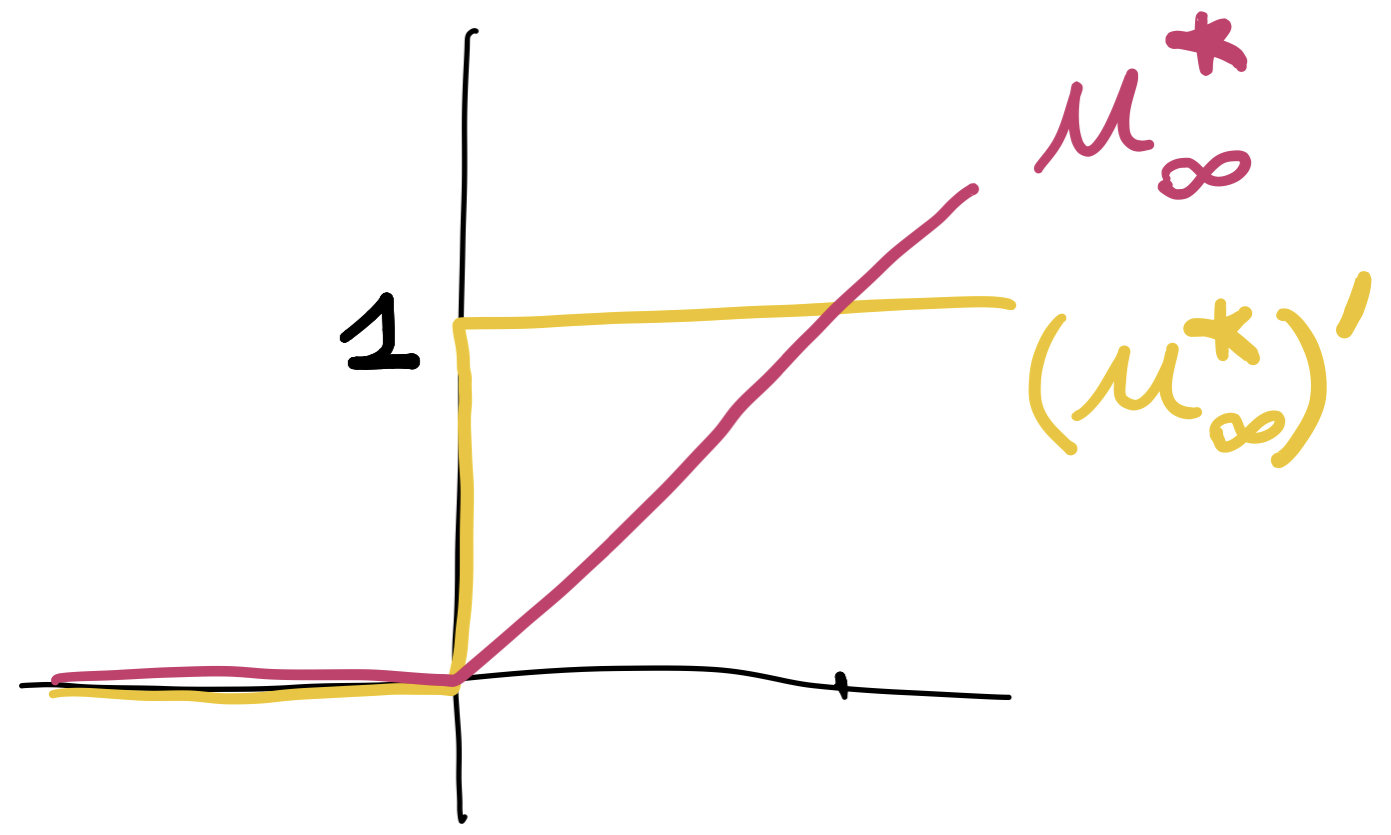
\(\rho(x)=(u^*_\infty)'(\phi(x)-V(x))\) guaranteed to be \(0\) on obstacle.
Remark
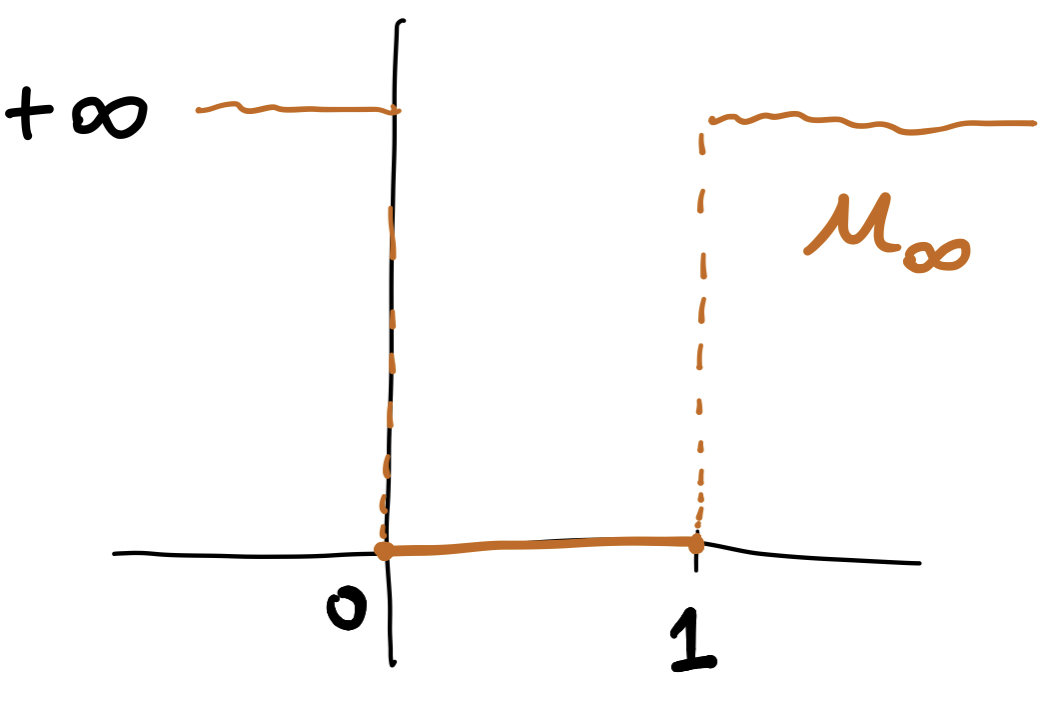
\[U^*(\phi)=\int_\Omega u^*_\infty(\phi(x)-V(x))\,dx\]
☇
Back-and-forth algorithm
\(H\) is the Sobolev space
\[\|h\|_H^2=\int_\Omega\Theta_2|\nabla h(x)|^2+\Theta_1|h(x)|^2\,dx\]
\begin{aligned}
\phi_{k+\frac 1 2}&=\phi_k+\nabla_{\!H}J(\phi_k),\\
\psi_{k+\frac 1 2}&=(\phi_{k+\frac 1 2})^c,\\
\psi_{k+1}&=\psi_{k+\frac 1 2}+\nabla_{\!H}I(\psi_{k+\frac 1 2}),\\
\phi_{k+1} &= (\psi_{k+1})^c
\end{aligned}
\(\nabla_{\!H}J(\phi)=(\Theta_1\mathrm{Id}-\Theta_2\Delta)^{-1}\delta J(\phi)\)
What is \(\nabla_{\!H}J(\phi)\) ?
What is \(\delta J(\phi)\) ?
Recall
\begin{aligned}
J(\phi)&=\langle\phi^c,\mu\rangle-U^*(\phi)\\
&=:F(\phi)-U^*(\phi)
\end{aligned}
Formula: \(\delta F(\phi)=T_{\phi\#}\mu\), where
\[T_\phi(x)=\argmin_y\phi(y)+\frac{|x-y|^2}{2\tau}\]
Why \(H\) ?
Gradient ascent of \(J\) → get Hessian bound
\[0\le -\delta^2\!J(\phi)(h,h)\le \|h\|_H^2\]
\(J=F-U^*\) with \(F(\phi)=\langle\phi^c,\mu\rangle\)
\[-\delta^2\!F(\phi)(h,h)=\tau\int_\Omega\nabla h(x)\cdot\mathrm{cof}(DT_\phi^{-1}(x))\nabla h(x)\,\mu(T_\phi^{-1}(x))dx\]
Why \(H\) ?
\[U^*(\phi)=\int_\Omega u^*_\infty(\phi(x)-V(x))\,dx\]
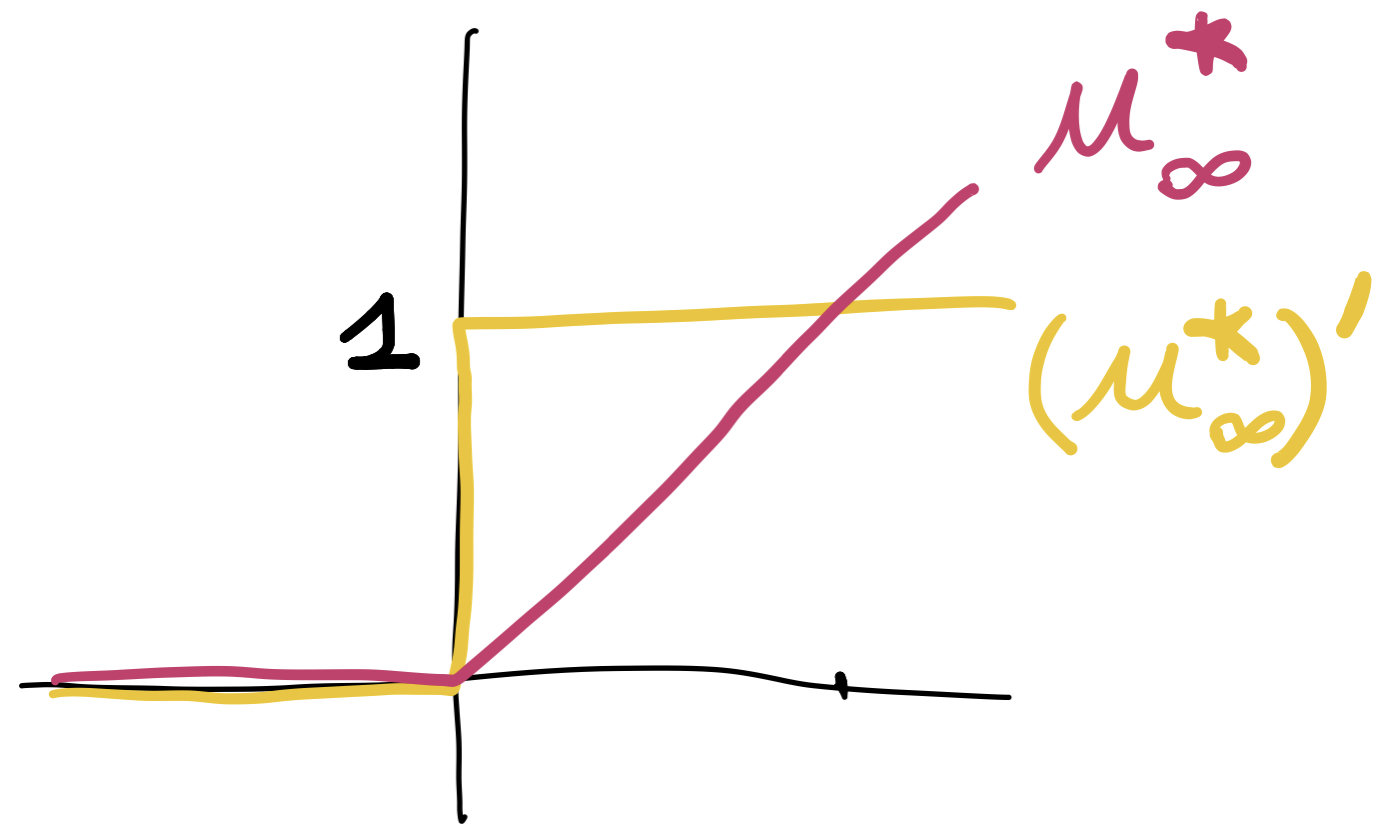
\[\delta^2\!U^*(\phi)(h,h)\le C_\textrm{trace} \int_{\tilde\Omega} |\nabla h(x)|^2+|h(x)|^2\,dx\]
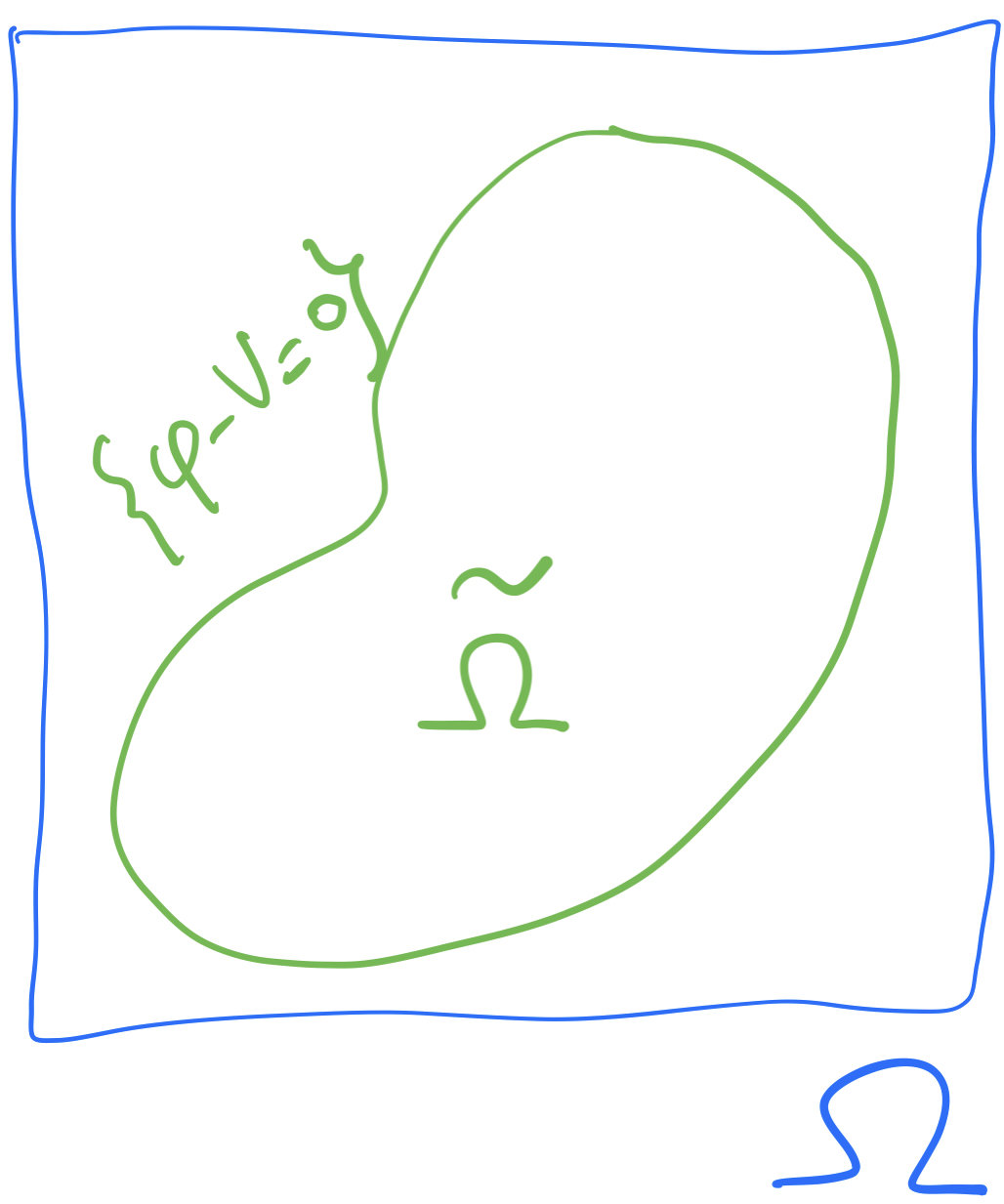
\[\delta^2U^*(\phi)(h,h)=\int_{\{\phi-V=0\}} |h(z)|^2\,d\sigma(z)\]
Movies
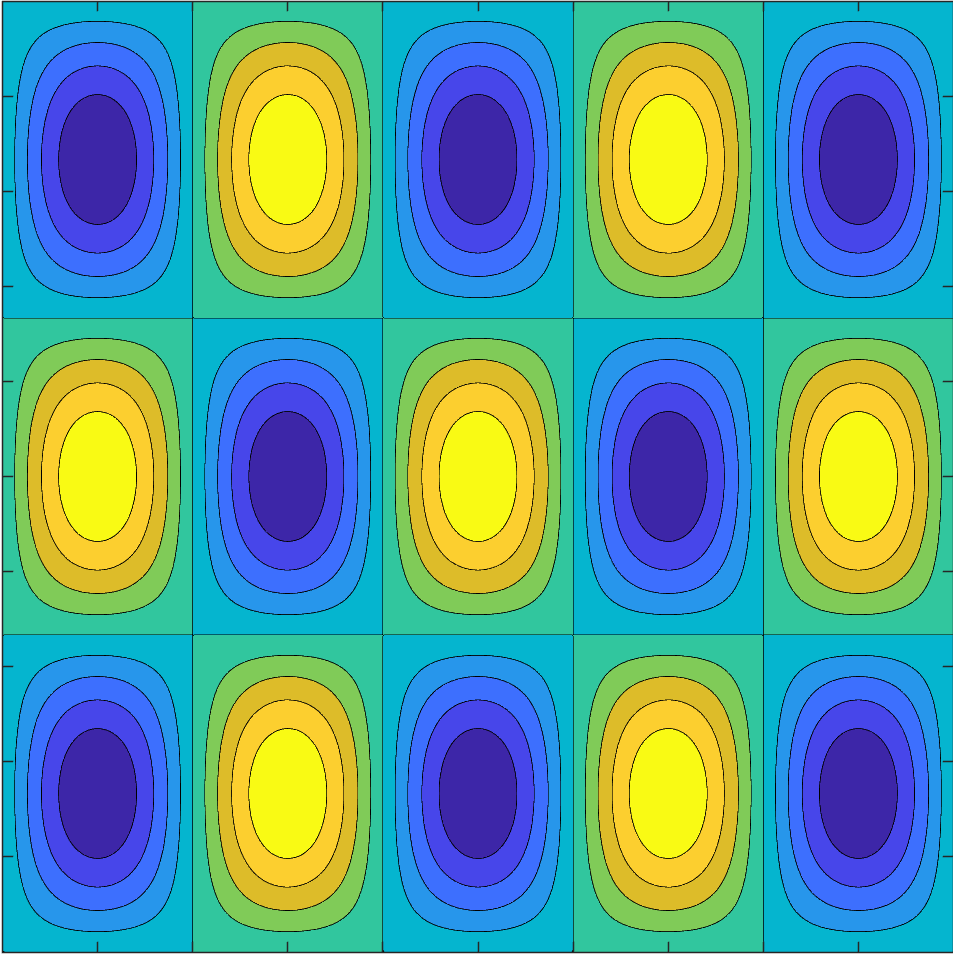
Slow diffusion (porous medium eq)
\(V(x)=-\sin(5\pi x_1)\sin(3\pi x_2)\)
\(512\times 512\) points
\(m=2\)
\(m=4\)
Slow diffusion
\(m=4\)
\(V(x)=\|x-a\|^2\)
\(512\times 512\) points
Incompressible
\(V(x)=\|x-a\|^2\)
\(1024\times 1024\) points
Aggregation-diffusion
\[U(\rho)=\int \rho(x)^3dx+\iint |x-y|^2\rho(x)\rho(y)\,dxdy\]
Thanks!
(mokaplan 2021-01-20) Wasserstein gradient flows
By Flavien Léger
