Математические алгоритмы.
Продолжение

MTUCI ICPC

Ликбез по линейной алгебре

C=AB:C_{ij} = ∑_{i=1}^ k A _{ik}B_{ kj}

Матричное умножение

Умножение матриц. Код

void matmul(const vector<vector<int>>& a,
const vector<vector<int>>& b,
vector<vector<int>>& c){
  for (int i=0;i<a.size();++i){
    for (int j=0;j<b[0].size();++j){
      for (int k=0;k<b.size();++k){
        c[i][j]+=a[i][k]*b[k][j];
      }
    }
  }
  return;
}

Свойства операций над матрицами

Сумма матриц $A$ и $B$ тоже является матрицей: $C_{ij} = A_{ij} + B_{ij}$ .
Сумма матриц коммутативна: $A + B = B + A.$
Сумма матриц ассоциативна: $(A + B) + C = A + (B + C)$ .
Умножение матриц ассоциативно: $(A B) C = A (B C) = A B C$ .
Умножение матриц в общем случае не коммутативно.

Полезные примеры матриц

Равномерное увеличение в n раз:

Перемена координат местами:

Матрица поворота:

Единичная матрица:

n\cdot I

\begin{pmatrix} 0 && 1 \\ 1 && 0 \end{pmatrix}

\begin{pmatrix} \cos (x) && -\sin (x) \\ \sin (x) && \cos (x) \end{pmatrix}

I = \begin{pmatrix} 1 && 0 && 0 \\ 0 && 1 && 0 \\ 0 && 0 && 1 \end{pmatrix} :(A_{ii}=1)

Примеры решения задач с помощью матриц

Вычисление n-ого числа Фиббоначи:

F_n = F_{n-1}+F_{n-2}: \begin{pmatrix} F_{n} \\ F_{n+1} \end{pmatrix} = \begin{pmatrix} 0 && 1\\ 1 && 1 \end{pmatrix} \cdot \begin{pmatrix} F_{n-1} \\ F_{n} \end{pmatrix} \\ \begin{pmatrix} 0*F_{n-1} + 1*F_n \\ 1*F_{n-1} + 1*F_{n}\end{pmatrix} \\ \begin{pmatrix} F_n \\ F_{n+1}\end{pmatrix} = \begin{pmatrix} F_n \\ F_{n-1} + F_{n}\end{pmatrix}

Поиск k-цикла в графе

Рекуррентные формулы в общем виде

Линейные уравнения и метод Гаусса

поменять два уравнения местами,
домножить любое уравнение на ненулевую константу,
вычесть из одного уравнения другое.

Список операций:

Цель:

\begin{pmatrix} x_1 \\ x_2 \\ ... \\ x_n \end{pmatrix} \cdot I = \begin{pmatrix} b_1 \\ b_2 \\ ... \\ b_n \end{pmatrix}

Решение СЛАУ методов Гаусса. Код

void gauss(vector<vector<double>>& a,
vector<double>& b){
  for (int i=0;i<a.size();++i){
    double cc = 1/a[i][i];
    b[i]*=cc;
    for (int j=0;j<a.size();j++){
      a[i][j]*=cc;
    }
    for (int j=0;j<a.size();j++){
        double c2 = a[j][i];
      if (j!=i){
        b[j]-=c2*b[i];
        for (int k=0;k<a.size();++k){
          a[j][k]-=c2*a[i][k];
        }
      }
    }
  }
  return;
}

Интерполяция.
Интерполяционный многочлен Лагранжа

Суть интерполяции

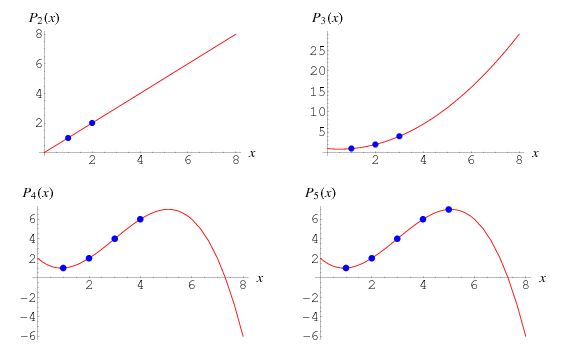
Как считать:

y(x)= \sum_{i=0}^{n} y_i\cdot \prod_{i \ne j} \cfrac{x-x_j}{x_i-x_j}

Задача интерполяции как СЛАУ

aX=y

X = \begin{pmatrix} 1 && x_0 && x_0^2 && ... && x_0^n \\ 1 && x_1 && x_1^2 && ... && x_1^n \\ ... && ... && ... && ... && ... \\ 1 && x_n && x_n^2 && ... && x_n^n \end{pmatrix}

Длинная арифметика и многочлены

Как хранить?

vector<int> digits a; //разряды нашего числа
int base = 10; // может быть любой
// 123459 = {9,5,4,3,2,1}

1 000 000 000 000 = [1000][0]_1e9

Как складывать? По разрядам, а потом

const int base = 10;

vector<int> normalize(vector<int> a) {
    int carry = 0;
    for (int &x : a) {
        x += carry;
        carry = x / base;
        x %= base;
    }
    while (carry > 0) {
        a.push_back(carry % base);
        carry /= base;
    }
    return a;
}

Ускоряем умножение

Алгоритм Карацубы:

A(x) =a_0 +a_1 ⋅x+a_2 ⋅x ^2 +⋯+a_n ⋅x ^n \\ n=2k

a(x)=a_1(x)+x^ka_2(x) \\ b(x)=b_1(x)+x^kb_2(x)

p_1(x)=a_1(x)⋅b_1(x) \\ p_2(x)=a_2(x)⋅b_2(x) \\ t(x)=(a_1(x)+a_2(x))⋅(b_1(x)+b_2(x)) \\ \\ c(x)=a(x)⋅b(x)=p_1(x)+x^k⋅(t(x)−p_1(x)−p_2(x))+x^{2k}\cdot p_2(x)

Алгоритм Карацубы. Код

Кольцо вычетов по модулю

Кольца вычетов по модулю

Расширенный алгоритм Евклида

ax+by=gcd(a,b)

b⋅x'+(a\ mod\ b)⋅y'=g\\ =\\ b⋅x' +(a−⌊\cfrac{b}{a}⌋⋅b)⋅y'=g

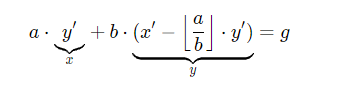
Расширенный алгоритм Евклида. Код

Поиск обратного по модулю

С помощью алгоритма Евклида:

a^{−1}⋅a+k⋅m=1 (mod\ m)

Малая теорема Ферма (для простого модуля)

a^p≡a(mod\ p) \implies a^{p-2} = a^{-1} (mod\ p)

Теорема Эйлера (для любого модуля)

a^{\phi(m)} \equiv 1 \pmod m

Диофантовы уравнения

ax+by=c

Общий вид уравнения:

Еще раз взглянем на расширенный алгоритм Евклида:

ax+by=gcd(a,b)

x,y = (x',y')\cdot \frac{c}{gcd(a,b)}

Решение:

Факторизация чисел

Стандартный алгоритм за sqrt(n)
ро-Алгоритм Полларда O(n^(1/4)logn)
Алгоритм Ферма
...

Ро-алгоритм Полларда

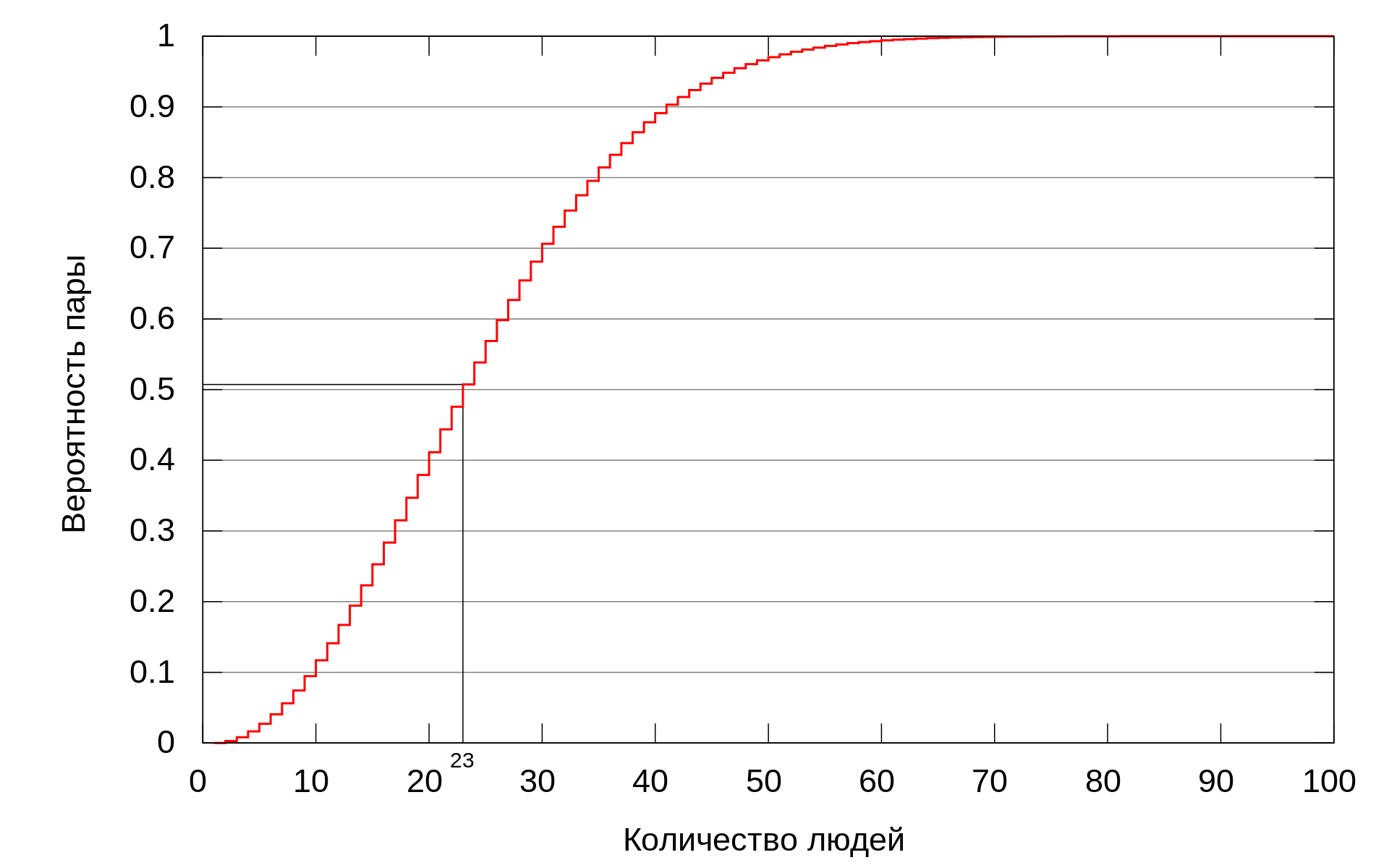
База алгоритма - парадокс дня рождения

Наша "случайная" функция:

f(x) = (x+1)^1 mod\ m

Ро-Алгоритм Полларда

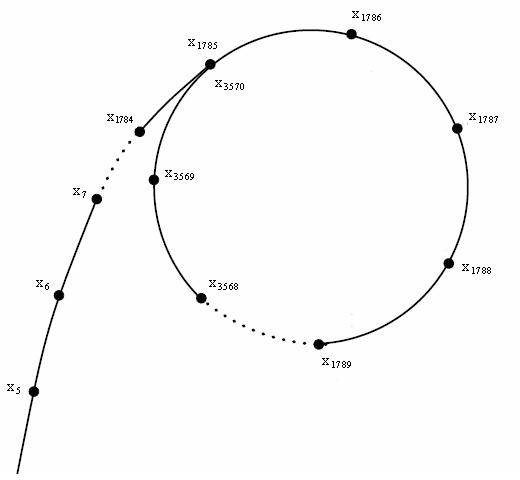
Буква Ро на функциональном графе

p\ -\ \text{наибольший делитель n};p\le\sqrt n\\ f_i(x_0)≡f_ j(x_0)(mod\ p)\\ d=gcd(∣f_i(x_0)−f_j(x_0)∣,n) \\ gcd(∣f_i(x_0)−f_j(x_0)∣,n)\notin\{1,n\}

Ро-алгоритм Полларда. Код

define long long ll;

inline ll f(ll x, ll n) { return (__int128_t) (x + 1) * (x + 1) % n; }

ll find_divisor(ll n, ll seed = 1) {
    ll x = seed, y = seed;
    ll d = 1;
    while (d == 1 || d == n) {
        // двигаем первый указатель на шаг
        y = f(y);
        // а второй -- на два
        x = f(f(x));
        // пытаемся найти общий делитель
        d = gcd(abs(x - y), n);
    }
    return d;
}

Применение факторизации

Взлом шифров (RSA)
Быстрый подсчет функции Эйлера

\phi(x) = \prod_{i=1}^{k}p_i^{a_i-1}(p_i-1)

Комбинаторика

\text{Перестановки без повторений):}\\ P_n=n!\\ \text{Перестановки с повторением}\\ P_n(n_1,n_2,...,n_k) = \cfrac{n!}{n_1! * n_2! * ... * n_k!}\\ \text{Сочетание без повторений: (Не важен порядок)}\\ C_n^k=\cfrac{n!}{k!(n-k)!}=\cfrac{A_n^k}{P_n}\\ C_n^k=C^{n-k}_n\\ \text{Сочетание с повторениями (порядок не важен)}\\ \overline{C_n^k}=C^k_{n+k-1}\\

\text{Мультиномиальные коэффициенты} \\ \text{(Распределение по "ящикам" размера ki)}\\ C_{k_1,k_2,...,k_m}^{n}=\cfrac{n!}{k_1!k_2!...k_m!}\\ \\ \text{Размещение без повторений: (Важен порядок)}\\ A_n^k=n*(n-1)...(n-k+1)=\cfrac{n!}{(n-k)!}\\ \\ \text{Размещение с повторениями (порядок важен)}\\ \overline{A_n^k}=n^k\\ \\ \text{Числа Каталана}\\ C_n = \cfrac{1}{n+1}C_{2n}^{n}

Вероятность

P(A)=\cfrac{N(A)}{N(\Omega)}=\cfrac{|A|}{|\Omega|}=\cfrac{m}{n}\\ 0\le P(A) \le 1\\ P(\empty)=0\\ P(\Omega)=1\\ \text{Если величины несовместные:}\\ P(A+B)=P(A)+P(B)\\ A*B=\empty\\ P(A)+P(\overline{A})=1\\ P(A)=1-P(\overline{A})\\

\text{Мат. Ожидание}\\ E[x]=\sum_ip_ix_i

Марковские цепи

\begin{pmatrix}0 && 1/2 && 1/3 \\1 && 0 && 1/3 \\ 0 && 1/2 && 1/3\end{pmatrix} - \text{Матрица перехода}

Вы устроились на работу в крупную IT компанию, но, придя в офис, обнаружили, что лифт едет на случайные этажи с определенными вероятностями перехода. Как узнать распределение вероятности этажа, на котором вы окажетесь после k-поездок на этом лифте?

\begin{pmatrix}0 && 1/2 && 1/3 \\1 && 0 && 1/3 \\ 0 && 1/2 && 1/3\end{pmatrix} \cdot \begin{pmatrix} 1\\0\\0\end{pmatrix} = \begin{pmatrix} 0\\1\\0\end{pmatrix} - \text{состояние после первого шага} \\

\begin{pmatrix}0 && 1/2 && 1/3 \\1 && 0 && 1/3 \\ 0 && 1/2 && 1/3\end{pmatrix}^n \cdot \begin{pmatrix} 1\\0\\0\end{pmatrix} - \text{состояние после n шагов}

Быстрое вычисление факториала по модулю

\text{Общая часть блоков:} (p-1)!mod\ p=p-1

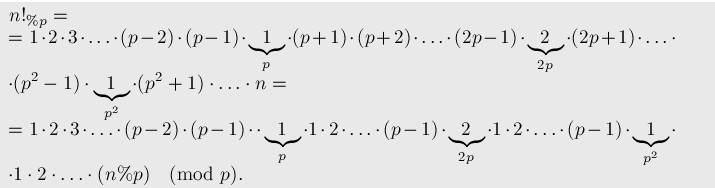
Быстрое вычисление факториала по модулю. Код

int calc(int n, int p){
    int res=1;
    int t=1;
    while(n>1){
        if (n/p%2){
            t = p - 1;
        }
        else{
            t = 1
        };
        res = res * t % p;
        for (int i=2;i<=n%p;++i){
            res = res * i % p;
        }
        n/=p;
    }
    return res % p;
}

Математические алгоритмы.
Продолжение

Ликбез по линейной алгебре

Умножение матриц. Код

Свойства операций над матрицами

Полезные примеры матриц

Примеры решения задач с помощью матриц

Линейные уравнения и метод Гаусса

Решение СЛАУ методов Гаусса. Код

Интерполяция.
Интерполяционный многочлен Лагранжа

Задача интерполяции как СЛАУ

Длинная арифметика и многочлены

Ускоряем умножение

Алгоритм Карацубы. Код

Кольцо вычетов по модулю

Кольца вычетов по модулю

Расширенный алгоритм Евклида. Код

Поиск обратного по модулю

Диофантовы уравнения

Факторизация чисел

Ро-алгоритм Полларда

Ро-Алгоритм Полларда

Ро-алгоритм Полларда. Код

Применение факторизации

Комбинаторика

Вероятность

Марковские цепи

Быстрое вычисление факториала по модулю

Быстрое вычисление факториала по модулю. Код

Полезные формулы и фишки

Advanced Math Algorithms

Advanced Math Algorithms

Fleming Kris

Математические алгоритмы. Продолжение

Ликбез по линейной алгебре

Умножение матриц. Код

Свойства операций над матрицами

Полезные примеры матриц

Примеры решения задач с помощью матриц

Линейные уравнения и метод Гаусса

Решение СЛАУ методов Гаусса. Код

Интерполяция. Интерполяционный многочлен Лагранжа

Задача интерполяции как СЛАУ

Длинная арифметика и многочлены

Ускоряем умножение

Алгоритм Карацубы. Код

Кольцо вычетов по модулю

Кольца вычетов по модулю

Расширенный алгоритм Евклида. Код

Поиск обратного по модулю

Диофантовы уравнения

Факторизация чисел

Ро-алгоритм Полларда

Ро-Алгоритм Полларда

Ро-алгоритм Полларда. Код

Применение факторизации

Комбинаторика

Вероятность

Марковские цепи

Быстрое вычисление факториала по модулю

Быстрое вычисление факториала по модулю. Код

Полезные формулы и фишки

Advanced Math Algorithms

More from Fleming Kris

Математические алгоритмы.
Продолжение

Интерполяция.
Интерполяционный многочлен Лагранжа