Графы. Алгоритмы на графах
MTUCI ICPC
Graph be like:
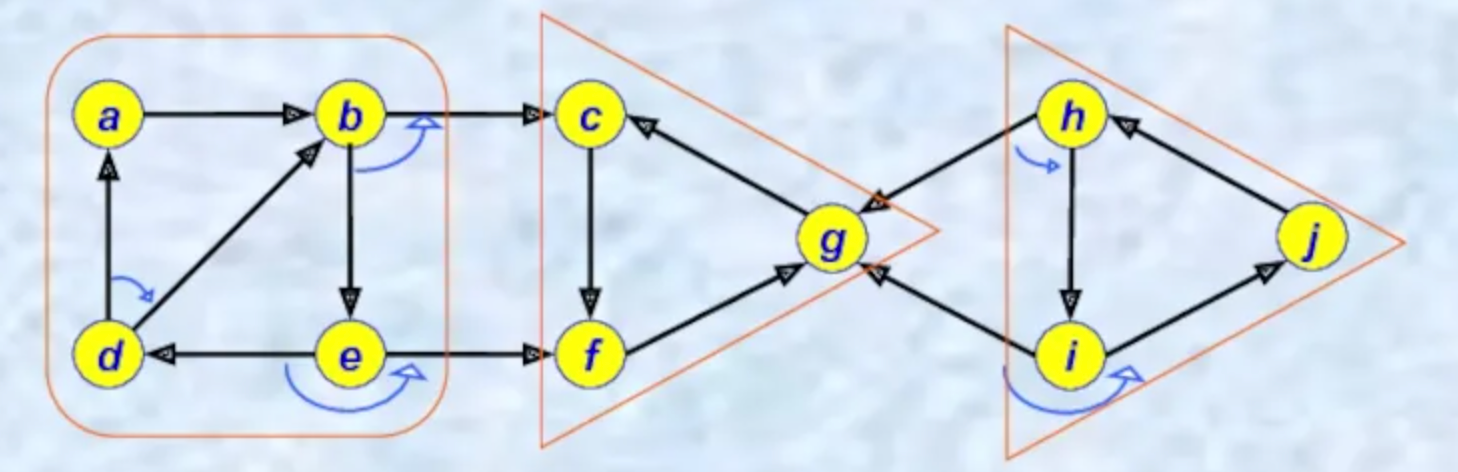
Oriented graph be like
Хранение графов в памяти. Невзвешенный граф
int main() {
int n_vertices,n_edges;
cin>>n_vertices>>n_edges;
vector<vector<int>> graph1(n_vertices,vector<int>(n_vertices));
vector<vector<int>> graph2(n_vertices);
vector<pair<int,int>> graph3;
int a,b;
for (int i=0;i<n_edges;++i){
cin>>a>>b;
graph1[a][b]=1;
graph2[a].push_back(b);
graph3.emplace_back(a,b);
}
}# PRESENTING CODE
Взвешенный случай
struct Edge{
int a;
int b;
int w;
};
int main() {
int n_vertices,n_edges;
cin>>n_vertices>>n_edges;
vector<vector<int>> graph1(n_vertices,vector<int>(n_vertices)); //матрица смежности
vector<vector<pair<int,int>>> graph2(n_vertices); //списки смежности
vector<Edge> graph3; //список ребер
int a,b,w;
for (int i=0;i<n_edges;++i){
cin>>a>>b>>w;
graph1[a][b]=w;
graph2[a].emplace_back(b,w);
graph3.push_back(Edge{a,b,w});
}
}# PRESENTING CODE
Поиск в глубину и его применения:
- Поиск любого пути в графе.
- Поиск лексикографически первого пути в графе.
- Проверка, является ли одна вершина дерева предком другой
- Задача LCA (наименьший общий предок).
- Топологическая сортировка:
- Проверка графа на ацикличность и нахождение цикла
- Поиск компонент сильной связности
- Поиск мостов
Поиск в глубину(DFS)
void DFS(const vector<vector<pair<int,int>>>& graph, vector<bool>& visited, int vertex){
visited[vertex]=true;
for (auto v:graph[vertex]){
int new_vert=v.first;
if(!visited[new_vert]){
DFS(graph,visited,new_vert);}
}
}
# PRESENTING CODE
Поиск компонент связностей

Решение задачи подсчета компонент связности
#include <iostream>
#include "algorithm"
#include "vector"
using namespace std;
void DFS(const vector<vector<pair<int,int>>>& graph, vector<bool>& visited, int vert){
visited[vert]=true;
for (auto a:graph[vert]){
int node=a.first;
if(!visited[node]){
DFS(graph, visited, node);
}
}
}
int main() {
int n_vertices,n_edges;
cin>>n_vertices>>n_edges;
vector<vector<pair<int,int>>> graph2(n_vertices); //списки смежности
int a,b,w;
for (int i=0;i<n_edges;++i){
cin>>a>>b;
graph2[a-1].emplace_back(b-1,1);
graph2[b-1].emplace_back(a-1,1);
}
vector<bool> visited(n_vertices,false);
int count=1;
DFS(graph2, visited,0);
for (int i=1;i<n_vertices;++i){
if(!visited[i]){
count++;
DFS(graph2, visited, i);
}
}
cout<<'\n'<<count;
}# PRESENTING CODE
Проверка графа на двудольность

Код для проверки на двудольность
enum color {
RED, BLUE, GRAY
};
color invert_colors(color a) {
if (a == RED) {
return BLUE;
}
return RED;
}
bool DFS(const vector<vector<int>> &graph, vector<color> &visited, int vert, color pred) {
visited[vert] = pred;
bool f=true;
for (auto node: graph[vert]) {
if (visited[node] == GRAY) {
f&=DFS(graph, visited, node, invert_colors(visited[vert]));
}
else if (visited[node] == visited[vert]) {
return false;
}
}
return f;
}
int main() {
int n_vertices, n_edges;
cin >> n_vertices >> n_edges;
vector<vector<pair<int, int>>> graph2(n_vertices); //списки смежности
int a, b, w;
for (int i = 0; i < n_edges; ++i) {
cin >> a >> b;
graph2[a - 1].emplace_back(b - 1, 1);
graph2[b - 1].emplace_back(a - 1, 1);
}
vector<color> visited(n_vertices, GRAY);
cout<<DFS(graph2,visited, 0, RED);
}# PRESENTING CODE
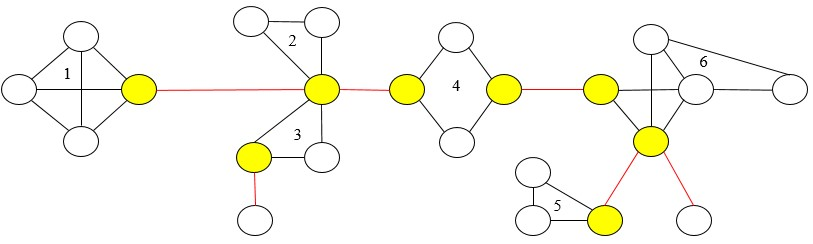
Поиск мостов в графе:

void DFS(const vector<vector<pair<int, int>>> &graph, vector<bool> &visited, int vert, int pt, int pred, vector<int>& tin,vector<int>& tmin) {
int cur_time=pt+1;
tin[vert]=cur_time;
tmin[vert]=cur_time;
visited[vert] = true;
for (auto a: graph[vert]) {
int node = a.first;
if(node==pred){
continue;
}
if (!visited[node]) {
DFS(graph, visited, node,cur_time,vert,tin,tmin);
tmin[vert]=min(tmin[vert], tmin[node]);
if(tmin[vert]<tmin[node]){
cout<<vert+1<<' '<<node+1<<'\n';
}
}
else{
tmin[vert]=min(tmin[vert], tmin[node]);
}
}
}
int main() {
int n_vertices, n_edges;
cin >> n_vertices >> n_edges;
vector<vector<pair<int, int>>> graph2(n_vertices); //списки смежности
int a, b, w;
for (int i = 0; i < n_edges; ++i) {
cin >> a >> b;
graph2[a - 1].emplace_back(b - 1, 1);
graph2[b - 1].emplace_back(a - 1, 1);
}
vector<int> time_in(n_vertices,1e7);
vector<int> time_min(n_vertices,1e7);
vector<bool> visited(n_vertices, false);
DFS(graph2,visited, 0, -1,-1,time_in,time_min);
}# PRESENTING CODE
Код решения
Поиск цикла в графе
const int INF = 1e9;
using namespace std;
void DFS(const vector<vector<pair<int,int>>>& graph, vector<int>& visited, int vertex, int time_pred){
visited[vertex]=time_pred+1;
for (auto v:graph[vertex]){
int node =v.first;
if(visited[node]<visited[vertex]){
cout<<"Hello, I'm cycled";
return;
}
if(visited[node]==INF){
DFS(graph, visited, node, visited[vertex]);
}
}
}
int main() {
int n_vertices, n_edges;
cin >> n_vertices >> n_edges;
vector<vector<pair<int, int>>> graph2(n_vertices); //списки смежности
int a, b, w;
for (int i = 0; i < n_edges; ++i) {
cin >> a >> b;
graph2[a - 1].emplace_back(b - 1, 1);
}
vector<int> visited(n_vertices, INF);
DFS(graph2, visited, 0, -1);
}# PRESENTING CODE
Решение для поиска цикла
Топологическая сортировка графа
# PRESENTING CODE
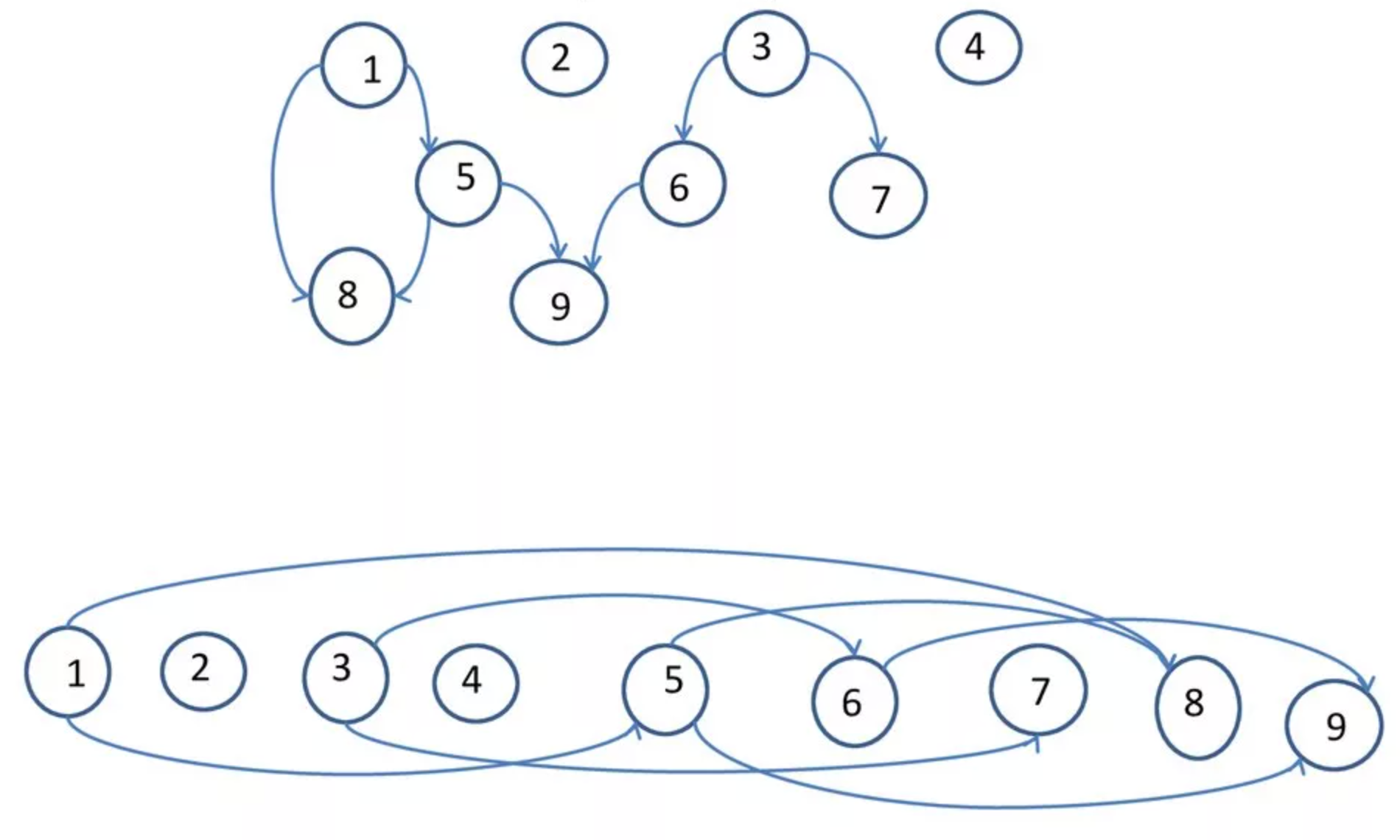
const int INF = 1e9;
using namespace std;
void DFS(const vector<vector<pair<int,int>>>& graph, vector<bool>& visited, int vertex, vector<int>& ans){
visited[vertex]=true;
for (auto v:graph[vertex]){
int node =v.first;
if(!visited[node]){
DFS(graph, visited, node, ans);
}
}
ans.push_back(vertex);
}
int main() {
int n_vertices, n_edges;
cin >> n_vertices >> n_edges;
vector<vector<pair<int, int>>> graph2(n_vertices); //списки смежности
int a, b, w;
for (int i = 0; i < n_edges; ++i) {
cin >> a >> b;
graph2[a - 1].emplace_back(b - 1, 1);
}
vector<bool> visited(n_vertices, false);
vector<int> ans;
DFS(graph2, visited, 0,ans);
for (auto i=ans.rbegin();i<ans.rend();i++){
cout<<*i<<'\n';
}
}# PRESENTING CODE
Решение
Поиск компонент сильной связности
#include "iostream"
#include "vector"
void TopSort(const std::vector<std::vector<int>>& graph, std::vector<bool>& visited, int vertex, std::vector<int>& order){
visited[vertex]=true;
for (int node: graph[vertex]){
if(!visited[node]){
TopSort(graph,visited, node, order);
}
}
order.push_back(vertex);
}
void DFS(const std::vector<std::vector<int>>& graph, std::vector<bool>& visited, int vertex, std::vector<int>& component, int n_comp){
component[vertex]=n_comp;
for (int node: graph[vertex]){
if(component[node]==0){
DFS(graph, visited, node, component, n_comp);
}
}
}
int main(){
size_t n_vertices, n_edges;
std::cin>>n_vertices>>n_edges;
std::vector<std::vector<int>> graphIshod(n_vertices, std::vector<int>());
std::vector<std::vector<int>> graphT(n_vertices, std::vector<int>());
int a,b;
for(size_t i=0;i<n_edges;++i){
std::cin>>a>>b;
graphIshod[a - 1].push_back(b - 1);
graphT[b-1].push_back(a-1);
}
std::vector<bool> visited(n_vertices);
std::vector<int> order;
for (int i=0;i<n_vertices;++i){
if(!visited[i]){
TopSort(graphIshod, visited, i, order);
}
}
std::reverse(order.begin(), order.end());
std::vector<int> component(n_vertices, 0);
int n_comp=1;
for (int i:order){
if(component[i]==0){
DFS(graphT,visited,i,component,n_comp);
n_comp++;
}
}
for(size_t i=0;i<n_vertices;++i){
std::cout<<i<<' '<<component[i]<<'\n';
}
return 0;
}# PRESENTING CODE
Конденсация графа
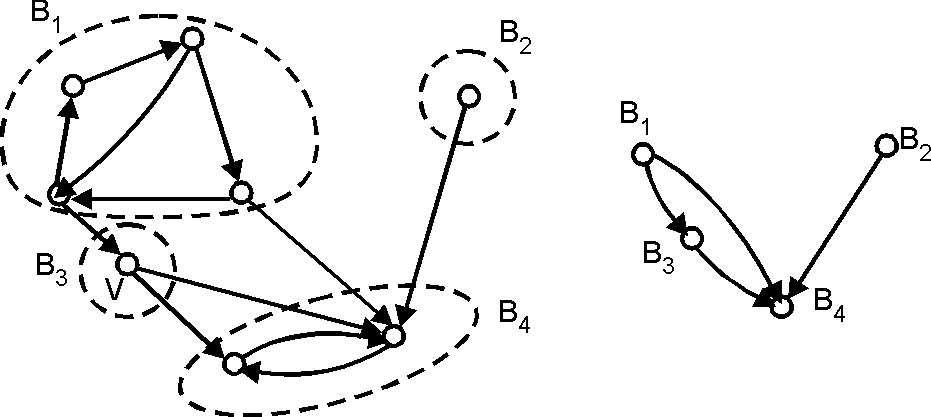
#include "iostream"
#include "vector"
#include "set"
void TopSort(const std::vector<std::vector<int>>& graph, std::vector<bool>& visited, int vertex, std::vector<int>& order){
visited[vertex]=true;
for (int node: graph[vertex]){
if(!visited[node]){
TopSort(graph,visited, node, order);
}
}
order.push_back(vertex);
}
void DFS(const std::vector<std::vector<int>>& graph, std::vector<bool>& visited, int vertex, std::vector<int>& component, int n_comp){
component[vertex]=n_comp;
for (int node: graph[vertex]){
if(component[node]==0){
DFS(graph, visited, node, component, n_comp);
}
}
}
int main(){
size_t n_vertices, n_edges;
std::cin>>n_vertices>>n_edges;
std::vector<std::vector<int>> graphIshod(n_vertices, std::vector<int>());
std::vector<std::vector<int>> graphT(n_vertices, std::vector<int>());
int a,b;
for(size_t i=0;i<n_edges;++i){
std::cin>>a>>b;
graphIshod[a - 1].push_back(b - 1);
graphT[b-1].push_back(a-1);
}
std::vector<bool> visited(n_vertices);
std::vector<int> order;
for (int i=0;i<n_vertices;++i){
if(!visited[i]){
TopSort(graphIshod, visited, i, order);
}
}
std::reverse(order.begin(), order.end());
std::vector<int> component(n_vertices, 0);
int n_comp=0;
for (int i:order){
if(component[i]==0){
n_comp++;
DFS(graphT,visited,i,component,n_comp);
}
}
std::vector<std::set<int>> graph_cond(n_comp);
for (size_t i=0;i<n_vertices;++i){
for (int j:graphIshod[i]){
graph_cond[component[i]].insert(component[j]);
}
}
return 0;
}# PRESENTING CODE
Кратчайшие пути
Поиск в ширину(BFS):
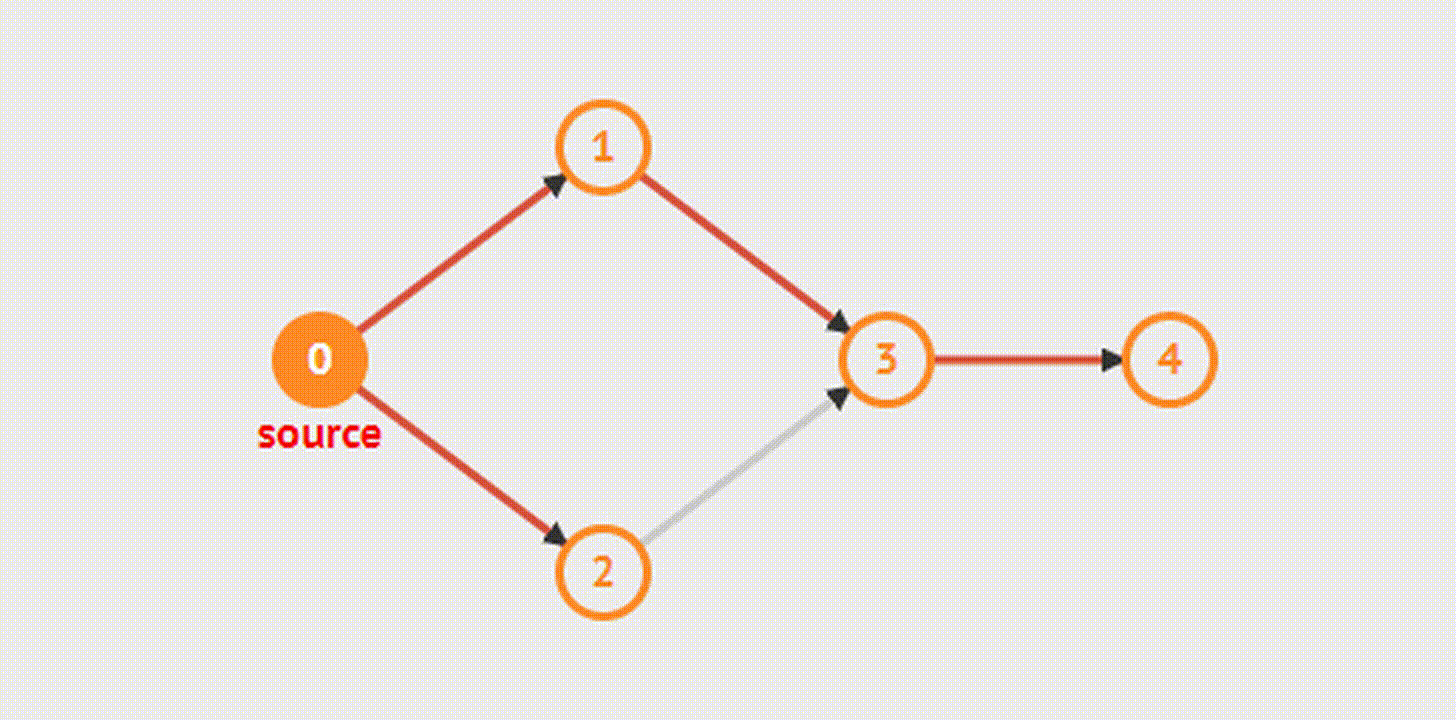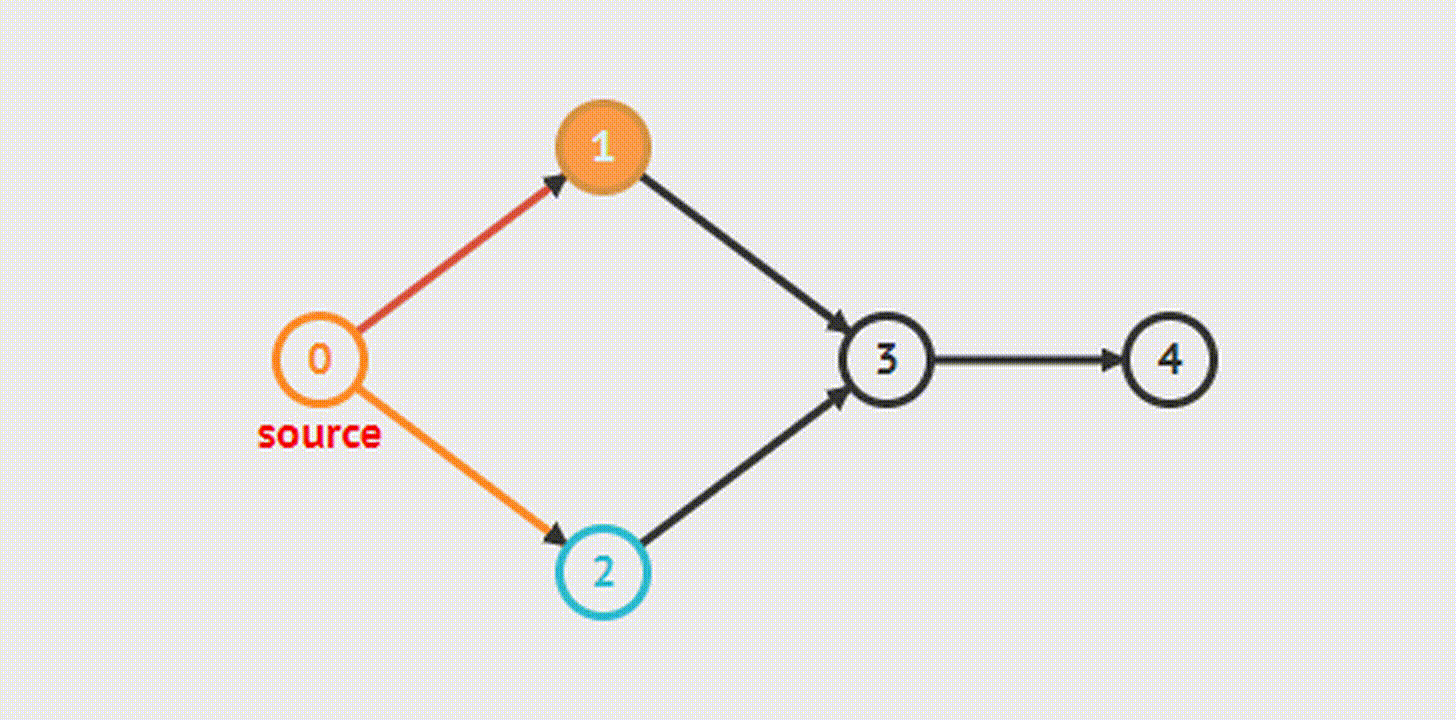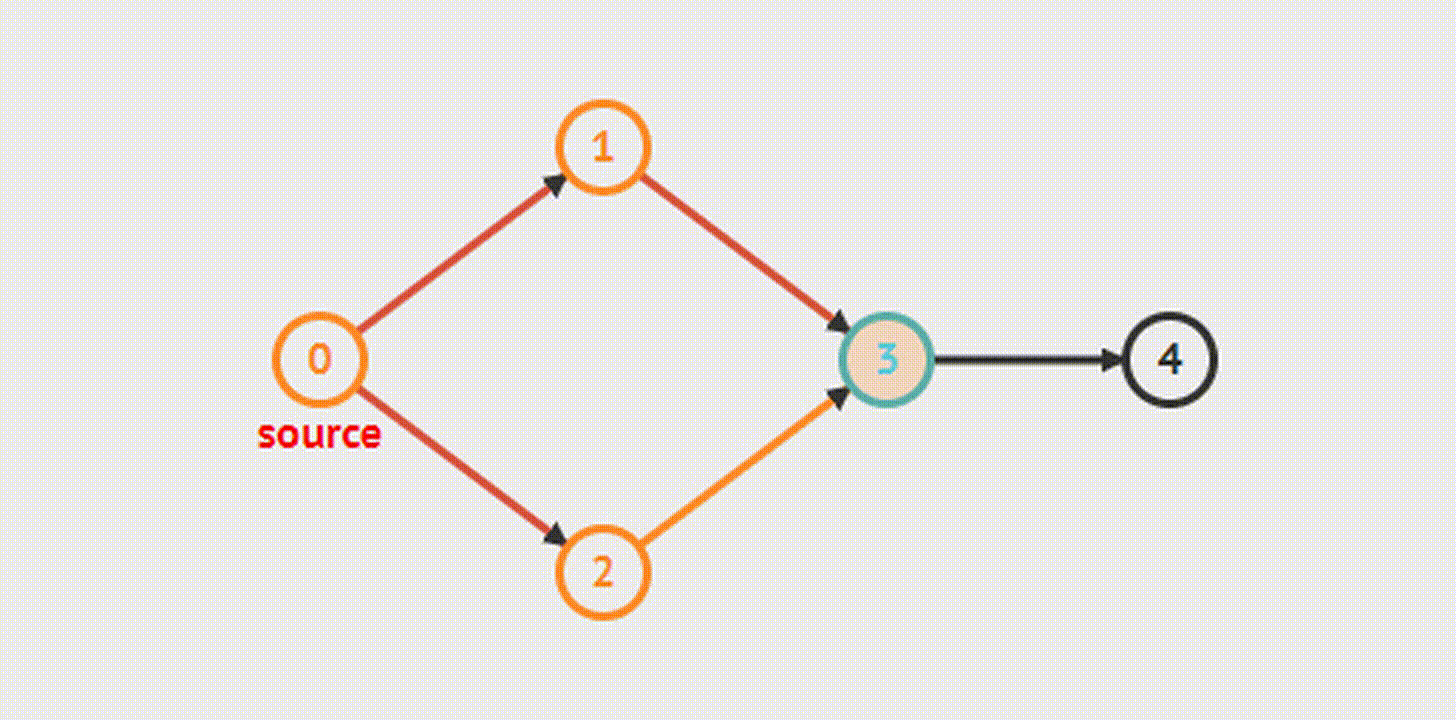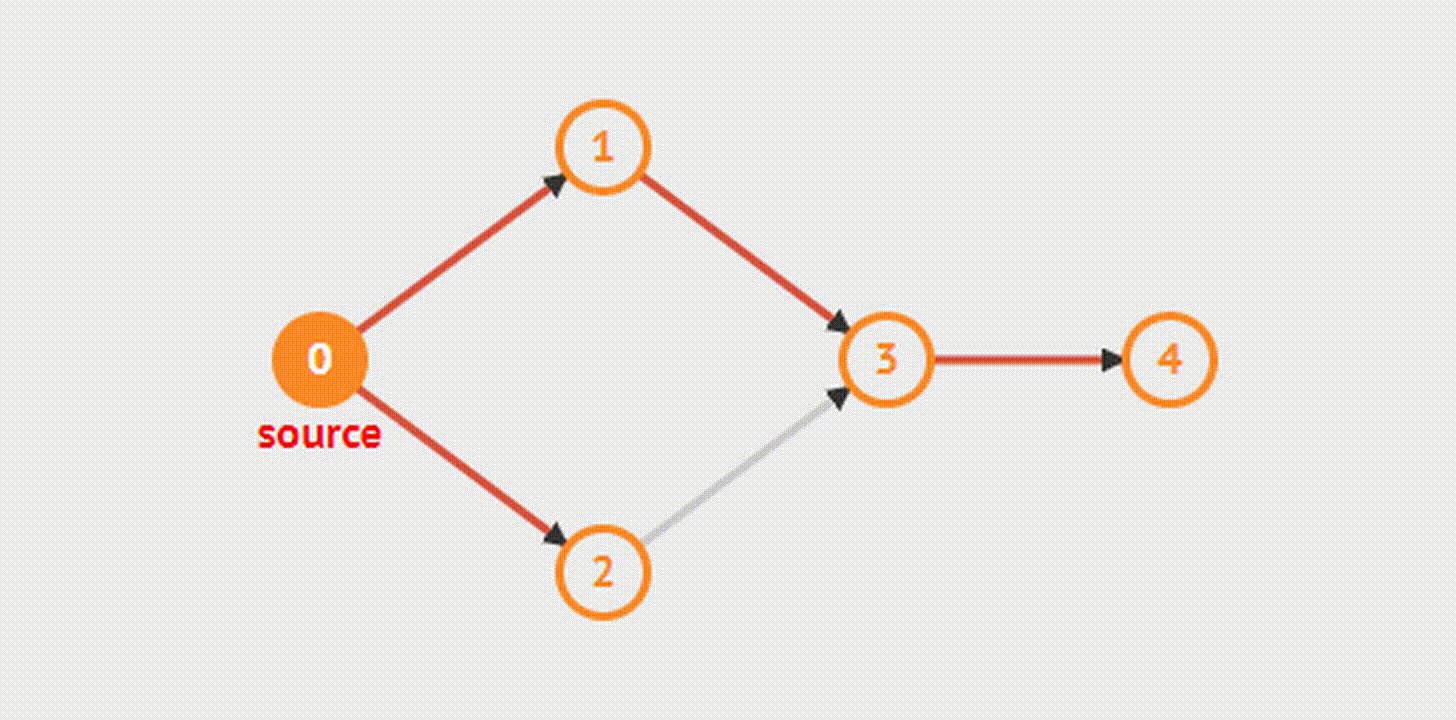
vector<int> g[maxn];
void bfs(int s) {
queue<int> q;
q.push(s);
vector<int> d(n, -1), p(n);
d[s] = 0;
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : g[v]) {
if (d[u] == -1) {
q.push(u);
d[u] = d[v] + 1;
p[u] = v;
}
}
}
} # PRESENTING CODE
Решение
Алгоритм Дейкстры:
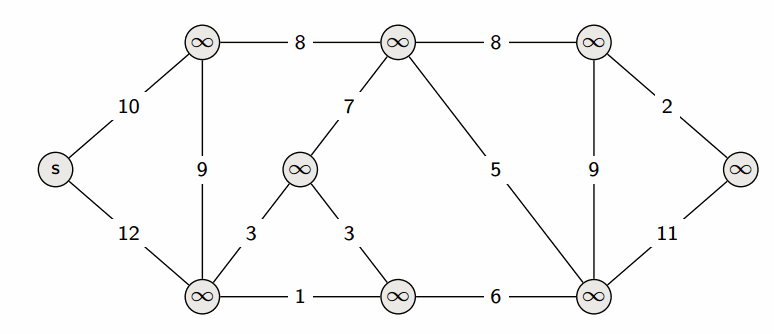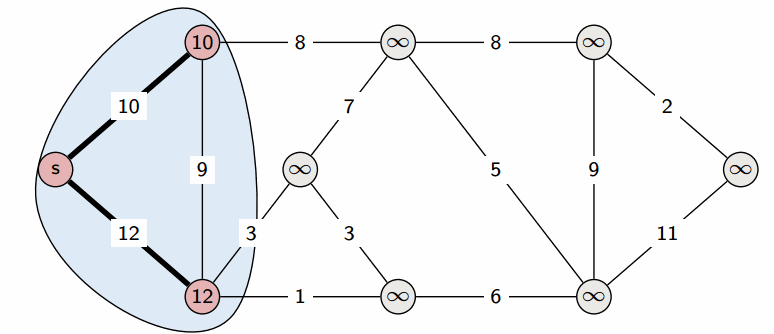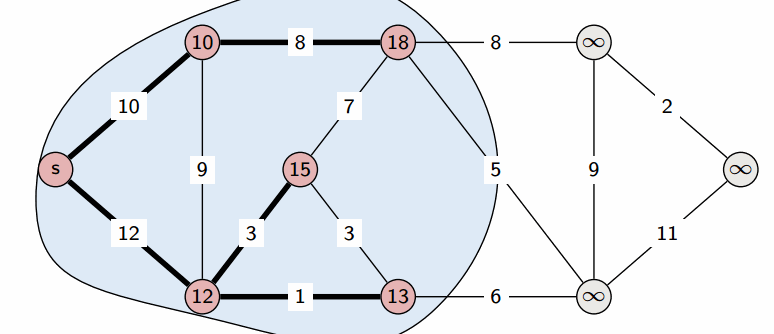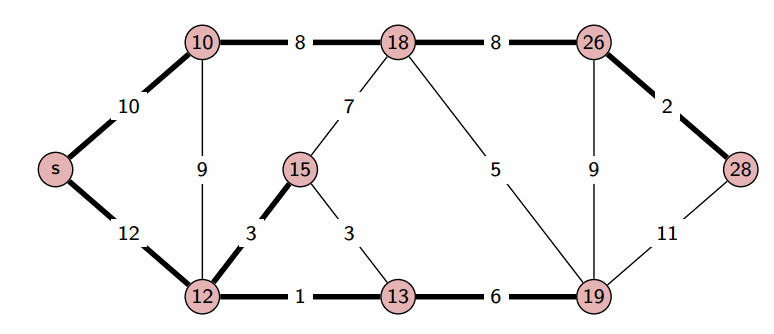
int main() {
int n;
... чтение n ...
vector < vector < pair<int,int> > > g (n);
... чтение графа ...
int s = ...; // стартовая вершина
vector<int> d (n, INF), p (n);
d[s] = 0;
set < pair<int,int> > q;
q.insert (make_pair (d[s], s));
while (!q.empty()) {
int v = q.begin()->second;
q.erase (q.begin());
for (size_t j=0; j<g[v].size(); ++j) {
int to = g[v][j].first,
len = g[v][j].second;
if (d[v] + len < d[to]) {
q.erase (make_pair (d[to], to));
d[to] = d[v] + len;
p[to] = v;
q.insert (make_pair (d[to], to));
}
}
}
}# PRESENTING CODE
Алгоритм Дейкстры
void solve() {
vector<int> d (n, INF);
d[v] = 0;
vector<int> p (n, -1);
int x;
for (int i=0; i<n; ++i) {
x = -1;
for (int j=0; j<m; ++j)
if (d[e[j].a] < INF)
if (d[e[j].b] > d[e[j].a] + e[j].cost) {
d[e[j].b] = max (-INF, d[e[j].a] + e[j].cost);
p[e[j].b] = e[j].a;
x = e[j].b;
}
}
if (x == -1)
cout << "No negative cycle from " << v;
else {
int y = x;
for (int i=0; i<n; ++i)
y = p[y];
vector<int> path;
for (int cur=y; ; cur=p[cur]) {
path.push_back (cur);
if (cur == y && path.size() > 1) break;
}
reverse (path.begin(), path.end());
cout << "Negative cycle: ";
for (size_t i=0; i<path.size(); ++i)
cout << path[i] << ' ';
}
}# PRESENTING CODE
Алгоритм Форда-Беллмана
for (int k=0; k<n; ++k)
for (int i=0; i<n; ++i)
for (int j=0; j<n; ++j)
if (d[i][k] < INF && d[k][j] < INF)
d[i][j] = min (d[i][j], d[i][k] + d[k][j]);# PRESENTING CODE
Алгоритм Флойда-Уоршелла
Остовные деревья
// This slide uses Auto-Animate to animate between
// two different code blocks
const distanceBetween = ( p1, p2 ) => {
// TODO
}
distanceBetween([10,10], [50,50])# PRESENTING CODE
Code Transitions
// This slide uses Auto-Animate to animate between
// two different code blocks
const distanceBetween = ( p1, p2 ) => {
// TODO
}
distanceBetween([10,10], [50,50])# PRESENTING CODE
Code Transitions
// This slide uses Auto-Animate to animate between
// two different code blocks
const distanceBetween = ( p1, p2 ) => {
// TODO
}
distanceBetween([10,10], [50,50])# PRESENTING CODE
Code Transitions
Code
By Fleming Kris
Code
- 321



