Linear Algebra
https://slides.com/georgelee/ics141-matrices/live
What is a matrix?
<Insert Keanu Reeves photo here>
Matrix
A rectangular array of values where every element belongs to a set S. A matrix has m rows and n columns. The element aij belongs to row i and column j.
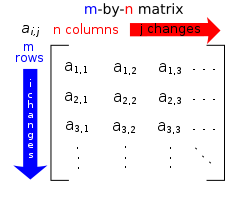
More Matrices
The size of a matrix is m x n. If m = n, we say the matrix is a square matrix.
Matrix Operations
Transposition
The transpose of a matrix A, denoted by At, is the n x m matrix obtained by interchanging the rows and columns.
In other words, if B = At, then aij = bji
[1 2 t = [1 3
3 4] 2 4]
Addition / Subtraction
Provided that two matrices are the same size, we can add or subtract matrices by adding or subtracting their elements.
[ 1 2 + [2 4 = [3 6 3 4 ] 6 8] 9 12]
[1 2 3] + [3 4 5] = [4 6 8]
Multiplying Matrices
- For a row i in A, multiply each element by each element in a column j in B. If we have two matrices of size m x k and
k x n
ABij = Ai,1 * B1,j + Ai,2 * B2,j + Ai,3 * B3,j + ... + Aik + Bkj
Multiplication
Two matrices A and B can be multiplied if the number of columns in the A is the same as the number of rows in the B. Note that matrix multiplication is NOT commutative.
Given two matrices mA x nA and mB x nB, we can multiply them only if nA = mB. The size of the product is mA x nB.
Let's do a 2x2 example
[1 2 x [2 4 = [? ? 3 4] 6 8] ? ?]
[1 2 x [2 4 = [(1*2 + 2*6) ? 3 4] 6 8] ? ?]
[1 2 x [2 4 = [14 (1*4 + 2*8) 3 4] 6 8] ? ?]
Let's do a 2x2 example
[1 2 x [2 4 = [? ? 3 4] 6 8] ? ?]
[1 2 x [2 4 = [14 20 3 4] 6 8] (3*2 + 4*6) ?]
[1 2 x [2 4 = [14 20 3 4] 6 8] 30 (3*4 + 4*8)]
Identity Matrix
The identity matrix of order n is an n x n matrix In = [𝛿ij] where 𝛿ij = 1 if i = j and is 0 otherwise.
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]
Inverse Matrix
The inverse of an n x n matrix A is the the matrix A-1 such that AA-1 = I (the identity matrix).
Symmetric
A matrix A is symmetric if it is equal to its transpose. That is, A = At. For example, the identity matrix is symmetric.
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]
Zero-One Matrices
Zero-One Matrix
A matrix where all the values are either 0 or 1. We can define logic-like operators on it.
The join of zero-one matrices A and B is aij v bij for each element in A and B.
The meet of zero-one matrices A and B is aij ^ bij for each element in A and B.
Boolean Product
Similar to matrix multiplication, we can find a boolean product of two matrices. Instead of multiplication, we have ^, and instead of addition we have v.
That is, if we're multiplying two matrices of size m x k and k x n:
cij = (ai,1 ^ b1,j) v (ai,2 ^ b2,j) v ... v (ai,k ^ bk,j)
Matrices
By George Lee
Matrices
- 1,206



