Kétdimenziós anyagok rezonáns Raman-spektrumának elméleti vizsgálata
Kukucska Gergő
2019. Május 23.
ÚNKP Konferencia
Kukucska Gergő
Tartalom
- Kétdimenziós anyagok
- Raman-spektrumának
- elméleti vizsgálata
Kukucska Gergő
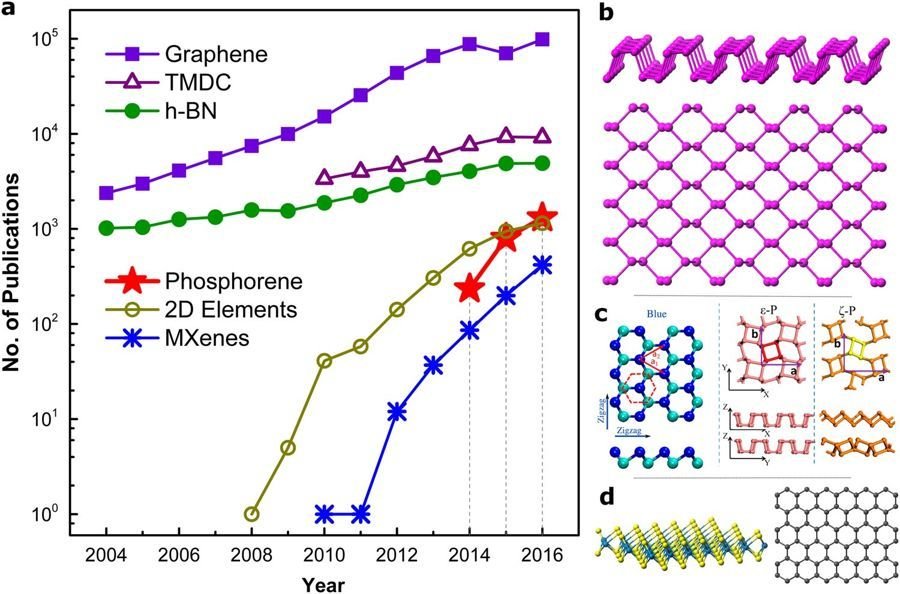
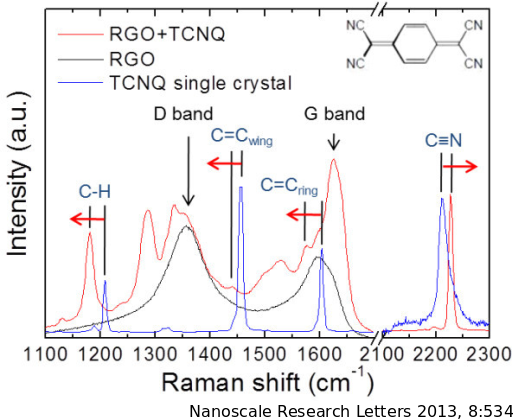
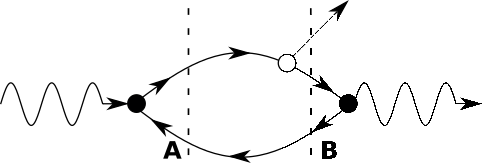
Kétdimenziós anyagok - motiváció
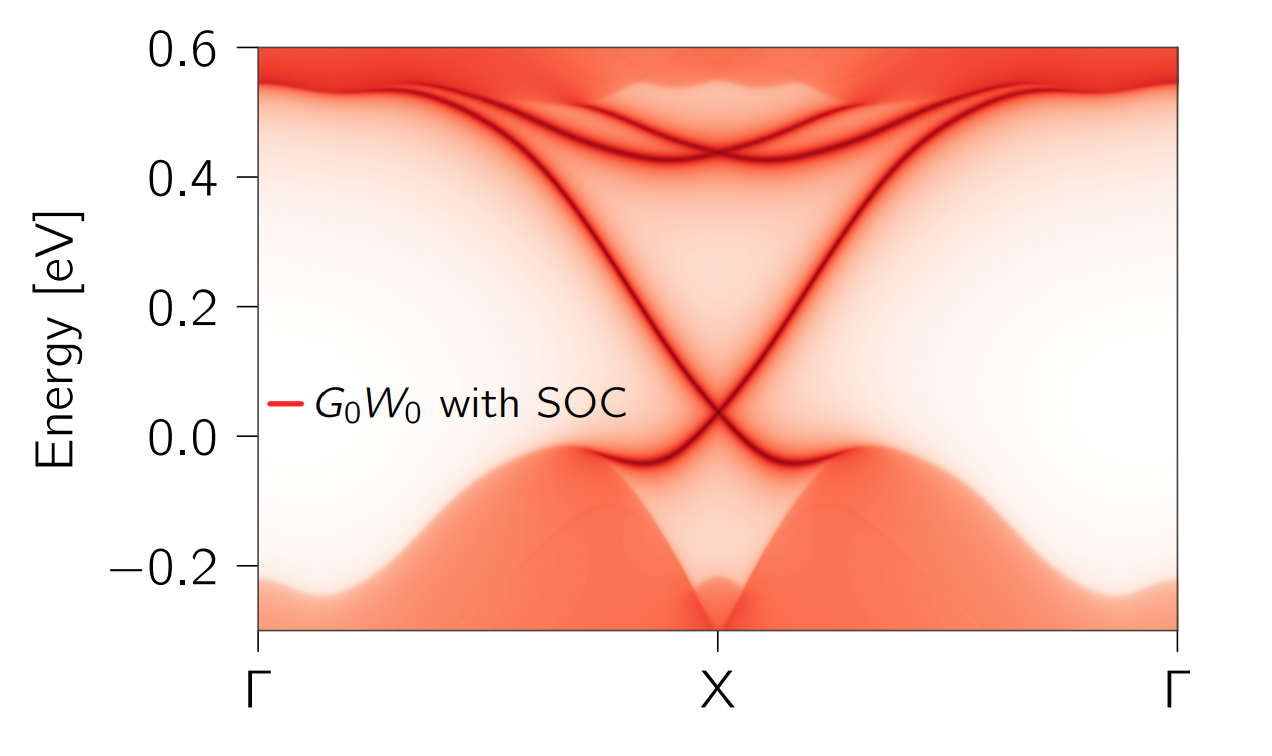
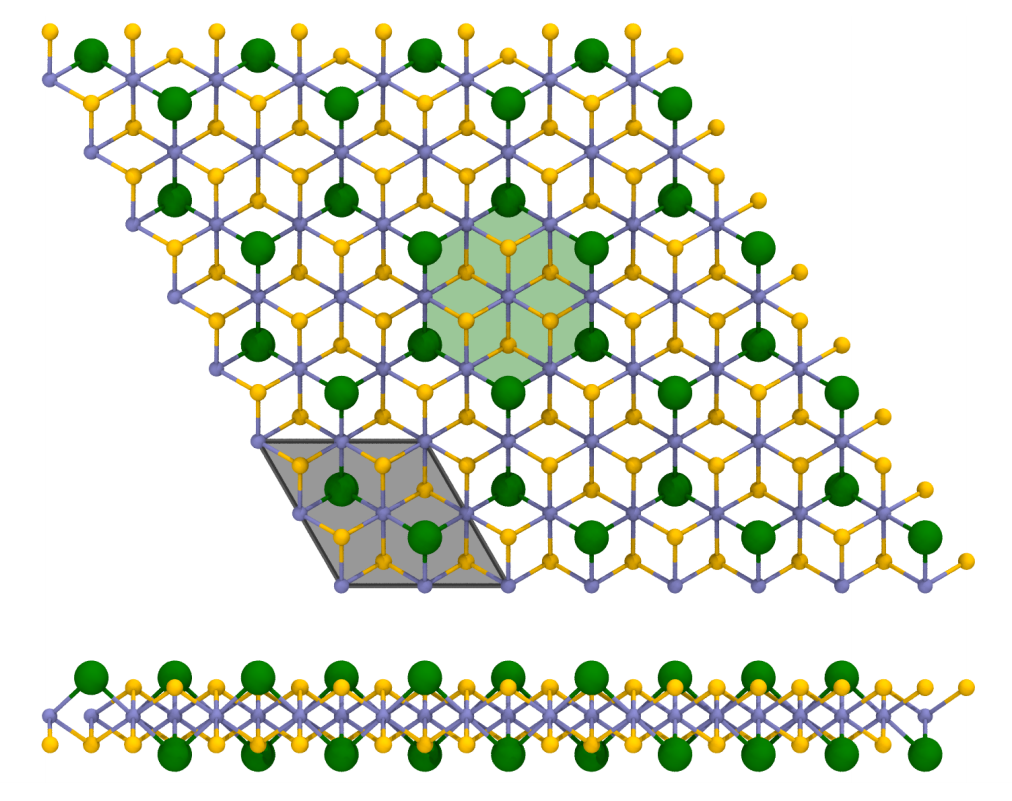
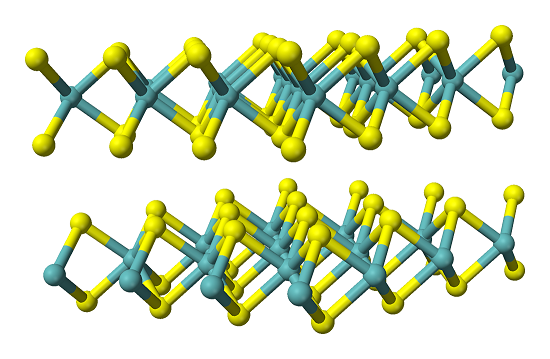
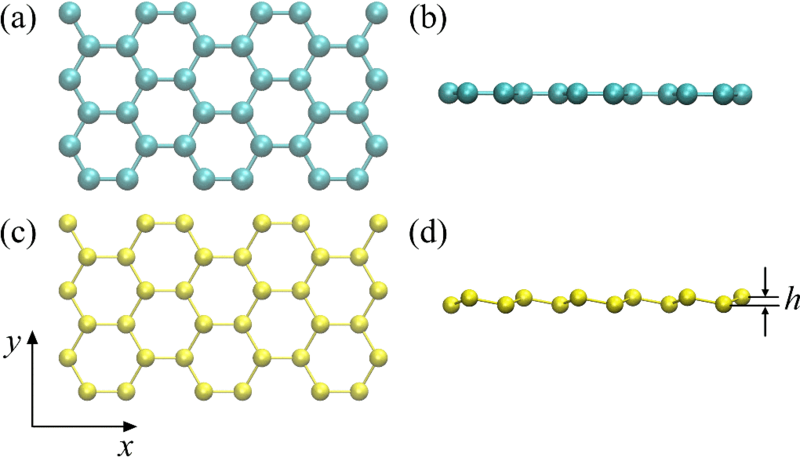
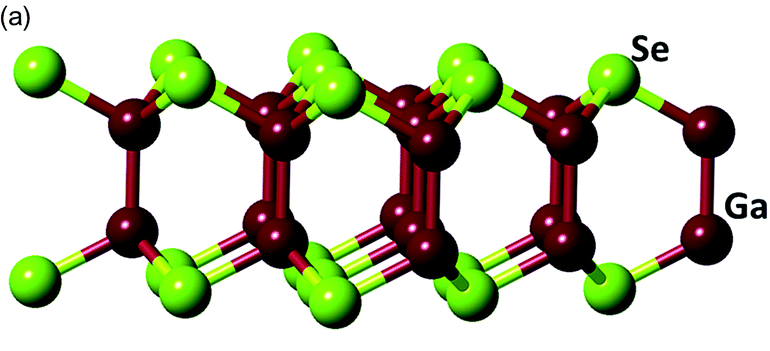
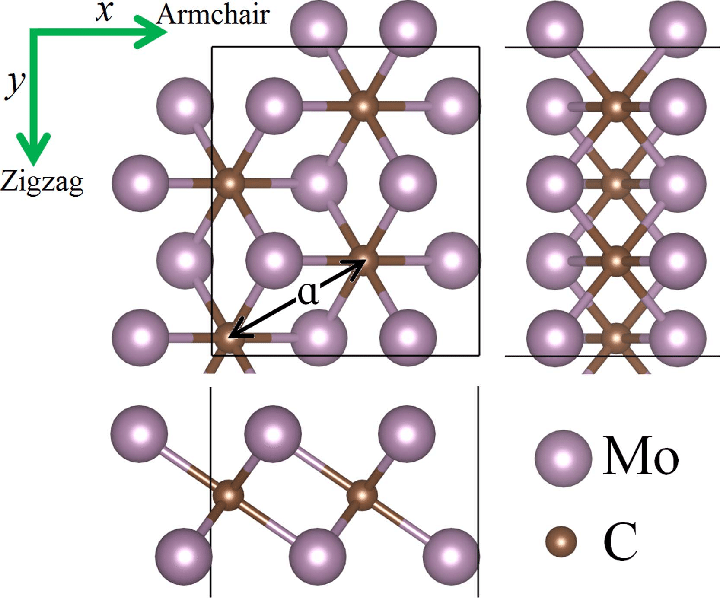
Kukucska Gergő
Kétdimenziós anyagok - motiváció
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
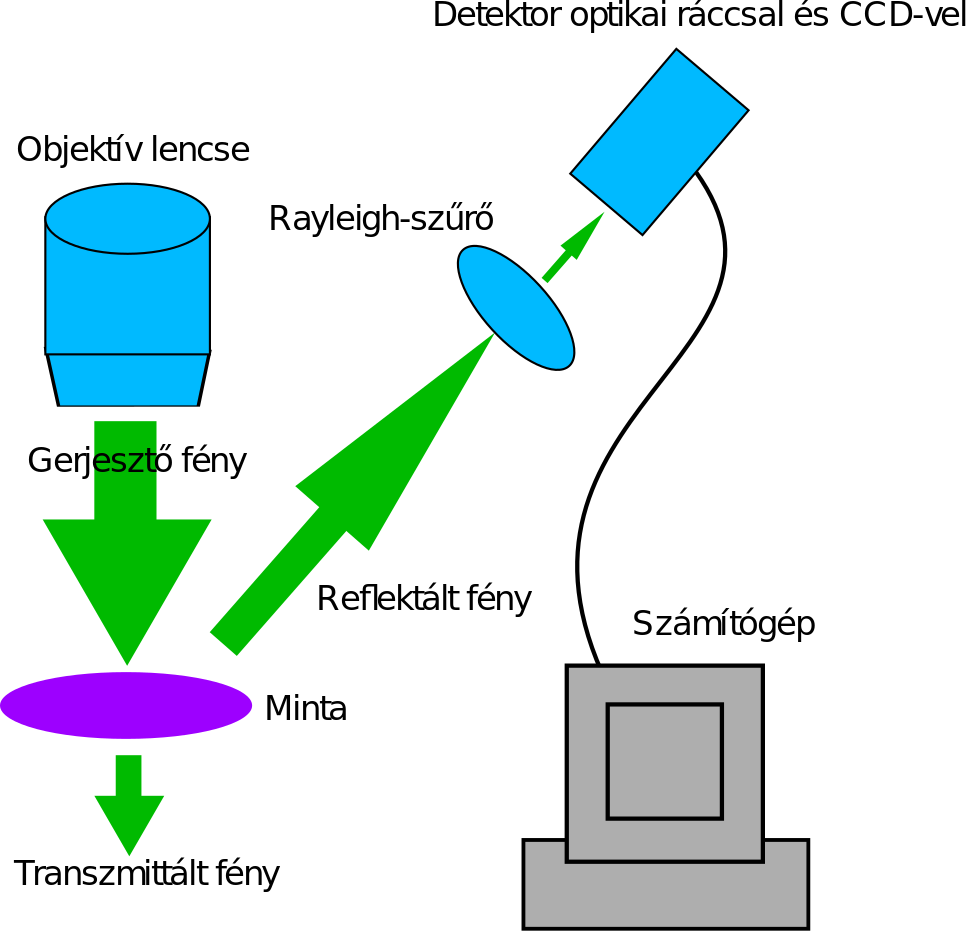
Mérhető mennyiségek:
- Rezgési frekvenciák
- Szerkezeti tulajdonságok
- Elektromos tulajdonságok
- Külső perturbációk
Előnyök:
- Könnyen elvégezhető
- Nem destruktív
- Rezgések vizsgálata egyéb módszerekkel nehézkes
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Mérhető mennyiségek:
- Rezgési frekvenciák
- Szerkezeti tulajdonságok
- Elektromos tulajdonságok
- Külső perturbációk
Előnyök:
- Könnyen elvégezhető
- Nem destruktív
- Rezgések vizsgálata egyéb módszerekkel nehézkes
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Mérhető mennyiségek:
- Rezgési frekvenciák
- Szerkezeti tulajdonságok
- Elektromos tulajdonságok
- Külső perturbációk
Előnyök:
- Könnyen elvégezhető
- Nem destruktív
- Rezgések vizsgálata egyéb módszerekkel nehézkes
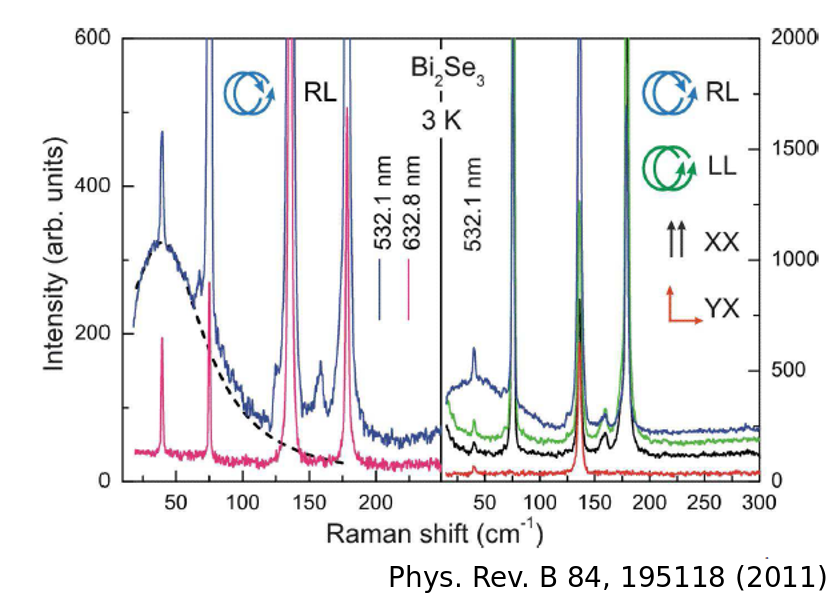
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Mérhető mennyiségek:
- Rezgési frekvenciák
- Szerkezeti tulajdonságok
- Elektromos tulajdonságok
- Külső perturbációk
Előnyök:
- Könnyen elvégezhető
- Nem destruktív
- Rezgések vizsgálata egyéb módszerekkel nehézkes
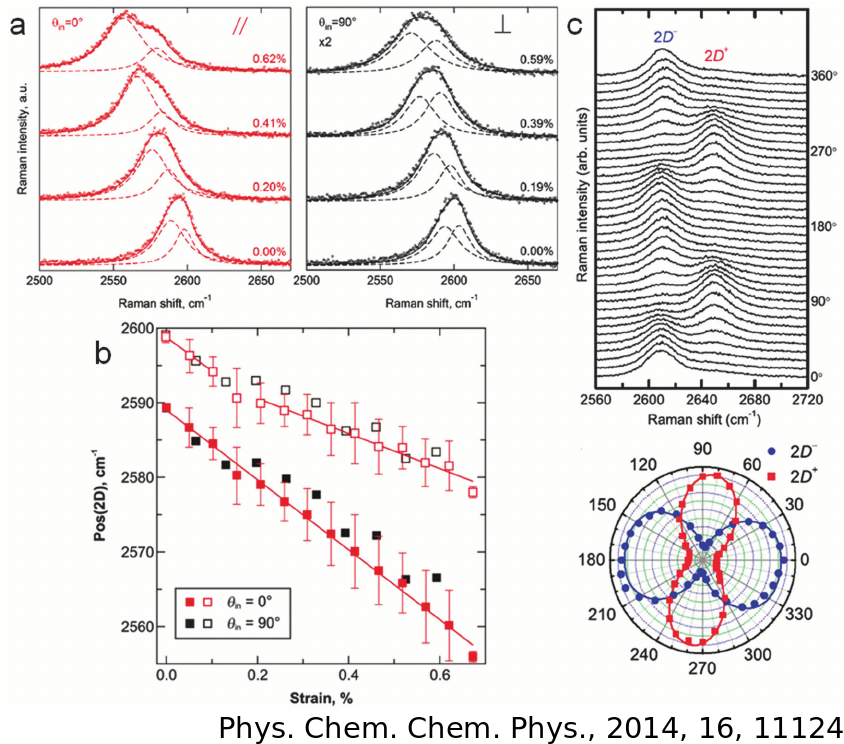
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Időfüggő perturbációszámítás
Placzek-közelítés
(\hat{H_0}+\hat{H}_{e-p}(t)+\hat{H}_{e-ph}(t))\psi=i\hbar\frac{\partial\psi}{\partial t}
\mathbf{P}=\hat{\alpha}({\color{red}\omega_l})\mathbf{E}
Előnyök:
- Polarizálhatóság származtatható első elvekből
- Gyors kis rendszerek esetén
- Soktest-effektusok is figyelembe vehetők (Bethe-Salpeter-egyenlet)
Hátrány:
- Kétfononos, vagy hiba indukált folyamatokat nehéz számolni
Előnyök:
- Kétfononos, vagy hiba indukált folyamatok könnyen leírhatóak
- Nincs klasszikus közelítés
Hátrány:
- Hullámfüggvények és mátrixelemek szükségesek hozzá (általában szoros kötésű közelítés)
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Időfüggő perturbációszámítás
Placzek-közelítés
K_\nu=\sum\limits_{A,B}\frac{\langle i|\hat{H}_{e-p}|A\rangle\langle A|\hat{H}_{e-ph}| B\rangle\langle B|\hat{H}_{e-p}|f\rangle}{(\hbar\omega_l-\epsilon_A-i\gamma)(\hbar\omega_l-\epsilon_B-\hbar\omega_\nu-i\gamma)}
\hat{\alpha}(\omega_l)=\hat{\alpha}_0(\omega_l)+\sum\limits_\nu\frac{\partial\hat{\alpha}(\omega_l)}{\partial Q_\nu}Q_\nu\cos(\omega_\nu t)+\dots
\mathbf{P}_{\textrm{rugalmatlan}}=\sum\limits_\nu\frac{\partial\hat{\alpha}(\omega_l)}{\partial Q_\nu}Q_\nu\mathbf{E}_0\cos((\omega_l-\omega_\nu)t)
K_\nu=\frac{\partial \hat{\alpha}(\omega_l)}{\partial Q_\nu}=\sum\limits_{A,B}\frac{\langle i|\hat{H}_{e-p}|A\rangle\langle A|\hat{H}_{e-ph}| B\rangle\langle B|\hat{H}_{e-p}|f\rangle}{(\hbar\omega_l-\epsilon_A-i\gamma)(\epsilon_A-\epsilon_B-i\gamma)}
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
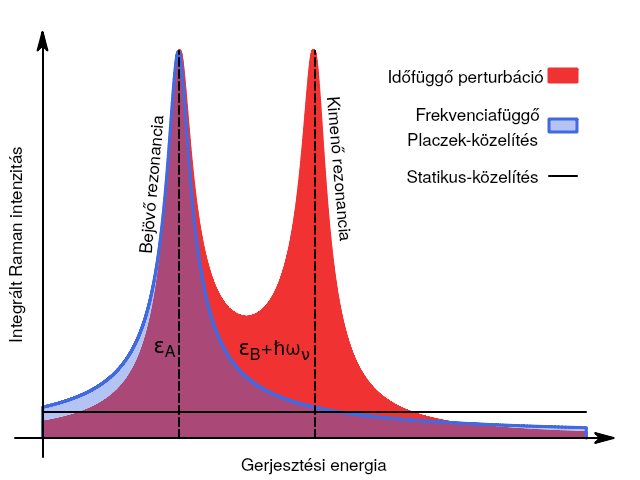
Kukucska Gergő
Raman-spektrumának - elméleti áttekintés
Hogyan lehet meghatározni?
- Szerkezeti és rezgési tulajdonságok ismerete
- Frekvenciafüggő polarizálhatóság meghatározása
- A deriváltjának kiszámítása
Tesztalany - egyrétegű MoS2
- Nem-triviális Raman-spektrum: két aktív és két inaktív csúcs
- Kísérletileg jól ismert Raman-jel
Paraméterek tesztelése:
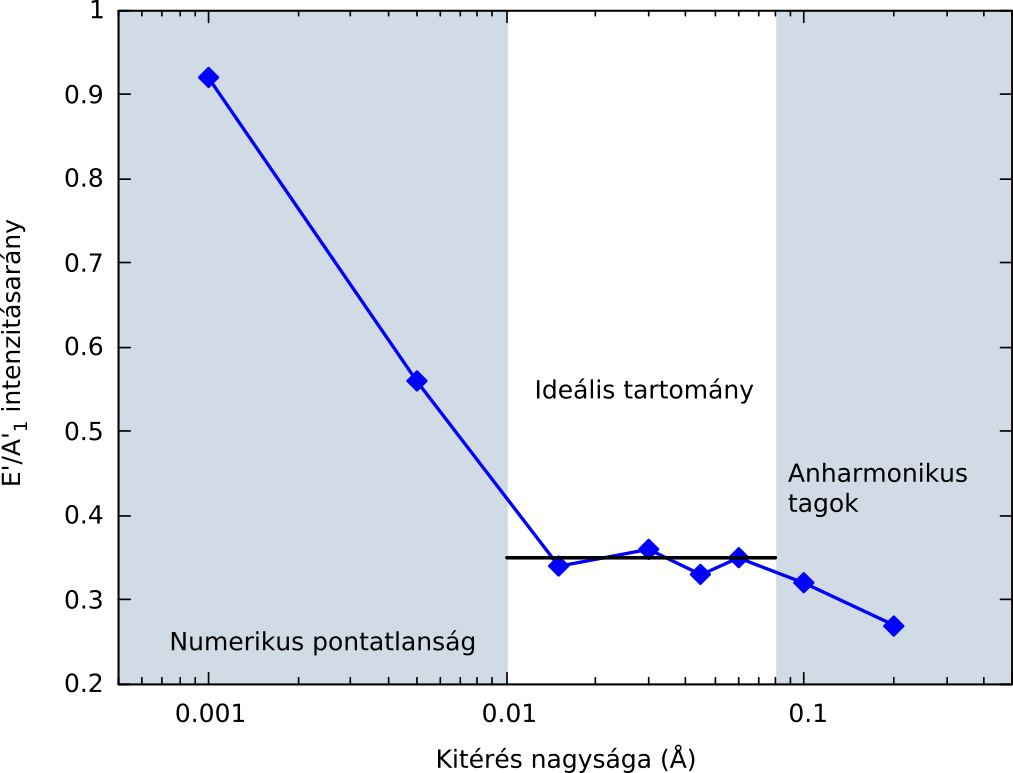
- Véges kitérés nagysága
- Frekvenciafüggő polarizálhatóságot befolyásoló paraméterek
Kukucska Gergő
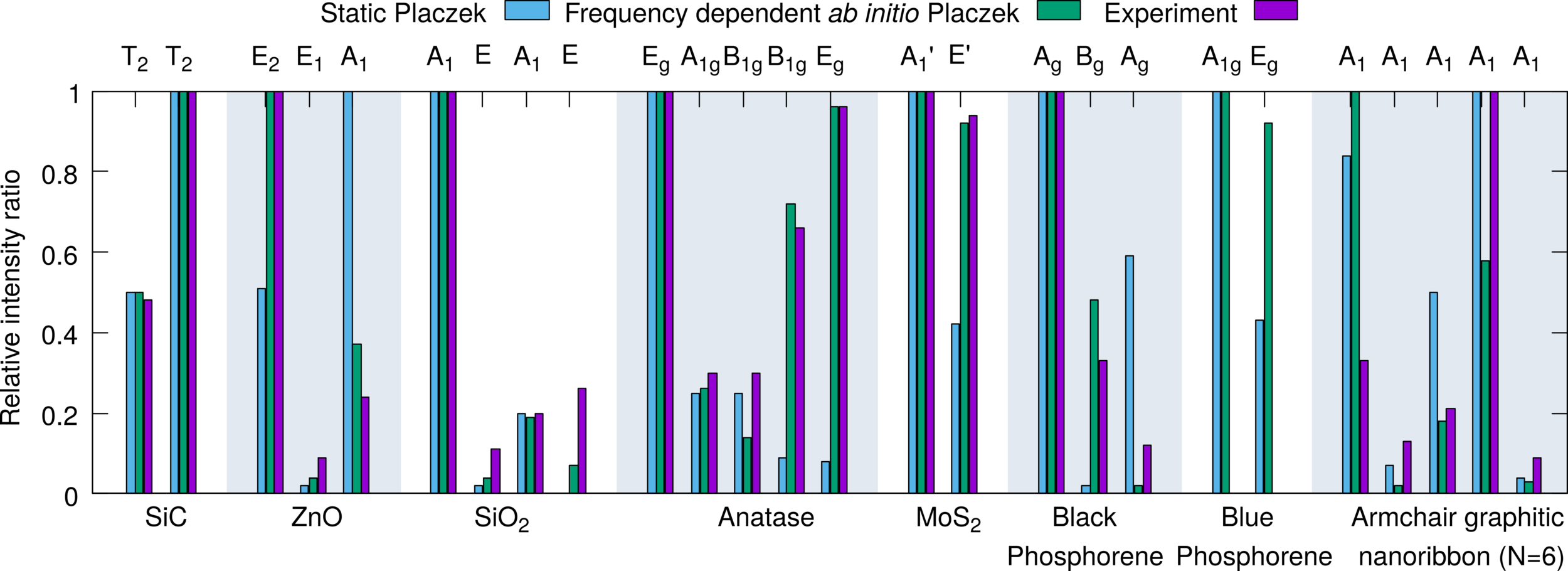
Elméleti vizsgálata - eredmények
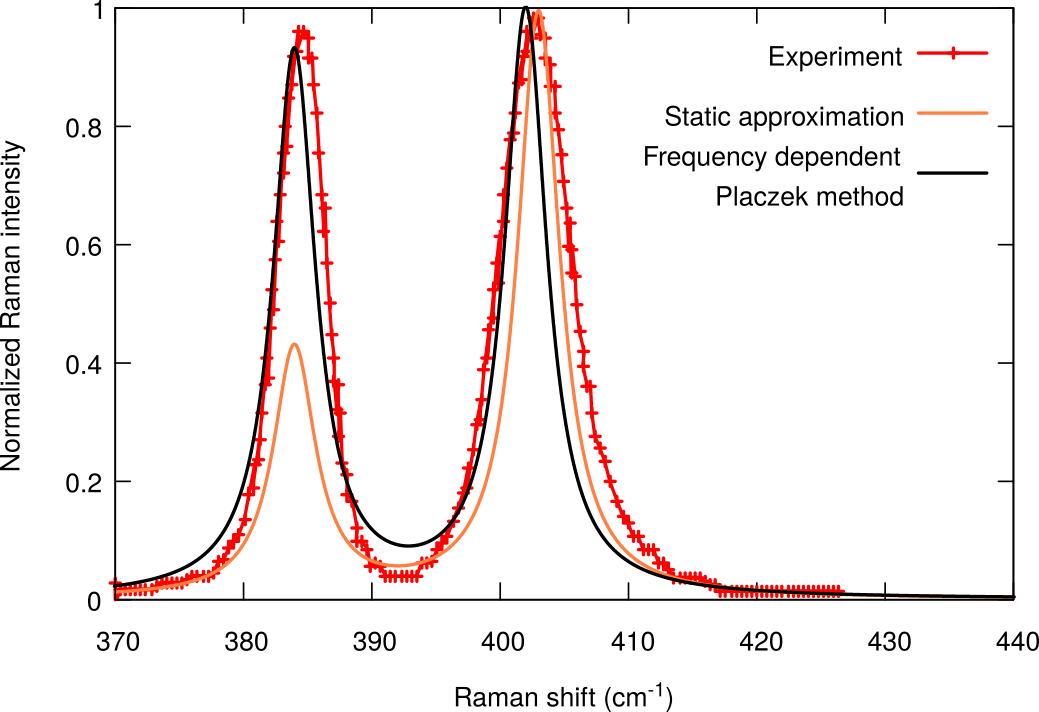
Kukucska Gergő
Elméleti vizsgálata - egyrétegű MoS2
Kukucska Gergő
Elméleti vizsgálata - egyrétegű Fekete foszfor
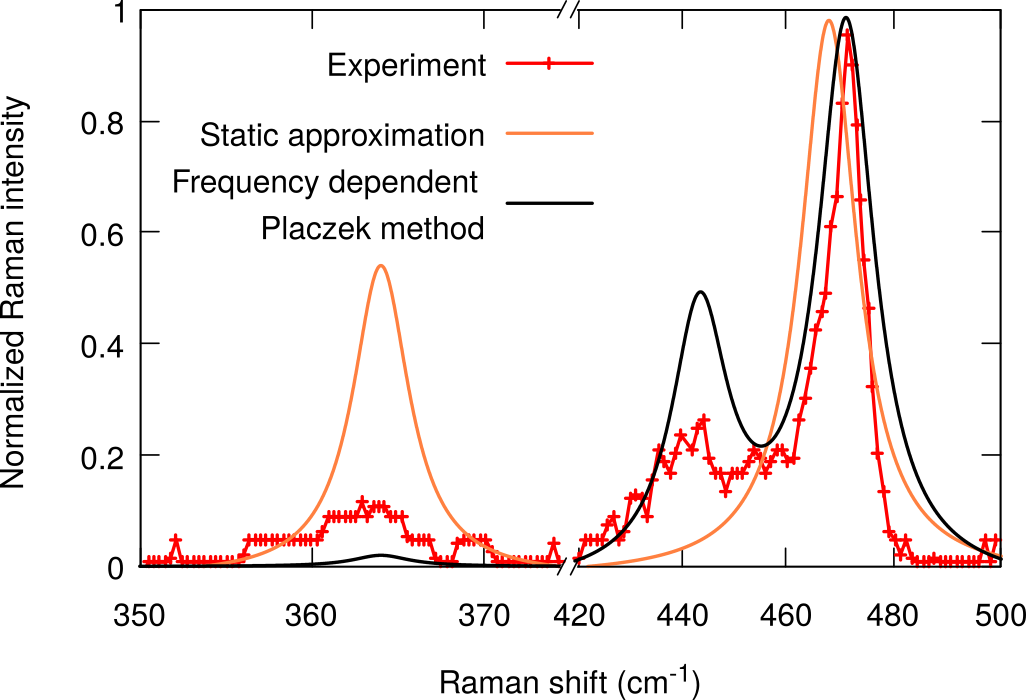
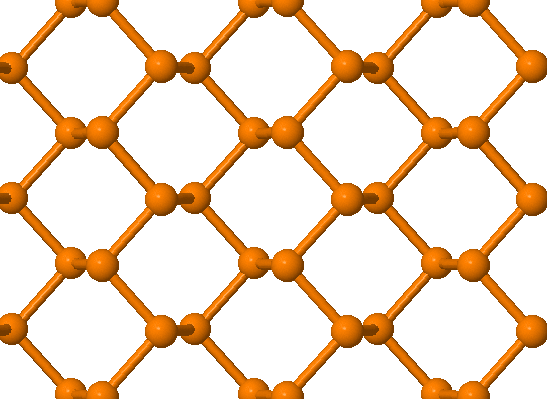
Kukucska Gergő
Elméleti vizsgálata - grafén nanoszalag
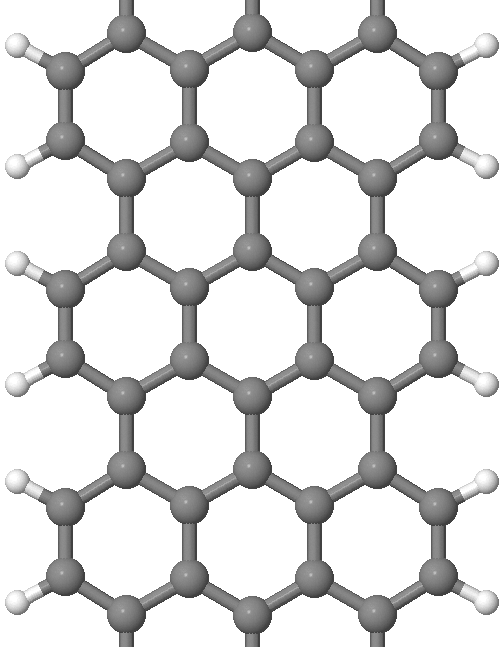
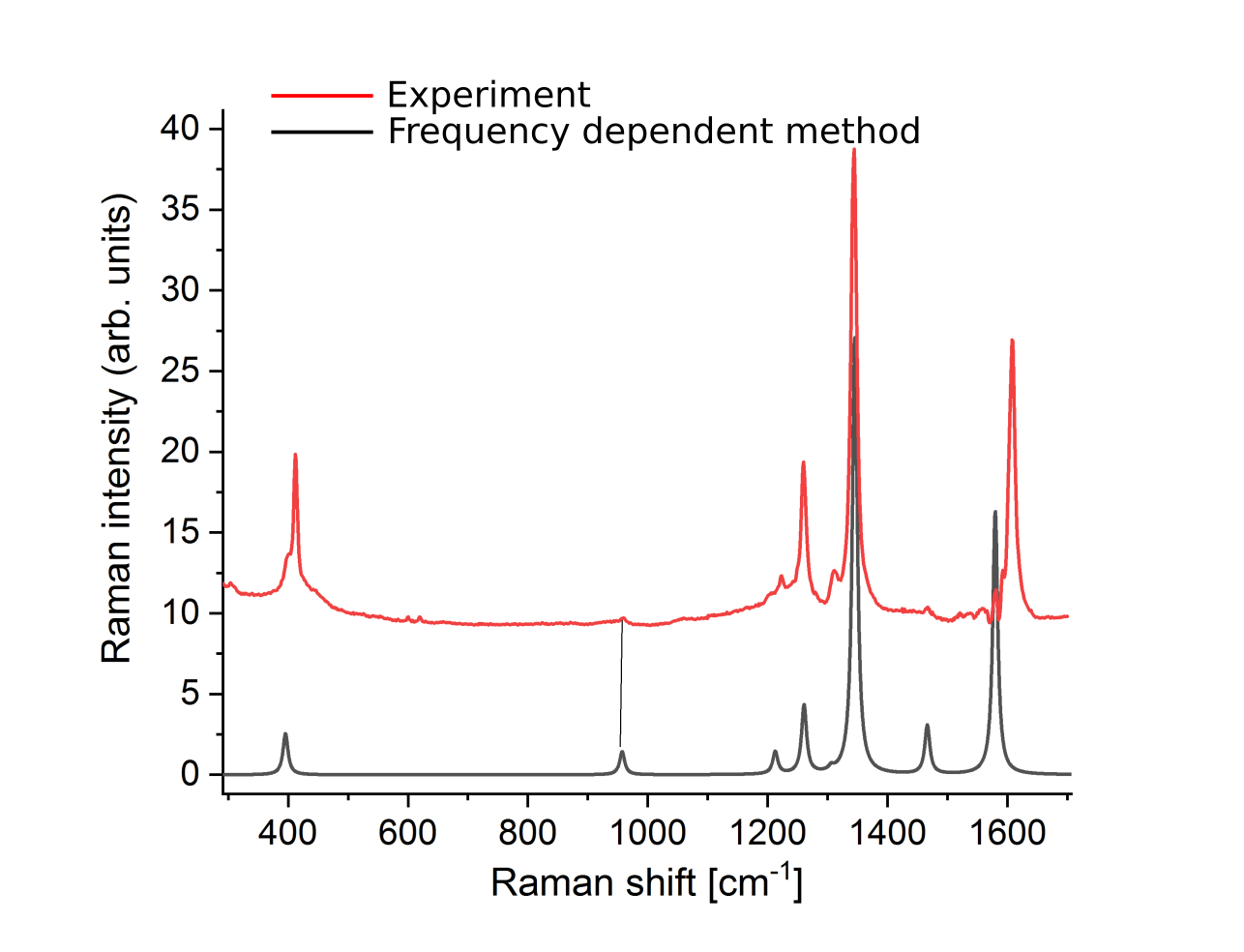
Kukucska Gergő
Összefoglalás:
-
Raman-intenzitások meghatározhatóak a polarizálhatóság deriváltjából
-
Numerikus kitérítések nagysága megegyezik a frekvenciaszámolásnál használttal
-
Soktest-effektusok hozzáadhatóak
-
Kísérletekkel jobb egyezés mint a sztatikus közelítésben
-
''Frequency dependent ab initio resonance Raman spectroscopy'' arXiv:1903.00253
-
''Characterization of epitaxial silicene with Raman spectroscopy''
Phys. Rev. B 98, 075437, 2018
-
''Effect of strain and doping to the Raman spectra of monolayer MoS2''
Phys. Status Solidi B, 254: 1700184, 2017
Kukucska Gergő
Köszönetnyilvánítás
-
Témavezető: Koltai János
-
Kürti Jenő, Zólyomi Viktor, Hans Kuzmany, Nemes-Incze Péter
-
Új Nemzeti Kiválóság Program doktoranduszi és doktorjelölti ösztöndíja (UNKP-2016-3,UNKP-2018-3)
-
ELTE Intézményi Kiválósági Program (1783-3/2018/FEKUTSTRAT)
-
Nemzeti Kutatási, Fejlesztési És Innovációs Hivatal (NKFIH, K-115608 pályázat)
Köszönöm a figyelmet!
UNKP konferencia
By Gergő Kukucska
