
Le tre leggi di newton
Per studiare le tre leggi di Newton dobbiamo introdurre in maniera rigorosa due nuovi concetti!
forza
massa
il concetto di forza
x (m)
x (m)
\hat{\mathbf{i}}
\hat{\mathbf{j}}
\theta
\overrightarrow{F}
F_{\mathrm{y}}
F_{\mathrm{x}}
Una forza che agisce su un oggetto puntiforme è un'interazione che cambia lo stato dell'oggetto su cui agisce.
la risultante delle forze
più forze, che agiscono simultaneamente su un punto materiale, si sommano vettorialmente per ottenere la risultante delle forze
\, \sum_{i} \vec{F_{i}}=\vec{F_{r}} \,
L'idea di massa

Massa come quantità di materia
Kg
massa inerziale
massa come energia
opposizione al cambio di stato di moto
E=mc^{2}

la massa come energia
prima legge di newton
principio d'inerzia
In assenza di forze esterne, un oggetto continuerà a muoversi di moto rettilineo uniforme, o resterà in quiete
si dice sistema di riferimento inerziale un sistema di riferimento in cui la prima legge di newton è valida.
sistemi di riferimento non inerziali: TRaslazioni
si dice sistema di riferimento non inerziale un sistema di riferimento in cui la prima legge di newton non è valida.
sistemi di riferimento non inerziali: rotazioni
si dice sistema di riferimento non inerziale un sistema di riferimento in cui la prima legge di newton non è valida.
seconda legge di newton
forza e accelerazione sono grandezze vettoriali direttamente proporzionali. Il loro rapporto è la massa, costante dipendente dal corpo in esame.
\, \vec{F}=m\vec{a} \,
equazione fondamentale della dinamica
[\mathrm{Kg \cdot m \cdot s^{-2}}]
[N]
seconda legge di newton
\, \sum \vec{F}=m\vec{a} \,
risultante delle forze
[\mathrm{Kg \cdot m \cdot s^{-2}}]
[N]
Rappresentazione delle forze
Diagramma di corpo libero
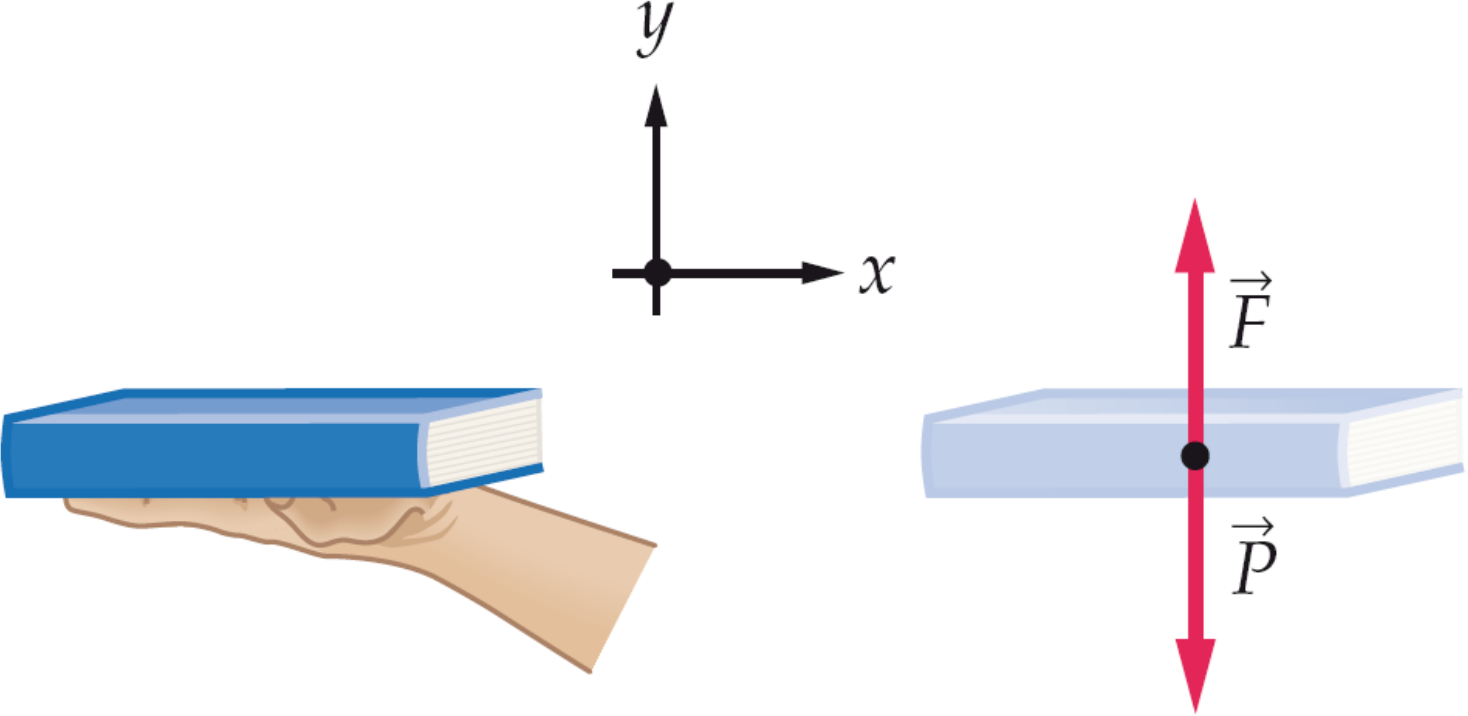
Terza legge di newton
Ad ogni azione corrisponde una reazione uguale e contraria: ossia le forze reciproche fra due corpi sono sempre uguali in module e dirette in versi opposti.
\, \vec{F_{12}}=-\vec{F_{21}} \,
principio di azione e reazione

Terza legge di newton
Love + death + robots: dare una mano
esercizio
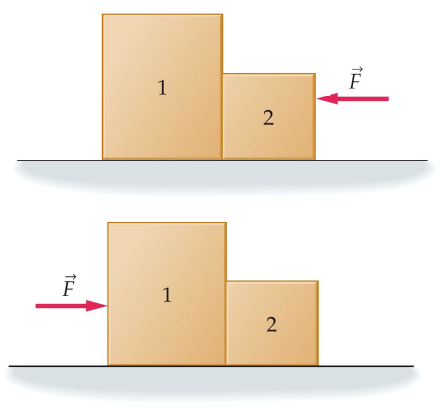
forze: forza gravitazionale
\, \vec{F} = -G \frac{m_{1}m_{2}}{r^{2}} \vec{u_{r}}
legge di gravitazione universale
G = 6.67 \cdot 10^{-11} [N \cdot m^{2} / Kg^{2}]
costante di gravitazione universale
r
\vec{u_{r}}
m_{1}
m_{2}
\vec{F}_{21}
\vec{F}_{12}
satellite in orbita terrestre
\vec{v}
r
2r
forze: forza peso
\, \vec{F} = -G \frac{m_{1}m_{2}}{r^{2}} \vec{u_{r}}
G = 6.67 \cdot 10^{-11} [N \cdot m^{2} / Kg^{2}]
\, M = 5.98 \cdot 10^{24} \, [Kg]
\, R = 6.38 \cdot 10^{6} \, [m]
\, \vec{g} = -G \frac{M}{R^{2}} \vec{u_{r}}
forze: reazione vincolare normale
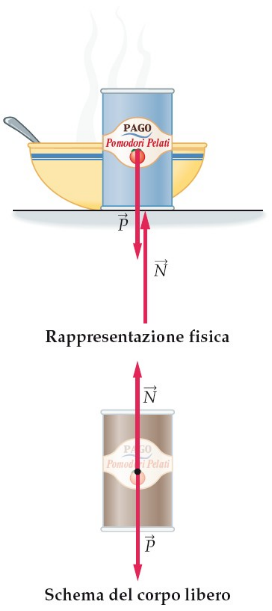
piano inclinato
bilancia in ascensore
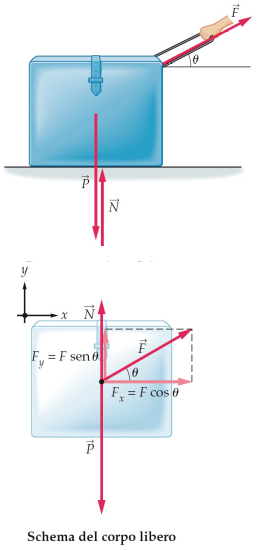
ancora reazioni vincolari normali
forza elastica e moto armonico
\vec{F_{\mathrm{el}}}
x_{0}
\Delta x
k
m


Onda trasversa
Onda longitudinale
forze di attrito
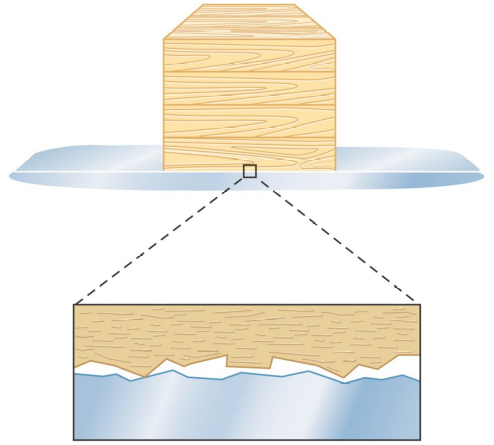
-
attrito statico: se proviamo a muovere un oggetto che è a contatto con una superficie, l’effetto della forza applicata non è immediato, perchè prima dobbiamo “smuoverlo”;
-
Attrito dinamico: quando l’oggetto si mette in moto, l’esperienza insegna che la forza da applicare per mantenere in moto l’oggetto è minore della forza necessaria per smuoverlo;
-
attrito e leggi di newton: se smettiamo di applicare la forza, l’oggetto si ferma. tali osservazioni sembrano contraddire il II principio della dinamica, ma non è così: questi effetti sono dovuti a forze, dette attriti, che si generano nel contatto tra l’oggetto e la superficie e si oppongono al moto.
attrito statico e dinamico:1
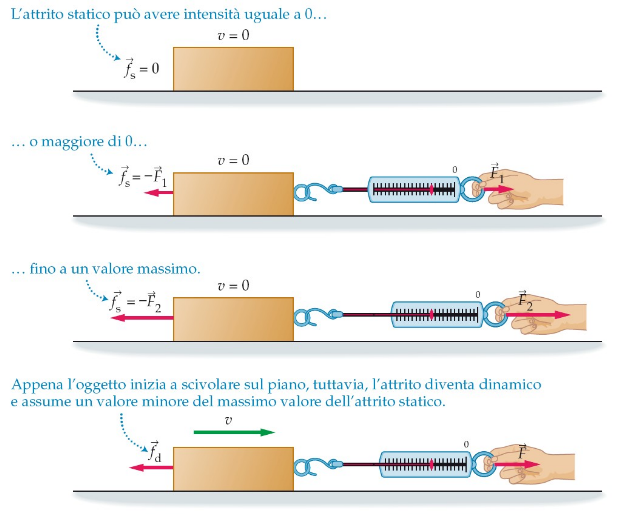
f_{s} \leq \mu_{s} \cdot N
attrito statico
f_{d} = \mu_{d} \cdot N
attrito dinamico
\mu_{s}, \, \mu_{d}
coefficienti di attrito
attrito statico e dinamico:2
F
f_{s,d}
attrito statico e automobili
\vec{F}_{auto}
\vec{F}_{terreno}
pian inclinato con attrito

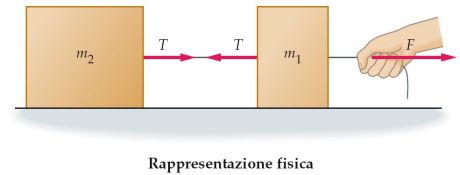
tensione in una fune
Tirando gli estremi di un pezzo di corda, la corda si tende; si dice che nella corda c’è una tensione.
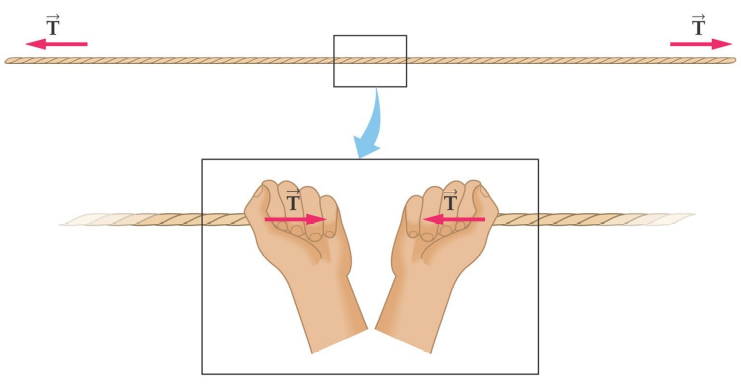
fune ideale
In una corda reale (dotata di massa), la tensione varia da un estremo all’altro a causa del peso della corda
Nel seguito assumeremo che tutte le funi siano ideali, ossia prive di massa ed inestensibili
esercizio
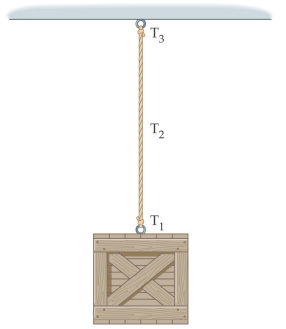
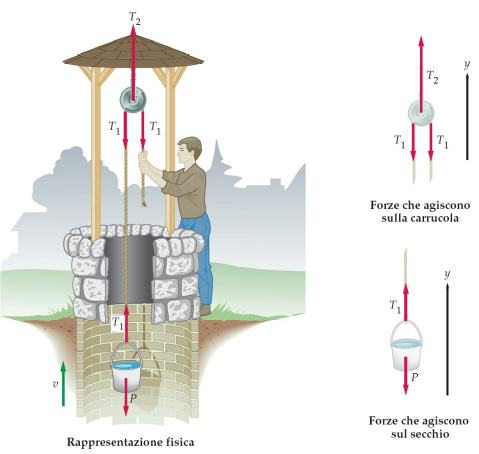
carrucole
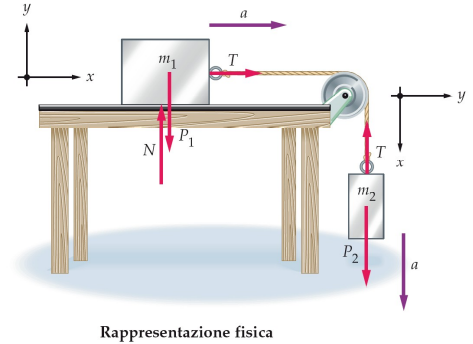
Una carrucola ideale cambia semplicemente la direzione della tensione, senza modificarne l’intensità.

esercizio: equilibrio rispetto alla traslazione
Un oggetto si dice in equilibrio rispetto alla traslazione quando la forza risultante che agisce su di esso è nulla.
forze e moto circolare
per il principio d'inerzia, un moto circolare non può avvenire in assenza di forze
\vec{v}
\vec{a_{\mathrm{N}}}
r
\vec{F}_{cp} = m \cdot \vec{a_{\mathrm{N}}}
\vec{F}_{cp} = \vec{T}
\vec{F}_{cp} = \vec{f}_{s}
\vec{F}_{cp} = \vec{P}
Moto circolare: dosso
\vec{v}
\vec{P}
r



\vec{v}
\vec{P}
\vec{P}
\vec{v}
\vec{P}
Moto circolare: curva parabolica
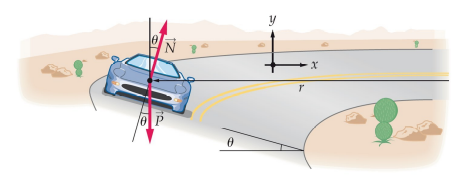
\vec{v}
\vec{a_{\mathrm{N}}}
r
Moto circolare: pendolo conico
\vec{v}
\vec{a_{\mathrm{N}}}
r
\vec{P}
\vec{T}
\theta
Geologia: dinamica
By Giovanni Pellegrini
Geologia: dinamica
- 100



