BAND STRUCTURES
DENSITY OF STATES
SPIN DEGREES OF FREEDOM
[\hat{S}_x,\hat{S}_y]=i \hbar \hat{S}_{z} \\
[\hat{S}_y,\hat{S}_z]=i \hbar \hat{S}_{x} \\
[\hat{S}_z,\hat{S}_x]=i \hbar \hat{S}_{y} \\
[\hat{S}^2,\hat{S}_{x,y,z}]=0
[\hat{L}_x,\hat{L}_y]=i \hbar \hat{L}_{z} \\
[\hat{L}_y,\hat{L}_z]=i \hbar \hat{L}_{x} \\
[\hat{L}_z,\hat{L}_x]=i \hbar \hat{L}_{y} \\
[\hat{L}^2,\hat{L}_{x,y,z}]=0
Angular Momentum
Angular Momentum
Spin
SPIN: EIGENVALUES AND EIGENFUNCTIONS
\begin{dcases}
\hat{S}_z \chi_{s,m_s} = \hbar m_s \chi_{s,m_s} \\[10pt]
\hat{S}^2 \chi_{s,m_s} = \hbar^2 s (s+1) \chi_{s,m_s}
\end{dcases}
with \(s=0,1/2,1,3/2,2,...\)
and \( -s \le m_s \le s\)
The value of the spin is a feature of the elementary particle and it cannot be changed
Fermions: semi-integer
-
Electron: \( s=\frac{1}{2}, m_s=\pm\frac{1}{2} \)
-
Proton: \( s= \frac{1}{2}, m_s=\pm\frac{1}{2} \)
-
Neutron: \( s= \frac{1}{2}, m_s=\pm\frac{1}{2} \)
Bosons: integer
-
Photon: \( s=0, m_s=0 \)
-
Higgs: \( s=0, m_s=0 \)
-
\(W^{+},W^{+},Z^{0}:\) \( s=1, m_s=-1,0,1 \)
SPIN: LABELLING THE ELECTRON EIGENFUNCTIONS
\psi_{n,l,m}(\vec{r})
\varphi_{n,k,m_{s}}(\vec{r})
Hydrogen Atom
Electron in Solid
Quantum Numbers
-
\(n:\) energy
-
\(l:\) angular momentum
-
\(m:\) z-angular momentum
Quantum Numbers
-
\(n:\) energy
-
\(k:\) crystal momentum
-
\(m_s:\) z-spin
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
SPIN DEGREES OF FREEDOM
COUNTING THE AVAILABLE STATES: DENSITY OF STATES
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
THE STARTING POINT: A 1D PERIODIC LATTICE OF ATOMS

BORN VON-KARMAN BOUNDARY CONDITIONS


a
x
L
\varphi_{n,k,m_{s}}(x) = \varphi_{n,k,m_{s}}(x+L)
\begin{align*}
e^{i k x} f_{n,k,m_s}(x) & = e^{i k (x+L)} f_{n,k,m_s}(x+L) \\
& = e^{i k x} e^{i k L} f_{n,k,m_s}(x)
\end{align*}
e^{i k L} = 1
k = n \frac{2 \pi}{L}, \, n=0,1,2, \ldots
COUNTING THE AVAILABLE STATES: DENSITY OF STATES
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
g(E) = \frac{1}{V}\frac{dN}{dE} = \frac{\text{Number of states}}{\text{Unit of energy}}
N = 2 * \frac{\frac{2 \pi}{a}}{\frac{2 \pi}{L}} = 2 \frac{L}{a} = 2 * (\text{Number of unit cells})
DENSITY OF STATES: FREE ELECTRON GAS
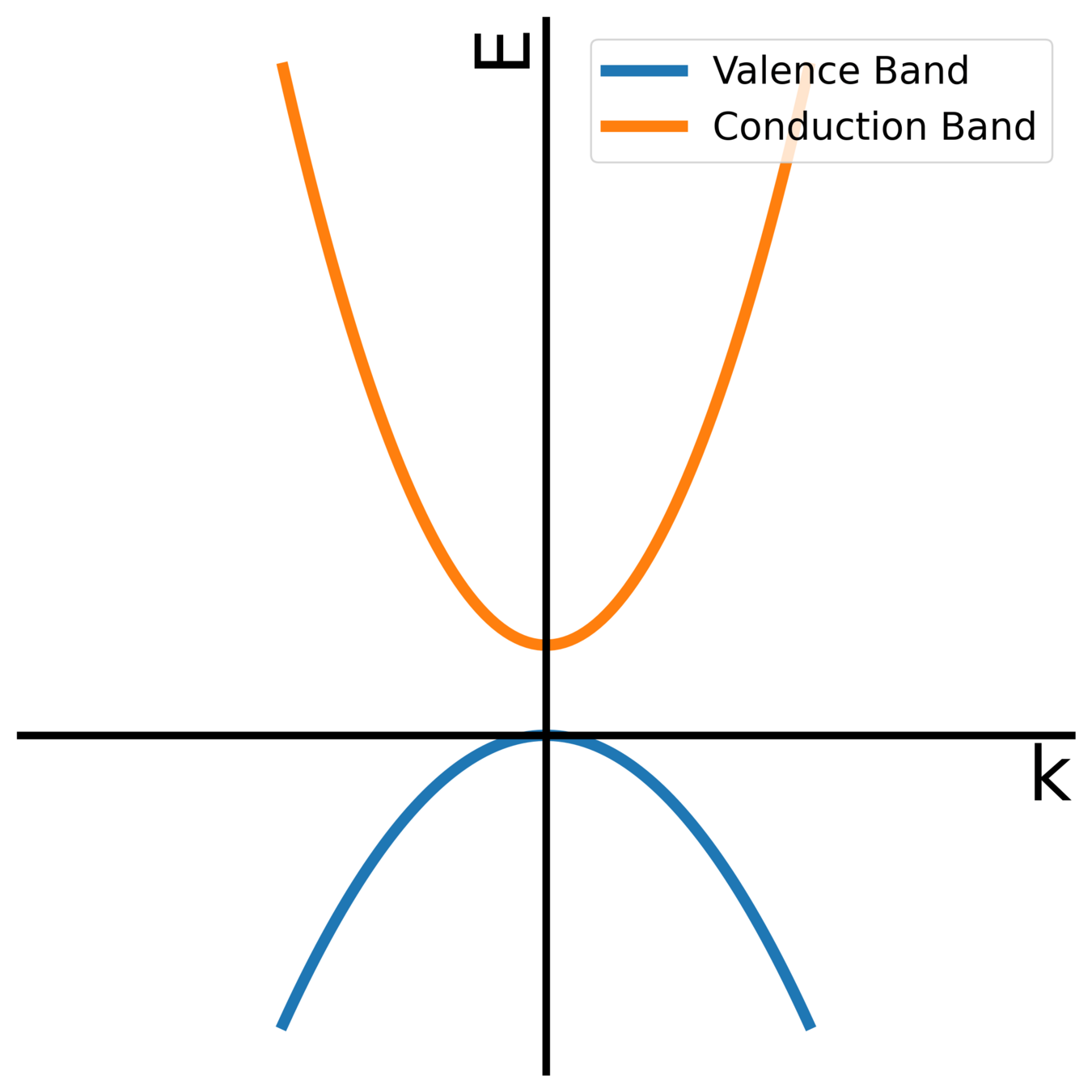
\begin{dcases}
\frac{1}{m_{v}^*}=-\frac{1}{\hbar^2} \frac{\partial^2 E_{v}}{\partial k^2} \\
\frac{1}{m_{c}^*}=\frac{1}{\hbar^2} \frac{\partial^2 E_{c}}{\partial k^2}
\end{dcases}
\begin{dcases}
E_v(k)=\frac{p_v^2}{2 m_v^*} \\
E_c(k)=E_g + \frac{p_c^2}{2 m_c^*}
\end{dcases}
Effective mass
"Free" Electrons
DENSITY OF STATES: FREE ELECTRON GAS

\begin{dcases}
\frac{1}{m_{v}^*}=-\frac{1}{\hbar^2} \frac{\partial^2 E_{v}}{\partial k^2} \\
\frac{1}{m_{c}^*}=\frac{1}{\hbar^2} \frac{\partial^2 E_{c}}{\partial k^2}
\end{dcases}
\begin{dcases}
E_v(k)=\frac{p_v^2}{2 m_v^*} \\
E_c(k)=E_g + \frac{p_c^2}{2 m_c^*}
\end{dcases}
Effective mass
"Free" Electrons
A FREE PARTICLE IN THREE DIMENSIONS
H(\vec{r},\vec{p}) = \frac{\vec{p}^2}{2 m} = \frac{p_x^2}{2 m} + \frac{p_y^2}{2 m} +\frac{p_z^2}{2 m}
\hat{H}(\vec{r},\hat{\vec{p}}) = \frac{\hat{p}_x^2}{2 m} + \frac{\hat{p}_y^2}{2 m} +\frac{\hat{p}_z^2}{2 m}
\hat{H} = -\bigg(\frac{\hbar^2}{2 m}\frac{\partial^2}{\partial x ^2}
+\frac{\hbar^2}{2 m}\frac{\partial^2}{\partial y ^2}
+\frac{\hbar^2}{2 m}\frac{\partial^2}{\partial z ^2} \bigg)
= -\frac{\hbar^2}{2 m} \vec{\nabla}^2
N FREE ELECTRONS IN THREE DIMENSIONS
\hat{H}\left(\vec{r}_1, \vec{r}_2, \ldots \vec{r}_N\right)=-\sum_{i=1}^N \frac{\hbar^2}{2 m} \nabla_i^2=\sum_{i=1}^N \hat{H}_i
\psi_{\vec{k}}(x, y, z)=\psi_{\vec{k}}(\vec{r})=\frac{1}{V^{1 / 2}} e^{i \vec{k} \cdot \vec{r}}
=\frac{1}{V^{1 / 2}} e^{i (k_x x + k_y y +k_z z)}
E_{\vec{k}}=\frac{\hbar^2\left(k_x^2+k_y^2+k_z^2\right)}{2 m}
BORN VON-KARMAN BOUNDARY CONDITIONS
IN THREE DIMENSIONS
\begin{align*}
\psi_{\vec{k}}(x + L, y, z) & = \psi_{\vec{k}}(x , y, z) \\
& \Downarrow \\
e^{i (k_x (x+L) + k_y y +k_z z)} & = e^{i k_x L }e^{i (k_x x + k_y y +k_z z)} \\
& \Downarrow \\
e^{i k_x L } & = 1 \\
& \Downarrow \\
k_x = l \frac{2 \pi}{L} &\text{ with } l \in \mathbb{Z}
\end{align*}
\begin{align*}
\psi_{\vec{k}}(x, y + L, z) & = \psi_{\vec{k}}(x , y, z) \\
& \Downarrow \\
e^{i (k_x x + k_y (y+L) +k_z z)} & = e^{i k_y L }e^{i (k_x x + k_y y +k_z z)} \\
& \Downarrow \\
e^{i k_y L } & = 1 \\
& \Downarrow \\
k_y = m \frac{2 \pi}{L} &\text{ with } m \in \mathbb{Z}
\end{align*}
\begin{align*}
\psi_{\vec{k}}(x, y, z + L) & = \psi_{\vec{k}}(x , y, z) \\
& \Downarrow \\
e^{i (k_x x + k_y y +k_z (z+L)} & = e^{i k_z L }e^{i (k_x x + k_y y +k_z z)} \\
& \Downarrow \\
e^{i k_z L } & = 1 \\
& \Downarrow \\
k_z = n \frac{2 \pi}{L} &\text{ with } n \in \mathbb{Z}
\end{align*}
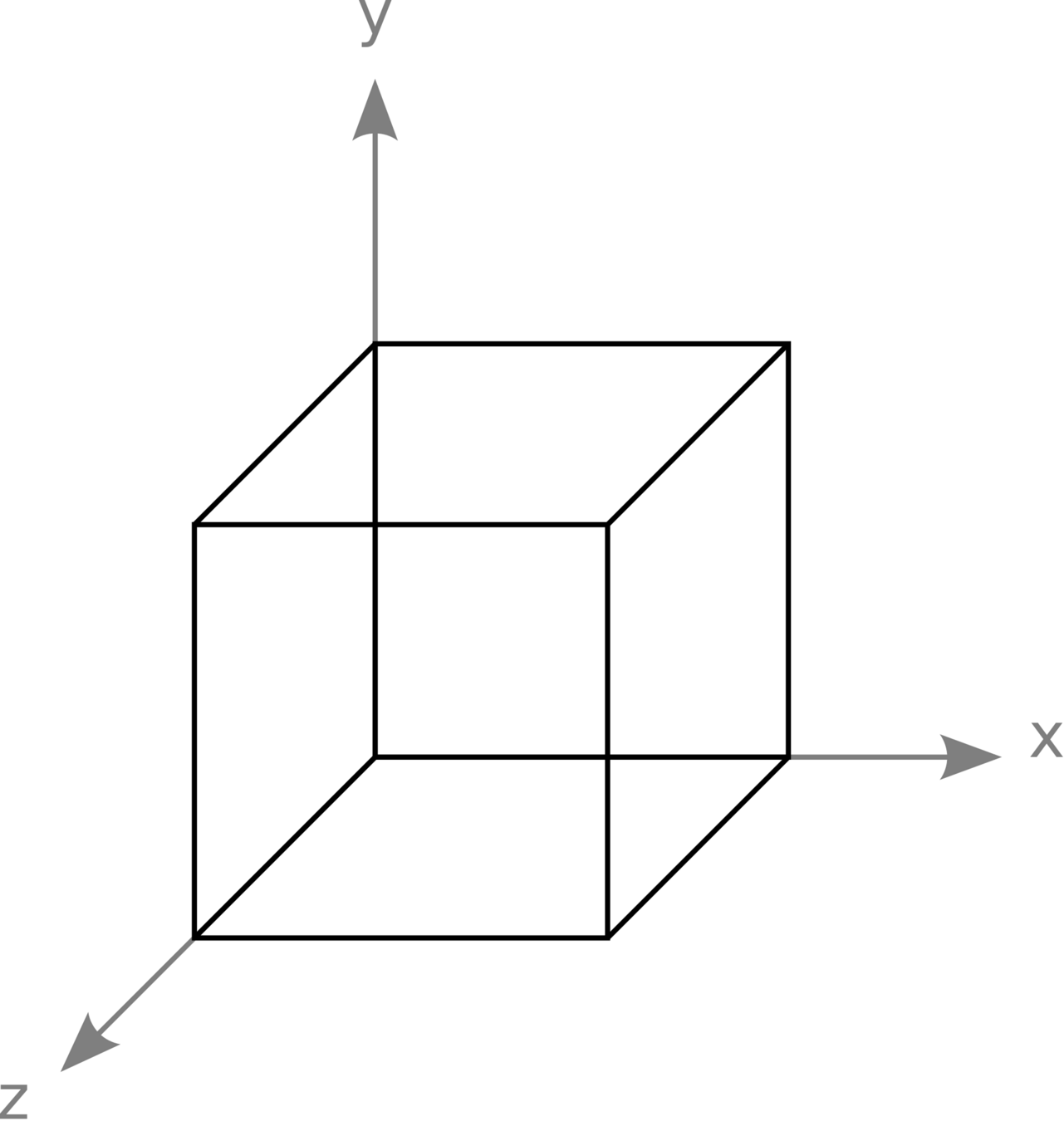
L
L
L
COUNTING THE STATES
k_x = l \frac{2 \pi}{L} \text{ with } l \in \mathbb{Z}
k_z = n \frac{2 \pi}{L} \text{ with } n\in \mathbb{Z}
k_y = m \frac{2 \pi}{L} \text{ with } m \in \mathbb{Z}
E = \frac{\hbar |\vec{k}|^2}{2m}
k_x
k_y
\frac{2 \pi}{L}
\frac{2 \pi}{L}
k+dk
k
COUNTING THE STATES
k_x
k_y
\frac{2 \pi}{L}
\frac{2 \pi}{L}
k+dk
k
\begin{dcases}
V_{sphere}(k) = 2*\frac{4}{3} \pi k^3 \\[10pt]
V_{cell} = \bigg( \frac{2 \pi}{L} \bigg)^3
\end{dcases}
N(k) = \frac{V_{sphere}(k)}{V_{cell}} = \frac{V}{3 \pi^2} k^3
N(E) = \frac{V}{3 \pi^2} \left(\frac{2 m E}{\hbar^2}\right)^{3 / 2}
k = \sqrt{\frac{2 m E}{\hbar^2}}
DENSITY OF STATES FOR A 3D FREE ELECTRON GAS
k_x
k_y
\frac{2 \pi}{L}
\frac{2 \pi}{L}
k+dk
k
g(E) = \frac{1}{V}\frac{dN(E)}{dE} = \frac{m}{\hbar^2 \pi^2} \sqrt{\frac{2 m E}{\hbar^2}}
FERMI ENERGY FOR A 3D FREE ELECTRON GAS
k_x
k_y
\frac{2 \pi}{L}
\frac{2 \pi}{L}
k+dk
k
N(E) = \frac{V}{3 \pi^2} \left(\frac{2 m E}{\hbar^2}\right)^{3 / 2}
E_{F} = \frac{\hbar^2}{2m} \left( \frac{3 N \pi^2}{V} \right)^{\frac{2}{3}} \\
FERMI ENERGY AND THE CHEMICAL POTENTIAL
\begin{dcases}
\mathrm{d} U=T \mathrm{~d} S-P \mathrm{~d} V+\sum_{i=1}^n \mu_i \mathrm{~d} N_i \\
\mu_i=\left(\frac{\partial U}{\partial N_i}\right)_{S, V, N_{j \neq i}}
\end{dcases}
E_{F} = \frac{\hbar^2}{2m} \left( \frac{3 N \pi^2}{V} \right)^{\frac{2}{3}} \\
The chemical potential \(\mu\) is the energy that can be absorbed or released due to a change of the particle number
\begin{dcases}
\mathrm{d} F=-S \mathrm{~d} T-p \mathrm{~d} V + \sum_{i=1}^n \mu_i \mathrm{~d} N_i \\
\mu_i=\left(\frac{\partial F}{\partial N_i}\right)_{T, V, N_{j \neq i}}
\end{dcases}
F \equiv U-T S,
Helmholtz Free Energy
E_{F} \simeq \mu
E_{F}
FILLING THE AVAILABLE STATES
3 states - 2 particles example
Maxwell-Boltzmann
Bose-Einstein
Fermi-Dirac
A
A
A
A
B
B
B
B
A
B
B
A
A
B
A
B
A
B
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
\sigma_{1} = \{ n_1, k_1, m_{s_1} \},
\sigma_{2} = \{ n_2, k_2, m_{s_2} \},
\sigma_{3} = \{ n_3, k_3, m_{s_3} \}
\sigma_1
\sigma_2
\sigma_3
\sigma_1
\sigma_2
\sigma_3
\sigma_1
\sigma_2
\sigma_3
9 microstates \(\mathcal{S}\)
6 microstates \(\mathcal{S}\)
3 microstates \(\mathcal{S}\)
BOSE - EINSTEIN CONDENSATION
A
A
\sigma_1
\ldots
\sigma_N
A
A
A
A
A
A
A
A
A
A
FILLING THE AVAILABLE STATES
N electrons
\begin{dcases}
N \text{ electrons} \\
\sigma_{s} = \{ n_s, k_s, m_{s_s} \} \\
E_s \Leftrightarrow \sigma_{s} \\
n_s =0,1 \Rightarrow \text{Occupation number} \\
\mathcal{S} \Rightarrow \text{Microstate}
\end{dcases}
\mathcal{S} \text{ Microstate}
E_{\mathcal{S}} = \sum_{s=1}^{N} n_s E_s
PROBABILITY OF A MICROSTATE
and average occupational probability \( \overline{n}_s \)
\mathcal{S} \text{ Microstate}
E_{\mathcal{S}} = \sum_{s=1}^{N} n_s E_s
\mathcal{P}(\mathcal{S})=\frac{e^{-\frac{E_{\mathcal{S}}}{k_B T}}}{\sum\limits_{\mathcal{All \, S}} e^{-\frac{E_{\mathcal{S}}}{k_B T}}}
\overline{n}_s = \sum\limits_{\mathcal{All \, S}} n_s(\mathcal{S}) \mathcal{P}(\mathcal{S})
\overline{n}_s?
\bar{n}_s(E_s) =\frac{1}{e^{\frac{E_s-\mu}{k_B T}}+1} = \frac{1}{e^{\frac{E_s-E_{F}}{k_B T}}+1}
FERMI DIRAC STATISTICS
\bar{n}_s(E_s) =\frac{1}{e^{\frac{E_s-\mu}{k_B T}}+1} = \frac{1}{e^{\frac{E_s-E_{F}}{k_B T}}+1}
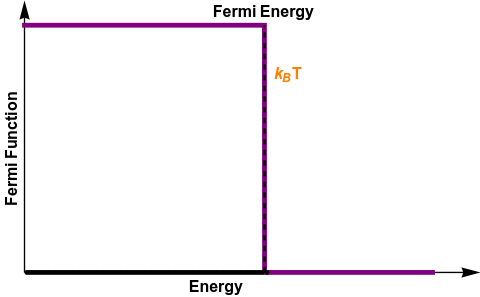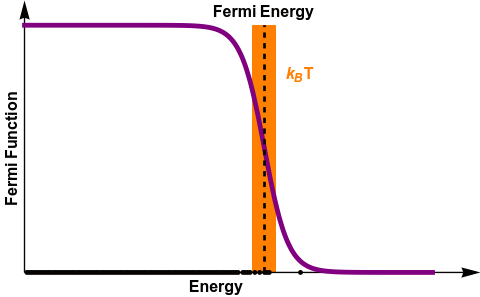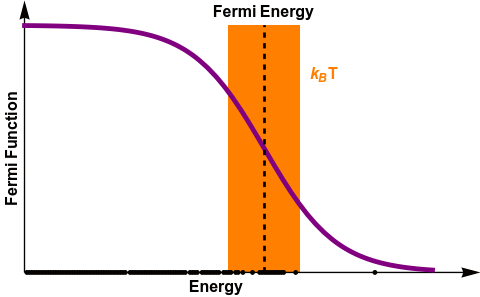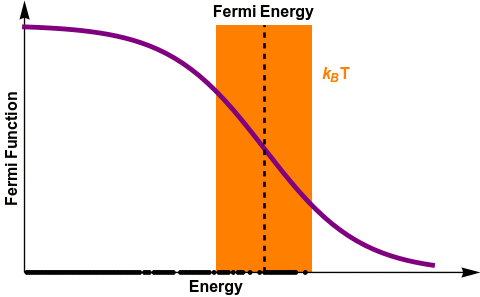
A NEW LOOK AT THE BANDS
k
E



-\frac{g}{2}
\frac{g}{2}
E_g
x
E
A NEW LOOK AT THE BANDS
x
E
E_F
x
E
E_F
Metal
Insulator
A NEW LOOK AT THE BANDS
x
E
E_F
Semiconductor, T=0 K
Semiconductor, T>0 K
x
E
E_F
LOOKING BACK AT THE PERIODIC TABLE

Semiconductors
GROUP IV SEMICONDUCTORS



Si
7
28.085
Silicon
E_g = 5.5 \, eV
E_g = 1.14 \, eV
E_g = 0.67 \, eV
III-V SEMICONDUCTORS

GaN

GaAs
E_g = 3.4 \, eV
E_g = 1.42 \, eV
II-VI SEMICONDUCTORS
CdS
ZnO
E_g = 2.42 \, eV
E_g = 3.73 \, eV


ELECTRONIC AND OPTICAL PROPERTIES
REFRACTIVE INDEX
CdS
ZnO
Real
\begin{dcases}
n = \text{ Real refractive index} \\[10pt]
k_n = \frac{2 \pi n}{\lambda} \\[10pt]
v = \frac{\omega}{k_n} = \frac{c}{n}
\end{dcases}
Complex
\begin{dcases}
n_c = n + i\kappa = \text{ Complex refractive index} \\[10pt]
k_n = \frac{2 \pi n}{\lambda} \\[10pt]
v = \frac{\omega}{k_n} = \frac{c}{n}
\end{dcases}
ELECTRONIC AND OPTICAL PROPERTIES
REFRACTIVE INDEX
CdS
ZnO
\begin{aligned}
\mathbf{E}(x, t) & =\operatorname{Re}\left[\mathbf{E}_0 e^{i(k_c x-\omega t)}\right] \\
& =\operatorname{Re}\left[\mathbf{E}_0 e^{i\left(2 \pi(n+i \kappa) x / \lambda_0-\omega t\right)}\right] \\
& =e^{-2 \pi \kappa x / \lambda_0} \operatorname{Re}\left[\mathbf{E}_0 e^{i(k_n x-\omega t)}\right]
\end{aligned}
The imaginary part \( \kappa \) of the refractive index is responsible for the absorption of light inside the material.
ELECTRONIC AND OPTICAL PROPERTIES
REFRACTIVE INDEX
CdS
ZnO
HOW MANY ELECTRONS AND HOLES IN THE BANDS?
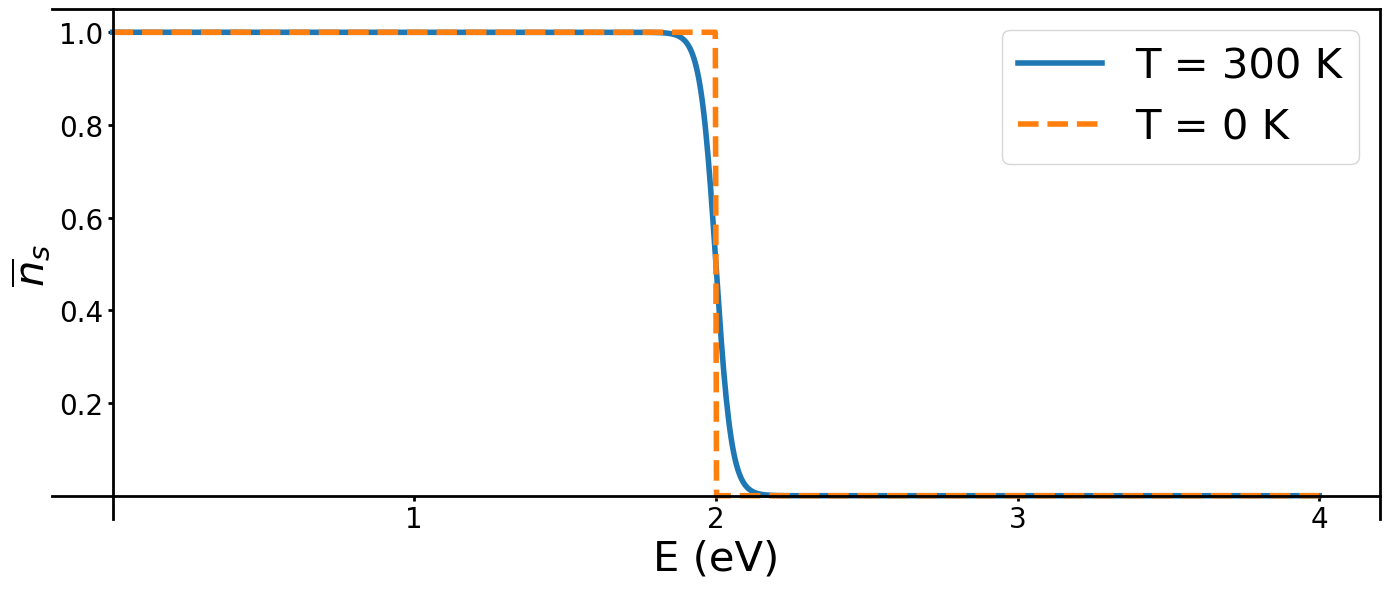
OCCUPATION PROBABILITY FOR SILICON
E_g \simeq 1.1 \, eV
E_f \simeq 0.55 \, eV
k_{B}T \simeq 0.025 \, eV \, \text{at T=300 K}
\overline{n}_s \simeq 10^{-10}
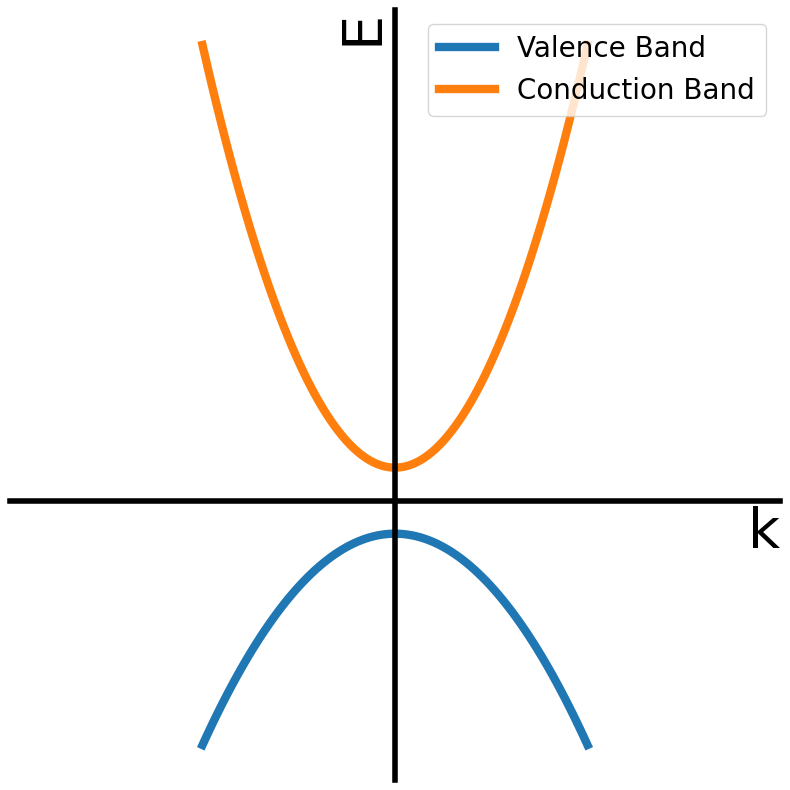
E_g
E_f
OCCUPATION PROBABILITY FOR SILICON
\begin{dcases}
\frac{1}{m_{v}^*}=-\frac{1}{\hbar^2} \frac{\partial^2 E_{v}}{\partial k^2} \\
\frac{1}{m_{c}^*}=\frac{1}{\hbar^2} \frac{\partial^2 E_{c}}{\partial k^2}
\end{dcases}
\begin{dcases}
E_v(k)=E_v -\frac{\hbar^2 k^2}{2 m_v^*} \\[10pt]
E_c(k)=E_c + \frac{\hbar^2 k^2}{2 m_c^*}
\end{dcases}
Effective mass
"Free" Electrons

E_g
E_f
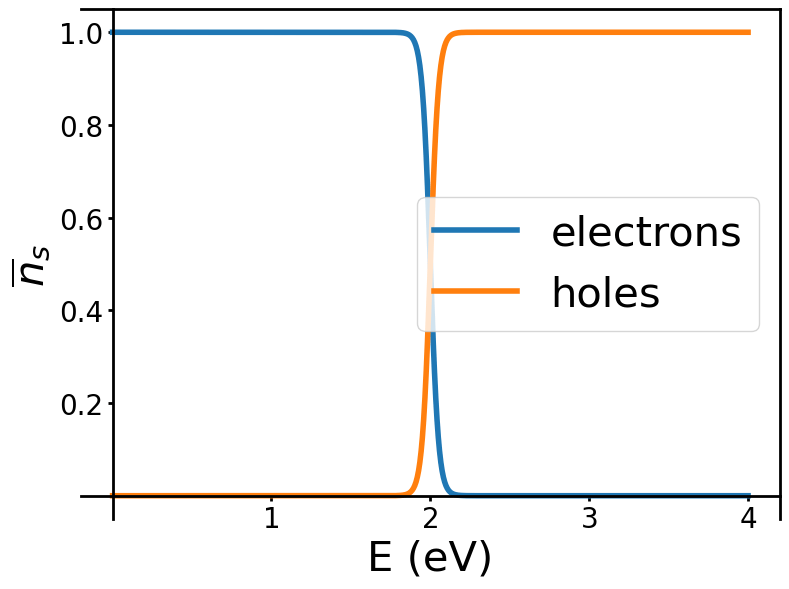
\bar{n}_{s,e} (E) = f_e(E) = \frac{1}{e^{\frac{E-E_{F}}{k_B T}}+1}
WHAT ABOUT THE HOLES?
\begin{align*}
\end{align*}
\begin{align*}
\bar{n}_{s,h} (E) = f_h(E) & = (1-f_e(E)) \\
& = \frac{1}{e^{\frac{E_{F}-E}{k_B T}}+1}
\end{align*}
HOLE - ELECTRON DENSITY AT BOTH BANDS
\begin{align*}
\end{align*}
\begin{aligned}
& n_c(T)=\int_{E_c}^{\infty} g_c(E) f(E) d E=\int_{E_c}^{\infty} g_c(E) \frac{1}{e^{(E-E_f) / k_B T}+1} d E \\[20pt]
& p_v(T)=\int_{-\infty}^{E_v} g_v(E)(1-f(E)) d E=\int_{-\infty}^{E_v} g_v(E)\left(\frac{1}{e^{(E_f-E) / k_B T}+1}\right) d E
\end{aligned}
g_c(E) = \frac{m^*_c}{\hbar^2 \pi^2} \sqrt{\frac{2 m (E-E_c)}{\hbar^2}}
g_v(E) = \frac{m^*_v}{\hbar^2 \pi^2} \sqrt{\frac{2 m (E_v-E)}{\hbar^2}}
NON-DEGENERATE SEMICONDUCTOR APPROXIMATION
\begin{align*}
\end{align*}
\begin{aligned}
& E_c-E_f \gg k_B T \\
& E_f-E_v \gg k_B T
\end{aligned}
\frac{1}{e^{(E-E_f) / k_B T}+1} \approx e^{-(E-E_f) / k_B T}, \, E>E_c
\frac{1}{e^{(E_f-E) / k_B T}+1} \approx e^{-(E_f-E) / k_B T}, E_v>E
HOLE - ELECTRON DENSITY AT BOTH BANDS
\begin{aligned}
& n_c(T)=\int_{E_c}^{\infty} g_c(E) f_e(E) d E \approx(\underbrace{\int_{E_c}^{\infty} g_c(E) e^{-\left(E-E_c\right) / k_B T} d E}_{N_c(T)}) e^{-\left(E_c-E_f\right) /k_B T}=N_c(T) e^{-\left(E_c-E_f\right) /k_B T} \\[50pt]
& p_v(T)=\int_{E_c}^{\infty} g_v(E)(1-f_e(E)) d E \approx(\underbrace{\int_{-\infty}^{E_v} g_v(E) e^{-\left(E_v-E\right) / k_B T} d E}_{P_v(T)}) e^{-\left(E_f-E_v\right) / k_B T}=P_v(T) e^{-\left(E_f-E_v\right) / k_B T}
\end{aligned}
N_c(T) \Rightarrow \text{Effective electron density of states} \\[10pt]
N_p(T) \Rightarrow \text{Effective hole density of states}
EFFECTIVE DENSITIES
\begin{aligned}
& N_c(T)=\int_{E_c}^{\infty} g_c(E) e^{-\left(E-E_c\right) / k_B T} d E=\frac{1}{4}\left(\frac{2 m_c^* k_B T}{\pi \hbar^2}\right)^{3 / 2} \\[20pt]
& P_v(T)=\int_{-\infty}^{E_v} g_v(E) e^{-\left(E_v-E\right) / k_B T} d E=\frac{1}{4}\left(\frac{2 m_v^* k_B T}{\pi \hbar^2}\right)^{3 / 2}
\end{aligned}
LAW OF MASS ACTION
\begin{aligned}
n_c(T) p_v(T) & = N_c(T) P_v(T) e^{\left(E_v-E_c\right)/ k_B T} \\
& = N_c(T) P_v(T) e^{-E_g / k_B T}
\end{aligned}
UNDERSTANDING THE LAW OF MASS ACTION
\begin{aligned}
n_c(T) p_v(T) & = N_c(T) P_v(T) e^{\left(E_v-E_c\right)/ k_B T} \\
& = N_c(T) P_v(T) e^{-E_g / k_B T}
\end{aligned}
The product \(n_c \cdot p_v\) is constant at a fixed temperature and is a function of the band gap
INTRINSIC CARRIER CONCENTRATION
n_c = p_v \equiv n_i
n_i = \sqrt{N_c P_v} e^{-E_g/ 2 k_B T}
E_g(Si) = 1.1 eV \Rightarrow n_i \approx 10^{10} \, cm^{-3}
E_g(Ge) = 0.67 eV \Rightarrow n_i \approx 2 \cdot 10^{13} \, cm^{-3}
COMPUTING THE FERMI ENERGY \(E_f\)
n_c=N_c e^{-\frac{\left(E_c-E_f\right)}{k_B T}}=n_i=\sqrt{P_v N_c} e^{-\frac{E_g}{2 K_B T}}
e^{\frac{E_f-E_c+E_g / 2}{k_B T}}=\sqrt{\frac{P_v}{N_c}}=\left(\frac{m_v^*}{m_c^{*}}\right)^{3 / 4}
E_f=\frac{E_v+E_c}{2} + \frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)
E_f=E_v+\frac{1}{2} E_g+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)
E_f=E_c-\frac{1}{2} E_g+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right) \\
CHARGE TRANSPORT, CONDUCTIVITY AND MOBILITY:1
\begin{dcases}
\vec{F}=-e \vec{E} \\
\vec{F}=m \frac{d \vec{v}}{d t}
\end{dcases}
\Rightarrow
m \frac{d \vec{v}}{d t}=-e \vec{E} \Rightarrow \vec{v}(t)=-\frac{e E}{m} t
\begin{dcases}
\vec{j}=n \cdot q \cdot \vec{v}, \text { where } n=\frac{N}{V} \\
\vec{v}=-\frac{e E}{m} t
\end{dcases}
\Rightarrow
\begin{dcases}
\vec{j}=n \cdot e \cdot \vec{v}=\sigma \vec{E} \\
\sigma=\frac{n e^2 t}{m}
\end{dcases}
\vec{v}=-\frac{e E \tau}{m}
\Rightarrow
\sigma=\frac{n e^2 \tau}{m}
CHARGE TRANSPORT, CONDUCTIVITY AND MOBILITY:2
\sigma=\frac{n_c e^2 \tau_n}{m^*_c} + \frac{p_v e^2 \tau_p}{m^*_v}
In the case of semiconductor, conductivity has two kinds of carriers (electrons and holes) and both contributes to the conductivity
\sigma=n_c e \mu_n + p_v e \mu_p \, \text{ with } \,
\begin{dcases}
\mu_n = \frac{e \tau_n}{m^*_c}\\[10pt]
\mu_p = \frac{e \tau_p}{m^*_v}
\end{dcases}
\text{ mobilities for electrons and holes}
CHARGE TRANSPORT, CONDUCTIVITY AND MOBILITY:3
\sigma=n_c e \mu_n + p_v e \mu_p \, \text{ with } \,
\begin{dcases}
\mu_n = \frac{e \tau_n}{m^*_c}\\[10pt]
\mu_p = \frac{e \tau_p}{m^*_v}
\end{dcases}
\text{ mobilities for electrons and holes}
ARRANGEMENTS OF ATOMS: 1D
a
x
1D Lattice: \(\{\vec{R}\}, \, \vec{R}=ma, \, m \in \mathbb{Z}\)
-\frac{a}{2}
\frac{a}{2}
Wigner-Seitz Cell
a
Primitive Cell
ARRANGEMENTS OF ATOMS: 2D
Wigner-Seitz Cell
Primitive Cell
Rectangular
Square
Centered Rectangular
Oblique
Hexagonal

Voronoi Tesselation
3D ARRANGEMENTS OF ATOMS: BRAVAIS LATTICE
3D ARRANGEMENTS OF ATOMS: Wigner-Seitz Cell

ENGINEERING CARRIER CONCENTRATIONS


II
VI
III
IV
V
\text{Si}: \, 1 s^2 2 s^2 2 p^6 3 s^2 3 p^2
3 s 3 p
sp3
\text{Si}: \, 1 s^2 2 s^2 2 p^6 3 s^2 3 p^2



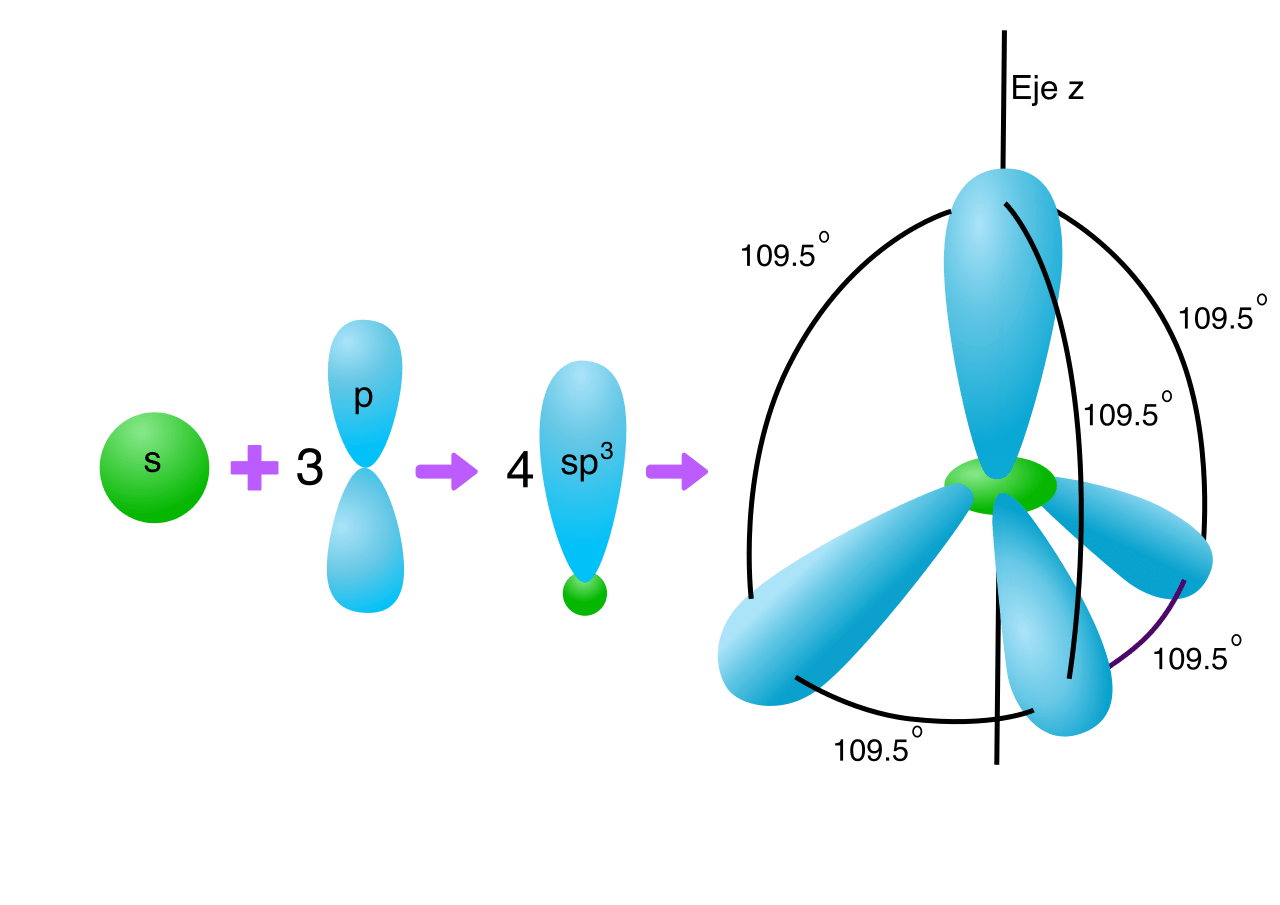
N-TYPE DOPING: PHOSPHORUS


II
VI
III
IV
V

\text{P}: \, 1 s^2 2 s^2 2 p^6 3 s^2 3 p^3
3 s 3 p
\text{P}: \, 1 s^2 2 s^2 2 p^6 3 s^2 3 p^3
sp3
P-TYPE DOPING: BORON


II
VI
III
IV
V
\text{B}: \, 1 s^2 2 s^2 2 p^1
2 s 2 p
sp2
\text{B}: \, 1 s^2 2 s^2 2 p^1
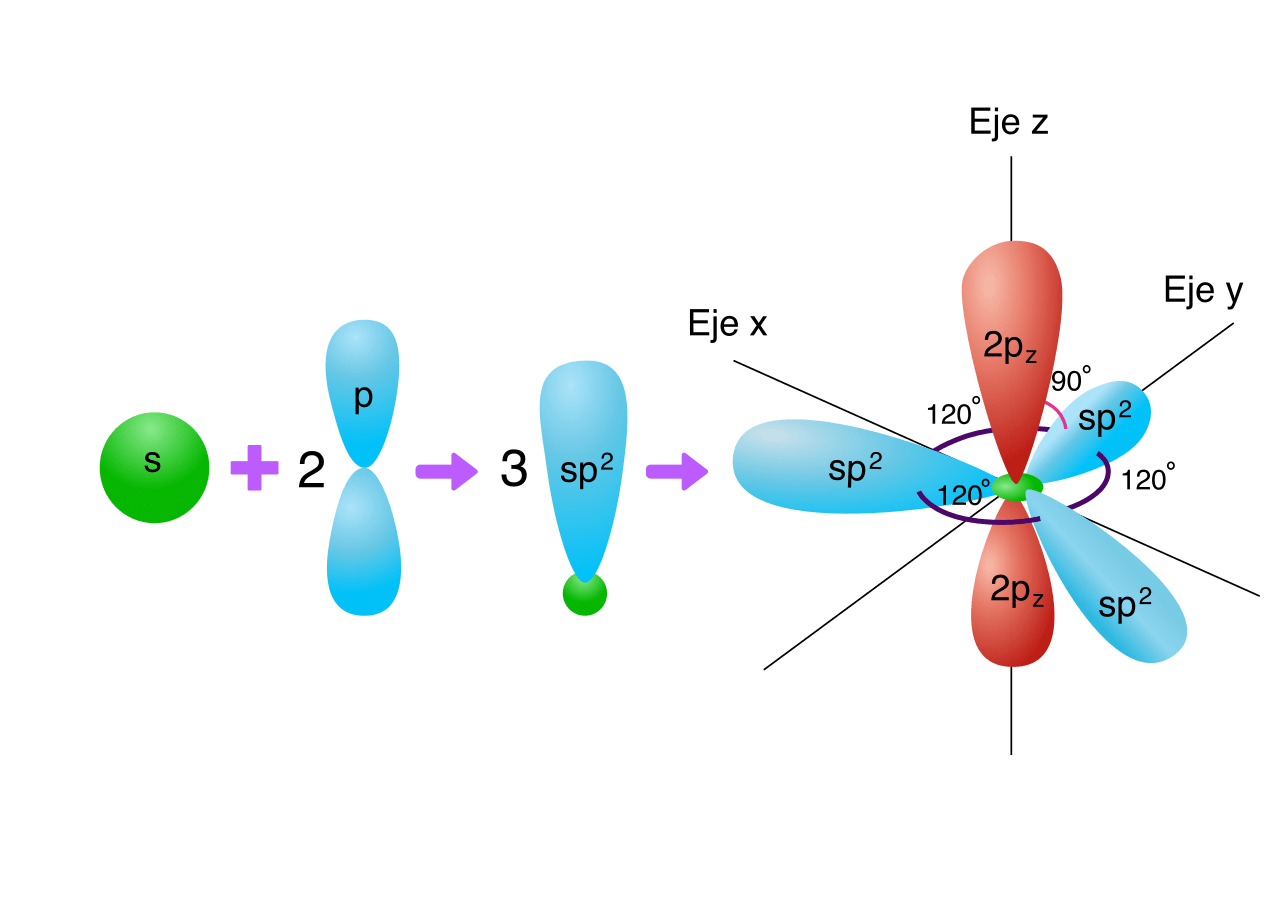
N-TYPE AND P-TYPE DOPING
\text{P}: \, 1 s^2 2 s^2 2 p^6 3 s^2 3 p^3
sp3
sp2
\text{B}: \, 1 s^2 2 s^2 2 p^1
x
E
E_F
E_a
Acceptor Levels
x
E
E_F
E_d
Donor Levels
DEEP TRAPS: GOLD IMPURITIES


x
E
E_F
\text{deep trap}
HOW MUCH DOPING DO WE NEED FOR SILICON?
N-Type Doping
P-Type Doping
n_i^2=N_e P_v e^{-\frac{E_g}{k_B T}} \sim 10^{20} \mathrm{~cm}^{-6} \Rightarrow n_i \sim 10^{10} \mathrm{~cm}^{-3}
We replace one atom every million: \( \text{1 ppm} \)
\begin{dcases}
n_{Si} \sim 10^{22} \mathrm{~cm}^{-3} \\
N_{D} \sim 10^{16} \mathrm{~cm}^{-3} \\
\end{dcases} \\
\Downarrow \\
n_c = n_i + N_D \sim N_D \sim 10^{16} \mathrm{~cm}^{-3} \\
\Downarrow \\
p_v = \frac{n_i^2}{n_c} \sim 10^{4} \mathrm{~cm}^{-3} \\
\begin{dcases}
n_{Si} \sim 10^{22} \mathrm{~cm}^{-3} \\
N_{A} \sim 10^{16} \mathrm{~cm}^{-3} \\
\end{dcases} \\
\Downarrow \\
p_v = n_i + N_A \sim N_A \sim 10^{16} \mathrm{~cm}^{-3} \\
\Downarrow \\
n_c = \frac{n_i^2}{p_v} \sim 10^{4} \mathrm{~cm}^{-3} \\
EFFECT OF DOPING ON THE CONDUCTIVITY
N-Type Doping
P-Type Doping
\sigma_i=\frac{n_c e^2 \tau_n}{m^*_c} + \frac{p_v e^2 \tau_p}{m^*_v}
\sigma \sim \sigma_D = \frac{N_D e^2 \tau_n}{m^*_c} \sim 10^6 \sigma_i
The conductivity is dominated by the electron provided by the donor atoms
\sigma_i=\frac{n_c e^2 \tau_n}{m^*_c} + \frac{p_v e^2 \tau_p}{m^*_v}
\sigma \sim \sigma_A = \frac{N_A e^2 \tau_p}{m^*_v} \sim 10^6 \sigma_i
The conductivity is dominated by the holes provided by the acceptor atoms
EFFECT OF DOPING OVER THE FERMI LEVEL
\begin{aligned}
n_c \approx N_D &, p_v \approx \frac{n_i^2}{N_D} \\
&\Downarrow \\
P_v e^{\left(E_v-E_f\right) / k_B T}=\frac{n_i^2}{N_D}&=n_i \frac{n_i}{N_D}=\sqrt{P_v N_c} e^{-E_g / 2 k_B T} \frac{n_i}{N_D} \\
& \Downarrow \\
e^{\left(E_f-E_v-\frac{E_g}{2}\right) / k_B T}&=\sqrt{\frac{P_v}{N_c}} \frac{N_D}{n_i} \\
& \Downarrow \\
e^{\left(E_f-E_v-\frac{E_g}{2}\right) / k_B T}&=\left(\frac{m_v^*}{m_c^*}\right)^{\frac{3}{4}} \frac{N_D}{n_i} \\
& \Downarrow \\
\end{aligned}
EFFECT OF DOPING OVER THE FERMI LEVEL
E_f=E_v+\frac{E_g}{2}+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)+k_B T \ln \left(\frac{N_D}{n_i}\right)=E_{f,i}+k_B T \ln \left(\frac{N_D}{n_i}\right)
E_f=E_v+\frac{E_g}{2}+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)-k_B T \ln \left(\frac{N_A}{n_i}\right)=E_{f,i}-k_B T \ln \left(\frac{N_A}{n_i}\right)
N-Type Doping
P-Type Doping
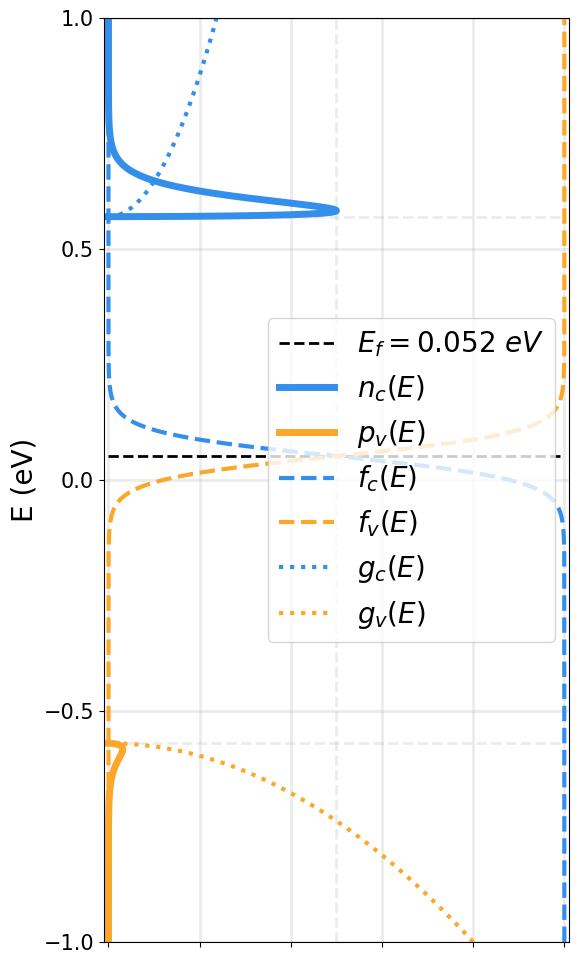
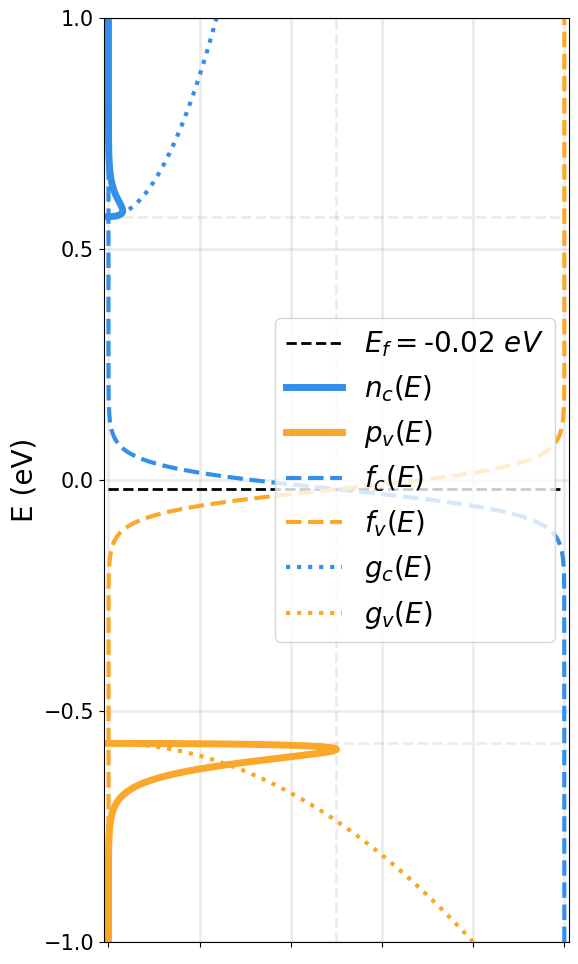
EFFECT OF DOPING OVER THE FERMI LEVEL
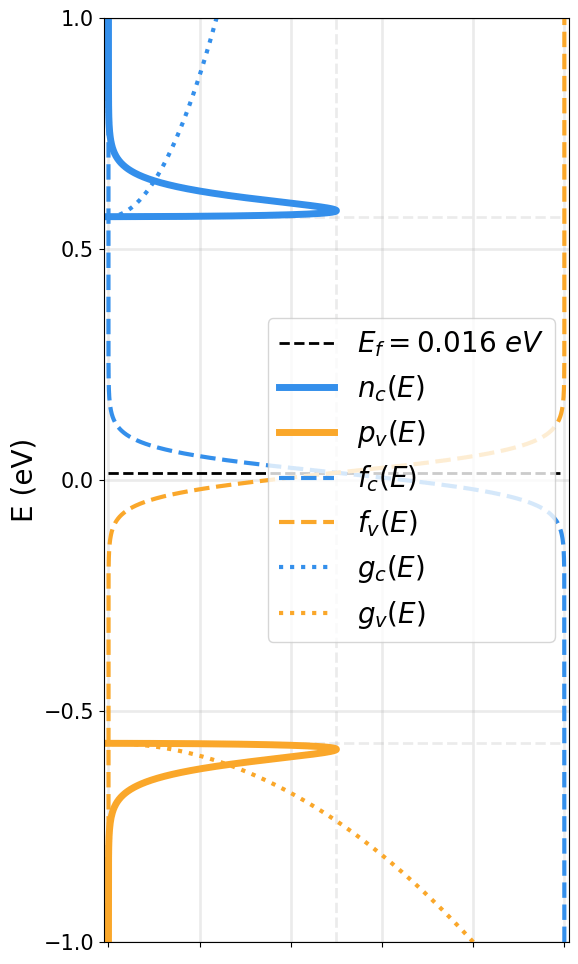
N-Type
Intrinsic
P-Type
Materials and Platforms for AI - Band Structure: Density of States
By Giovanni Pellegrini
Materials and Platforms for AI - Band Structure: Density of States
- 147



