P-N Junctions
DOPED SEMICONDUCTORS
THE EFFECT OF TEMPERATURE
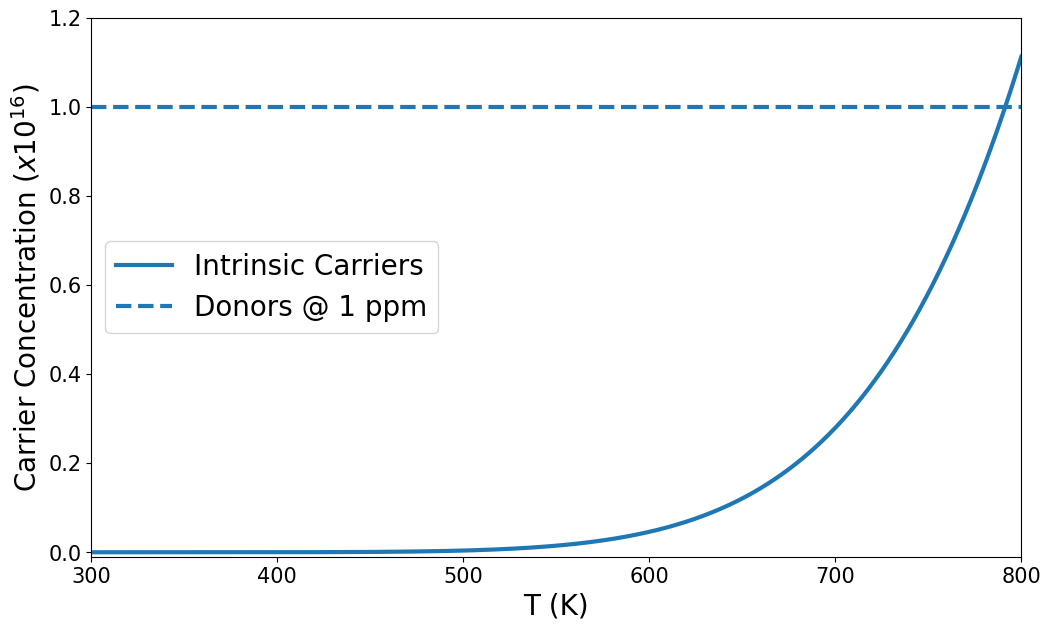
DOPED SEMICONDUCTORS
THE EFFECT OF TEMPERATURE
x
E
E_F
E_d
T=0K
x
E
E_F
E_d
T=300K
x
E
E_F
E_d
T=1000K
P-N JUNCTIONS AT EQUILIBRIUM
P-Type Semiconductor: \(N_A\)
N-Type Semiconductor: \(N_D\)
P-N JUNCTIONS: DEPLETION REGION
P-Type Semiconductor
N-Type Semiconductor
x_p
x_n
Depletion Region: \(x_0\)
P-N JUNCTIONS: BUILT-IN FIELD
P-Type Semiconductor
N-Type Semiconductor
x_p
x_n
Depletion Region: \(x_0\)
\vec{E}
P-N JUNCTIONS: COMPUTING THE FIELD
\rho(x)
x
x_p
x_n
\rho_n = e N_D
\rho_p = -e N_A
\rho(x)=
\begin{dcases}
-e N_A, \, -x_{p} < x < 0 \\
e N_D, \, 0 < x < x_{n}
\end{dcases}
\frac{x_p}{x_n} = \frac{N_D}{N_A} \Rightarrow N_A x_p = N_D x_n
Charge Distribution
Gauss Law
\begin{dcases}
\oint \vec{E} \cdot d\vec{S} = \frac{Q}{\varepsilon_{s}\varepsilon_{0}} \\[10pt]
\vec{\nabla} \cdot \vec{E} = \frac{\rho(\vec{r})}{\varepsilon_{s}{\varepsilon_{0}}}
\end{dcases}
\Rightarrow
\frac{dE}{dx} = \frac{\rho(x)}{\varepsilon_{s}{\varepsilon_{0}}}
P-N JUNCTIONS: COMPUTING THE FIELD
\rho(x)
x
x_p
x_n
P-Type Field
\begin{dcases}
\int_{-x_p}^x \frac{dE}{dx}dx = E(x) - E(-x_p) \\[10pt]
\int_{-x_p}^x -\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}dx = -\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p) \\[10pt]
E(-x_p) = 0
\end{dcases} \\
\Downarrow \\
E(x) = -\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p)
\rho_n = e N_D
\rho_p = -e N_A
P-N JUNCTIONS: COMPUTING THE FIELD
N-Type Field
\begin{dcases}
\int_{x}^{x_n} \frac{dE}{dx}dx = E(x_n) - E(x) \\[10pt]
\int_{x}^{x_n} +\frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}dx = \frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x_n-x) \\[10pt]
E(x_n) = 0
\end{dcases} \\
\Downarrow \\
E(x) = \frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x-x_n)
\rho(x)
x
x_p
x_n
\rho_n = e N_D
\rho_p = -e N_A
P-N JUNCTIONS: COMPUTING THE FIELD
E(x)
x
x_p
x_n
Total Field
E(x) =
\begin{dcases}
-\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p) \text{, P-Type} \\[10pt]
\frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x-x_n) \text{, N-Type}
\end{dcases}
E_{max}
E_{\max }=-\frac{e N_A x_p}{\varepsilon_{s}\varepsilon_{0}}=-\frac{e N_D x_n}{\varepsilon_{s}\varepsilon_{0}}
P-N JUNCTIONS: BUILT-IN VOLTAGE
E(x)
x
x_p
x_n
E(x) =
\begin{dcases}
-\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p) \text{, P-Type} \\[10pt]
\frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x-x_n) \text{, N-Type}
\end{dcases}
V(x)=-\int_{-x_p}^x E\left(x^{\prime}\right) d x' \\
\Downarrow \\
\begin{aligned}
V(x) & = -\left(-\frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}(x+x_p) \cdot (x+x_p)\right) \\
V(x) & = \frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}(x+x_p)^2
\end{aligned}
x
P-Type
P-N JUNCTIONS: BUILT-IN VOLTAGE
E(x)
x
x_p
x_n
E(x) =
\begin{dcases}
-\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p) \text{, P-Type} \\[10pt]
\frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x-x_n) \text{, N-Type}
\end{dcases}
V(x)=-\int_{0}^x E\left(x^{\prime}\right) d x \\
\Downarrow \\
\begin{aligned}
V(x) & = \frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}x_p^2 +
(\frac{e N_D x_n}{\varepsilon_{s}\varepsilon_{0}} + \frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x_n-x)) \cdot \frac{x}{2}\\
V(x) & = \frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}x_p^2 +\frac{e N_D}{2\varepsilon_{s}\varepsilon_{0}}(2 x_n x -x^2)\\
V(x) & = \frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}x_p^2 + \frac{eN_D}{2\varepsilon_{s}\varepsilon_{0}}x_n^2
- \frac{e N_D}{2\varepsilon_{s}\varepsilon_{0}}(x-x_n)^2\\
\end{aligned}
x
N-Type
P-N JUNCTIONS: BUILT-IN VOLTAGE
V(x) =
\begin{dcases}
\frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}(x+x_p)^2 \text{, P-Type} \\[10pt]
\frac{e}{2\varepsilon_{s}\varepsilon_{0}}(N_A x_p^2 + N_D x_n^2) - \frac{e N_D}{2\varepsilon_{s}\varepsilon_{0}}(x-x_n)^2 \text{, N-Type}
\end{dcases}\\
\Downarrow \\
V\left(x_n\right)=V_0=\frac{e}{2 \varepsilon_{s}\varepsilon_{0}}\left(N_A x_p^2+N_D x_n^2\right)
\begin{dcases}
x_p+x_n=x_0 \\
x_p N_A=x_n N_D \\
\end{dcases}
\Rightarrow
\begin{dcases}
x_p=\frac{x_0}{1+\frac{N_A}{N_D}}\\
x_n=\frac{x_0}{1+\frac{N_D}{N_A}}
\end{dcases}\\
\Downarrow\\
V_0=\frac{e}{2 \varepsilon_{s}\varepsilon_{0}} x_0^2 \frac{N_A N_D}{N_A + N_D}
P-N JUNCTIONS: DEPLETION WIDTH
V_0=\frac{e}{2 \varepsilon_{s}\varepsilon_{0}} x_0^2 \frac{N_A N_D}{N_A + N_D}\\[5pt]
\Downarrow \\[5pt]
x_0=\sqrt{\frac{2 \varepsilon_{s}\varepsilon_{0} V_0}{e}\frac{N_A+N_D}{N_A N_D}}\\[5pt]
\Downarrow \\[5pt]
x_n=\sqrt{\frac{2 \varepsilon_{s} \varepsilon_0 V_{0}}{e} \frac{N_A}{N_D\left(N_A+N_D\right)}}
x_p=\sqrt{\frac{2 \varepsilon_{s} \varepsilon_0 V_{0}}{e} \frac{N_D}{N_A\left(N_A+N_D\right)}}
BUILT IN VOLTAGE \(V_0\): FERMI LEVELS
E_{f,n}=E_v+\frac{E_g}{2}+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)+k_B T \ln \left(\frac{N_D}{n_i}\right)=E_{f,i}+k_B T \ln \left(\frac{N_D}{n_i}\right)
E_{f,p}=E_v+\frac{E_g}{2}+\frac{3}{4} k_B T \ln \left(\frac{m_v^*}{m_c^*}\right)-k_B T \ln \left(\frac{N_A}{n_i}\right)=E_{f,i}-k_B T \ln \left(\frac{N_A}{n_i}\right)
N-Type Doping
P-Type Doping
BUILT IN VOLTAGE \(V_0\): FERMI LEVELS
x
E
E_{f,p}
P-Type
\Delta E = E_{f,n} -E_{f,p}
x
E
E_{f,n}
N-Type
BUILT IN VOLTAGE \(V_0\): FERMI LEVELS
eV_0 = E_{f,n} -E_{f,p}
E_n
P-Type
E_{f}
N-Type
x
E_p
BUILT IN VOLTAGE \(V_0\): FERMI LEVELS
\begin{dcases}
E_{f,n}=E_{f,i}+k_B T \ln \left(\frac{N_D}{n_i}\right) \\[10pt]
E_{f,p}=E_{f,i}-k_B T \ln \left(\frac{N_A}{n_i}\right)
\end{dcases}\\[5pt]
\Downarrow \\[5pt]
V_{0}=\frac{k_B T}{e} \ln \left(\frac{N_A N_D}{n_i^2}\right)
BUILT IN VOLTAGE \(V_0\): FERMI LEVELS
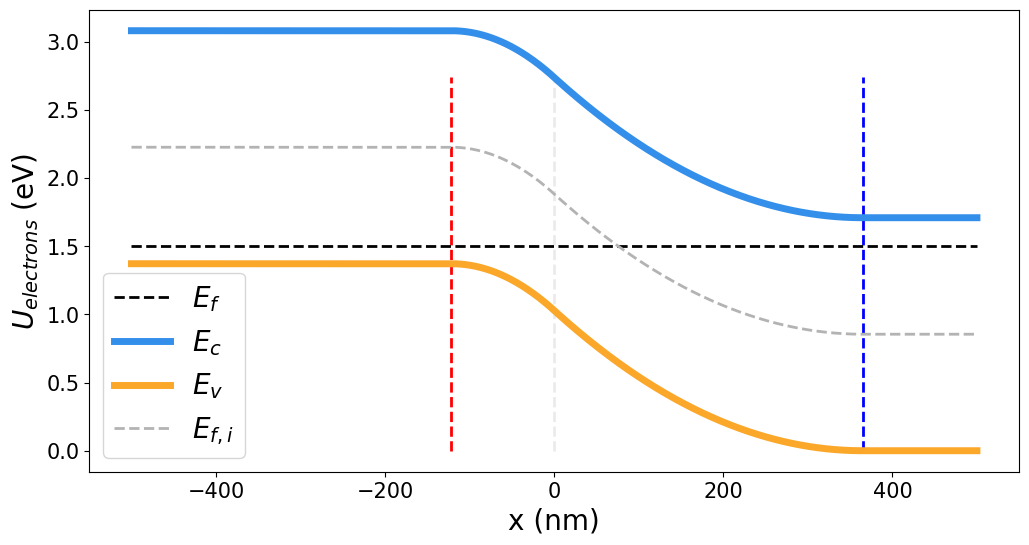
P-N JUNCTIONS: EQUILIBRIUM
\(p_{p0} \simeq N_A\): Majority Carriers \(\Rightarrow\) Diffusion
\(n_{p0} \simeq \frac{n_i^2}{N_A}\): Minority Carriers \(\Rightarrow\) Drift
P-Type Semiconductor
N-Type Semiconductor
\vec{E}
\(n_{n0} \simeq N_D\): Majority Carriers \(\Rightarrow\) Diffusion
\(p_{n0} \simeq \frac{n_i^2}{N_D}\): Minority Carriers \(\Rightarrow\) Drift
P-N JUNCTIONS: DEPLETION WIDTH
V_0=\frac{e}{2 \varepsilon_{s}\varepsilon_{0}} x_0^2 \frac{N_A N_D}{N_A + N_D}\\[5pt]
\Downarrow \\[5pt]
x_0=\sqrt{\frac{2 \varepsilon_{s}\varepsilon_{0} V_0}{e}\frac{N_A+N_D}{N_A N_D}}\\[5pt]
\Downarrow \\[5pt]
x_n=\sqrt{\frac{2 \varepsilon_{s} \varepsilon_0 V_{0}}{e} \frac{N_A}{N_D\left(N_A+N_D\right)}}
x_p=\sqrt{\frac{2 \varepsilon_{s} \varepsilon_0 V_{0}}{e} \frac{N_D}{N_A\left(N_A+N_D\right)}}
P-N JUNCTIONS: DEPLETION CHARGE DENSITY
\rho(x)=
\begin{dcases}
-e N_A, \, -x_{p} < x < 0 \\
e N_D, \, 0 < x < x_{n}
\end{dcases}
P-N JUNCTIONS: DEPLETION CHARGE DENSITY
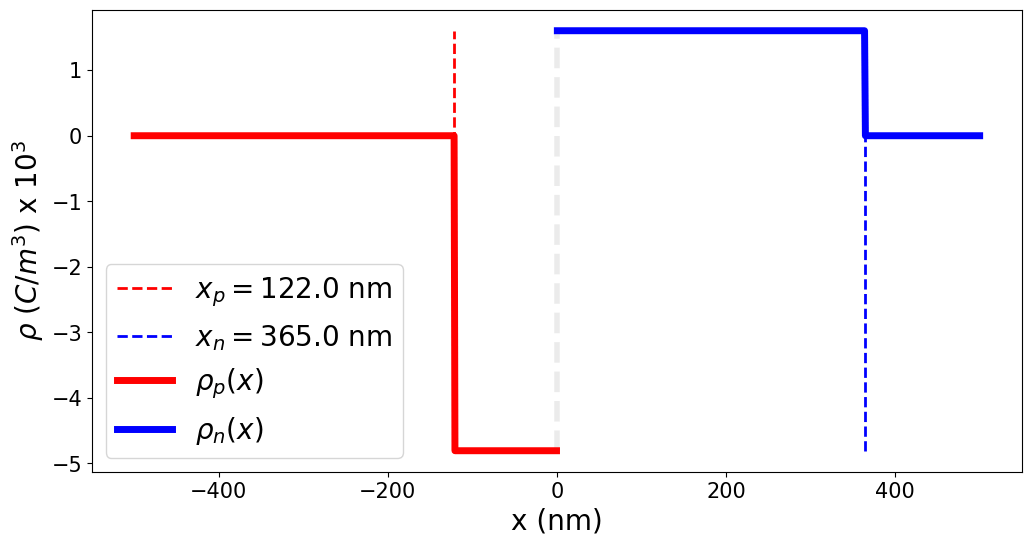
P-Type
N-Type
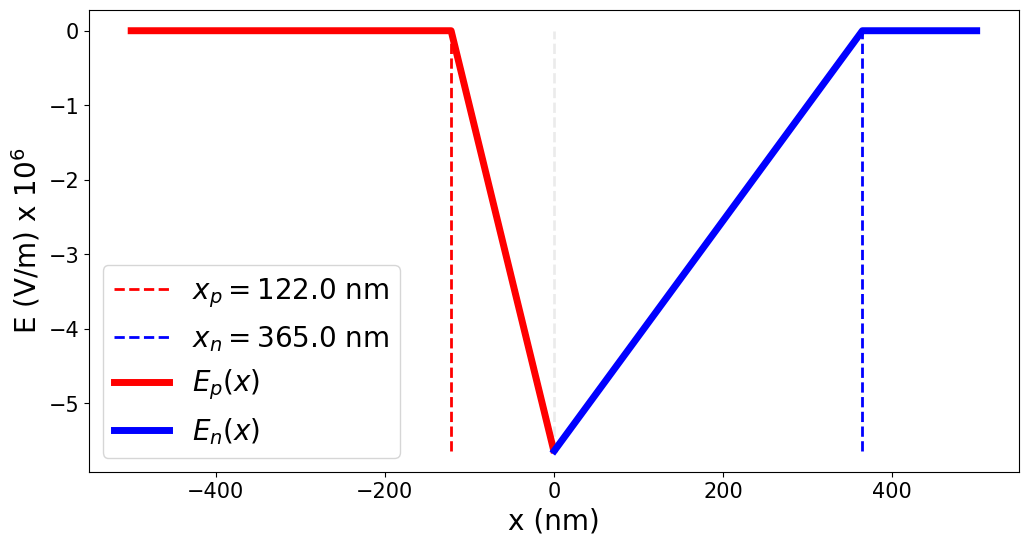
P-N JUNCTIONS: BUILT-IN FIELDS
E(x) =
\begin{dcases}
-\frac{eN_A}{\varepsilon_{s}\varepsilon_{0}}(x+x_p) \text{, P-Type} \\[10pt]
\frac{e N_D}{\varepsilon_{s}\varepsilon_{0}}(x-x_n) \text{, N-Type}
\end{dcases}
P-N JUNCTIONS: BUILT-IN FIELDS
P-Type
N-Type
P-N JUNCTIONS: BUILT-IN VOLTAGE
V(x) =
\begin{dcases}
\frac{eN_A}{2\varepsilon_{s}\varepsilon_{0}}(x+x_p)^2 \text{, P-Type} \\[10pt]
\frac{e}{2\varepsilon_{s}\varepsilon_{0}}(N_A x_p^2 + N_D x_n^2) - \frac{e N_D}{2\varepsilon_{s}\varepsilon_{0}}(x-x_n)^2 \text{, N-Type}
\end{dcases}\\
P-N JUNCTIONS: BUILT-IN VOLTAGE
P-Type
N-Type
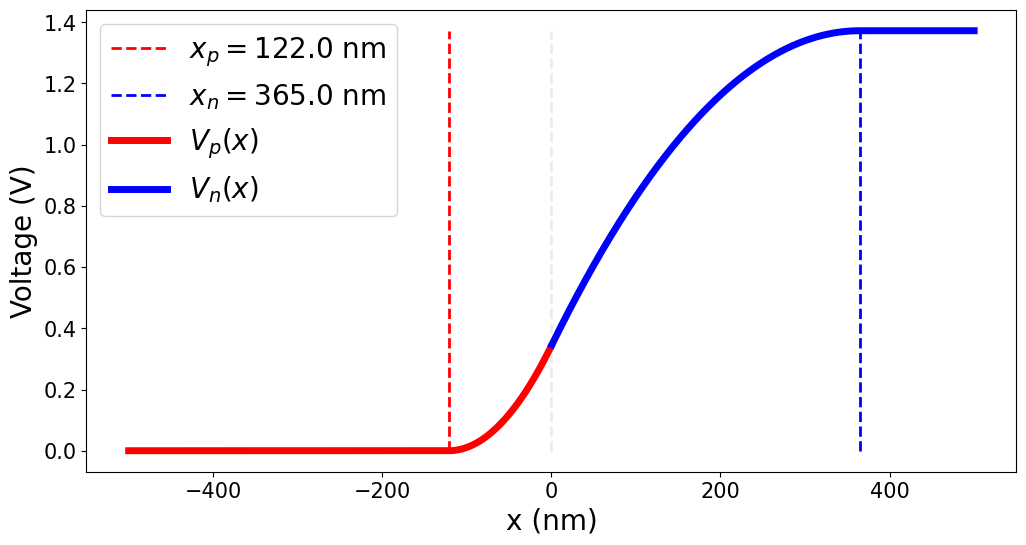
P-N JUNCTIONS: HOLES POTENTIAL ENERGY
P-Type
N-Type
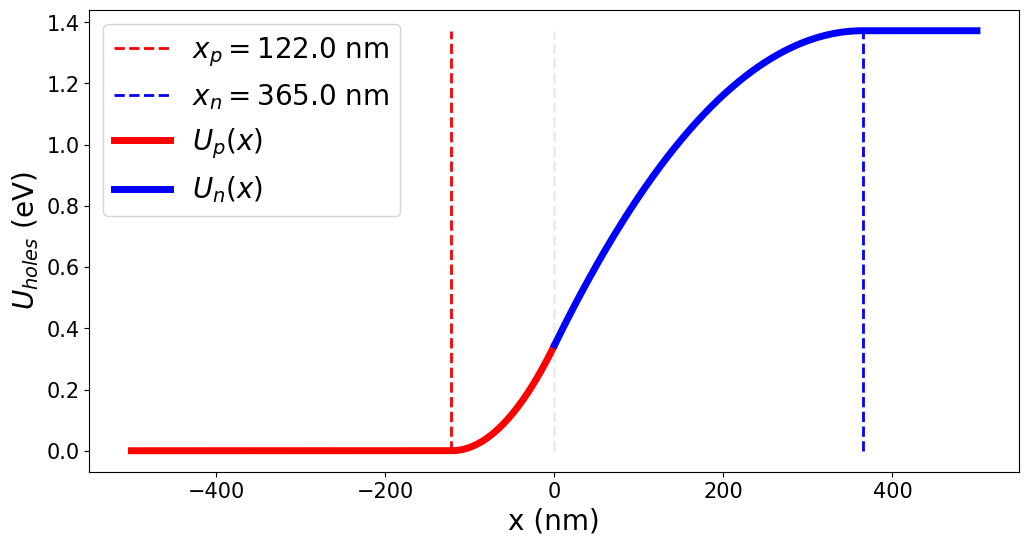
P-N JUNCTIONS: ELECTRONS POTENTIAL ENERGY
P-Type
N-Type
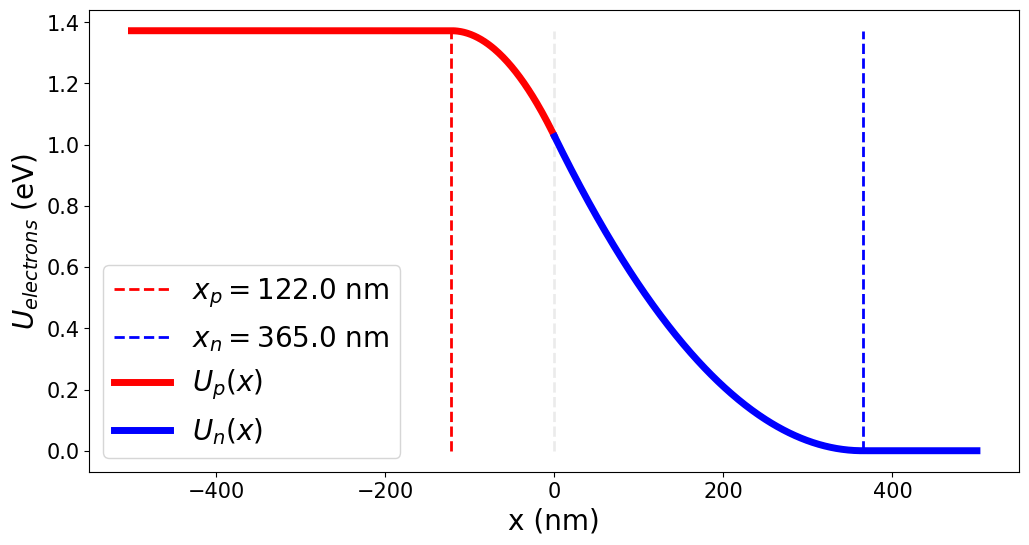
P-N JUNCTIONS: CARRIER CONCENTRATION
P-Type
N-Type
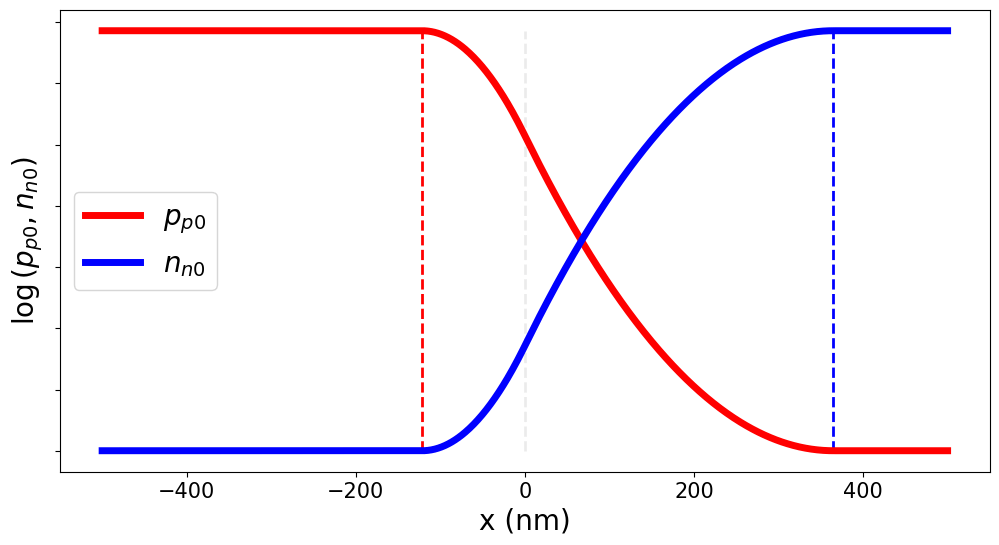
P-N JUNCTIONS: OUT OF EQUILIBRIUM
\(p_{p0} \simeq N_A\): Majority Carriers \(\Rightarrow\) Diffusion
\(n_{p0} \simeq \frac{n_i^2}{N_A}\): Minority Carriers \(\Rightarrow\) Drift
P-Type Semiconductor
N-Type Semiconductor
\vec{E}
\(n_{n0} \simeq N_D\): Majority Carriers \(\Rightarrow\) Diffusion
\(p_{n0} \simeq \frac{n_i^2}{N_D}\): Minority Carriers \(\Rightarrow\) Drift
P-N JUNCTIONS: OUT OF EQUILIBRIUM
\(p_{p0} \simeq N_A\): Majority Carriers \(\Rightarrow\) Diffusion
\(n_{p0} \simeq \frac{n_i^2}{N_A}\): Minority Carriers \(\Rightarrow\) Drift
\(n_{n0} \simeq N_D\): Majority Carriers \(\Rightarrow\) Diffusion
\(p_{n0} \simeq \frac{n_i^2}{N_D}\): Minority Carriers \(\Rightarrow\) Drift
\Downarrow \\[5pt]
V_{0}=\frac{k_B T}{e} \ln \left(\frac{N_A N_D}{n_i^2}\right) = \frac{k_B T}{e} \ln \left(\frac{n_{n0}}{n_{p0}}\right)
= \frac{k_B T}{e} \ln \left(\frac{p_{p0}}{p_{n0}}\right)\\[5pt]
\Downarrow \\[5pt]
\begin{dcases}
n_{p0} = n_{n0} e^{\frac{-e V_0}{k_B T}} \\[10pt]
p_{n0} = p_{p0} e^{\frac{-e V_0}{k_B T}} \\[10pt]
\end{dcases}
P-N JUNCTIONS: CARRIER CONCENTRATION
P-Type
N-Type

\vec{E}
P-N JUNCTIONS: CARRIER CONCENTRATION

P-N JUNCTIONS: DIFFUSION CURRENT
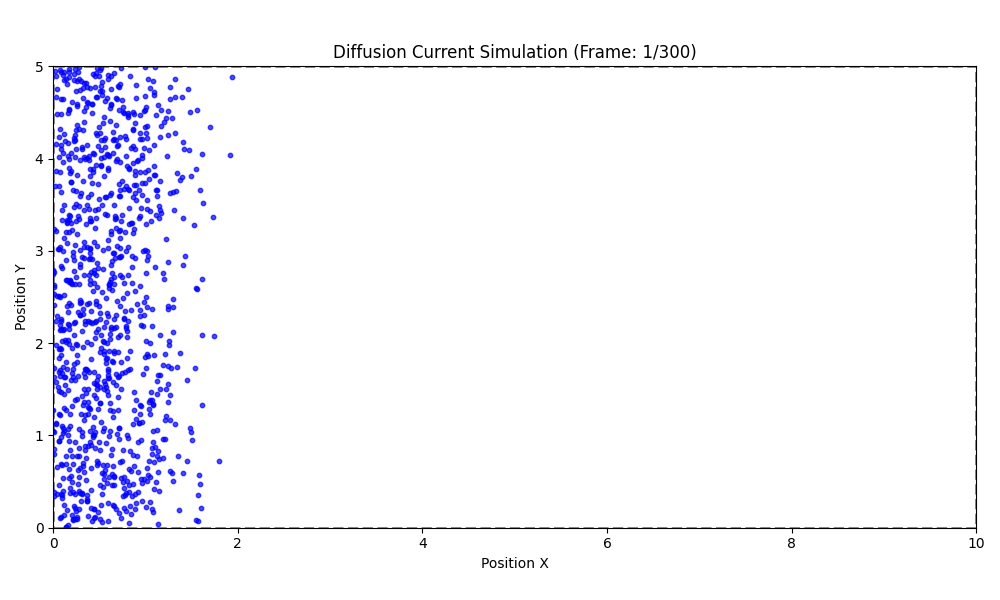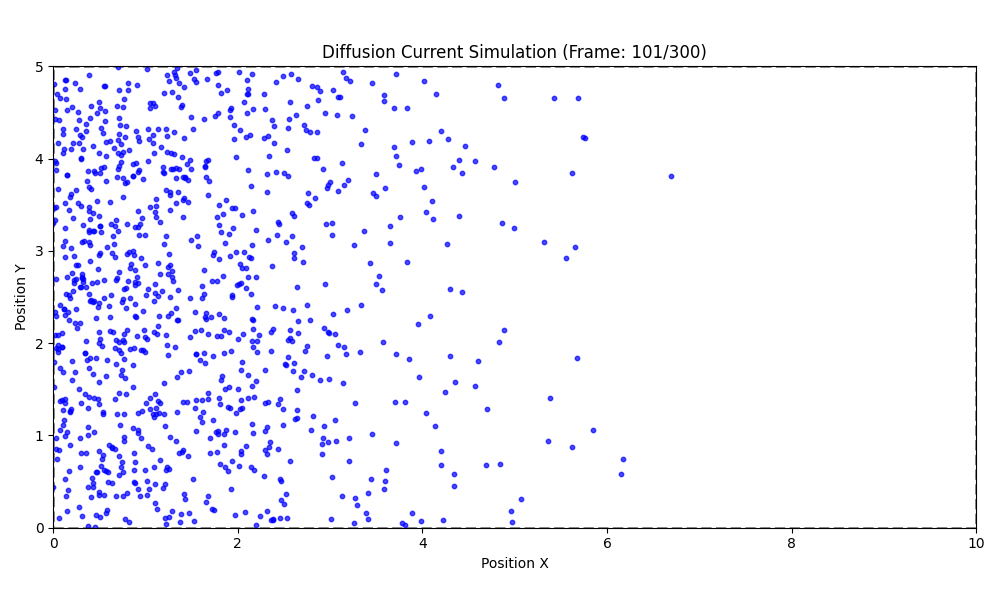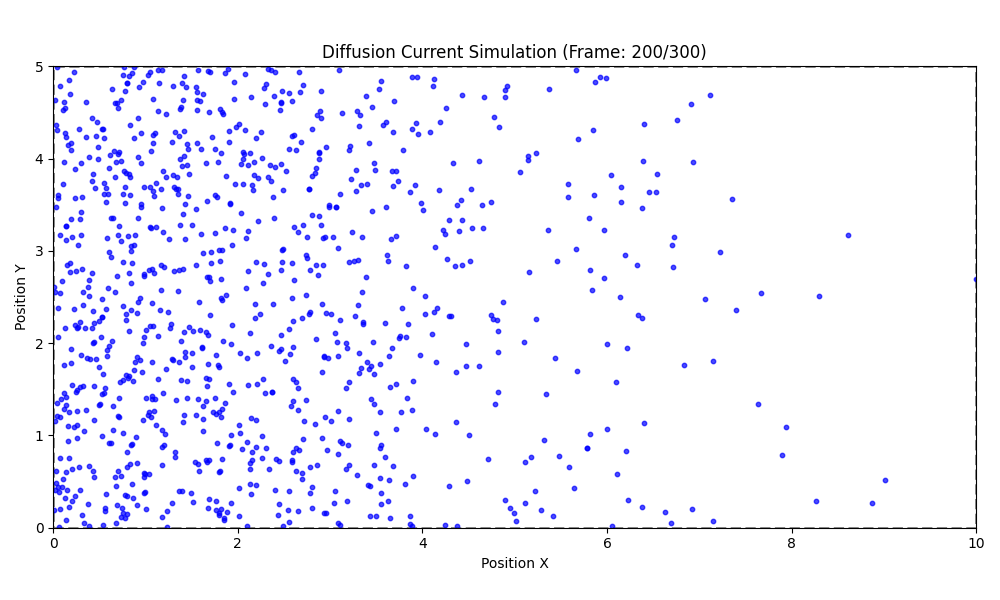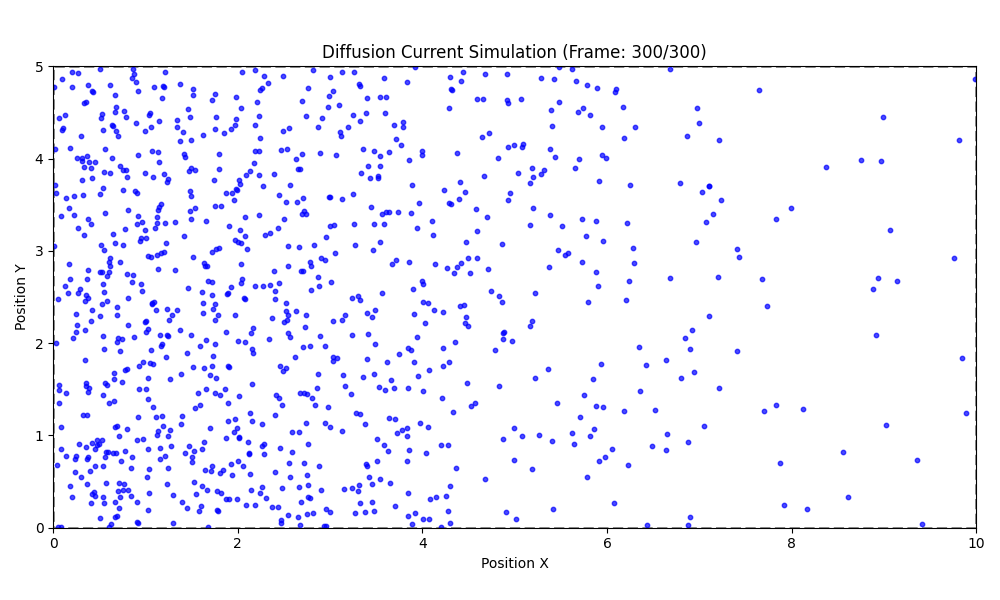
P-N JUNCTIONS: DIFFUSION CURRENT
x
p(x)
x
n(x)
J_{D,p}=-e D_p \frac{d p(x)}{d x}
J_{D,n}=e D_n \frac{d n(x)}{d x}
P-N JUNCTIONS: DRIFT CURRENT
\begin{aligned}
\vec{j}_{drift}=n \cdot e \cdot \vec{v}=\sigma \vec{E} \\
\end{aligned}\\
\Downarrow
\sigma=n_c e \mu_n + p_v e \mu_p \, \text{ with } \,
\begin{dcases}
\mu_n = \frac{e \tau_n}{m^*_c}\\[10pt]
\mu_p = \frac{e \tau_p}{m^*_v}
\end{dcases}
\text{, }
\begin{dcases}
v_{d,n} = \mu_n E\\[10pt]
v_{d,p} = \mu_p E
\end{dcases}\\
\Downarrow
j_{drift} = j_{drift,n} + j_{drift,p} = n_c e \mu_n E + p_v e \mu_p E
CURRENT EQUILIBRIUM: EINSTEN RELATIONS
\begin{dcases}
j_{D,p} + j_{drift,p} = -e D_p \frac{d p(x)}{d x} + p(x) e \mu_p E = 0 \\[10pt]
j_{D,n} + j_{drift,n} = e D_n \frac{d n(x)}{d x} + n(x) e \mu_n E = 0 \\
\end{dcases}\\
\Downarrow\\
\begin{dcases}
D_p=\frac{k_B T \mu_p}{e} \\[10pt]
D_n=\frac{k_B T \mu_n}{e}
\end{dcases}
WHAT ARE THE CONCENTRATION PROFILES \(p(x)\)AND \(n(x)\)?
STEADY STATE INJECTION OF MINORITY CARRIERS
n_{p0}
/cuscini-oblunghi-minion-kevin.jpg.jpg)
\Delta n
\begin{dcases}
p_n(x)=p_n(0) \exp \left(-\frac{x}{L_p}\right);\, \Delta p_n(x)= \Delta p_n(0) \exp \left(-\frac{x}{L_p}\right)\\
n_p(x)=n_p(0) \exp \left(-\frac{x}{L_n}\right); \, \Delta n_p(x)= \Delta n_p(0) \exp \left(-\frac{x}{L_n}\right)
\end{dcases}
L_p=\sqrt{D_p \tau_p}\\
L_n=\sqrt{D_n \tau_n} \\
L_{p,n} \rightarrow \text{Diffusion length} \\
D_{p,n} \rightarrow \text{Diffusion coefficient} \\
\tau_{p,n} \rightarrow \text{Recombination time}
P-Type
P-N JUNCTIONS: FORWARD BIAS
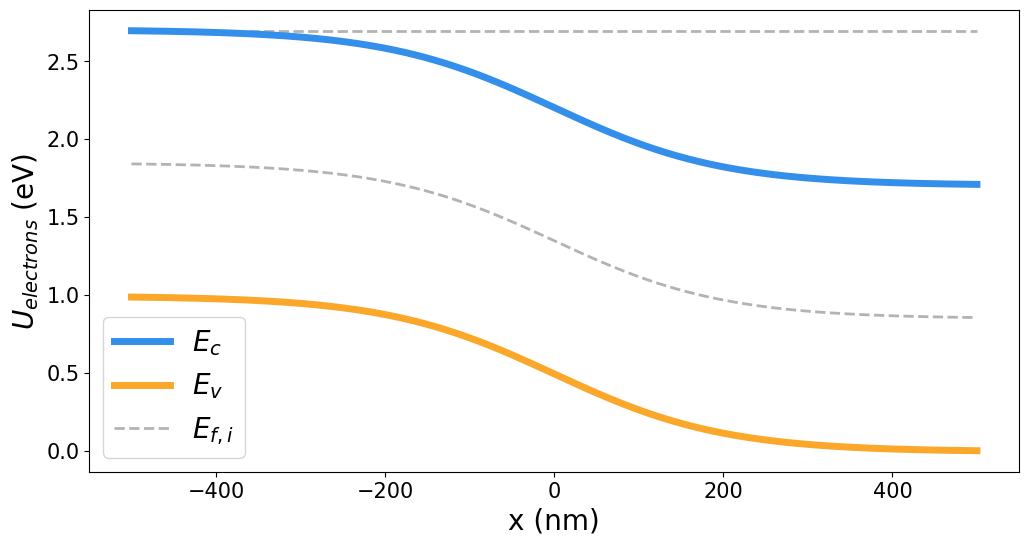
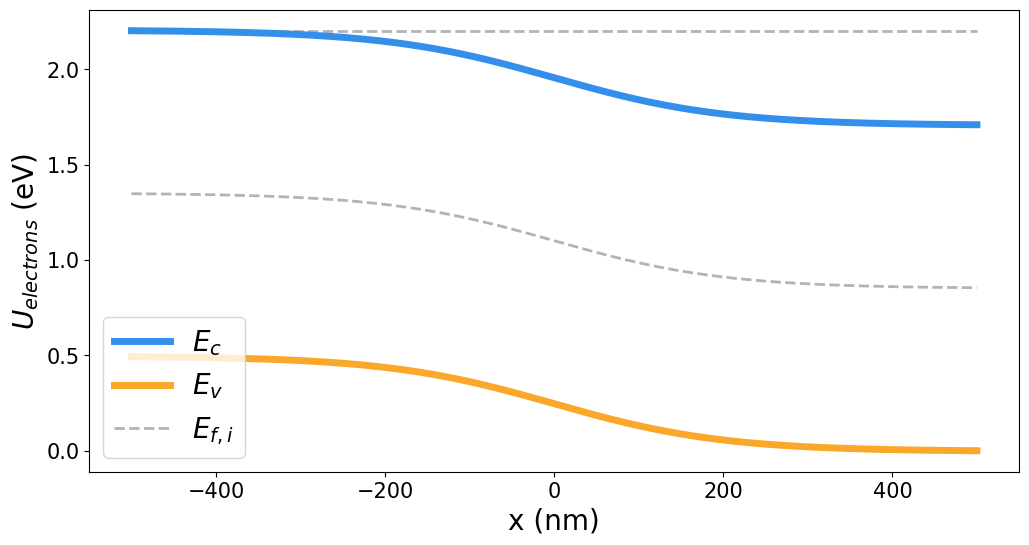
P-N JUNCTIONS: REVERSE BIAS
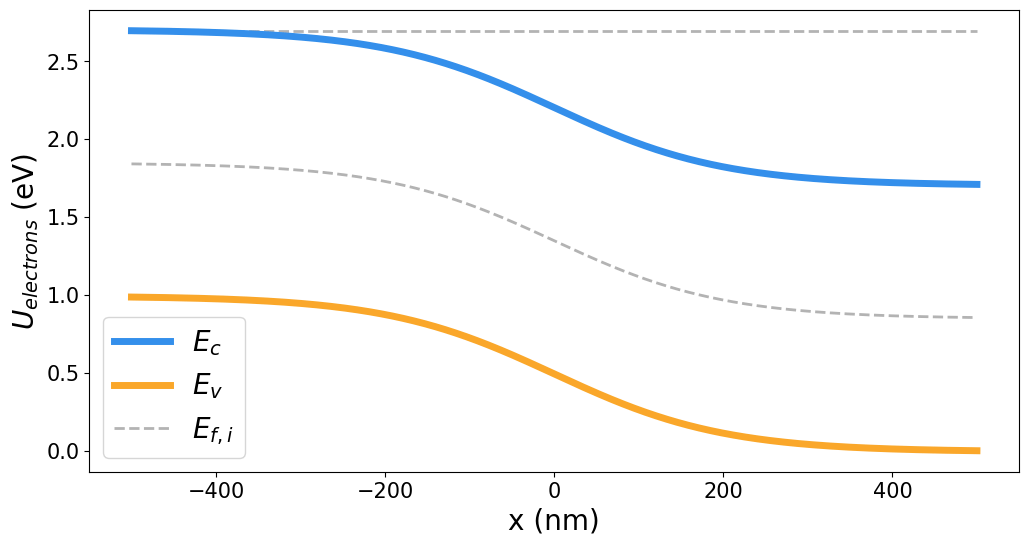
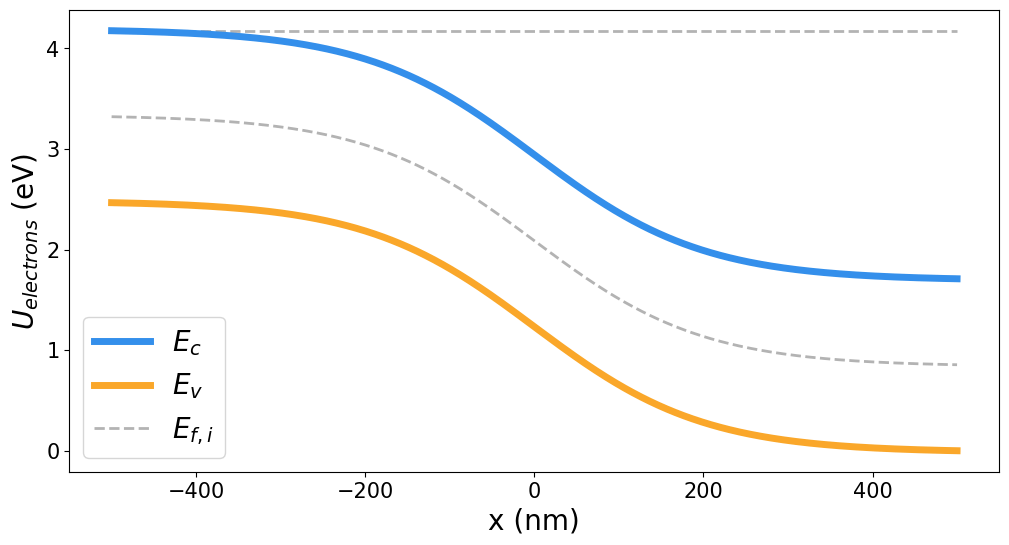
P-N JUNCTIONS: OUT OF EQUILIBRIUM
EXCESS OF INJECTED CARRIERS
\begin{dcases}
n_{p0} = n_{n0} e^{-\frac{e V_0}{k_B T}} \\[10pt]
p_{n0} = p_{p0} e^{-\frac{e V_0}{k_B T}} \\[10pt]
\end{dcases}
\Rightarrow
\begin{dcases}
n_{p}(0) = n_{n0} e^{-\frac{ e(V_0-V_{ext})}{k_B T}} \\[10pt]
p_{n}(0) = p_{p0} e^{-\frac{ e(V_0-V_{ext})}{k_B T}} \\[10pt]
\end{dcases}\\[5pt]
\Downarrow \\[5pt]
\begin{dcases}
\Delta n_{p}(0) = n_{p}(0)- n_{p0} = n_{p0} (e^{\frac{e V_{ext}}{k_B T}}-1) \\[10pt]
\Delta p_{n}(0) = p_{n}(0) - p_{n0} = p_{n0} (e^{\frac{e V_{ext}}{k_B T}}-1) \\[10pt]
\end{dcases}
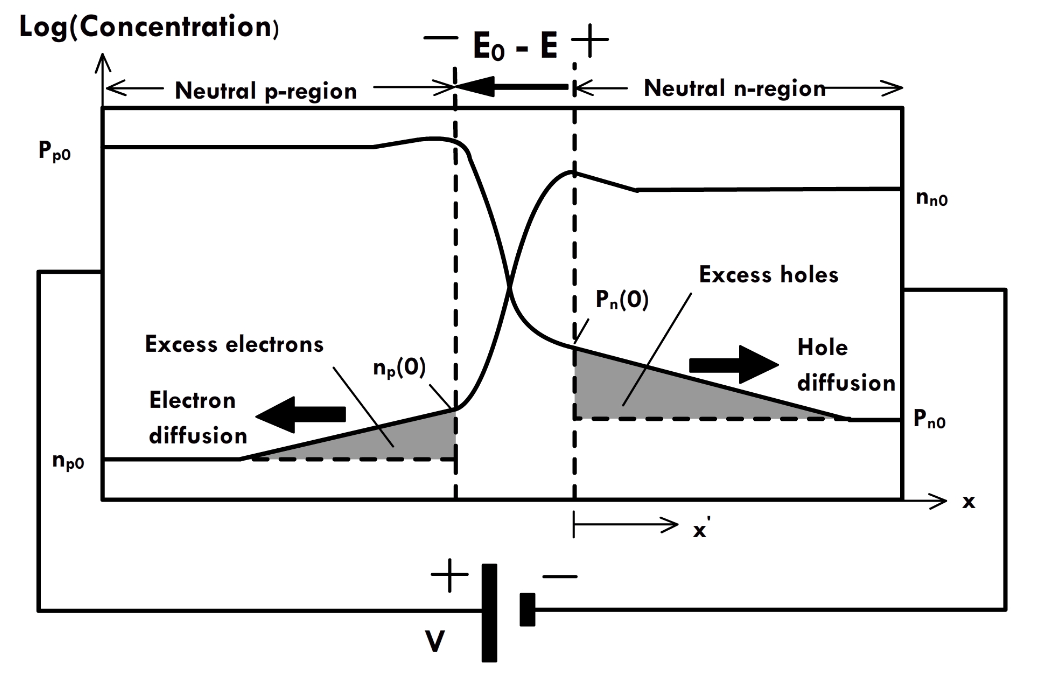
P-N JUNCTIONS: OUT OF EQUILIBRIUM
CONCENTRATION PROFILE OF EXCESS CARRIERS
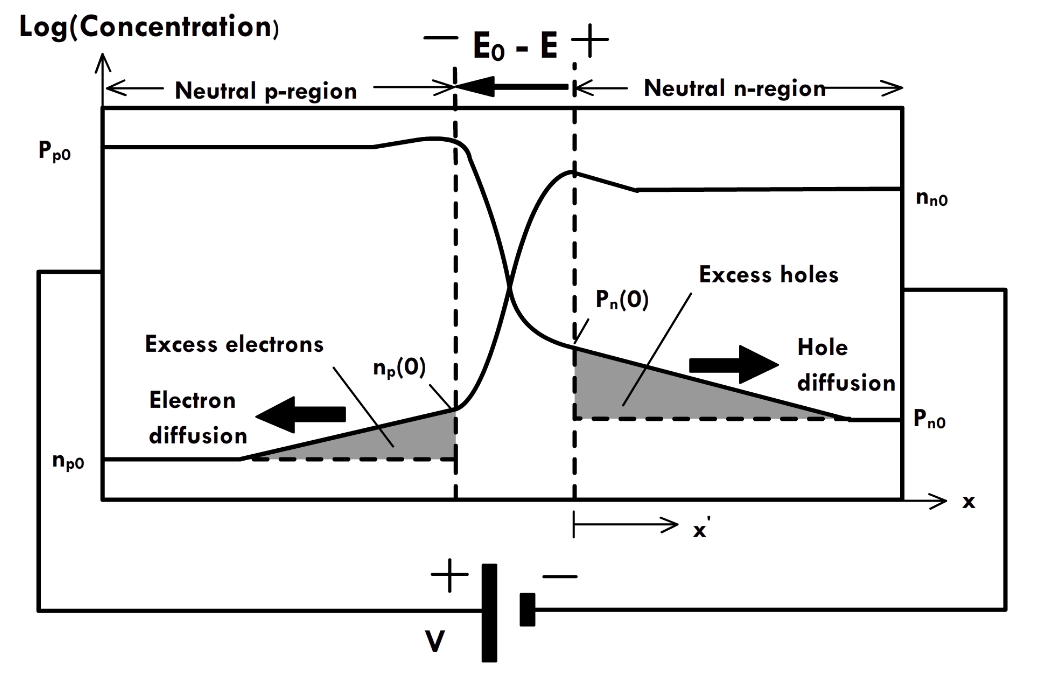
L_p=\sqrt{D_p \tau_p}\\
L_n=\sqrt{D_n \tau_n} \\
L_{p,n} \rightarrow \text{Diffusion length} \\
D_{p,n} \rightarrow \text{Diffusion coefficient} \\
\tau_{p,n} \rightarrow \text{Recombination time}
Diffusion Parameters
Einstein relation
D_p=\frac{k_B T \mu_p}{e} \\[10pt]
D_n=\frac{k_B T \mu_n}{e}
\begin{dcases}
p_n(x)=p_n(0) \exp \left(-\frac{x}{L_p}\right);\, \Delta p_n(x)= \Delta p_n(0) \exp \left(-\frac{x}{L_p}\right)\\
n_p(x)=n_p(0) \exp \left(-\frac{x}{L_n}\right); \, \Delta n_p(x)= \Delta n_p(0) \exp \left(-\frac{x}{L_n}\right)
\end{dcases}
Concentration Profile
P-N JUNCTIONS: OUT OF EQUILIBRIUM
DIFFUSION CURRENT DENSITY: Holes
J_{D,p}=-e D_p \frac{d p_n(x)}{d x} = -e D_p \frac{d \Delta p_n(x)}{d x} \\[5pt]
\Downarrow\\[5pt]
\begin{array}{r}
J_{D,p}=\frac{e D_p}{L_p} \Delta p_n(0)=\frac{e D_p}{L_p}\left(p_n(0)-p_{n 0}\right) \\
J_{D,p}=\frac{e D_p p_{n 0}}{L_p}\left[\exp \left(\frac{e V}{k_B T}\right)-1\right] \\
J_{D,p}=\frac{e D_p n_i^2}{L_p N_D}\left[\exp \left(\frac{e V}{k_B T}\right)-1\right]
\end{array}
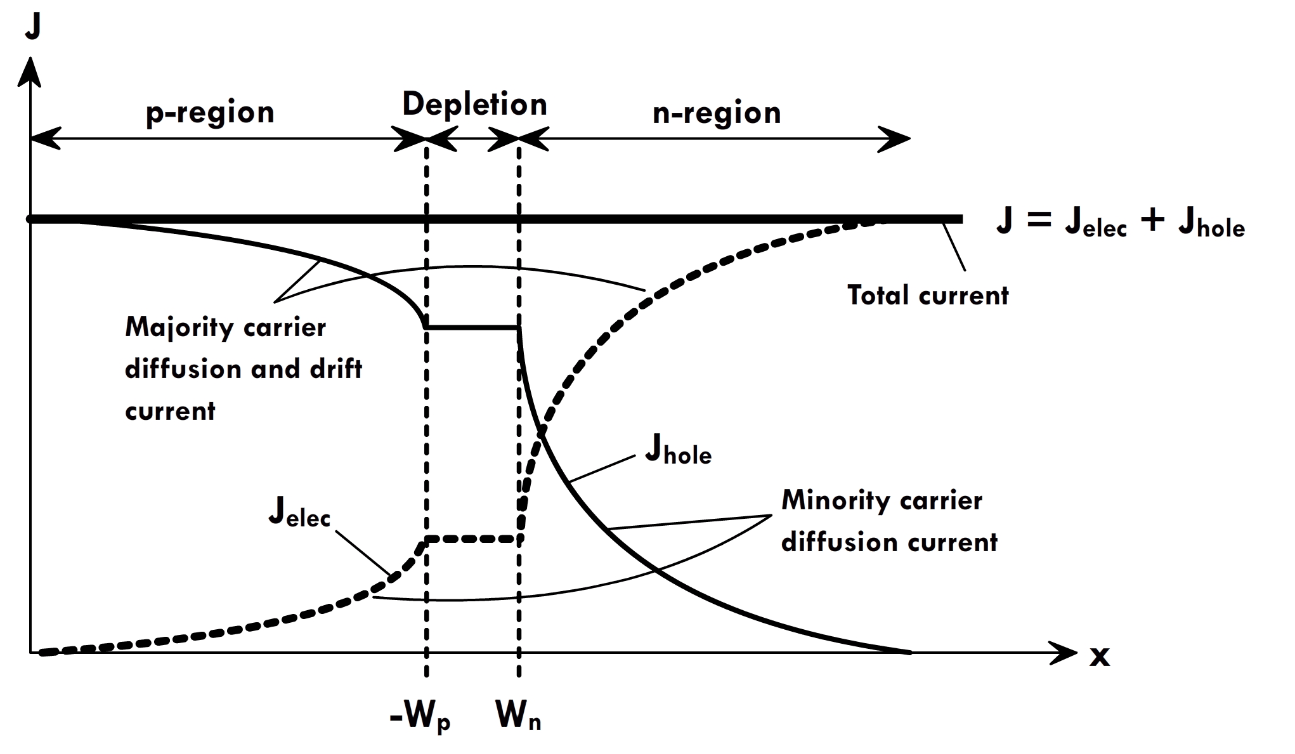
P-N JUNCTIONS: OUT OF EQUILIBRIUM
DIFFUSION CURRENT DENSITY: Electrons
J_{D,n}=e D_n \frac{d n_p(x)}{d x} = e D_n \frac{d \Delta n_p(x)}{d x} \\[5pt]
\Downarrow\\[5pt]
\begin{array}{r}
J_{D,n}=\frac{e D_n}{L_n} \Delta p_n(0)=\frac{e D_n}{L_n}\left(n_p(0)-n_{p 0}\right) \\
J_{D,n}=\frac{e D_n n_{p 0}}{L_n}\left[\exp \left(\frac{e V}{k_B T}\right)-1\right] \\
J_{D,n}=\frac{e D_n n_i^2}{L_n N_A}\left[\exp \left(\frac{e V}{k_B T}\right)-1\right]
\end{array}

P-N JUNCTIONS: I-V CURVE
\begin{gathered}
J_{s 0}=e n_i^2\left(\frac{D_p}{L_p N_D}+\frac{D_n}{L_n N_A}\right) \\
J_D=J_{s 0}\left[\exp \left(\frac{e V}{k_B T}\right)-1\right]
\end{gathered}
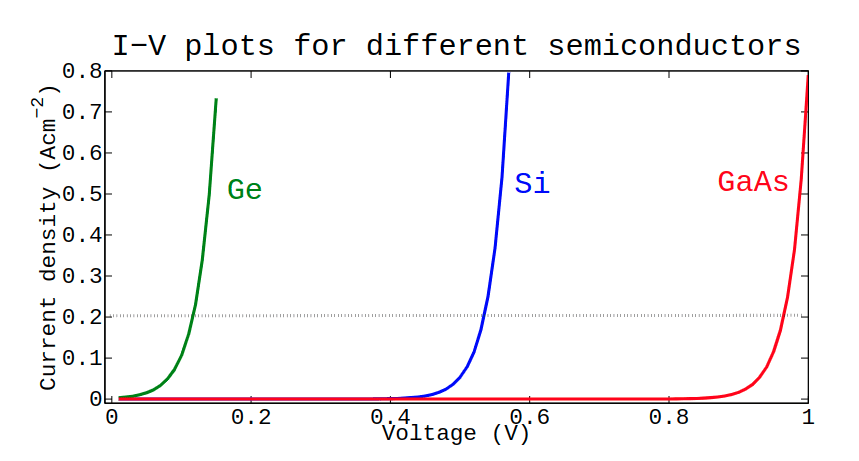
P-N JUNCTIONS: J-V CURVE
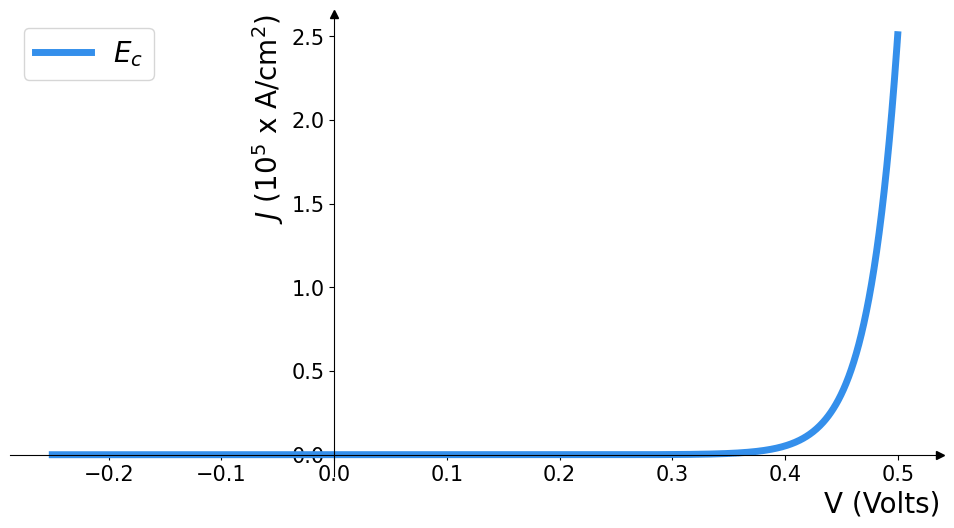
Materials and Platforms for AI - PN Junctions
By Giovanni Pellegrini
Materials and Platforms for AI - PN Junctions
- 165



