Title Text
Prior distributions
P(s\mid M)
uniform
P(M \mid s) \sim Dirichlet(\alpha)
We choose the Dirichlet distribution because it is conjugate to the multinomial likelihood
P(M|\{X\},s) \sim Dirichlet(\alpha + f(k,s,\{X\})
Accounting for phylogenetic relations
We are given phylogenetic tree
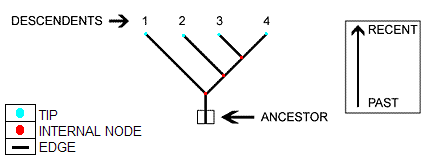
We model evolution for each base pair independently, using the Felsenstein model
We assume the motif represented by M, is the ancestor of all current sequences
Can then use a recursive algorithm for computing the likelihood
P_{\text{Fels}}(\{X\}\mid M,s)
P_{\text{Fels}}(\{X\}\mid M,s) P(M\mid s)
Problem
now has a very complicated functional form
Solution: Metropolis-Hastings
Sample using proposal probability
Accept with probability
\min\{1,\frac{P_{\text{Fels}}(\{X\}\mid M',s)\prod\limits_{b\in \{A,C,G,T\}}(M'_b)^f}{P_{\text{Fels}}(\{X\}\mid M,s)P(M\mid s)\prod\limits_{b\in \{A,C,G,T\}}(M_b)^f}\}
deck
By Guillermo Valle
