Heling Deng
Arizona State University
- Primordial black holes
- PBHs from bubbles
- Gravitational waves from PBHs
- Conclusions
- Primordial black holes
- PBHs from bubbles
- Gravitational waves from PBHs
- Conclusions
Black Hole
A region of spacetime from which no particles can escape due to strong gravity
-- Prediction of the theory of general relativity
Can be formed by dying stars: astrophysical BHs with mass
\sim 10 \ M_\odot
Supermassive BHs were discovered at galactic centers with mass
\sim 10^6\text{-}10^{11} \ M_\odot
which cannot be explained by astrophysical BHs
wikipedia
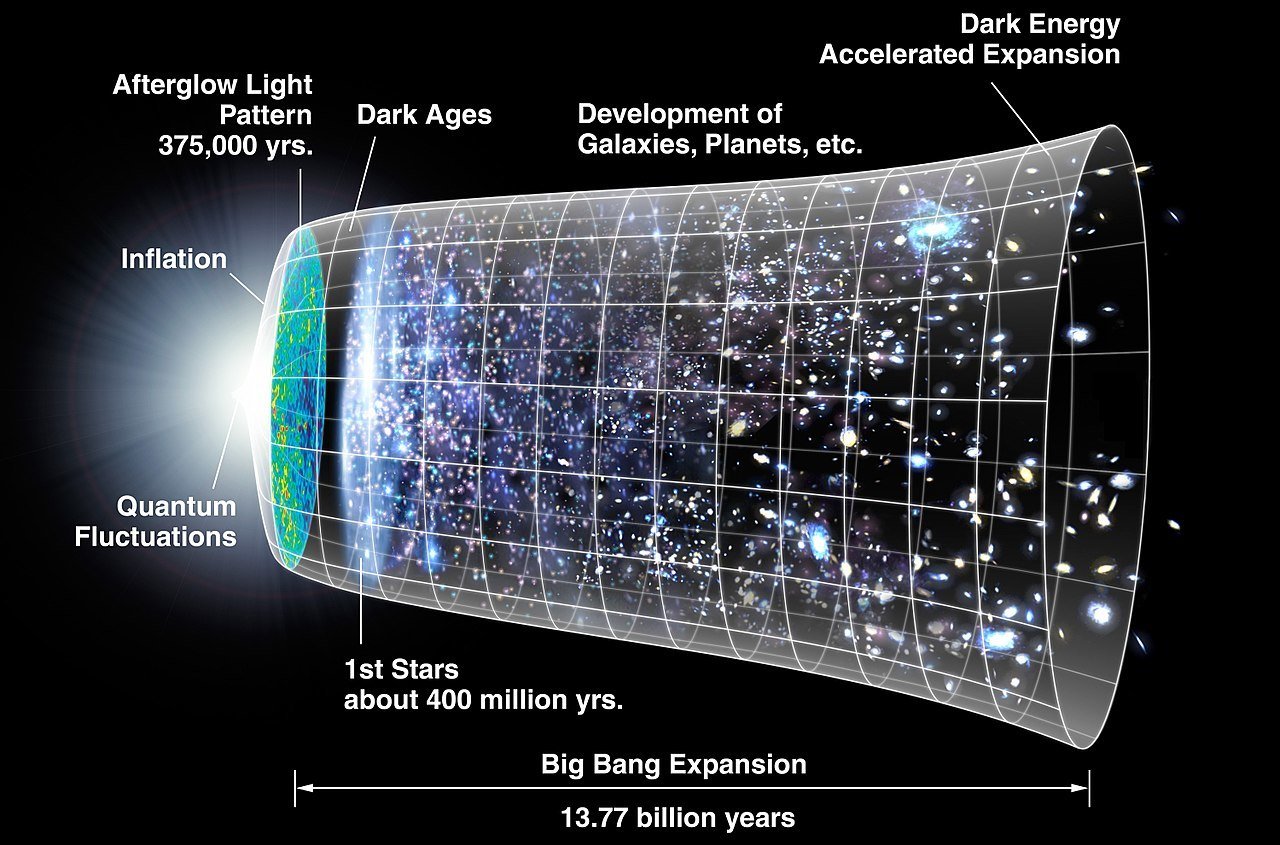
astro.uchicago.edu
- Primordial black holes
- PBHs from bubbles
- Gravitational waves from PBHs
- Conclusions
Physics beyond the "standard model" at high energy
Phase transition in the early universe \(\to\) Bubbles
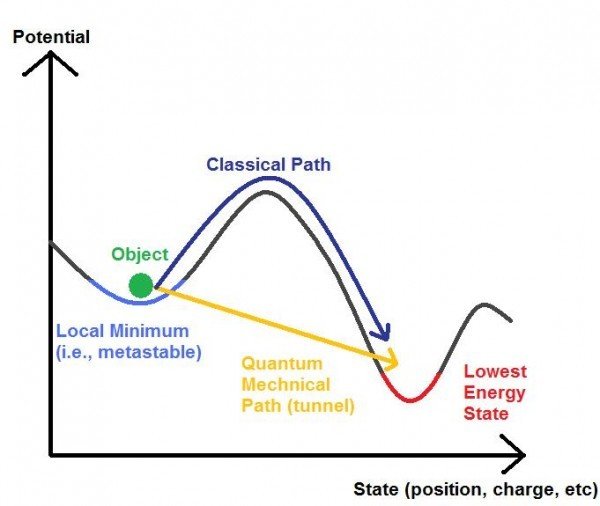
quantum tunneling
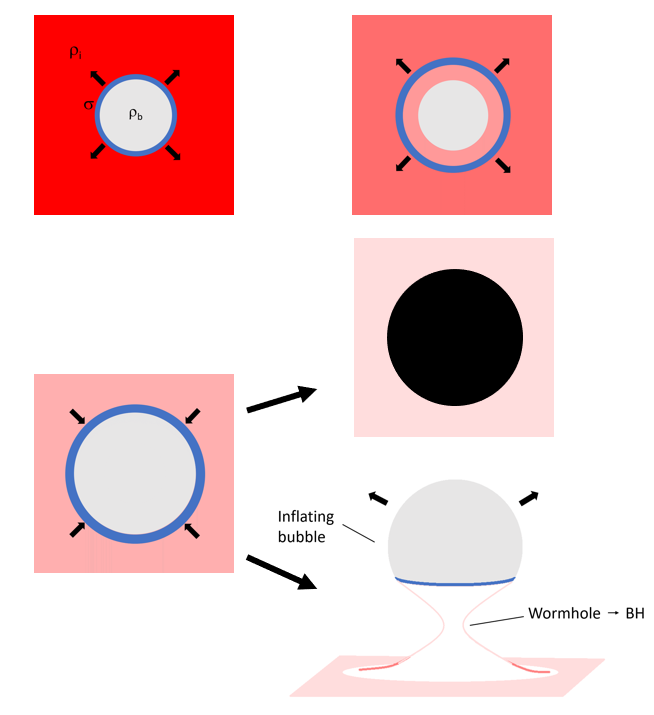
Fate of the bubble
subcritical
supercritical
Fate of the bubble
subcritical
supercritical
\(\Delta s^2\)= \(A^2(t,r)\Delta t^2 - B^2(t,r)\Delta r^2 - R^2(t,r)(\Delta \theta^2 + \sin\theta\Delta \phi^2)\)
Spherical spacetime (\(t,r,\theta,\phi\))
Radiation fluid: \(p=\frac{1}{3}\rho\)
\frac{A'}{A}=-\frac{\rho'}{4\rho}
\dot{U}=-A\left(\frac{4}{3}\pi\rho R+\frac{M}{R^2} \right)+\frac{A'\Gamma}{B}
\dot{\Gamma}=\frac{A'U}{B}
\dot{R}=AU
\dot{B}=\frac{AU'}{\Gamma}
\dot{\rho}=-\frac{4}{3}\rho A\left(\frac{U'}{B\Gamma}+\frac{2U}{R} \right)
where
U\equiv \frac{\dot{R}}{A}
\Gamma \equiv \frac{R'}{B}
M\equiv \frac{R}{2}\left(1-\Gamma^2 + U^2\right)
\rho/\rho_\text{FRW}
r
Early stage of evolution of \(\rho \)
r
\rho/\rho_\text{FRW}
Evolution of \(\rho \) after BH formation (subcritical)
r
\rho/\rho_\text{FRW}
Evolution of \(\rho \) at late time (subcritical)
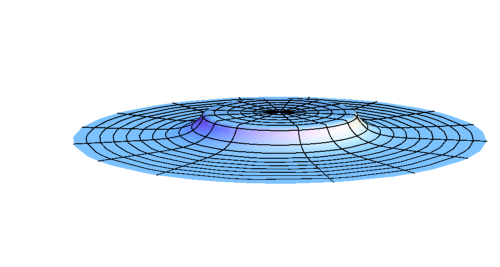
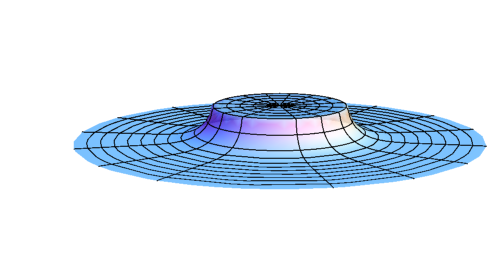
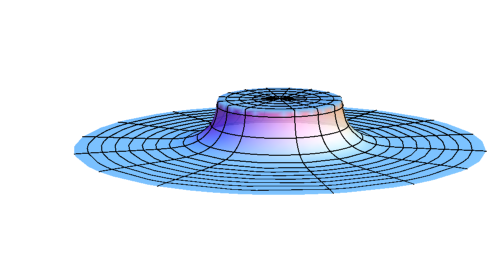
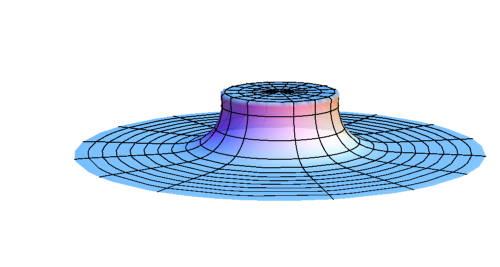
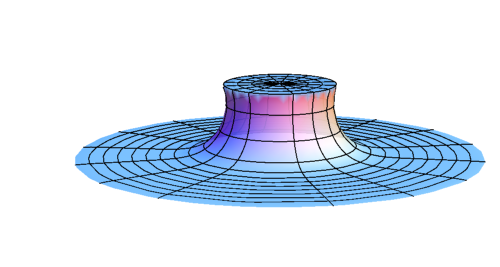
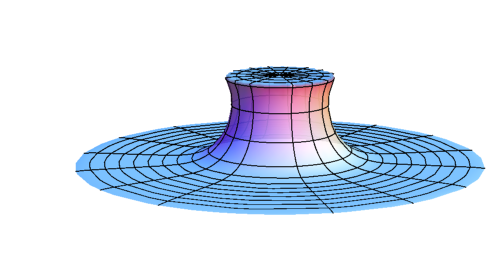
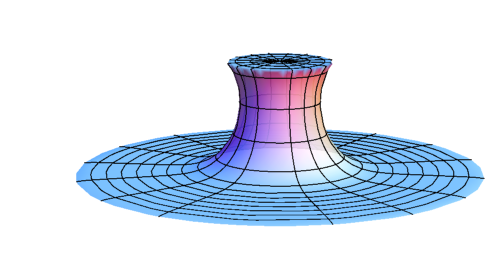
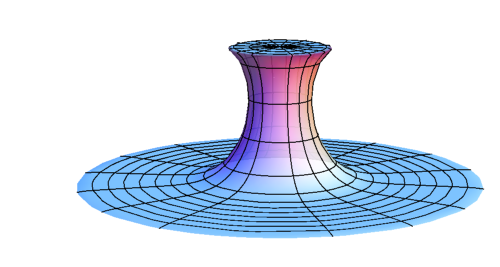
R
m\propto R^3
m\propto R^2
BH mass as a function of model parameters + Size distribution of bubbles\(\to\) BH mass distribution
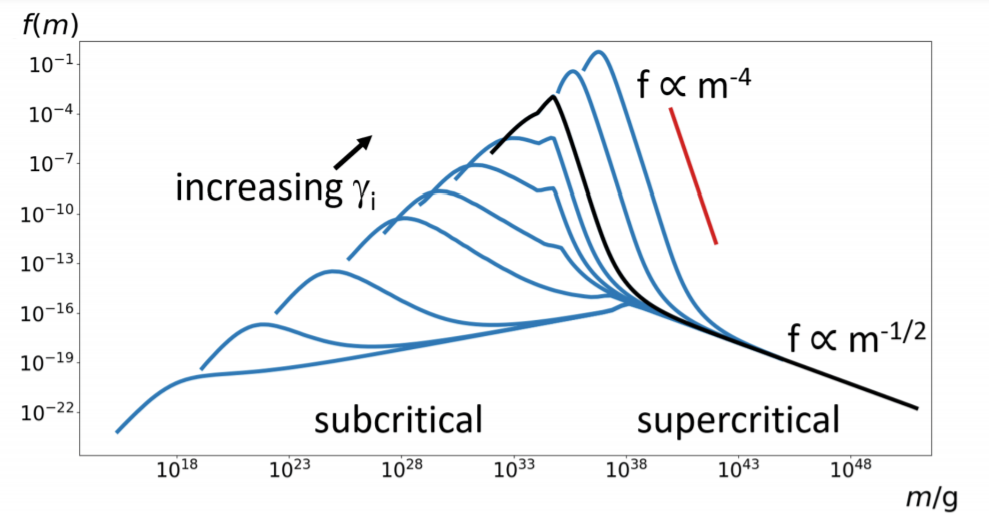
\(\sim 10M_\odot\)
- Primordial black holes
- PBHs from bubbles
- Gravitational waves from PBHs
- Conclusions
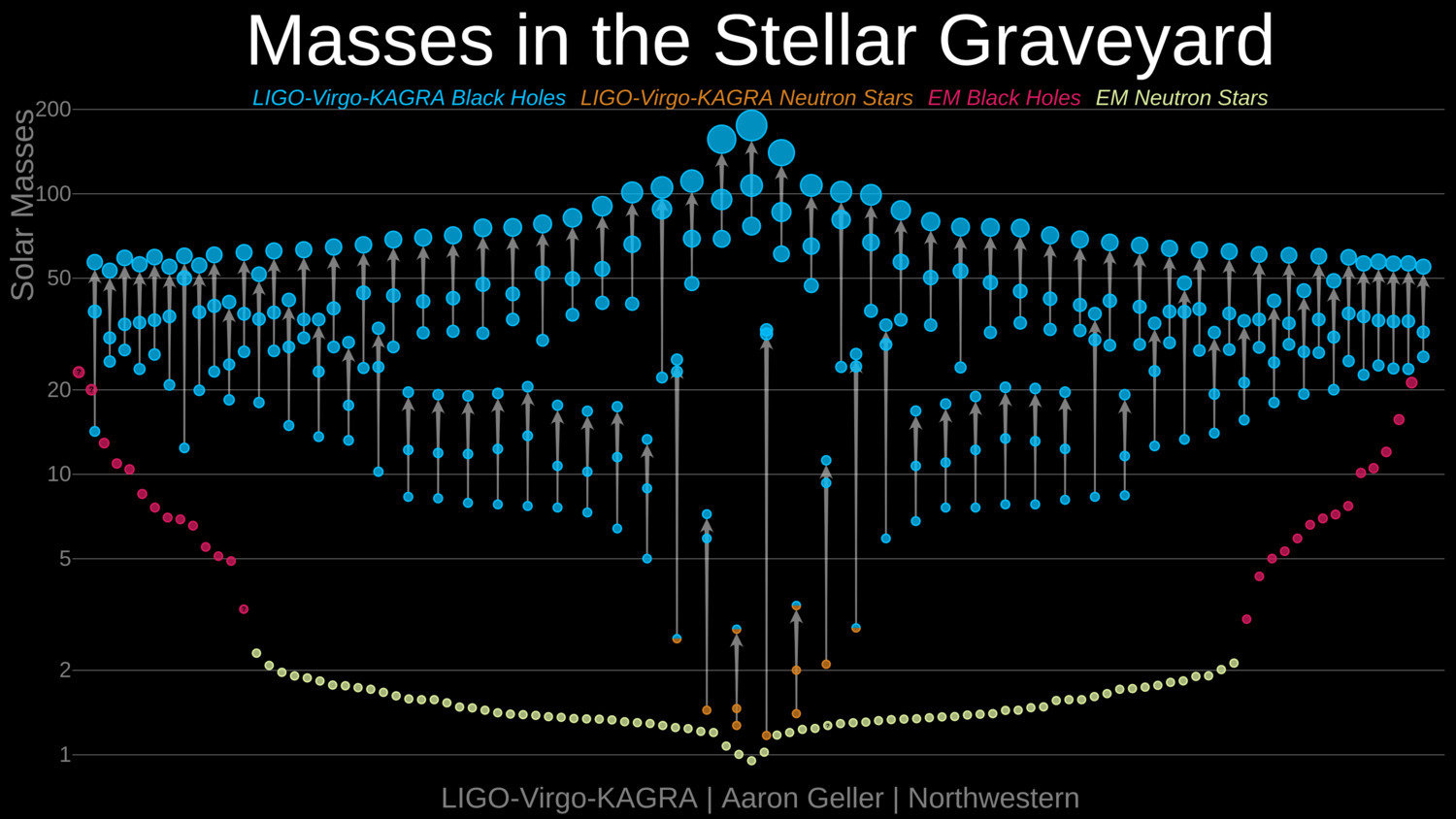
LIGO BHs
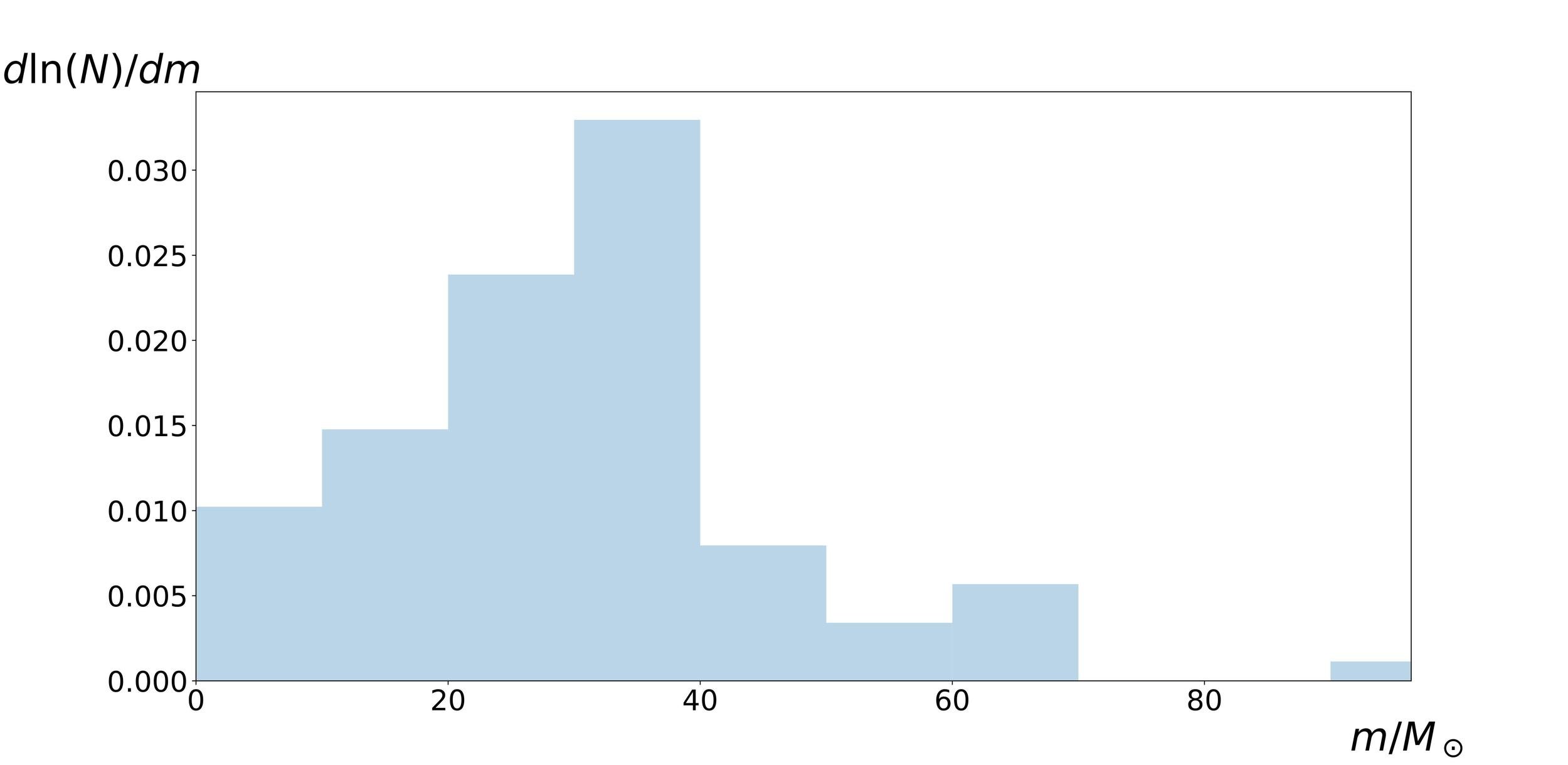
Mass distribution of LIGO BHs
PBH binary
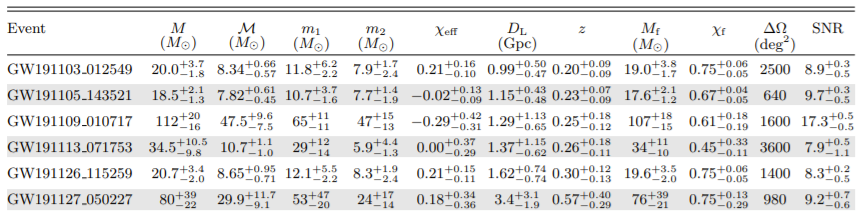
Dataset
Event: \((m_1,m_2,z)\)
Mass distribution of LIGO BHs
m^{\alpha_1},\ \ \ m< m_*
m^{\alpha_2},\ \ \ m> m_*
f(m)\propto
\{
A simple mass function
\log(m)
\log(f)
m^{\alpha_1}
m^{\alpha_2}
m_*
f_{PBH}
f_{PBH}
PBH mass function
Merger rate
Detection probability
Probability of each event \(p_i(m_1,m_2,z)\)
+
Likelihood of all LIGO events
+
Expected number of detection \(N_e\)
p_{Poisson}\propto N_e^{N_o}e^{-N_e}
\mathcal{L}\propto p_{Poisson}\prod_{i=1}^{N_o} p_i
Mergers reaching earth today
Signals follow a Poisson process
f_{PBH}\approx 10^{-3}
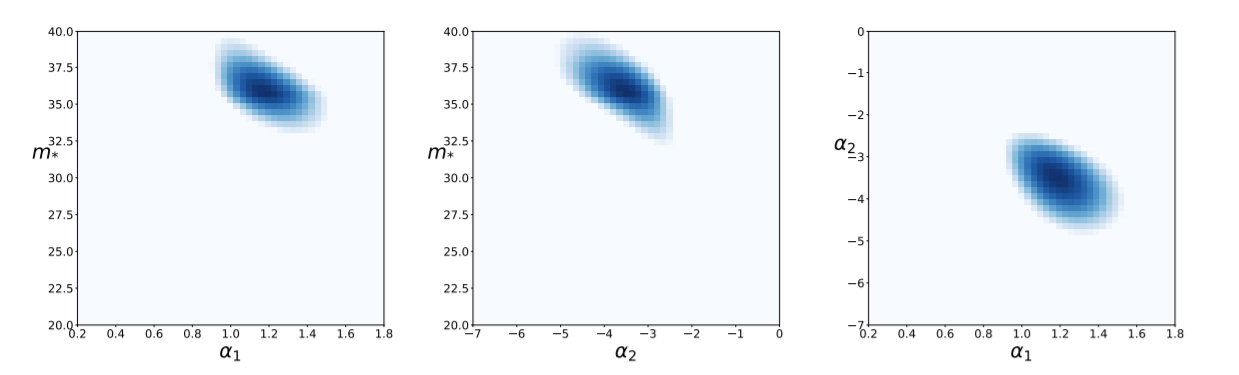
Maximizing \(\mathcal{L}\) in a 4-parameter space
\alpha_2 = -4
\alpha_1 = 1.2
m_*=35M_\odot
\log(m)
\log(f)
m^{1.2}
m^{-4}
35M_\odot
10^{-3}
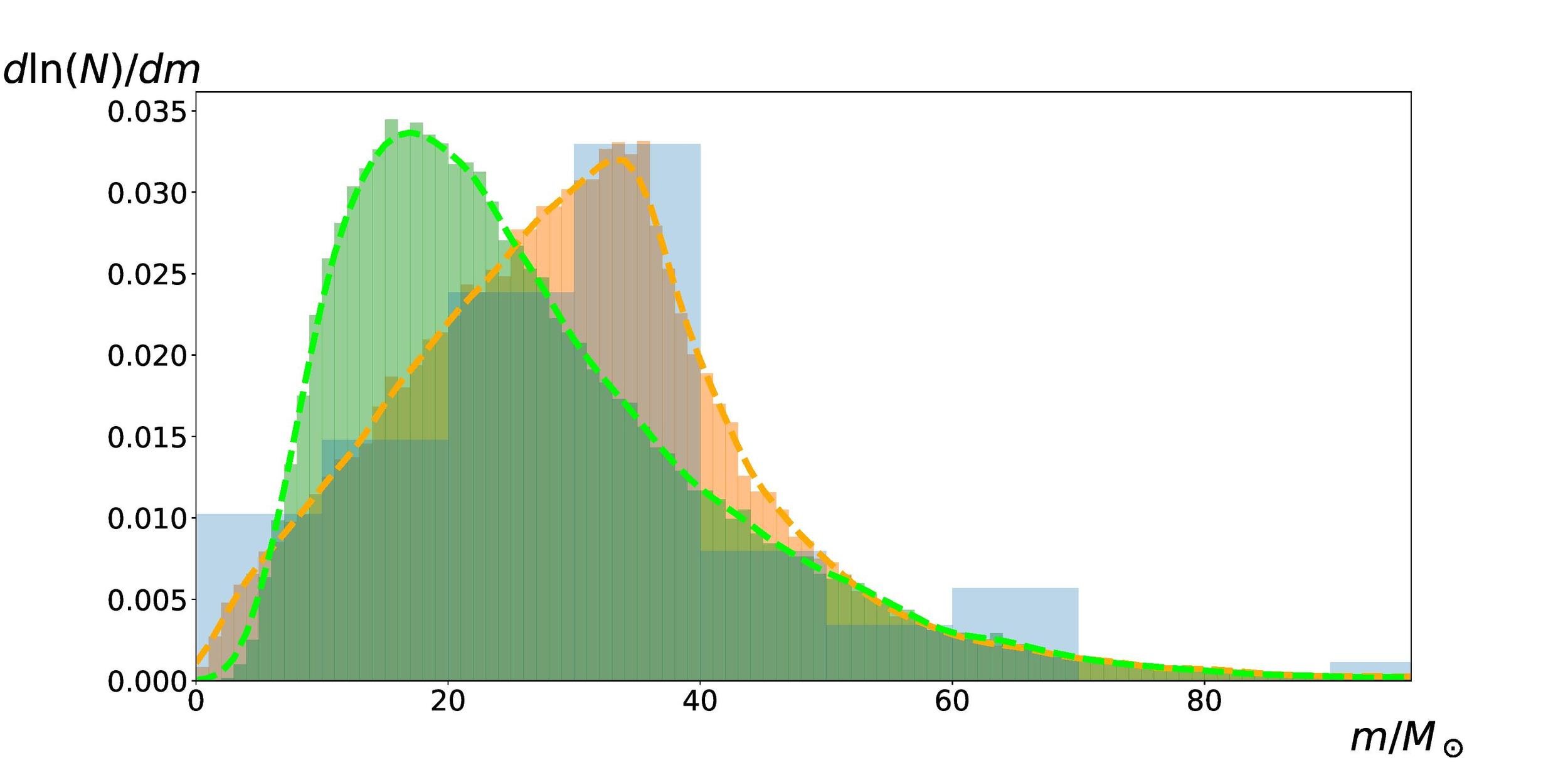
Is there a mechanism that can provide such a mass function?
subcritical
supercritical
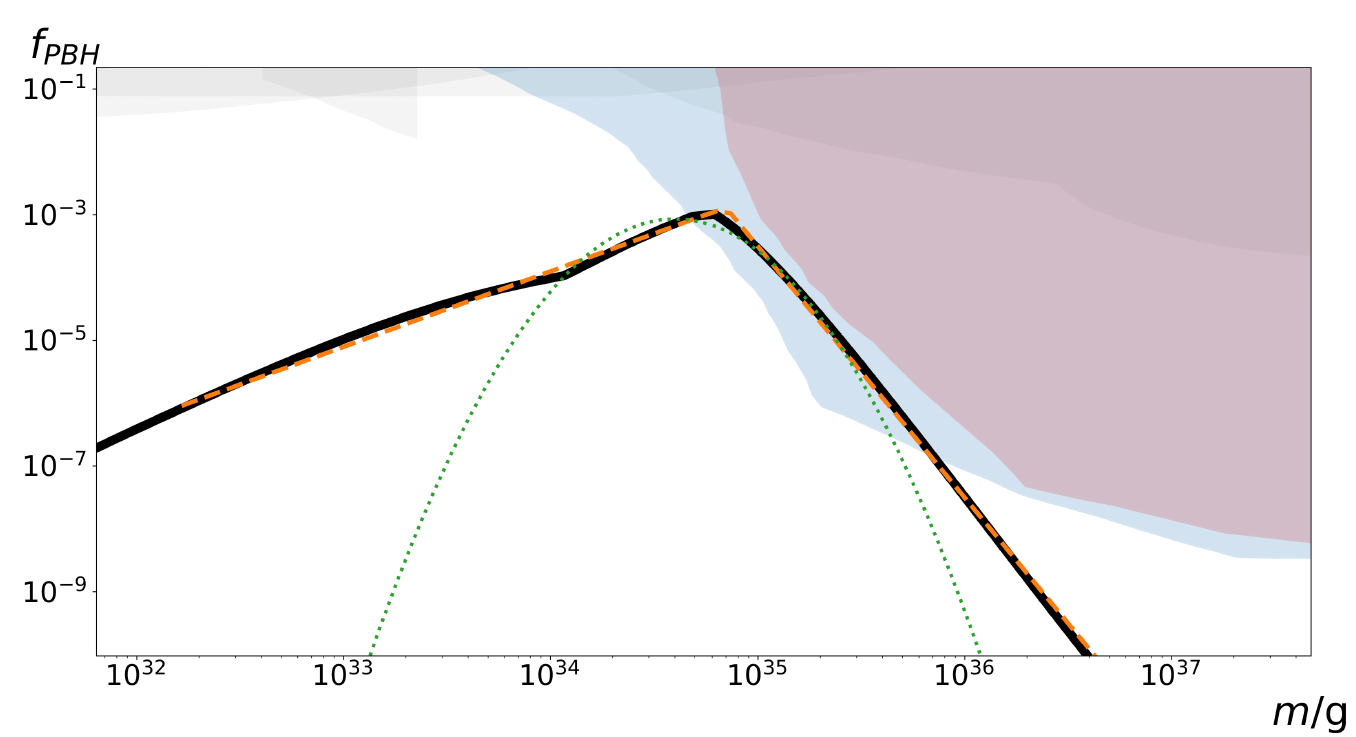
Conclusions
- Primordial bubbles can be formed in the early universe due to phase transition
- Depending on their sizes after the big bang, bubbles can be classified into two categories: subcritical and supercritical, both leading to black hole formation
- PBH mass spectrum can range over many orders of magnitude
- With some parameter choices, these PBHs can account for SMBHs and black hole mergers observed by LIGO
PBHs from Primordial Bubbles
By Heling Deng
