Revisiting gravitational wave background from primordial black holes
Heling Deng
邓鹤凌
Arizona State University
2110.02460
Outline
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
Outline
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
M_\text{Pl} \newline
\sim10^{-5}\ \rm g
M_\text{evp} \newline \sim10^{15}\ \rm g
M_\odot \newline \sim10^{33}\ \rm g
M_\text{PBH}
LIGO BHs
Supermassive black holes
\mathcal O (10) \ M_\odot
SMBHs
...
...
Primordial black holes (PBHs)
\mathcal{O}(10^6 \text{-} 10^{10})M_\odot
M_\text{Pl} \newline
\sim10^{-5}\ \rm g
M_\text{evp} \newline \sim10^{15}\ \rm g
M_\odot \newline \sim10^{33}\ \rm g
M_\text{PBH}
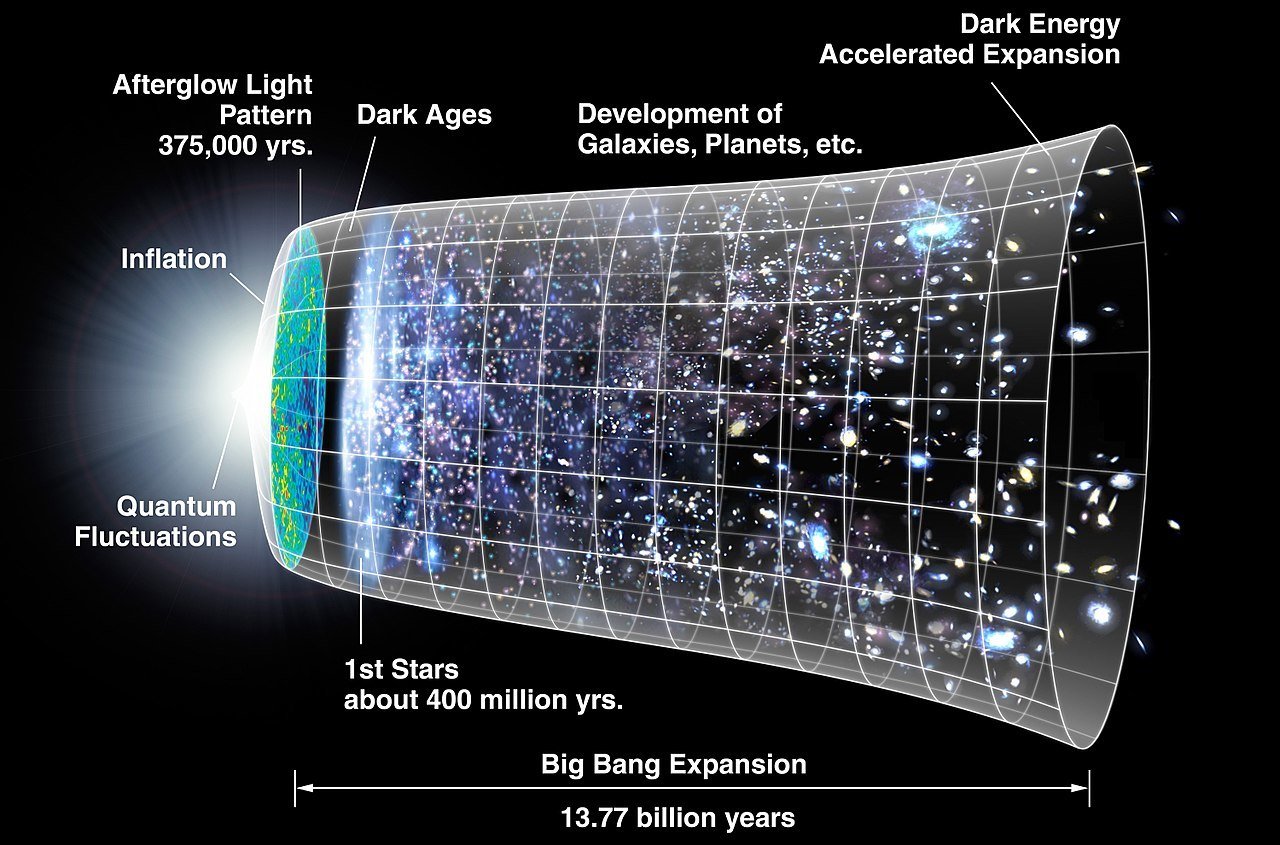
LIGO BHs
Supermassive black holes
LIGO black holes
\mathcal O (10) \ M_\odot
SMBHs
...
...
Astrophysical BHs
Primordial black holes (PBHs)
\mathcal{O}(10^6 \text{-} 10^{10})M_\odot
LIGO BHs
M_\text{Pl} \newline
\sim10^{-5}\ \rm g
M_\text{evp} \newline \sim10^{15}\ \rm g
M_\odot \newline \sim10^{33}\ \rm g
M_\text{PBH}
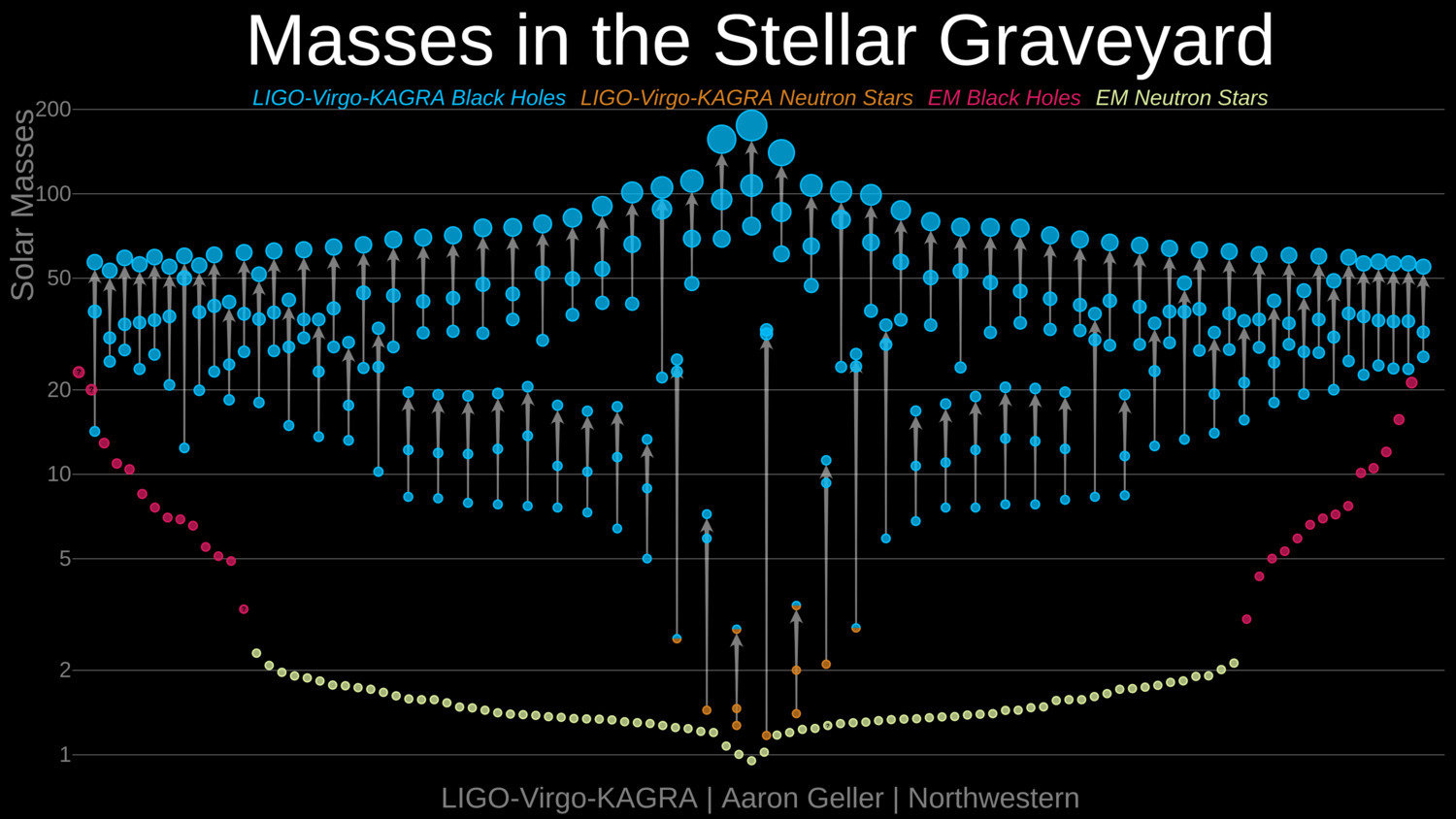
LIGO BH
Supermassive black holes
LIGO black holes
Dark matter
\mathcal O (10\text{-} 100) \ M_\odot
SMBH
...
...
Primordial black holes (PBHs)
\mathcal{O}(10^6 \text{-} 10^{10})M_\odot
Astrophysical BHs
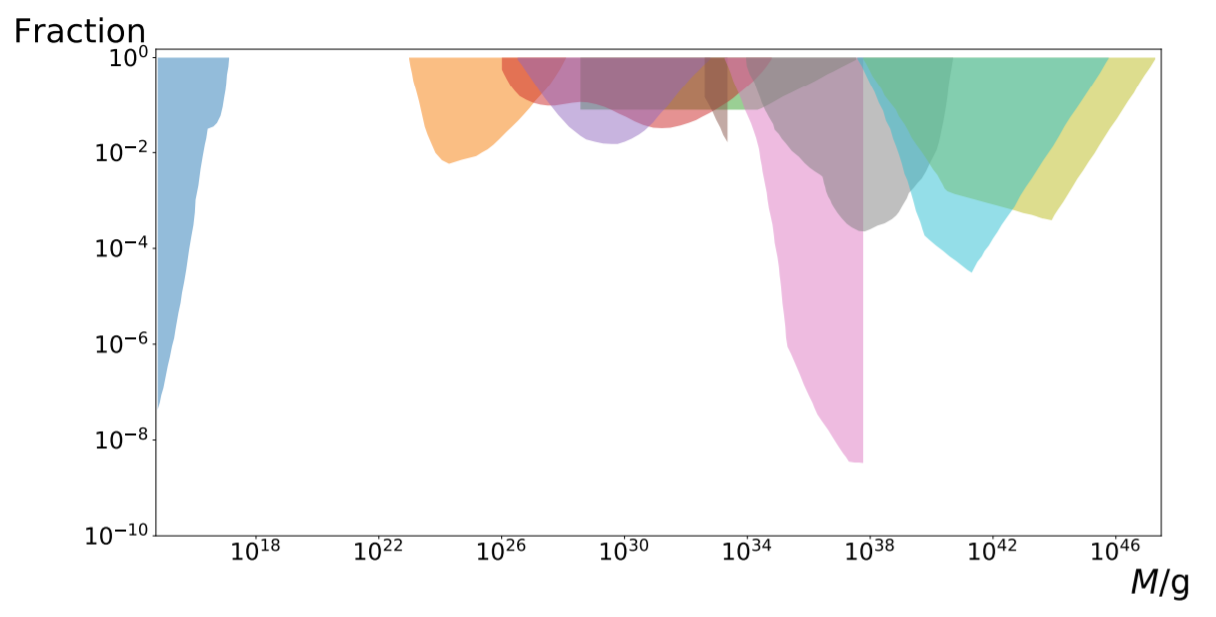
Observational constraints of monochromatic PBHs as DM
Outline
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
PBH binary
PBH binary
free-fall time
Hubble time
When do two neighboring PBHs decouple from Hubble flow?
<
PBH binary
\(y\)
\({x}\)
At dust-radiation equality (\(z_{eq}\sim3000\))
\(\rho\) -- dark matter density
\(M\) -- PBH mass
\(f\) -- fraction of dark matter in PBHs
\(\to\) \(n\sim \bar{x}^{-3} \sim\frac{f\rho}{M}\)
- \(\bar{x}\) -- average physical separation between two PBHs
- \({x}\) -- physical distance between two neighboring PBHs without Newton
- \(y\) -- physical distance from the third nearby PBH to the binary
PBH binary
Two neighboring PBHs decouple from Hubble flow when
free-fall time < Hubble time
\(\to\)
- \(z_{dec}>z_{eq}\)
- physical separation when decouple is \(a=\left(\frac{z_{eq}}{z_{dec}}\right)x=\frac{x^4}{f\bar{x}^3}\)
\(y\)
\({x}\)
PBH binary
\(a\)
Initial semi-major axis: \(a\sim\frac{x^4}{f\bar{x}^3}\)
Coalescence time given by the Peters formula
P. C. Peters, Phys. Rev. 136, B1224 (1964)
\(t_P \propto \frac{a^4}{M^3}(1-e^2)^{7/2}\)
Initial eccentricity: \(\sqrt{1-e^2}\sim \left(\frac{x}{y}\right)^3\)
\(\propto \frac{x^{37}}{y^{21}}\)
For a random PBH, the probability that a second BH is at \((x, x+\text{d}x)\) and a third BH is at \((y, y+\text{d}y)\) is
\(P(x,y)\text{d}x\text{d}y=\mathcal{O}(10)n^2x^2y^2\text{d}x\text{d}y\)
\(y\)
\({x}\)
PBH binary
\(\to\) For a random PBH, the probability that a merger occurs at \((t, t+\text{d}t)\) is
\(P(t)\text{d}t=\mathcal{O}(10)n^2\int x^2y^2|\frac{\text{d}x}{\text{d}t}|\text{d}y\text{d}t\)
Peters formula: \(t\propto\frac{x^{37}}{y^{21}} \to x\propto\left(\frac{y^{21}}{t}\right)^{1/37}\)
PBH binary
Peters formula: \(t\propto\frac{x^{37}}{y^{21}} \to x\propto\left(\frac{y^{21}}{t}\right)^{1/37}\)
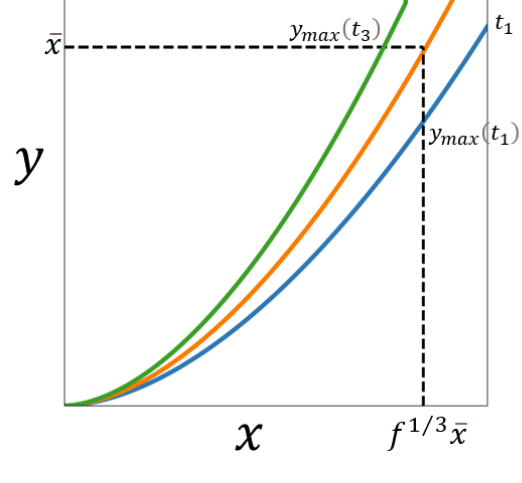
bounds:
- \(x<f^{1/3}\bar{x}\) -- ensure the binary is formed during the radiation era
- \(y<\bar{x}\) -- probability that two PBHs with separation > \(\bar{x}\) is exponentially suppressed
curves with constant \(t\)
Integration largely determined by \(y_{max}\)
\(t_2\)
\(t_3\)
\(t_1>t_2>t_3\)
\(P(t)\propto\int x^2y^2|\frac{\text{d}x}{\text{d}t}|\text{d}y\)
PBH binary
\(P(t)\propto\int x^2y^2|\frac{\text{d}x}{\text{d}t}|\text{d}y\)
results:
\(P(t)\approx\frac{0.005f}{t}\)
{
\(\left(\frac{t}{t_c}\right)^{-1/7},\ t > t_c\)
\(\left(\frac{t}{t_c}\right)^{3/37},\ t < t_c\)
where \(t_c\sim 10^{42}f^7\left(\frac{M}{M_\odot}\right)^{-5/3}\ \text{s}\)
curves with constant \(t\)
\(t_2\)
\(t_3\)
\(t_1>t_2>t_3\)
\(t_2=t_c\)
1603.08338, Sasaki, Suyama, Tanaka and Yokoyama
Example:
\(M=10M_\odot, f=0.1\% \to t_c\sim 10^{19}\ \text{s}\)
\(M=100M_\odot, f=0.1\% \to t_c\sim 10^{17}\ \text{s}\)
Peters formula: \(t\propto\frac{x^{37}}{y^{21}} \to x\propto\left(\frac{y^{21}}{t}\right)^{1/37}\)
Outline
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
PBH binary
\(a\)
Coalescence time given by the Peters formula
P. C. Peters, Phys. Rev. 136, B1224 (1964)
\(t_P \propto \frac{a^4}{M^3}(1-e^2)^{7/2}\)
\(e \to 1, t_p \to 0?\)
free-fall time: \(t_{ff}\sim \sqrt{\frac{a^3}{M}}\)
Coalescence time can be estimated by Peters formula only if \(t_P > t_{ff}\)
PBH binary
\(a\)
Peters formula: \(t_P \propto \frac{a^4}{M^3}(1-e^2)^{7/2}\)
free-fall time: \(t_{ff}\sim \sqrt{\frac{a^3}{M}}\)
\(t\sim t_P+t_{ff}\)
Coalescence time should be
PBH binary
Peters formula: \(t= t_P(x,y) \to x=F(y)\)
curves with constant \(t\)
Integration largely determined by \(y_{max}\)
\(t_2\)
\(t_3\)
\(t_1>t_2>t_3\)
\(P(t)\propto\int x^2y^2|\frac{\text{d}x}{\text{d}t}|\text{d}y\)
PBH binary
\(t= t_P+t_{ff} = \frac{3\rho^4}{170M^7}\frac{x^{37}}{y^{21}} + \frac{\rho^{3/2}}{M^2}x^6\)
\(\to y\propto\left(\frac{x^{37}}{M^2\rho^{-3/2}t-x^6}\right)^{1/21}\)
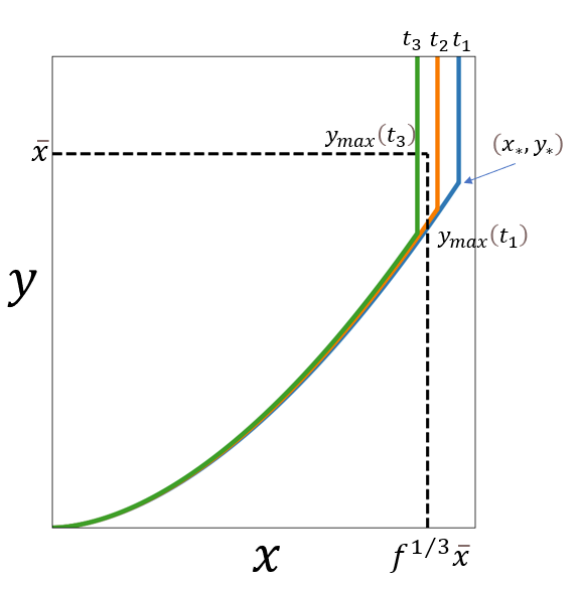
Integration largely determined by \(y_{max}\)
\(t_1>t_2>t_3\)
**PBH binaries could have a significantly larger merger rate "at some point" than previously expected**
\(P(t)\propto\int x^2y^2|\frac{\text{d}x}{\text{d}t}|\text{d}y\)
Peters formula: \(t\propto\frac{x^{37}}{y^{21}} \to x\propto\left(\frac{y^{21}}{t}\right)^{1/37}\)
Outline
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
GWB from PBH mergers
\(\Omega_{GW}(\nu_d)=\frac{\nu_d}{\rho_c}\int N(z)\frac{\text{d}E_{GW}(\nu_s)}{\text{d}\nu_s}|_{\nu_s=\nu_d(1+z)}\text{d}z\)
- \(N(z)\text{d}z\) -- comoving number density of events at \((z,z+\text{d}z)\)
- \(v_d\) -- GW frequency in detector
- \(\nu_s\) -- GW frequency in source
- \(\frac{\text{d}E_{GW}(\nu_s)}{\text{d}\nu_s}\) -- GW energy spectrum from a single event
for PBH merger:
\(N(z)\text{d}z=nz_{eq}^{-3}P(t)\text{d}t\)
\(\frac{\text{d}E_{GW}(\nu_s)}{\text{d}\nu_s}\) from numerical relativity
\(\Omega_{GW}\) has a peak near \(\nu \sim 10^4(M/M_\odot)^{-1}\ \text{Hz}\)
1903.05924, Wang, Terada and Kohri
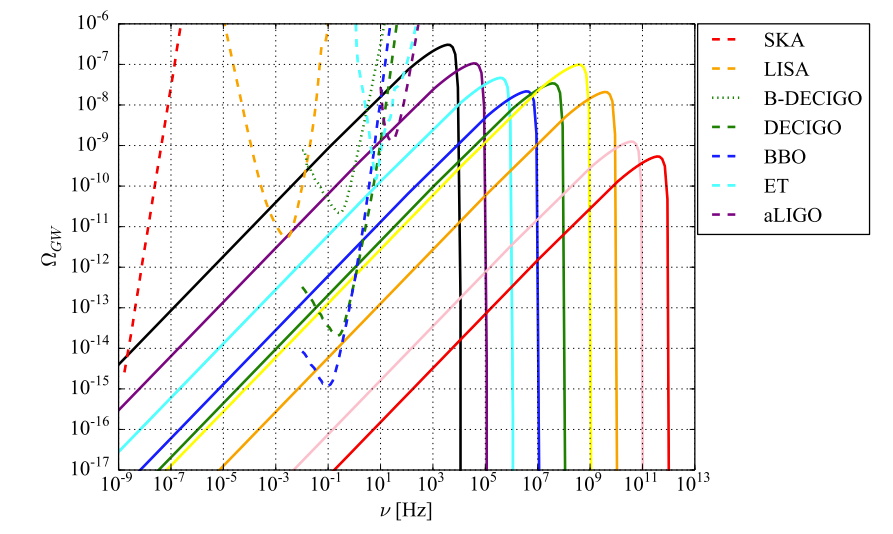
Examples of \(\Omega_{GW}\) from PBH mergers
\(\Omega_{GW}\) has a peak near \(\nu \sim 10^4(M/M_\odot)^{-1}\ \text{Hz}\)
\(t_1>t_2>t_3\)
**PBH binaries could have a significantly larger merger rate "at some point" than previously expected**
Examples of \(\Omega_{GW}\) from PBH mergers taking into account the "free-fall time" effect
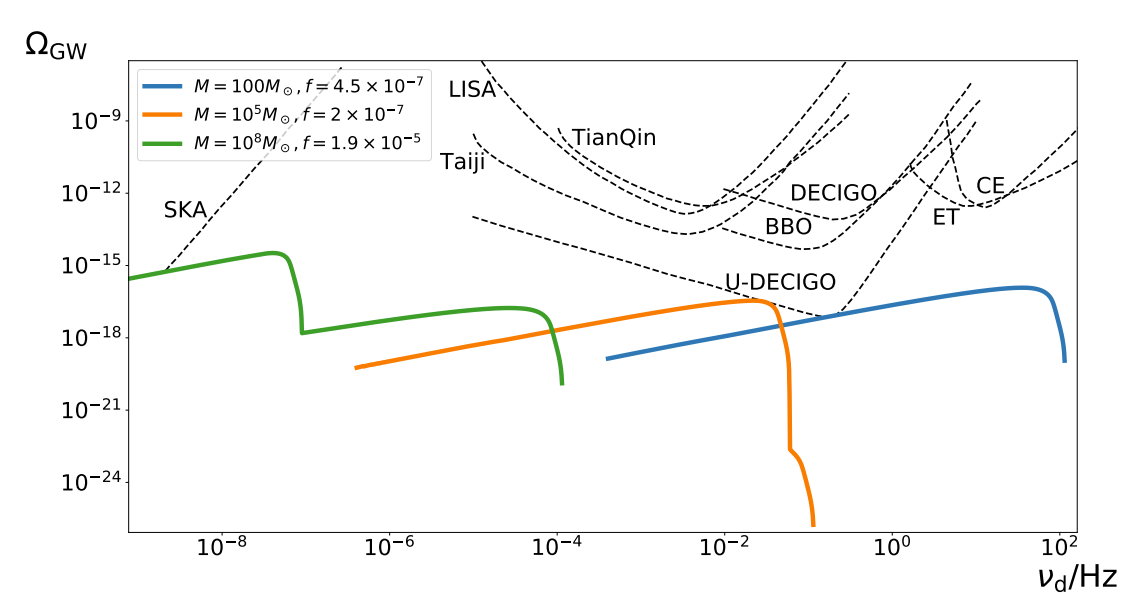
More stringent constraints on PBHs if we don’t see GWB in the future
Observational constraints of monochromatic PBHs as DM
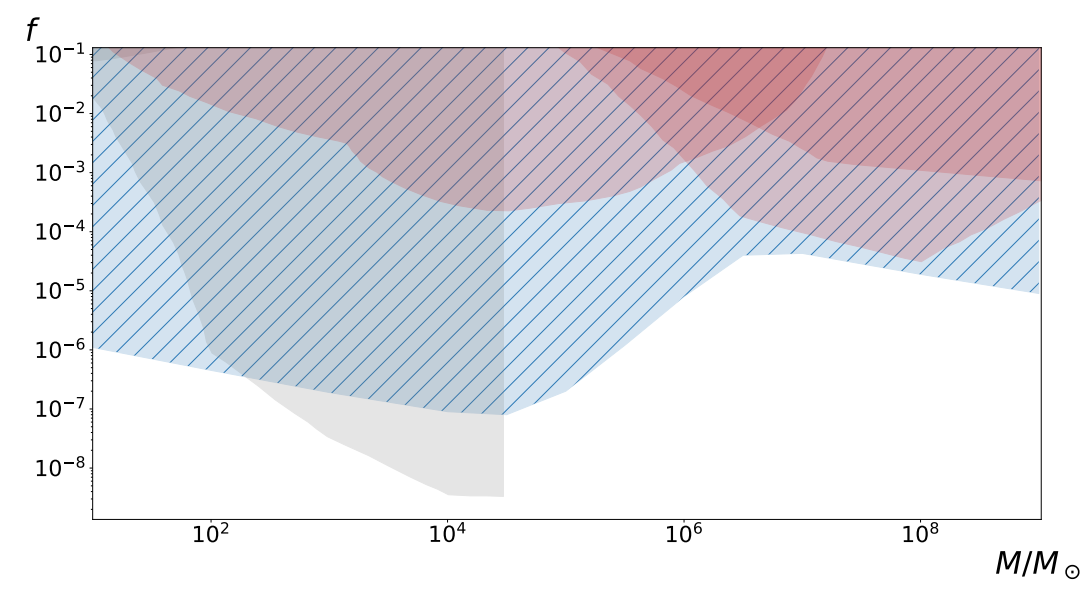
Observational constraints of large PBHs as DM
- Primordial black holes
- PBH binary merger rate
- Gravitational wave background from PBH mergers
- Revisiting PBH binary merger rate
- Mass accretion
Outline
PBHs absorb ambient gas and dark matter after dust-radiation equality and could grow by orders of magnitude
However, details are still unclear
We consider accretion from \(z=30\) to \(z=10\) (\(t\sim 10^{16}\ \text{s}\))
\(P(t)\approx\frac{0.005f}{t}\)
{
\(\left(\frac{t}{t_c}\right)^{-1/7}-f\left(\frac{t}{t_{last}}\right)^{3/8},\ t > t_c\)
\(\left(\frac{t}{t_c}\right)^{3/37},\ t < t_c\)
PBH merger rate
where \(t_{last}\sim 10^{42}\left(\frac{M}{M_\odot}\right)^{-5/3}\ \text{s}\)
Example: for \(M=100M_\odot\), we have \(t_{last}\sim 10^{39}\ \text{s}\)
\(P(t_{last})=0\)
In the presence of accretion at \(t\sim 10^{16}\ \text{s}\), the change in black hole mass alters the binary orbit, and thus the PBH merger rate
\(a\)
\(\frac{\dot{a}}{a}+3\frac{\dot{M}}{M}=0\)
\(t_P\propto \frac{a^4}{M^3}\)
Coalescence time decreases from \(t\) to
\(t_{acc}=\left(\frac{M_f}{M_i}\right)^{-15}t\)
\(\to a \propto M^{-3}\)
eccentricity remains const
2005.05641, De Luca, Franciolini, Pani and Riotto
could be tiny!
Example: for \(M=100M_\odot\), we have \(t_{last}\sim 10^{39}\ \text{s}\)
for \(M_i=100M_\odot\) and \(M_f=10000M_\odot\), we have \(t_{acc}=\left(\frac{M_f}{M_i}\right)^{-15}t_{last}=10^9\ \text{s}\)!
**Aggregated mergers during accretion**
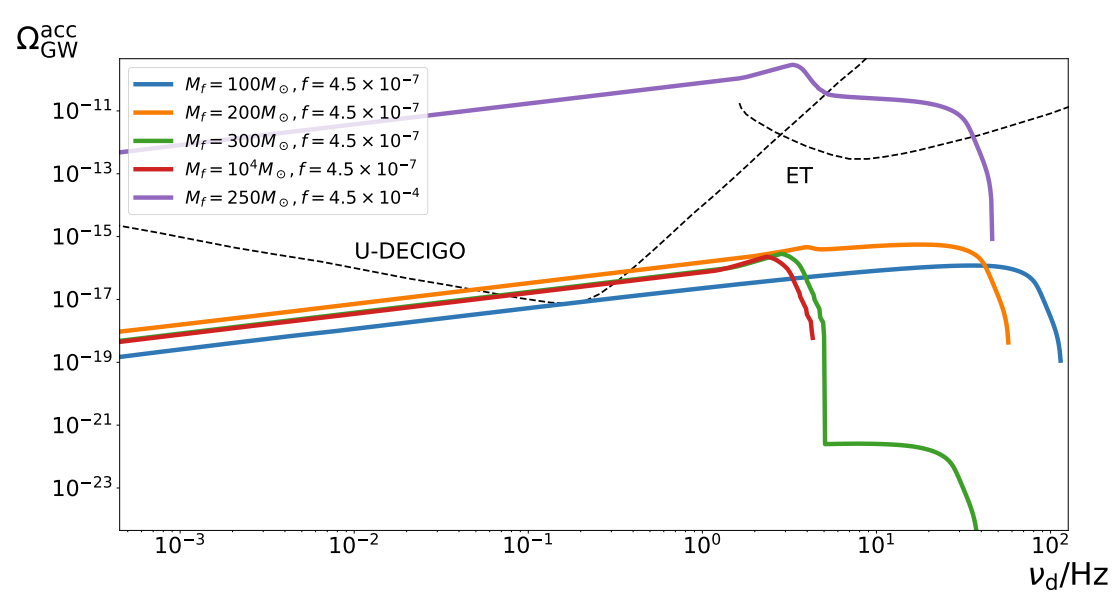
Examples of \(\Omega_{GW}\) taking into account mass accretion
Conclusions and discussion
- Peters formula underestimates merger rate of large PBHs
- GWB spectrum for mergers of PBH with \(M>10^5M_\odot\) develops an extra peak
- If future missions do not see such a background, the fraction of dark matter in PBHs is constrained to \(f < 10^{−6} \text{-}10^{−4}\) within the mass range \(10\text{-}10^9M_\odot\)
- Mass accretion at \(z\sim 10\) could significantly affect GWB from PBH mergers
- Some assumptions in this work: monochromatic PBHs, no PBH clustering, simple accretion models...
deck
By Heling Deng
