Future State Maximisation: A Survey of
Henry Charlesworth (H.Charlesworth.1@warwick.ac.uk)
Future State Maximisation Workshop, University of Graz, 17th Dec 2019
Related Ideas and an Application to Collective Motion
About me
- Until recently I was a PhD student based in the Centre for Complexity Science, University of Warwick.
- Supervised by Professor Matthew Turner (Physics, Centre for Complexity Science)
- Now, still at Warwick, but a postdoc in Warwick Manufacturing Group's Data Science group (deep reinforcement learning research), working with Progessor Giovanni Montana
Overview of this talk
- Philosophy/ motivation behind FSM
2. Introduction to the empowerment framework
- differences with causal entropic forces
- why I prefer it!
- relation to "intrinsic motivations" in psychology
3. Ideas related to FSM in the reinforcement learning literature
4. My PhD research - FSM applied to collective motion
5. Conclusions
Philosophy/ motivation behind FSM
- Useful to think about the underlying principles separately from any particular quantitative frameworks based on them (e.g. causual entropic forces, empowerment)
- Layman's summary: "Taking all else to be equal, aim to keep your options open as much as possible".
- Maximise the amount of control you have over the potential states that you are able to access in the future.
- Rationale is that in an uncertain world, this puts you in a position where you are best prepared to deal with the widest range of future scenarios you may end up encountering.
FSM - high-level examples
- Owning a car vs. not owning a car
- Going to university
- Aiming to be healthy rather than sick
- Aiming to be rich rather than poor
- A concept introduced in the psychology literature to explain the incentive for behaviour which does not provide an immediate or obviously quantifiable benefit to the decision making agent.
- e.g. exploring novel environments, play, accumulating knowledge
Connection to "Intrinsic Motivation"
- White (1959) argued that intrinsically motivated behaviour was necessary for an agent to gain the competence necessary to achieve mastery over its environment - and hence for autonomy.
- Can view FSM as a task-independent intrinsic motivation that should encourage an agent to maximise the control over what it is able to do - hence "achieving mastery" over its environment
- In principle, achieving "mastery" over your environment in terms of maximising the control you have over the future things that you can do should naturally lead to: developing re-usable skills, obtaining knowledge about how your environment works, etc.
- Could also be useful as a proxy to evolutionary fitness in many situations. Achieving more control over what it is potentially able to do is almost always beneficial.
Philosophy/ motivation behind FSM
Connection to "Intrinsic Motivation"
How can FSM be useful?
- If you accept this is often a sensible principle to follow, we might expect behaviours/heuristics to have evolved that make it seem like an organism is applying FSM.
Could be useful in explaining/understanding
certain animal behaviours.
- Could also be used to generate behaviour for artificially intelligent agents.
Quantifying FSM
- "Causal Entropic Forces" (Approach based on thermodynamics)
- "Empowerment" (Information theoretic approach)
[1] "Empowerment: A Universal Agent-Centric Measure of Control" - Klyubin et al. 2005
[2] "Causal Entropic Forces" - Wissner-Gross and Freer, 2013
Empowerment
- Formulates a measure of the amount of control an agent has over it's future in the language of information theory.
I(X;Y) = H(Y) - H(Y|X) = H(X) - H(X|Y)
- Mutual information - measures how much information one variable tells you about the other:
- Channel capacity:
C(X \to Y) = \max_{\mathbb{P}(x)} I(X;Y)
Empowerment
- Consider an agent making decisions at discrete time steps. Let \( \mathcal{A} \) be the set of actions it can take, and \( \mathcal{S} \) be the set of possible states its "sensors" can be in.
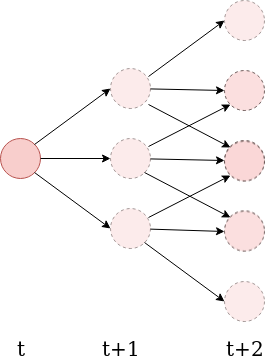
- Define the n-step empowerment to be the channel capacity between the agent's available action sequences, and the possible states of its sensors at a later time \(t+n\):
\mathfrak{E}_n = C(A_t^n \to S_{t+n}) = \max_{\mathbb{P}(a_t^n)} I(A_t^n ; S_{t+n})
- Explicitly measures how much an agent's actions are capable of influencing the potential states its sensors can be in a later time.
Empowerment vs. CEF
- Empowerment explicitly considers the control the agent has - in terms of how much the agent's actions effect the future states it can perceive.
defined entirely in terms of the agent's "perception-action" loop
- Causal entropic forces - calculate a path integral over all possible future trajectories
S_c(\mathbf{X}, \tau) = -\int_{\mathbf{x}(t)} \mathbb{P}[\mathbf{x}(t) | \mathbf{x}(0)] \log \mathbb{P}[\mathbf{x}(t) | \mathbf{x}(0)] \mathcal{D}\mathbf{x}(t)
- Implicitly requires a kind of "default model" for how the system will evolve/how the agent will act in the absence of the causal entropic force.
\mathfrak{E}_n = C(A_t^n \to S_{t+n}) = \max_{\mathbb{P}(a_t^n)} I(A_t^n ; S_{t+n})
Empowerment vs. CEF
- Agents moving according to causal entropic forces should be naturally drawn towards sources of randomness that they have no control over.
- Empowerment (arguably) easier to calculate - recent techniques make it possible to approximate mutual information between high dimensional inputs.
(noisy TV problem - originally used as an example of where prediction based novelty algorithms fail - also applicable to CEF)
Goal-conditioned Reinforcement Learning (many papers)
Standard reinforcement learning paradigm: Markov decision processes
\(s_0, a_1, r_1, s_1, a_2, r_2, \dots\)
states
actions
rewards
Learn a policy \(\pi(a | s) \) to maximise expected return:
\mathbb{E}[\sum_{t=0}^{\infty} \gamma^t r_t | s_0 = s]
Goal-conditioned RL: learn a policy conditioned on a goal g:
\pi(a|s, g)
\gamma \in [0,1)
-
Consider the case where the set of goals is the same as the set of states the system can be in, and take the reward function to be e.g. the distance between the state s and the goal g, or an indicator function for if the goal has been achieved.
- In this case you are trying to learn (ideally) a policy \( \pi(a| s_i, s_f)\) that allows you to get between any two states \(s_i\) and \(s_f\).
Ideas related to FSM in Reinforcement Learning
"Skew-fit: State-Covering Self-Supervised Reinforcement Learning" - Pong et al. 2019
Ideas related to FSM in Reinforcement Learning
- Goal-conditioned RL where the aim is to explicitly maximise the coverage of the state space that can be reached - philosophy is very closely related to FSM.
https://sites.google.com/view/skew-fit
- Maximises an objective: \(I(S;G) = H(G) - H(G|S)\)
set diverse goals
Make sure you can actually
achieve the goal from each state
- Similar to maximising empowerment - potential advantage here is that learning a goal-conditioned policy actually tells you how to do everything as well.
- Equivalently: \(I(S;G) = H(S) - H(S|G)\)
Maximise coverage of state space
Be able to control where the policy
goes by giving it a goal
"Variational Information Maximisation for Intrinsically Motivated Reinforcement Learning" - Mohamed and Rezende (2015)
- Use a variational bound on the mutual information to estimate the empowerment in examples with high-dimensional input spaces (pixels of images)
- Use the empowerment as an intrinsic reward signal and apply reinforcement learning so that the agents learn to maximise their empowerment in some simple environments.
Ideas related to FSM in Reinforcement Learning
How can FSM be useful in understanding collective motion?
"Intrinsically Motivated Collective Motion"
"Intrinsically Motivated Collective Motion" - PNAS 2019 - https://www.pnas.org/content/116/31/15362 (Charlesworth and Turner)
What is Collective Motion?
- Coordinated motion of many individuals all moving according to the same rules.
- Occurs all over the place in nature at many different scales - flocks of birds, schools of fish, bacterial colonies, herds of sheep etc.
Why Should we be Interested?
Applications
- Animal conservation
- Crowd Management
- Computer Generated Images
- Building decentralised systems made up of many individually simple, interacting components - e.g. swarm robotics.
- We are scientists - it's a fundamentally interesting phenomenon to understand!
Existing Collective Motion Models
- Often only include local interactions - do not account for long-ranged interactions, like vision.
- Tend to lack low-level explanatory power - the models are essentially empirical in that they have things like co-alignment and cohesion hard-wired into them.
Example: Vicsek Model
T. Vicsek et al., Phys. Rev. Lett. 75, 1226 (1995).
R
\mathbf{v}_i(t+1) = \langle \mathbf{v}_k(t) \rangle_{|\mathbf{r}_k-\mathbf{r}_i| < R} + \eta(t)
\mathbf{r}_i(t+1) = \mathbf{r}_i(t) + \mathbf{v}_i(t)
Our approach
- Based purely on a simple, low-level motivational principle - FSM.
- No built in alignment/cohesive interactions - these things emerge spontaneously.
Our Model
- Consider a group of circular agents equipped with simple visual sensors, moving around on an infinite 2D plane.
Possible Actions:
Visual State
Making a decision
Simulation Result - Small flock
Leads to robust collective motion!
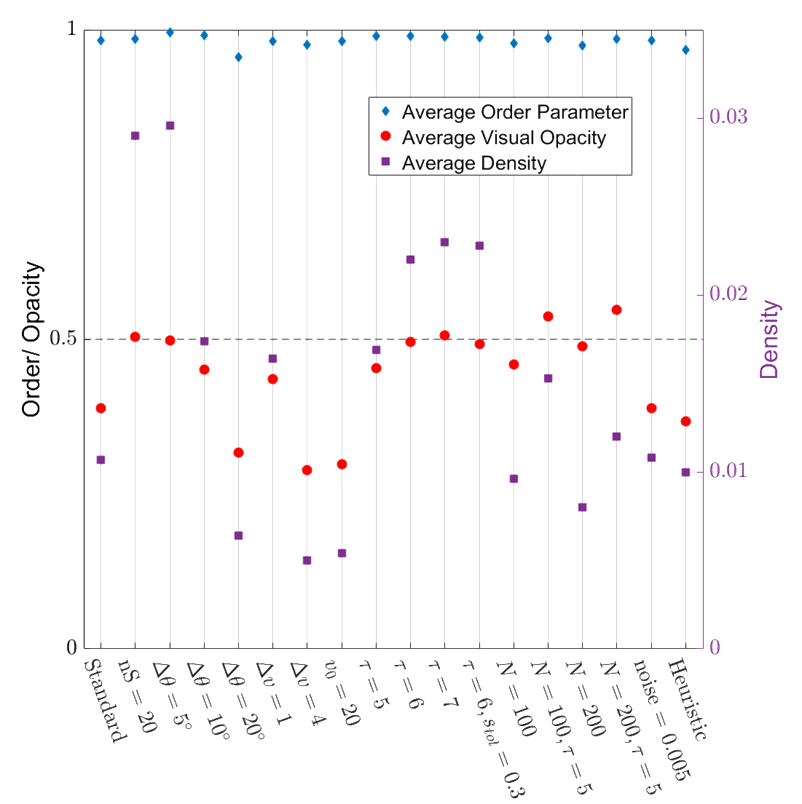
- Very highly ordered collective motion. (Average order parameter ~ 0.98)
- Density is well regulated, flock is marginally opaque.
- These properties are robust over variations in the model parameters!
\phi = \frac{1}{N} |\sum_i \mathbf{\hat{v}}_i |
Order Parameter:
Also: Scale Free Correlations
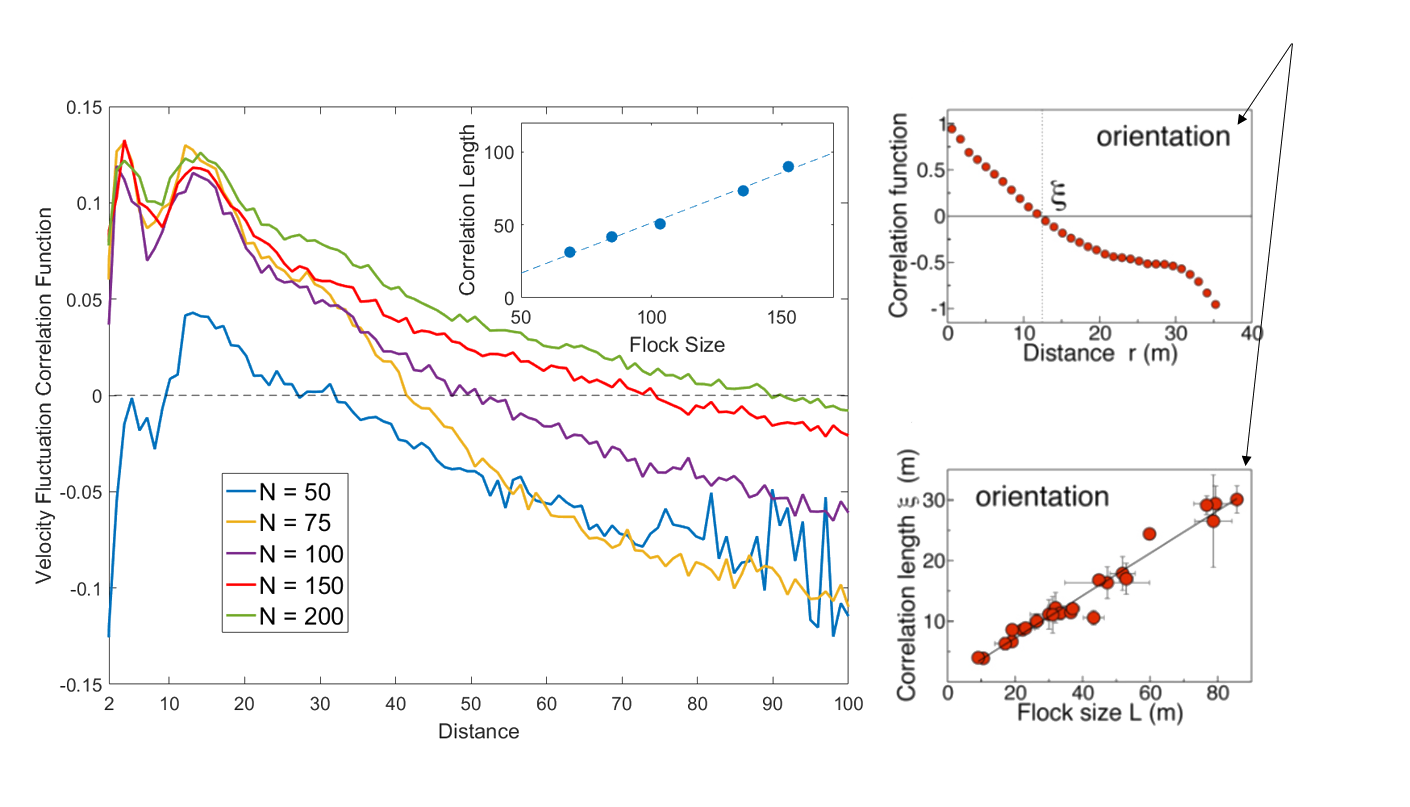
Real starling data (Cavagna et al. 2010)
Data from model
- Scale free correlations mean an enhanced global response to environmental perturbations!
\mathbf{u_i} = \mathbf{v_i} - \langle \mathbf{v} \rangle
correlation function:
C(r) = \langle \mathbf{u}_i(0) . \mathbf{u}_j(|r|) \rangle
velocity fluctuation
Continuous version of the model
- Would be nice to not have to break the agents' visual fields into an arbitary number of sensors.
- Calculating the mutual information (and hence empowerment) for continuous random variables is difficult - need to take a different approach.
Continuous version of the model
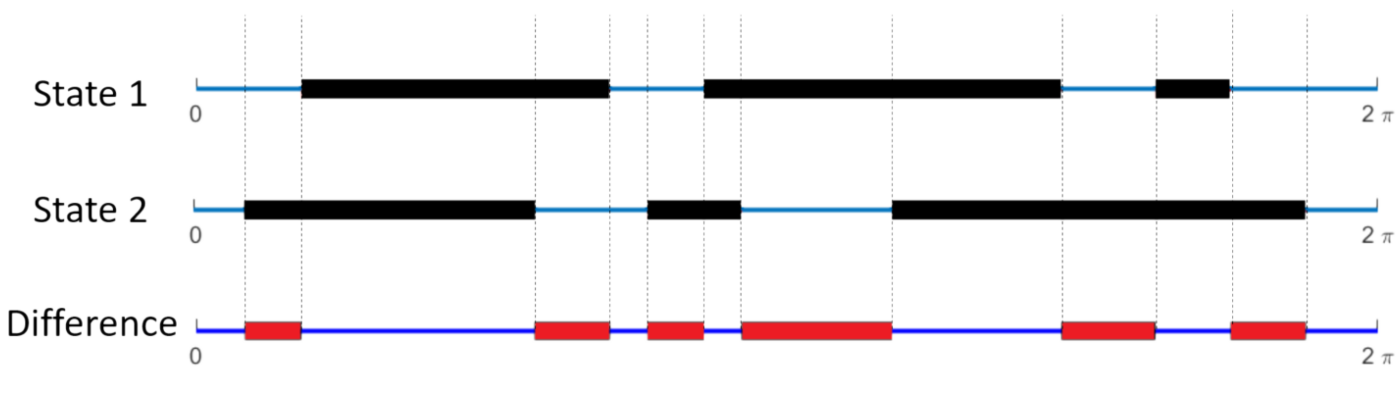
- Let \(f(\theta)\) to be 1 if angle \(\theta\) is occupied by the projection of another agent, or 0 otherwise
- Define the "difference" between two visual states i and j to be:
d_{ij} = \frac{1}{2\pi} \int_0^{2\pi} [f_i(\theta)(1-f_j(\theta)) + f_j(\theta)(1-f_i(\theta))]d\theta
- This is simply the fraction of the angular interval \([0, 2\pi)\) where they are different.
Continuous version of the model
W_{\alpha} = \frac{1}{n_{\alpha}} \sum_{i=1}^{n_{\alpha}} \sum_{j=1}^{n_{\alpha}} d_{ij}
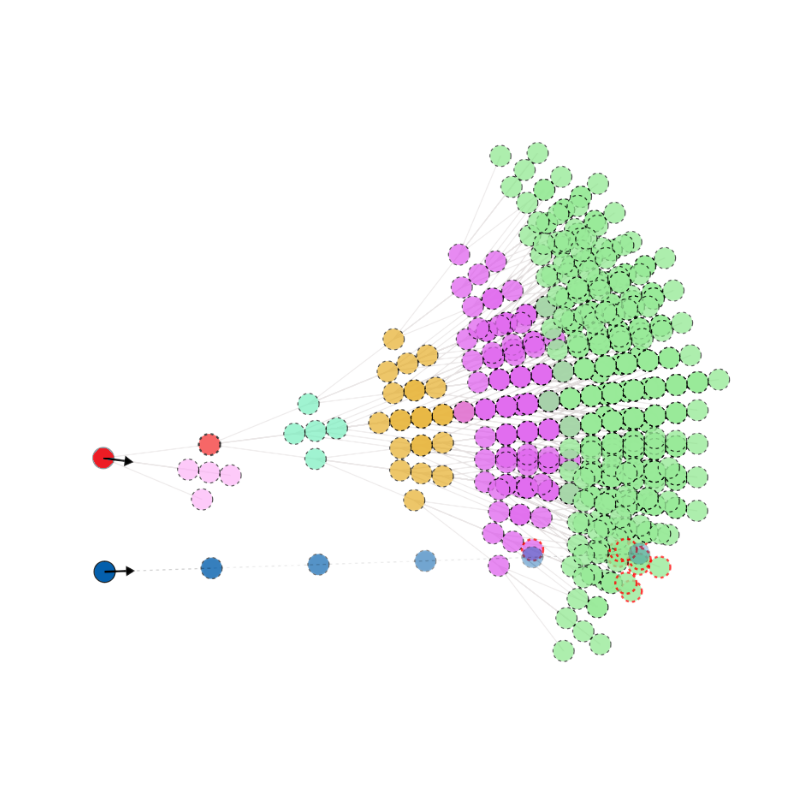
branch \(\alpha\)
For each initial move, \( \alpha \), define a weight as follows:
- Rather than counting the number of distinct visual states on each branch, this weights every possible future state by its average difference between all other states on the same branch.
- Underlying philosophy of FSM remains the same.
Result with a larger flock - remarkably rich emergent dynamics
Can we do this without a full search of future
- This algorithm is very computationally expensive. Can we generate a heuristic that acts to mimic this behaviour?
- Train a neural network on trajectories generated by the FSM algorithm to learn which actions it takes, given only the currently available visual information (i.e. no modelling of future trajectories).
states?
Visualisation of the neural network
previous visual sensor input
current visual sensor input
hidden layers of neurons
output: predicted probability of action
non-linear activation function: f(Aw+b)
How does it do?
Some other things you can do
Making the swarm turn
Guiding the swarm to
follow a trajectory
A bit of fun: FSM at different scales:
Conclusions
- Can separate the philosophy that underlies FSM from particular quantitative frameworks based on it - view it as an intrinsic motivation for behaviour.
- Lots of different ideas in a variety of fields that are at least somewhat related to FSM.
- Using a vision-based FSM model spontaneously leads to organised collective motion - collective motion emerges directly from the low-level principe.
Future State Maximisation Workshop
By Henry Charlesworth
