Flexible Image modelling for deblending and strong gravitational lensing

Rémy Joseph
Stockholm, Oct. 15 2021
Collaborators: Peter Melchior, Fred Moolekamp, Frederic Courbin (EPFL, SW), Jean-Luc Starck (CEA, FR), Aymeric Galan (EPFL), Austin Peel, Martin Millon (EPFL), François Lanusse (CNRS, FR), Jiaxuan Li (PKU), Jenny Greene, Johnny Greco (OSU).






MuSCADeT/SCARLET
- Colour-based: each band is a linear combination of monochromatic components
F435w: \(I_2\)
F606w: \(I_1\)
F814w: \(I_0\)
$$I_j = H_j \sum_i a_{j,i}m_i + N_j$$
$$m_0$$
$$m_1$$
$$I$$


Functional decompositions:
The Starlet transfrom
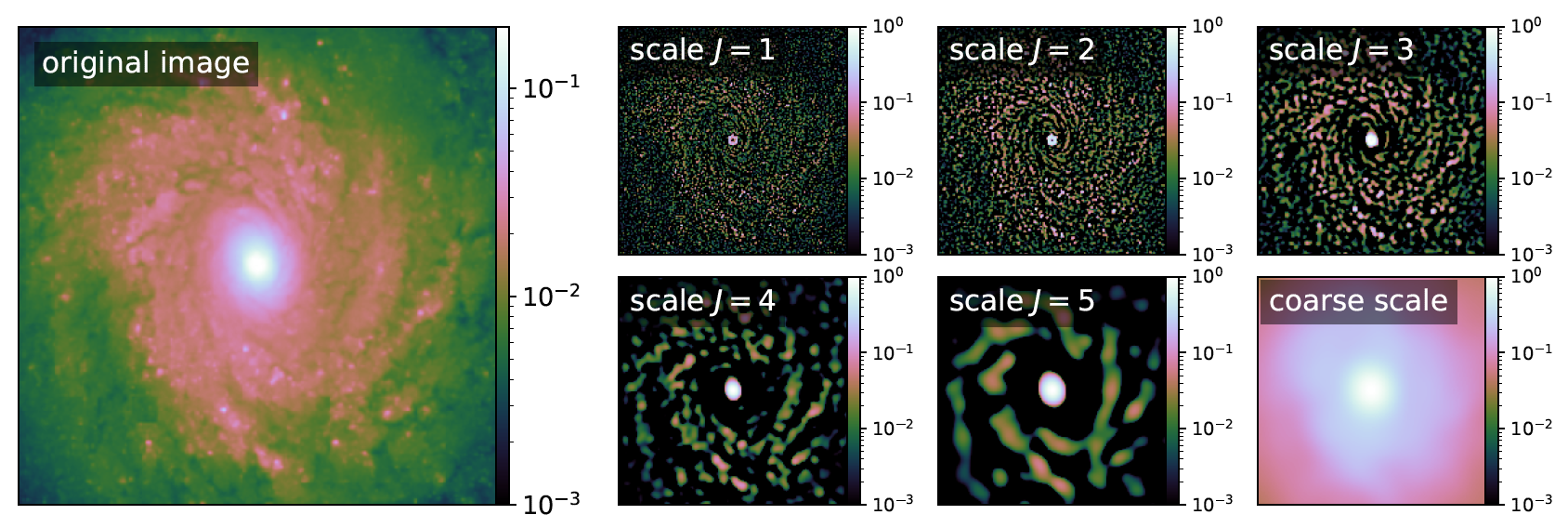
Starlet coefficients
- Multiscale transformation
- Decomposition in B-splines at different spatial scales
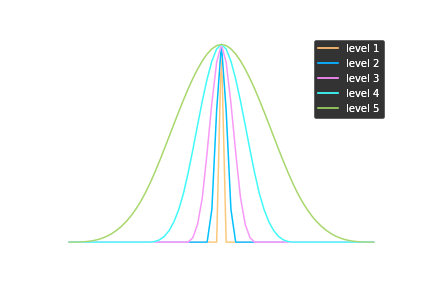
Starlet basis set
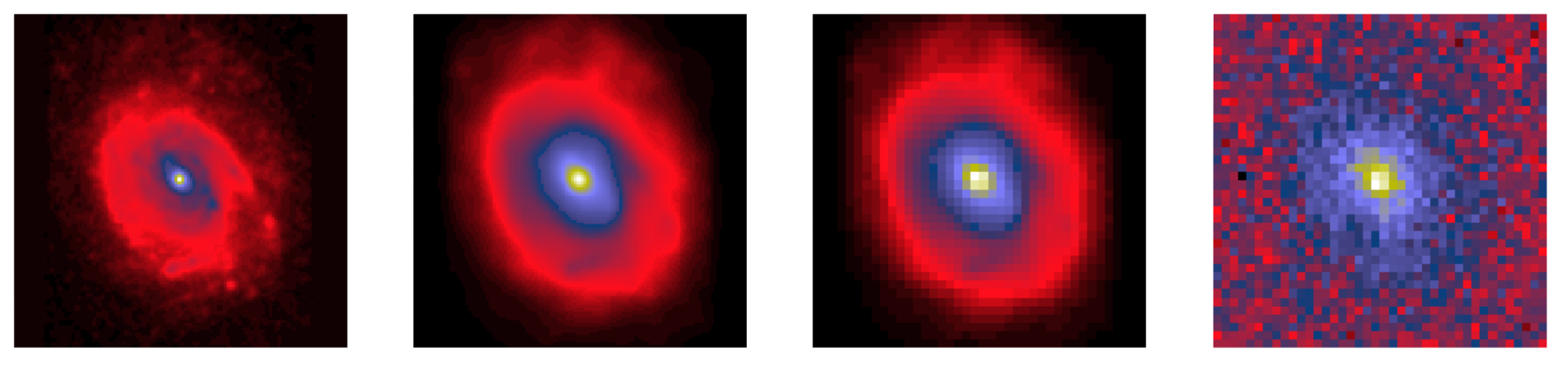
Low Surface Brightness Galaxies
On going work with Jiaxuan Li, Johnny Greco & Jenny Greene




HSC image
image-model
LSB model
Residuals
Reconstruction of strongly lensed source


Strong gravitational lens searches

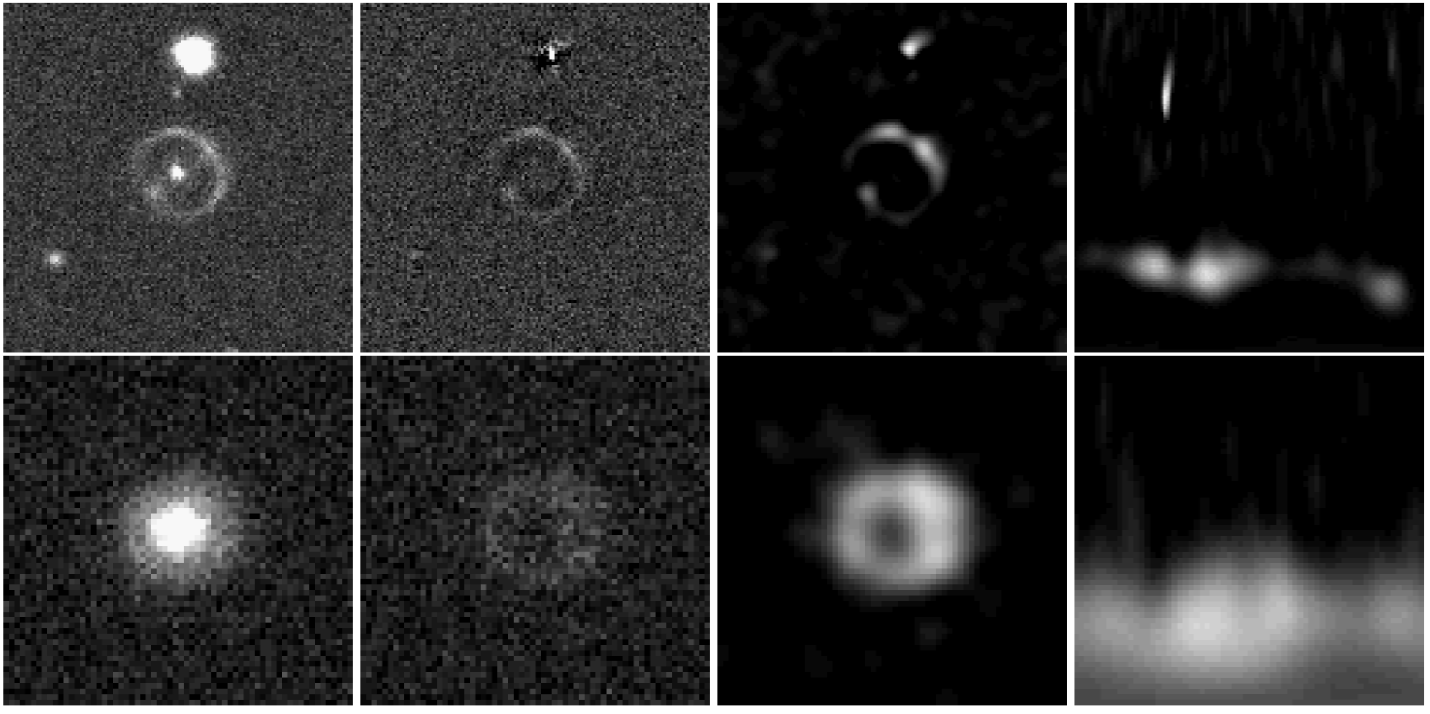
Automated searches rely heavily on ML to find strong lens candidates.
- ML finders are only as good as their training. e.g. Rojas et al. injects strongly lensed features in DES images to build a training set.
- ML finders identify ~1000s of candidates.
- Deblending for lens finding to help the finders (humans or not)
Modelling astro images for
Deblending
Galaxy light profile
Telescope refraction (convolution)
Instrument acquisition (pixelation)
Instrumental noise
Constraints on starlet coefficients
Is achieved by reconstructing sparse fields in starlets:
\( \tilde{S} = \underset{S}{argmin}\) \( \frac{1}{2}||I-HA\Phi S||^2_2 \) \(+\) \(\lambda||S||_1\) \(+\) \(\mathcal{i}_+(\Phi S) \)
Likelihood Sparsity Positivity
(smoothness constraint)
MuSCADeT: Joseph et al. 2016 (arxiv:1603.00473)
$$I_j = R*P_j * \sum_i a_{j,i}\Phi s_i + N_j, \qquad m_i = \Phi s_i$$




Functional decompositions:
The Starlet transfrom
Illustration: Detection in crowded fields
Credit: Fred Moolekamp
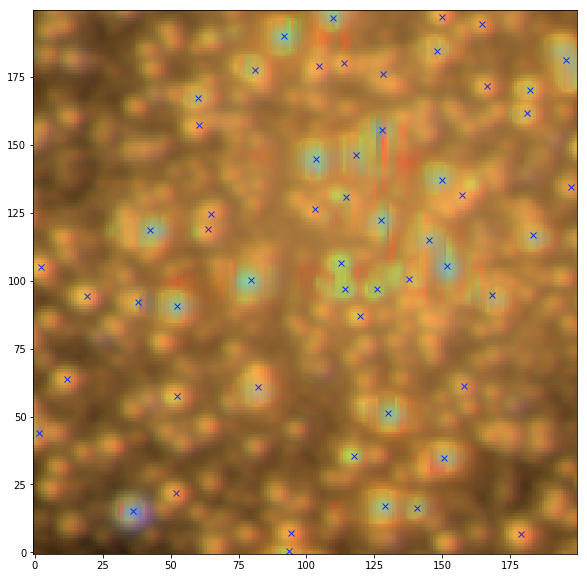
NGC 6569
Sep detection
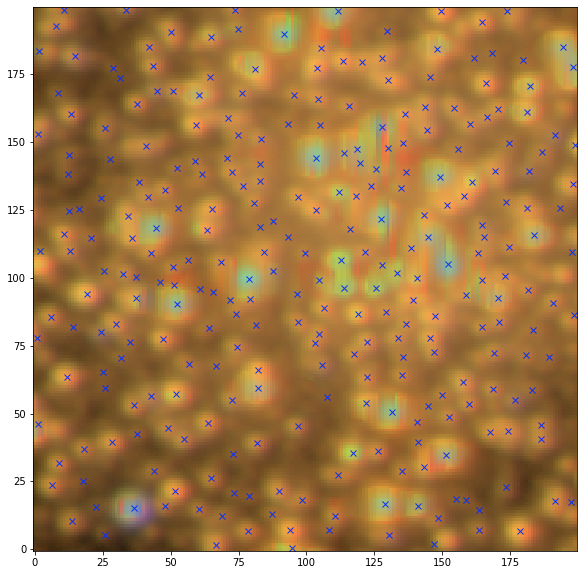
NGC 6569
Starlet+Sep detection

NGC 6569
Starlet level 1
$$I_j = R*P_j * \sum_{i,n} a_{j,i,n}m_{i,n}$$
PixelCNN as a prox
In scarlet
- Scarlet is flexible to the kind of constraints we can impose on morphology. We are now implementing priors PixelCNN Lanusse et al. 2019:
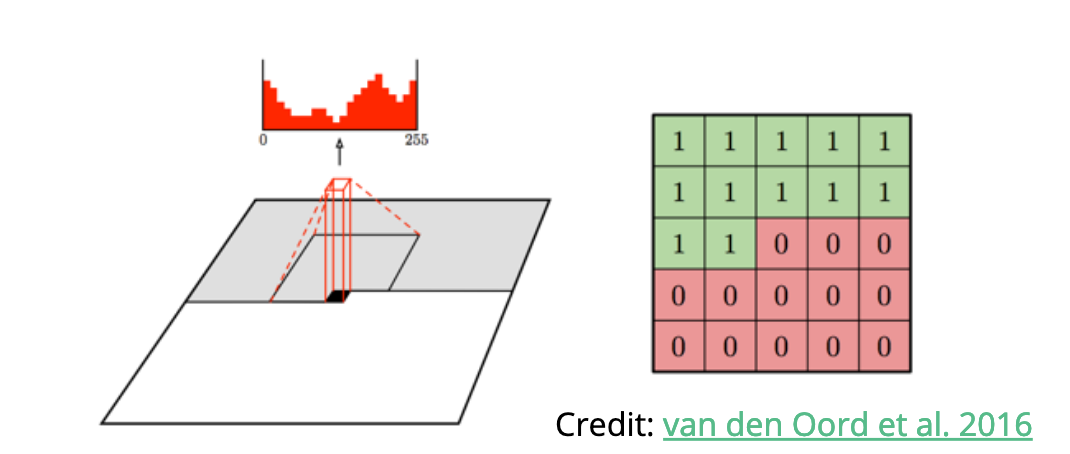
$$p(m) = \prod_k p(m_k|m_{k-1}, ..., s_0) $$
\( \tilde{M} = \underset{M}{argmin}\) \( \frac{1}{2}||I-HAM||^2_2 \) \(+\) \(\sum_i p(m_i)\)
Copy of Snova talk
By herjy
Copy of Snova talk
- 296



