Field-level inference from galaxy surveys

Context

🫁

🚬

☢️

🚗

https://www.cancer-environnement.fr/fiches/cancers/cancer-du-poumon/

$$\mathbb O(🤒 \mid ➕) = \operatorname{BF}(➕)\; \mathbb O(🤒) = \frac{\mathbb P(🤒 \mid ➕)}{1-\mathbb P(🤒 \mid ➕)}$$

$$\begin{align*}\mathbb P(🤒 \mid ➕) &= \frac{\operatorname{BF}(➕) \;\mathbb O(🤒)}{1+\operatorname{BF}(➕) \; \mathbb O(🤒)} = \frac{\mathbb P(➕\mid🤒) \mathbb P(🤒)}{\mathbb P(➕\mid😊)\mathbb P(😊)+\mathbb P(➕\mid🤒) \mathbb P(🤒)}\\ &= \frac{\mathbb P(➕\mid🤒) }{\mathbb P(➕)}\mathbb P(🤒)\end{align*}$$

$$\operatorname{BF}(➕) := \frac{\mathbb P(➕\mid🤒)}{\mathbb P(➕\mid😊)}$$

$$\begin{align*}\mathbb P(🤒 \mid ➕) = \frac{\mathbb P(➕\mid🤒) }{\mathbb P(➕)}\mathbb P(🤒)\end{align*}$$

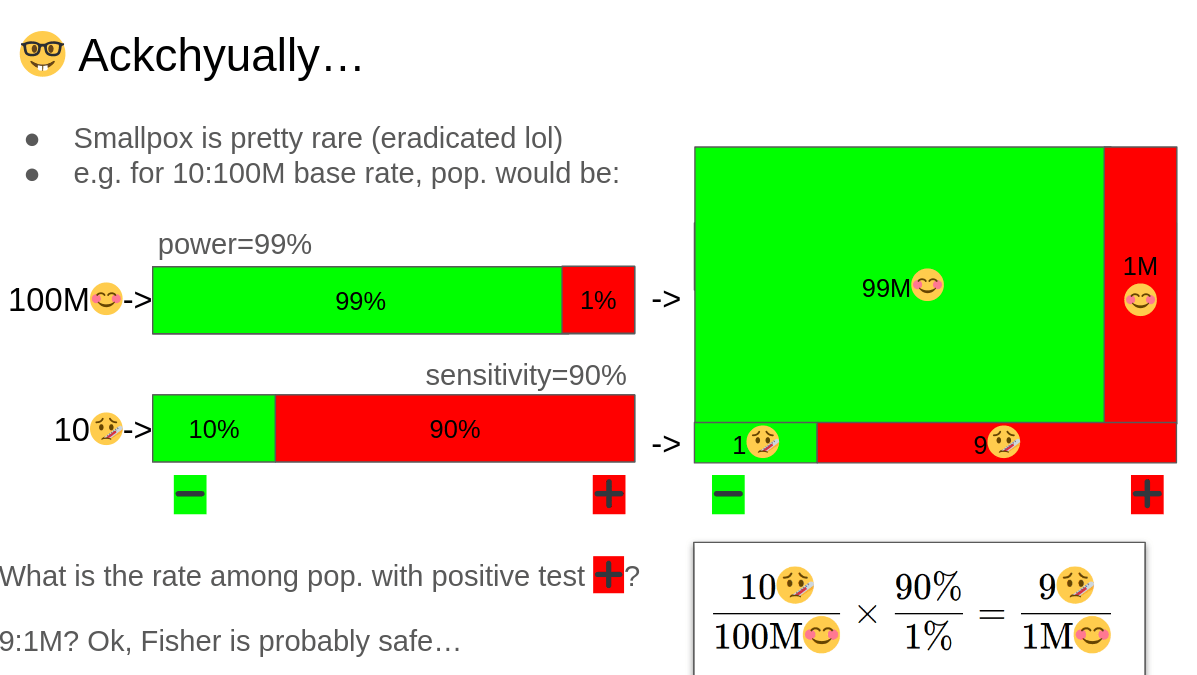
$$\frac{10🤒}{100\text{M}😊}\times \frac{90\%}{1\%}= \frac{9🤒}{1\text{M}😊}$$

$$\log \operatorname{BF}(D)=2.4$$

$$\log\mathbb O(\Lambda\text{CDM})$$

$$\log\mathbb O(w_0 w_a\text{CDM})$$

$$M$$

$$M\mid D$$

$$\frac{9🤒}{1\text{M}😊} = \frac{90\%}{1\%} \times \frac{10🤒}{100\text{M}😊}$$

Invert?

Animate to make it increase

and maybe better down instead?

model: model is defined by its joint proba $p(x, y)$
Bayes Theorem (proba formulation):$$\begin{gather*}p(x \mid y)p(y) = p(x, y) = p(y \mid x)p(x)\\\iff\\\underbrace{p(x \mid y)}_{\text{posterior}} = \frac{\overbrace{p(y \mid x)}^{\text{likelihood}}}{\underbrace{p(y)}_{\text{evidence}}}\underbrace{p(x)}_{\text{prior}}\end{gather*}$$
a priori meaning “from before (observation)”
a posteriori meaning “from after (observation)”
evidence/prior predictive: data evidence, how much the data is evident per se. Alias prior predictive, information on data a priori $$p(y) := \int p(y \mid x) p(x) \mathrm{d} x$$
posterior predictive: information on data a posteriori$$p(y_1 \mid y_0) := \int p(y_1 \mid x) p(x \mid y_0) \mathrm{d} x$$
Bayes factor/likelihood ratio: $\operatorname{BF}(y \mid x_1, x_0):= \frac{p(y_0 \mid x_1)}{p(y_0 \mid x_0)}$

Inference meaning “to transport, propagate (information)”
Bayes Theorem (information formulation):$$H(X \mid Y) = H(Y \mid X) - H(Y) + H(X)$$Moreover$$H(X) - H(X \mid Y) = H(X) + H(Y) - H(X, Y) = I(X;Y) \geq 0$$

$$\mathbb P(X > x \mid H_0)$$

$$\frac{\mathbb P(x\mid H_1)}{\mathbb P(x \mid H_0)}$$

$\theta\mapsto\mathbb P(R(X) \ni \theta \mid \theta)$

$\mathbb P(\theta \in R(X) \mid X)$

$$\inf_{\theta \in \bar \Theta} \mathbb P(R(X) \ni \theta \mid \theta) = 0$$

$\exists \mathbb P_U, \forall \theta \in \bar \Theta, \mathbb P_U(\theta)>0\quad $😎

$$\sqrt n \left( \theta \mid x_{1:n} \mid \theta_0 - \hat \theta(x_{1:n})\mid \theta_0 \right) \xrightarrow[]{\text{TV}} \mathcal N(0, I(\theta_0)^{-1})$$

Modeling

How to compute what we think the universe computes?

(approximately but fastly, please)

Some useful programming tools

NumPyro
- Probabilistic Programming Language (PPL)
- Powered by JAX
- Integrated samplers

JAX
- GPU acceleration
- Just-In-Time (JIT) compilation acceleration
- Automatic vectorization/parallelization
- Automatic differentiation

So JAX in practice?

GPU accelerate
JIT compile
Vectorize/Parallelize
Auto-diff

import jax.numpy as np
# then enjoy

function = jax.jit(function)
# function is so fast now!

gradient = jax.grad(function)
# too bad if you love chain ruling by hand

vfunction = jax.vmap(function)
pfunction = jax.pmap(function)
# for-loops are for-loosers

So NumPyro in practice?

def model():
    z = sample('Z', dist.Normal(0, 1))
    x = sample('X', dist.Normal(z**2, 1))
    return x

render_model(model, render_distributions=True)

x_sample = dict(x=seed(model, 42)())
obs_model = condition(model, x_sample)
logp_fn = lambda z: log_density(obs_model,(),{},{'Z':z})[0]

from jax import jit, vmap, grad
score_vfn = jit(vmap(grad(logp_fn)))

kernel = infer.NUTS(obs_model)
mcmc = infer.MCMC(kernel, num_warmup, num_samples)
mcmc.run(PRGNKey(43))
samples = mcmc.get_samples()

Probabilistic Programming
JAX machinery
Integrated samplers

Now let's build a cosmological model!

Prior on
- cosmology
- initial field
- biases
LPT+PM displacement
RSD displacement
Apply Lagrangian bias
Likelihood of observation

What does it look like?

parameters, huge!
We need inference methods that can scale to high dimensions

6 + \boldsymbol{256^3}

Sampling

Now that you can score...

Always Bayes

p(z \mid x_0) = \frac{p(x_0\mid z)}{p(x_0)} p(z) \propto p(z,x_0)

Random Walk Metropolis-Hasting

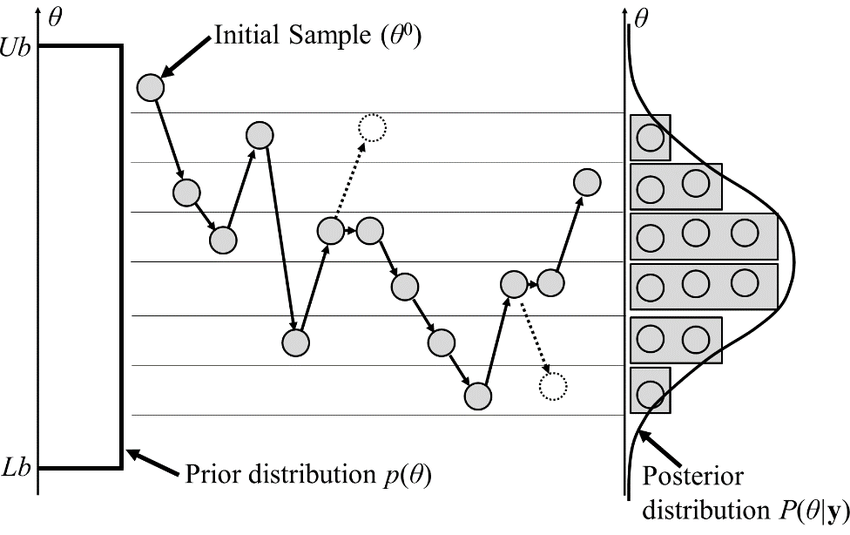
Basic MCMC sampler
Proposal agnostic on the target distribution
- so can't do big steps or will reject a lot, cf. demo

Let's use the score: Langevin dynamics

Score provides local information
- it's the direction of increasing probability
- so let's flow with the (gradient) flow
  $$\quad {\displaystyle {d {z}}=\nabla \log p (z , x_0)dt+{\sqrt {2}}{d {W}}}$$

Not good enough? Let's heat things up

Thanks to score, samples are guided towards high density regions
But when still in low density regions, score helps less...
Idea: smooth target distribution, then slowly decrease smoothing
- procedure called annealing
- can be implemented in several ways

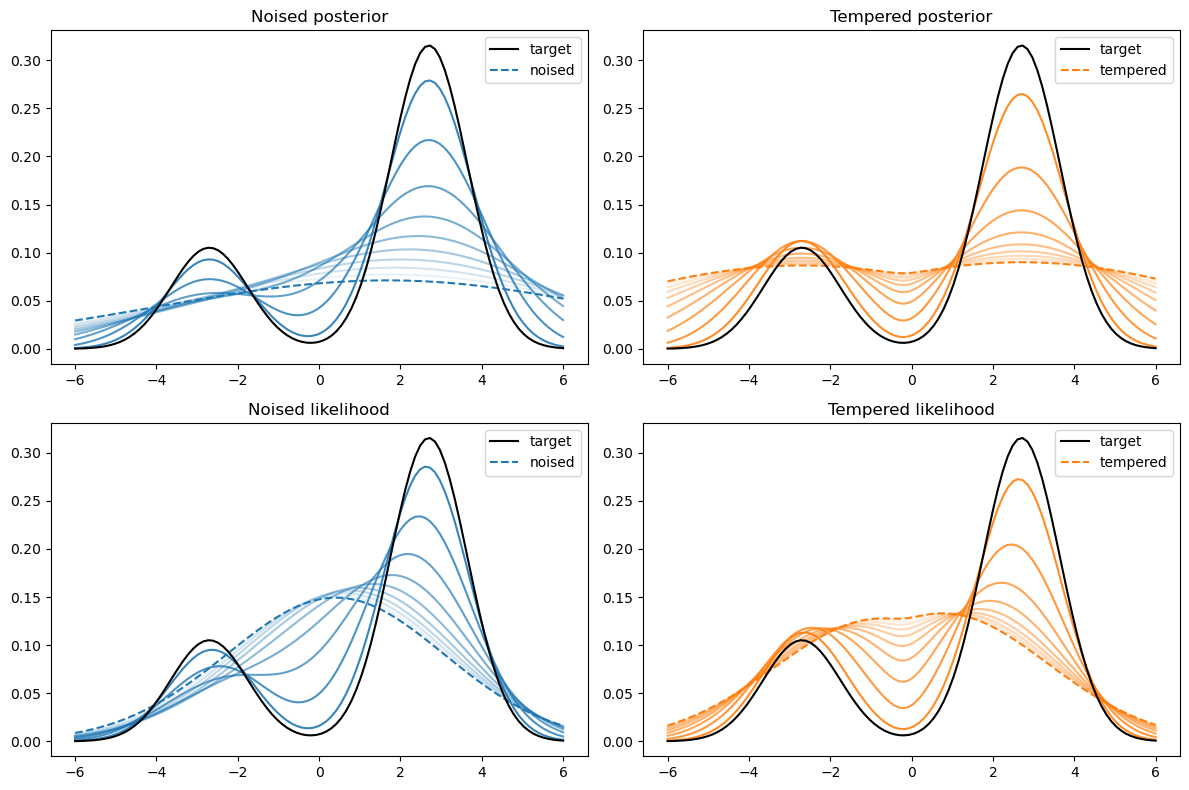
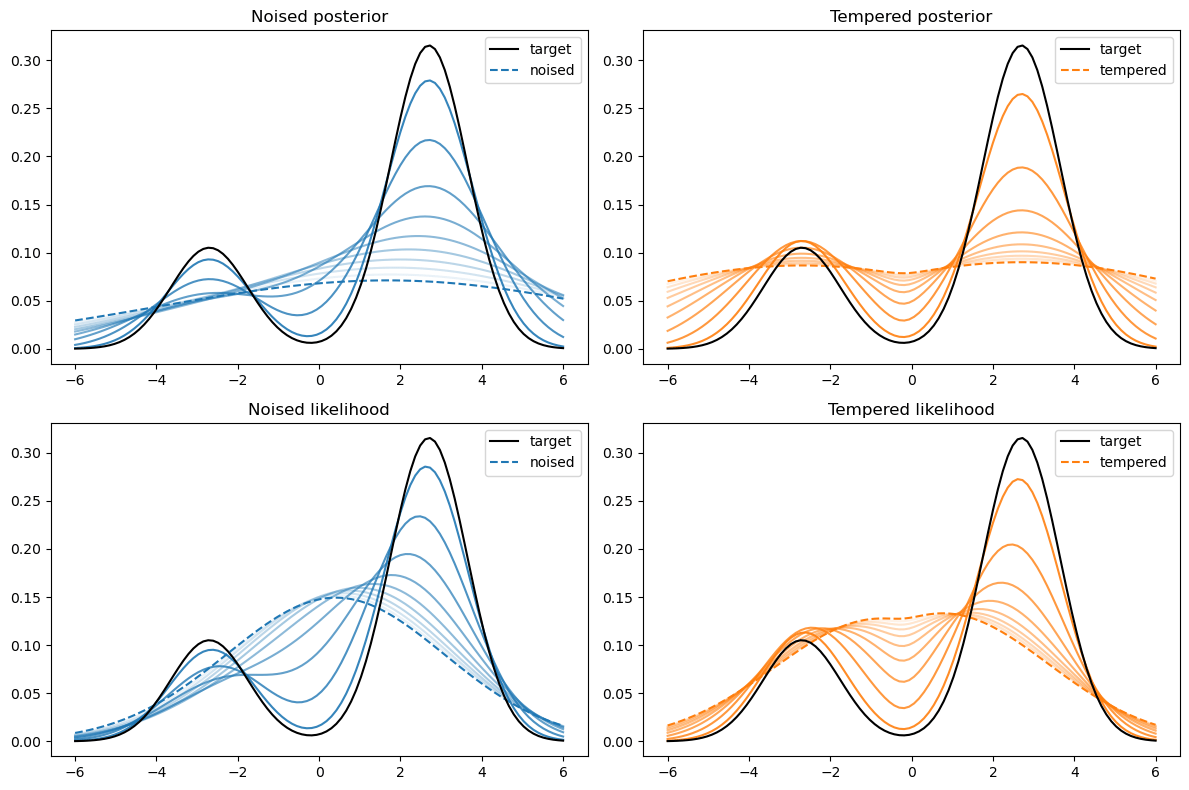
p_\sigma(z,x_0) := p(z,x_0) * \mathcal N(z \mid 0,\sigma^2 I)

p_{T}(z,x_0) := p(x_0 \mid z)^{\frac 1 {T}} p(z)

Not good enough? Let's heat things up

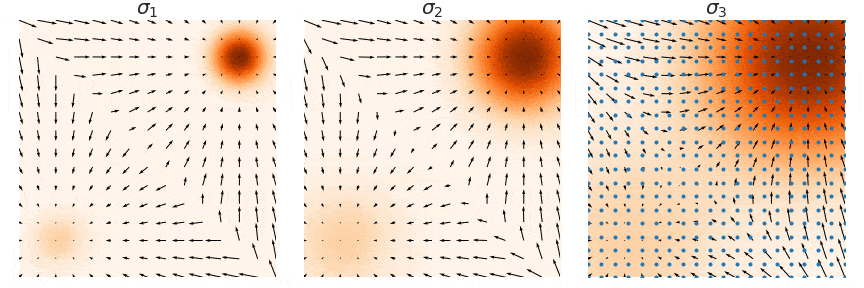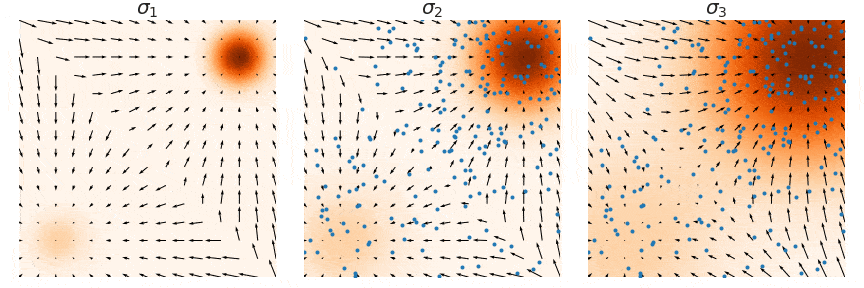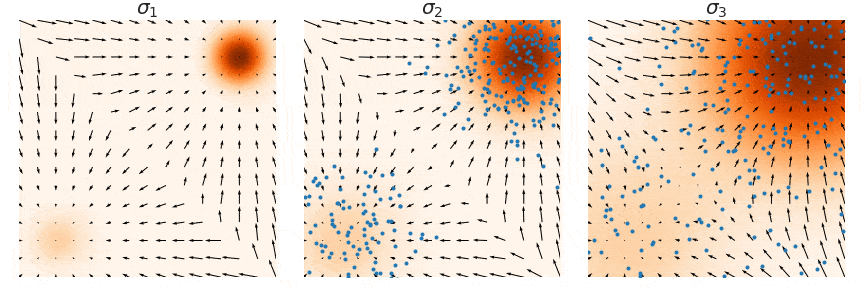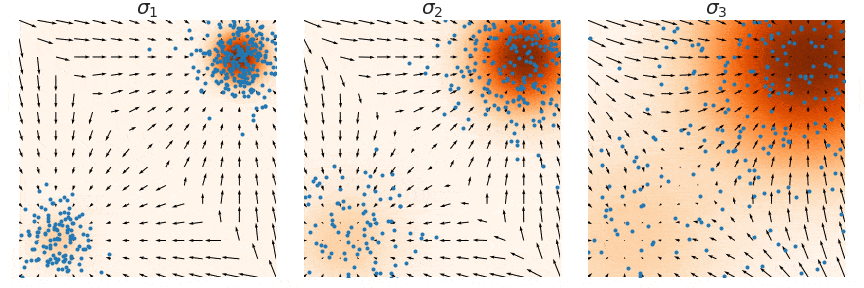
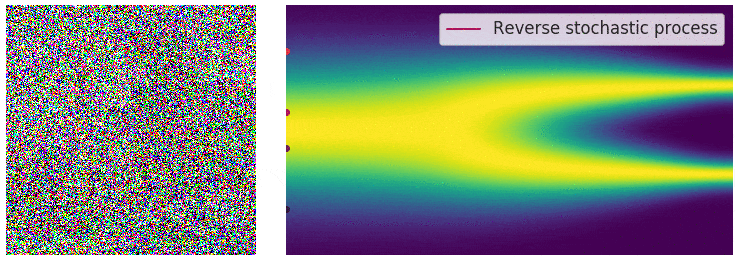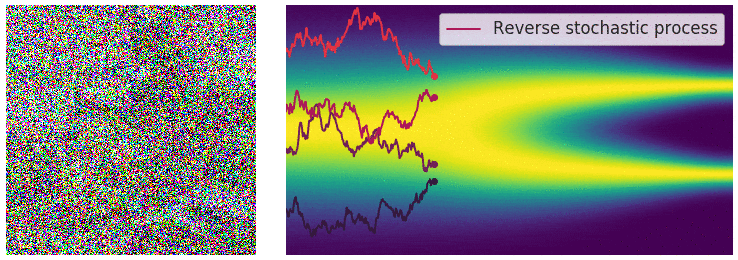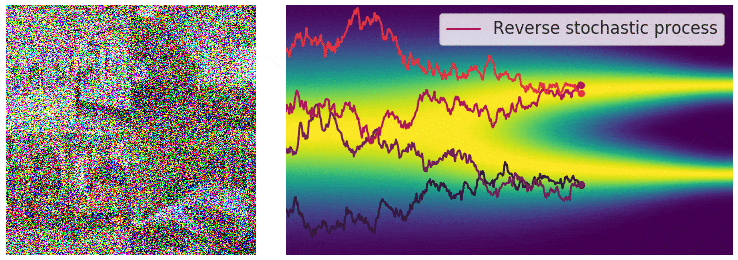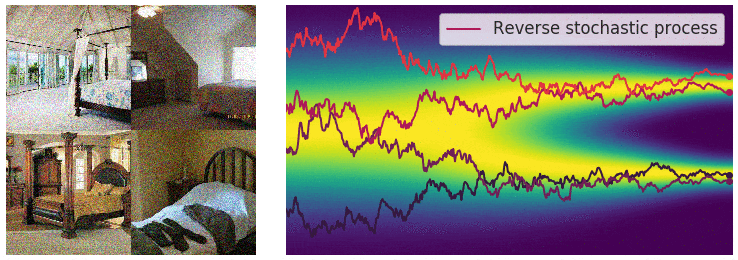
\sigma_1 \quad\quad\quad < \quad\quad\quad \sigma_2 \quad\quad\quad < \quad\quad\quad \sigma_3

Thanks to score, MCs are guided towards high density regions
But when still in low density regions, score helps less...
Idea: smooth target distribution, then slowly decrease smoothing
- procedure called annealing
- can be implemented in several ways
So annealing looks like:

Use the score (again): Hamiltonian Monte Carlo

To travel farther, add inertia
- augment the sampling space by a momentum space
- at each step sample a momentum
- follow the Hamiltonian dynamic
Way less correlated than MH, cf. demo

H(q,p) := -\log p(q \mid x_0) + \frac 1 2 p^2

\dot q = \partial_p H \quad;\quad \dot p = -\partial_q H

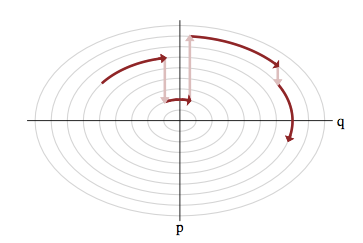
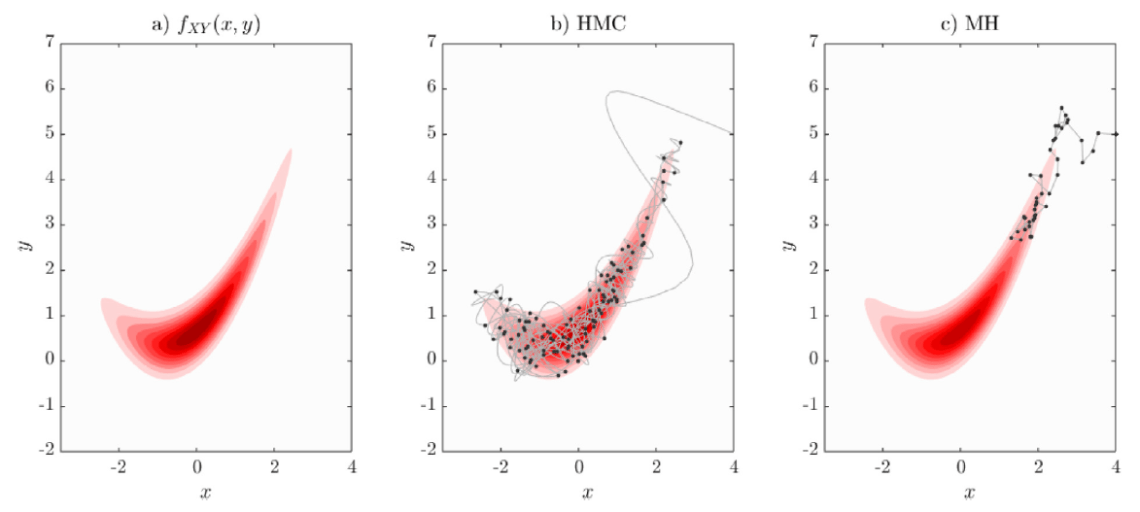
Model Inference

Where model and sampler finally meet

Benchmarking samplers

Plenty of samplers proposed for field-level inference
- Hamiltonian Monte Carlo (HMC)
- HMCGibbs
- No-U-Turn Sampler (🥜)
- MicroCanonical Langevin Monte Carlo (MCLMC)
- Variational self-Boosted Sampling (VBS)
- Metropolis-Adjusted Langevin Algorithm (MALA)
- ...
- currently working on a custom version of "Continuously Annealed Langevin Algorithm"

"Continuously Annealed Langevin Algorithm"

\boldsymbol{z \mid x_0, \Omega_1}

\boldsymbol{z \mid x_0, \Omega_0}

\boldsymbol{z \mid \Omega_1}

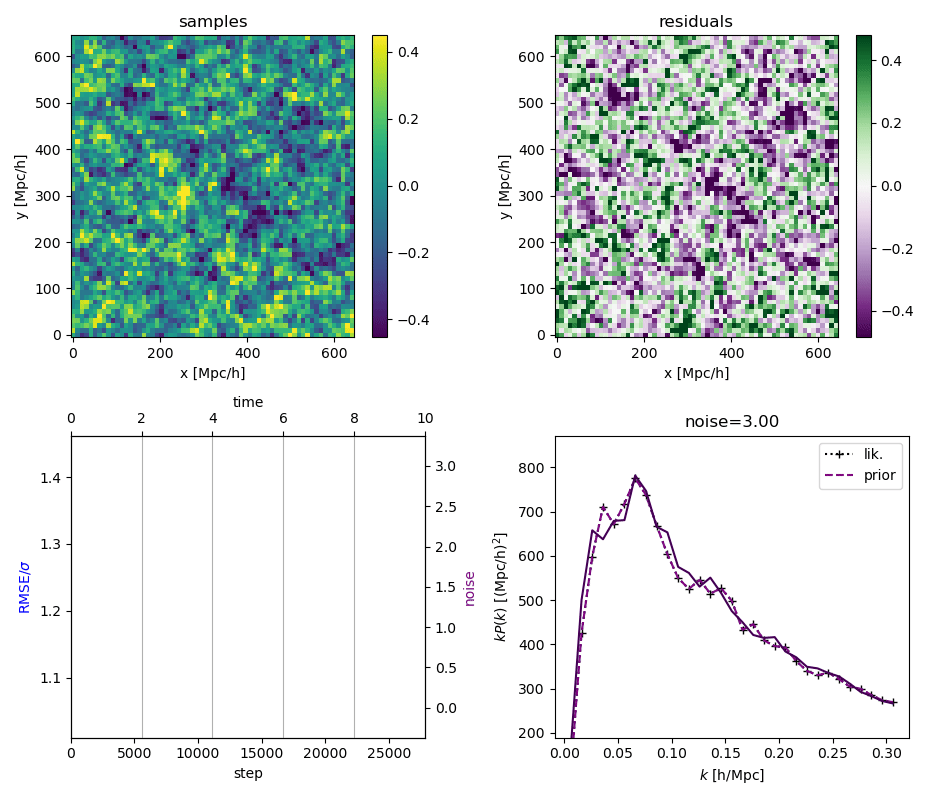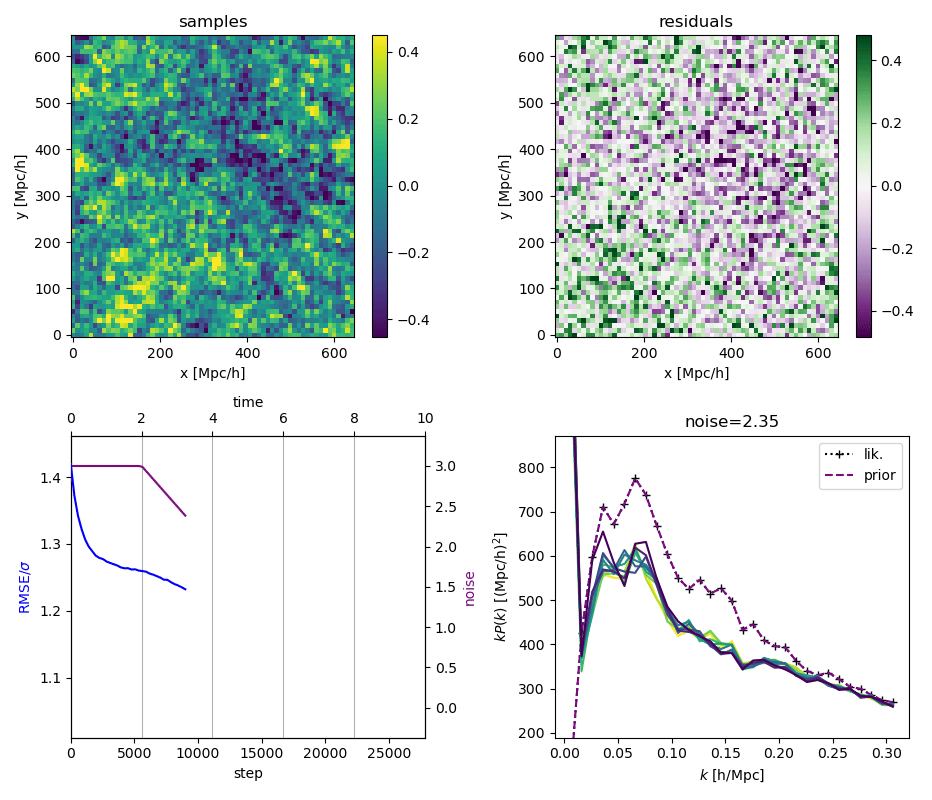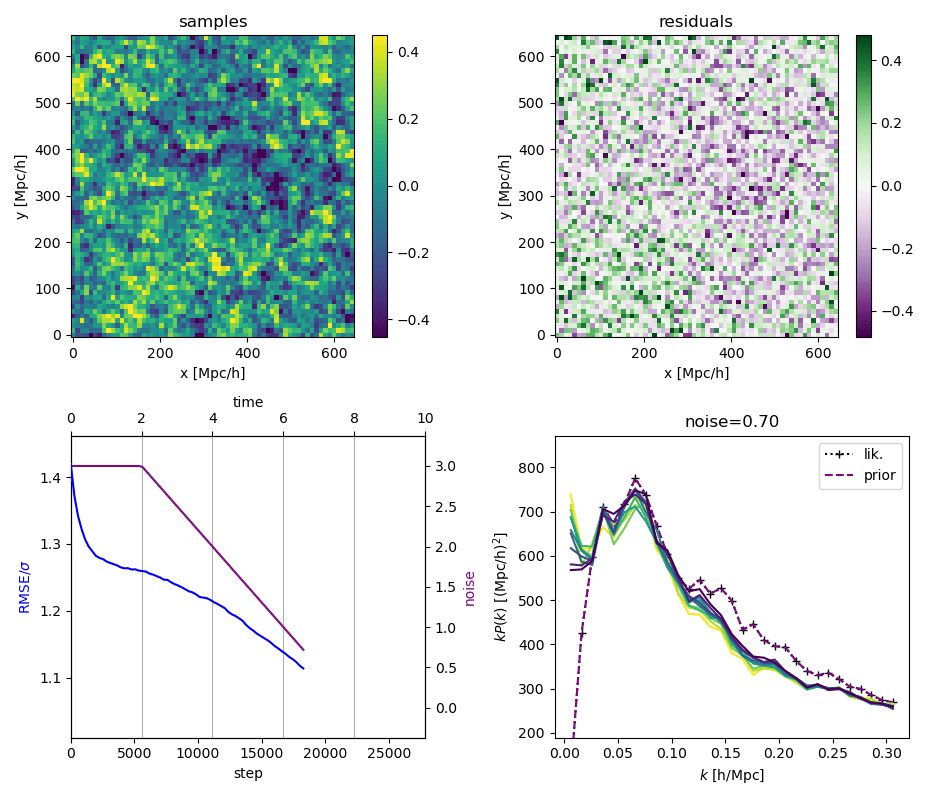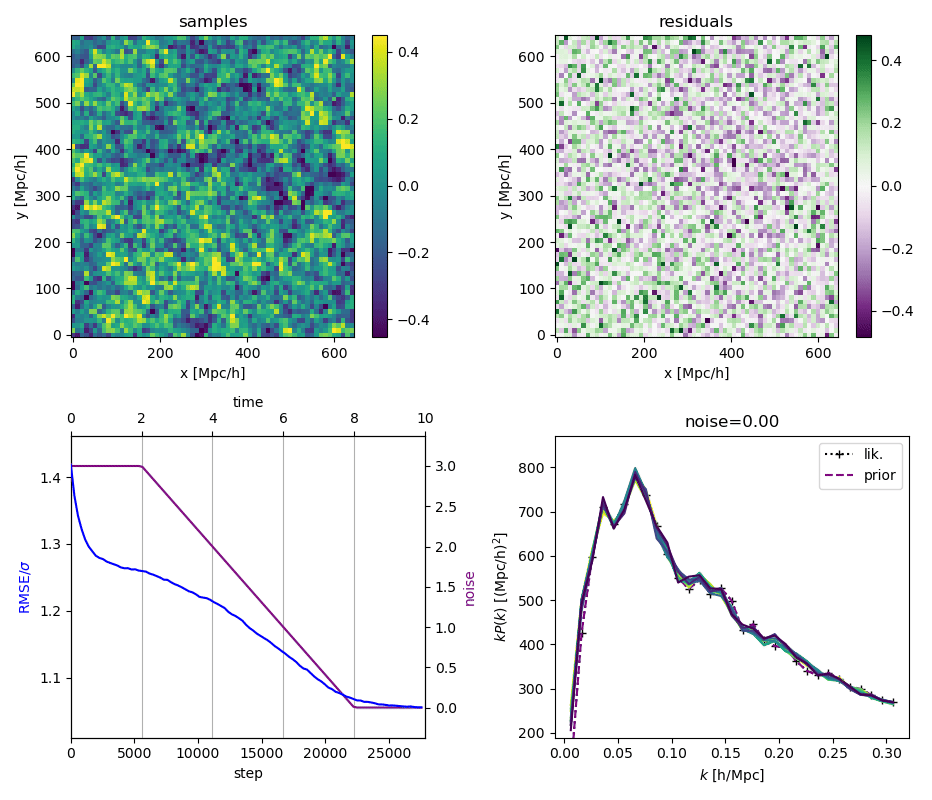
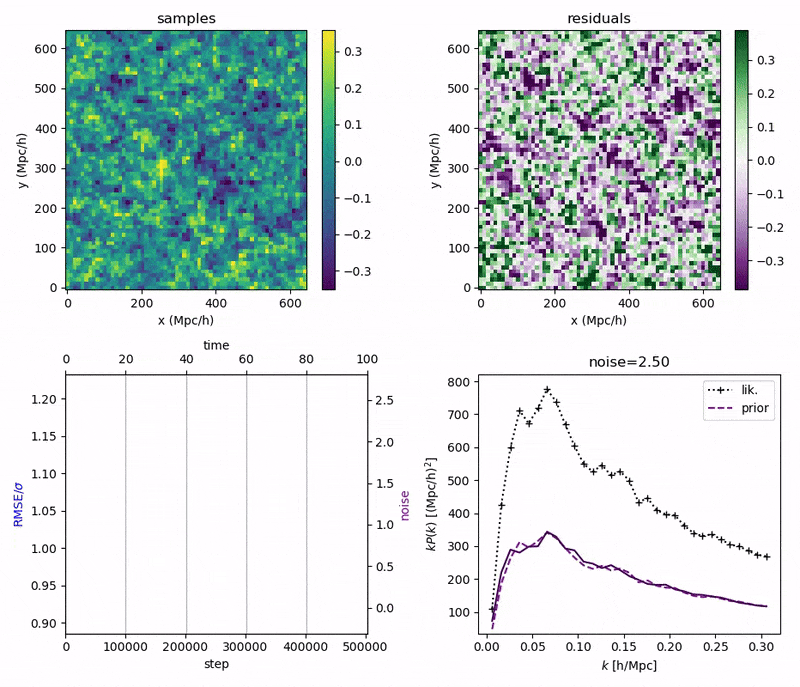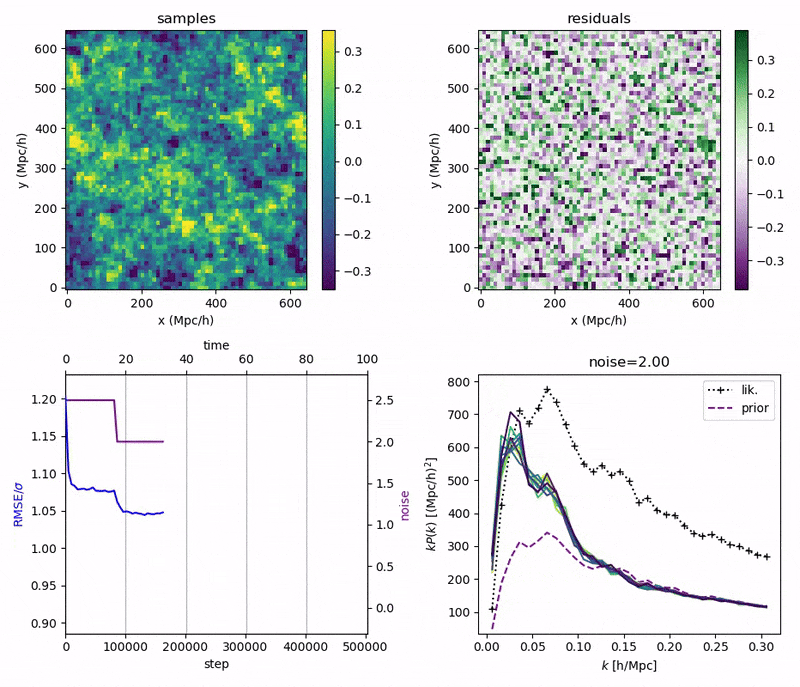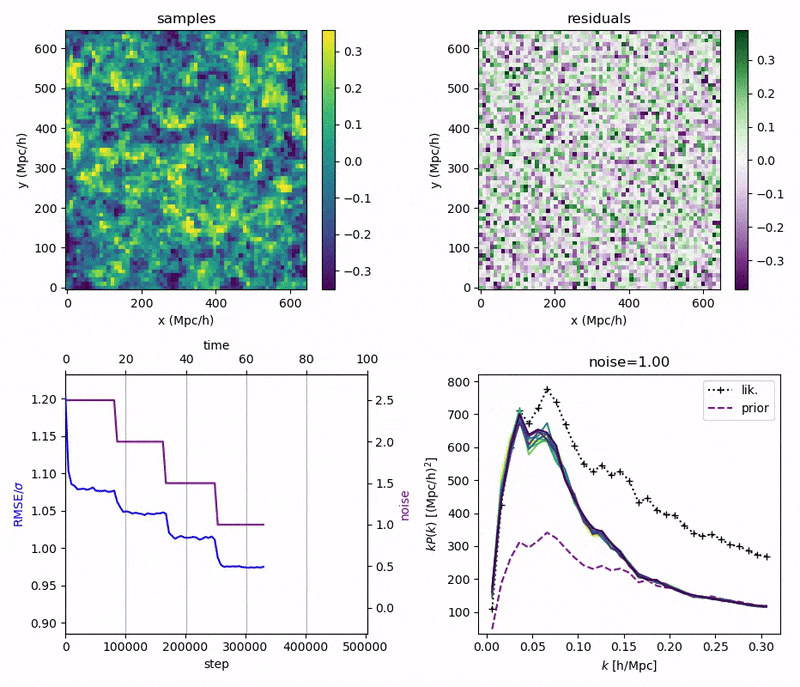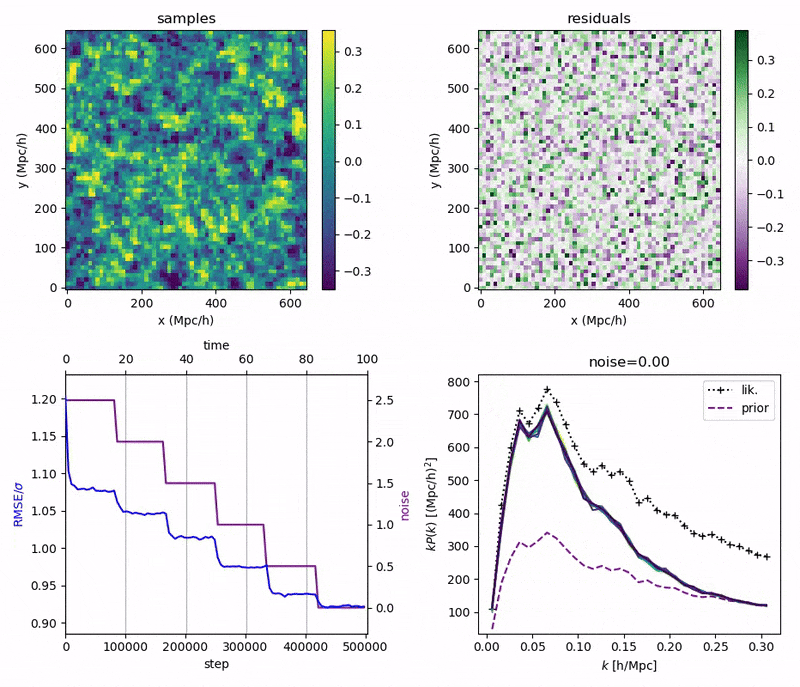
Idea: a custom annealed Langevin
- continuously anneal target distribution, e.g.
  $$p_{s}(z,x_0) := \mathcal N(x_0 \mid f(z), \Sigma + s^2 I) \, p(z)$$
- solve SDE $${\displaystyle {d {z}}=\nabla \log p_{s(t)} (z , x_0)dt+{\sqrt {2}}{d {W}}}$$
- optimize annealing policy $s(t)$?

Meanwhile, NUTS

Preliminary samples from model

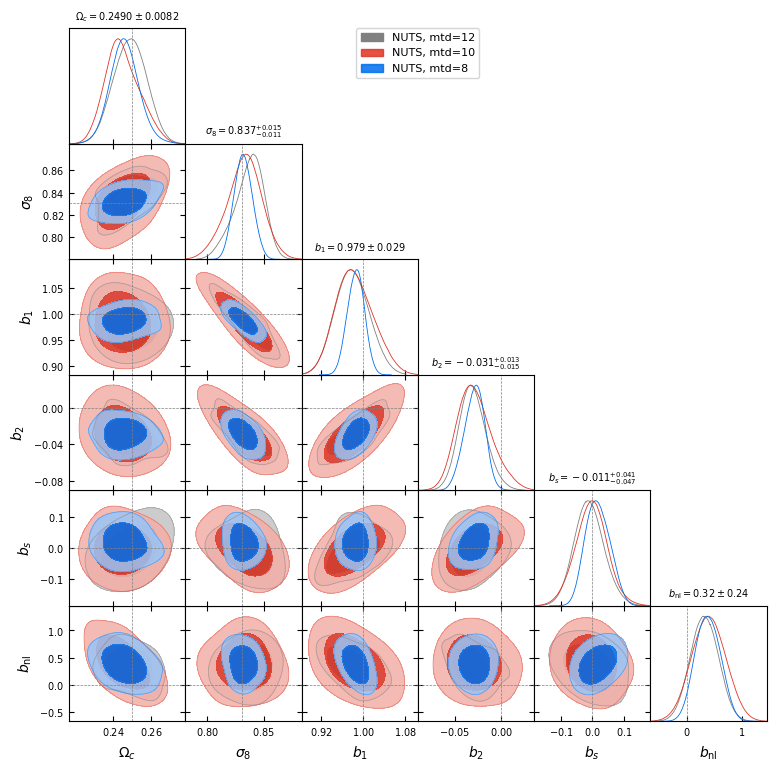
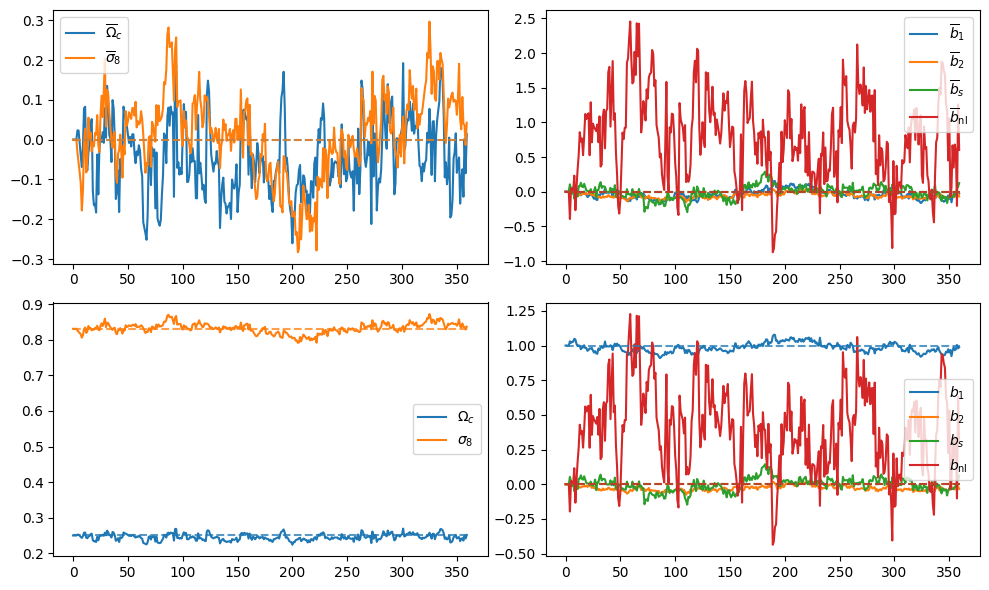
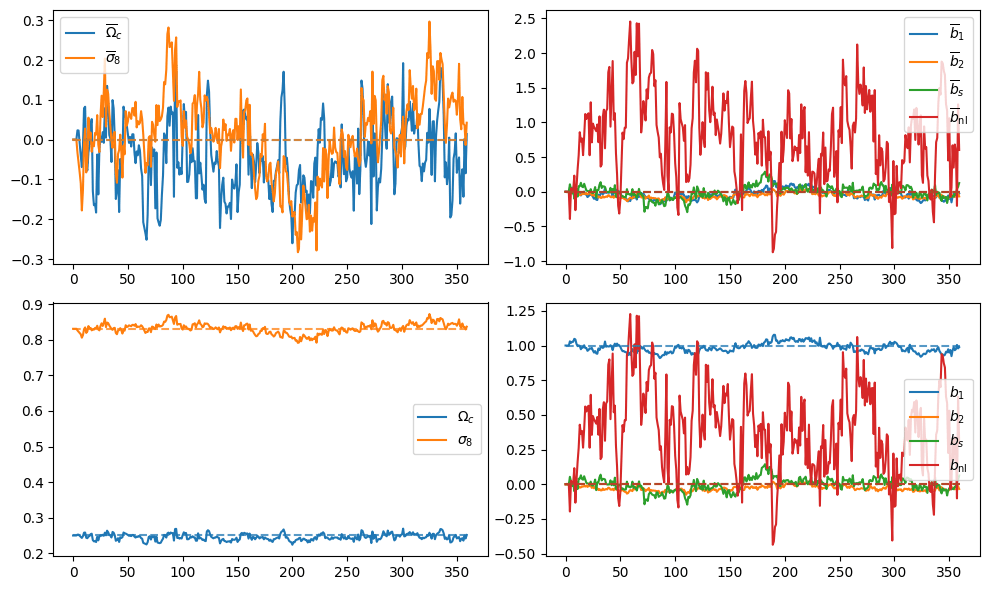
What about Implicit Likelihood Inference?

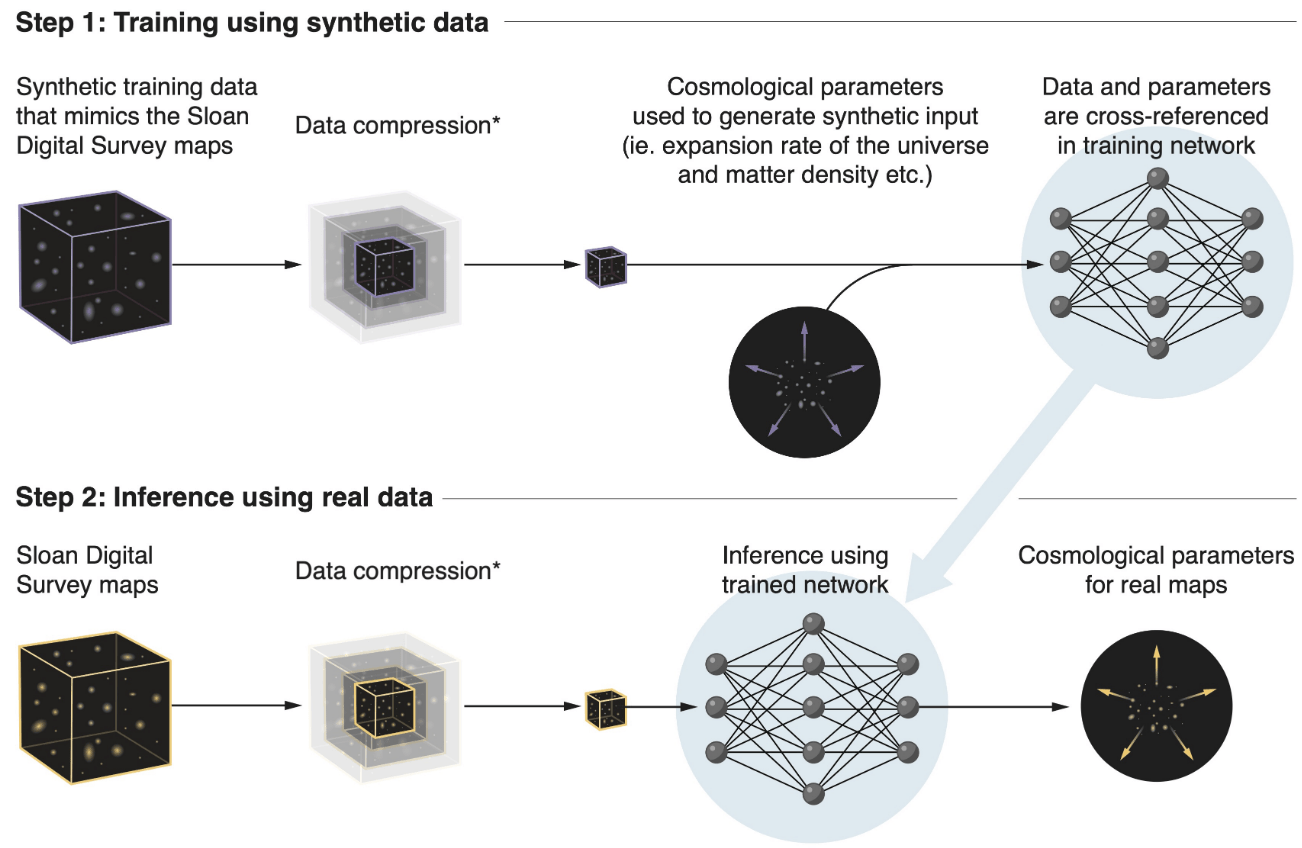
Aims

Cross-validate model
Studying Annealed Langevin
- optimal annealing policy?
- SDE solvers?
- translate SDE to PDE?
Benchmark samplers
- compare to SBI methods

2024z2C

By hsimonfroy

Field-level inference from galaxy surveys

Context

Modeling

Some useful programming tools

So JAX in practice?

So NumPyro in practice?

Now let's build a cosmological model!

What does it look like?

Sampling

Always Bayes

Random Walk Metropolis-Hasting

Let's use the score: Langevin dynamics

Not good enough? Let's heat things up

Not good enough? Let's heat things up

Use the score (again): Hamiltonian Monte Carlo

Model Inference

Benchmarking samplers

"Continuously Annealed Langevin Algorithm"

Meanwhile, NUTS

What about Implicit Likelihood Inference?

Aims

2024z2C

More from hsimonfroy