19AIE205
Sleep stage classification using different ML algorithms
Python for Machine Learning
Aadharsh Aadhithya - CB.EN.U4AIE20001
Anirudh Edpuganti - CB.EN.U4AIE20005
Madhav Kishore - CB.EN.U4AIE20033
Onteddu Chaitanya Reddy - CB.EN.U4AIE20045
Pillalamarri Akshaya - CB.EN.U4AIE20049
Team-1
Sleep stage classification using different ML algorithms
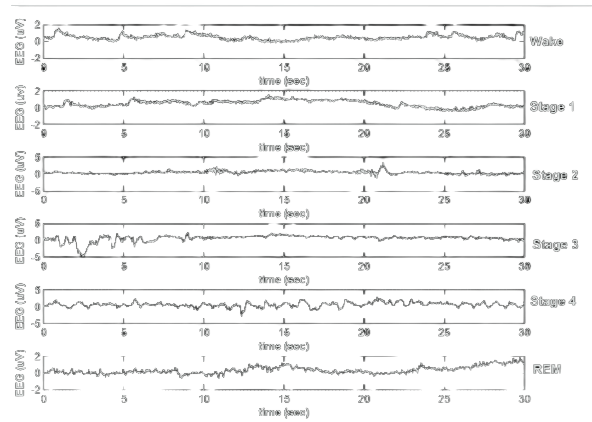
DataSet
DataSet
Delta
Theta
Alpha
Beta
K-Complex
0.5-4
4-8
8-13
13-22
0.5-1.5
Hz
Hz
Hz
Hz
Hz
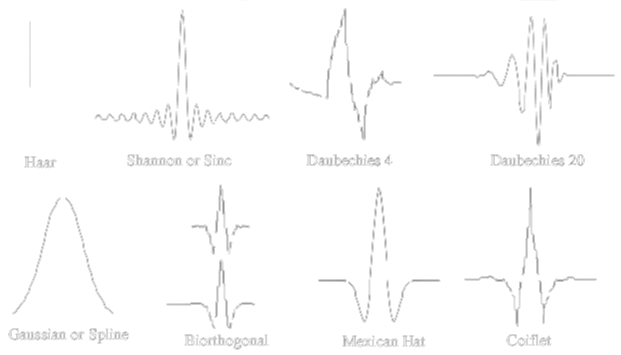
Continious Wavelet Transform
Time-Frequency Analysis Framework
Continious Wavelet Transform
Time-Frequency Analysis Framework
Wa,b=∫s(t)ψa,b(t)dt
W_{a,b} = \int s(t) \psi_{a,b}(t) dt
ψa,b(t)=a1ψ(at−b)
\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi(\frac{t-b}{a})
Continious Wavelet Transform
Time-Frequency Analysis Framework
Wa,b=∫s(t)ψa,b(t)dt
W_{a,b} = \int s(t) \psi_{a,b}(t) dt
ψa,b(t)=a1ψ(at−b)
\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi(\frac{t-b}{a})
Similarity
Measure
Mother
Wavelet
Continious Wavelet Transform
Time-Frequency Analysis Framework
Wa,b=∫s(t)ψa,b(t)dt
W_{a,b} = \int s(t) \psi_{a,b}(t) dt
ψa,b(t)=a1ψ(at−b)
\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi(\frac{t-b}{a})
Continious Wavelet Transform
Time-Frequency Analysis Framework
Wa,b=∫s(t)ψa,b(t)dt
W_{a,b} = \int s(t) \psi_{a,b}(t) dt
ψa,b(t)=a1ψ(at−b)
\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi(\frac{t-b}{a})
a→Streching or Shrinking
a \rightarrow \text{Streching or Shrinking}
b→translation along time
b \rightarrow \text{translation along time}
Continious Wavelet Transform
Time-Frequency Analysis Framework
Wa,b=∫s(t)ψa,b(t)dt
W_{a,b} = \int s(t) \psi_{a,b}(t) dt
ψa,b(t)=a1ψ(at−b)
\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi(\frac{t-b}{a})
f=aTsfc
f = \frac{f_c}{a T_s}
Delta
Theta
Alpha
Beta1
K-Complex
0.5-4
4-8
8-13
13-22
0.5-1.5
Hz
Hz
Hz
Hz
Hz
Beta2
22-35
Hz
Sleep spindles
12-14
Hz
s(t)
s(t)
CWT
∫s(t)ψa,b(t)dt
\int s(t) \psi_{a,b}(t) dt
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
Delta
Theta
Alpha
Beta1
K-Complex
0.5-4
4-8
8-13
13-22
0.5-1.5
Hz
Hz
Hz
Hz
Hz
Beta2
22-35
Hz
Sleep spindles
12-14
Hz
s(t)
s(t)
CWT
∫s(t)ψa,b(t)dt
\int s(t) \psi_{a,b}(t) dt
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
E=−∑pilog(pi)
E = - \sum p_i log(p_i)
Features
Random Forest
Random Forest
Dataset
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Random Forest
Dataset
| idx | x1 | x2 | x3 | y |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Data 1
Random Forest
Dataset
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Data 1
Random Forest
Dataset
| 3 | 1.1 | 3.1 | 2.8 | 3 |
|---|
| idx | x1 | x2 | x3 | y |
|---|
| . | . | . | . | . |
|---|
| . | . | . | . | . |
|---|
| 1 | 1.2 | 3.4 | 4.5 | 0 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
| 2 | 1.5 | 2.3 | 4.1 | 1 |
|---|
Data 1
Random Feature Selection
Random Forest
Dataset
Data 1
Random Forest
Dataset
Data 1
Data 2
Random Forest
Dataset
Data 1
Data 2
Data 3
Random Forest
Dataset
Data 1
Data 2
Data 3
Data 4
Random Forest
Dataset
Data 1
Data 2
Data 3
Data 4
Data 5
Random Forest
Dataset
Data 1
Data 2
Data 3
Data 4
Data 5
Bootstrapped Data
Random Forest
Dataset
Data 1
Data 2
Data 3
Data 4
Data 5
x1,x2
x_1,x_2
x1,x3
x_1,x_3
x1,x2
x_1,x_2
x2,x3
x_2,x_3
x1,x3
x_1,x_3
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Decision Tree
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
| x1 | x2 | x3 |
|---|
| x1 | x2 |
|---|---|
| 1.3 | 3.8 |
| 1.3 | 3.8 | 4.9 |
|---|
Predict
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
| x1 | x2 | x3 |
|---|
| 1.3 | 3.8 | 4.9 |
|---|
Predict
| x1 | x2 |
|---|---|
| 1.3 | 3.8 |
Prediction
0
Random Forest
Dataset
| x1 | x2 | x3 |
|---|
| 1.3 | 3.8 | 4.9 |
|---|
Predict
Prediction
0
Data 2
x1,x3
x_1,x_3
| x1 | x3 |
|---|---|
| 1.3 | 4.9 |
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
0
0
3
1
0
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
0
0
3
1
0
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
0
0
3
1
0
Majority Voting
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
0
0
3
1
0
Majority Voting
0
Random Forest
Dataset
Data 1
x1,x2
x_1,x_2
Data 2
Data 3
x1,x2
x_1,x_2
Data 4
x2,x3
x_2,x_3
Data 5
x1,x3
x_1,x_3
x1,x3
x_1,x_3
0
0
3
1
0
| x1 | x2 | x3 |
|---|
| 1.3 | 3.8 | 4.9 |
|---|
Labelled as
| y |
|---|
| 0 |
|---|
Support Vector Machine
Support Vector Machine
Text
Binary Classification
Support Vector Machine
Text
Binary Classification
Yes
No
Support Vector Machine
Text
Multi-Class Classification
Support Vector Machine
Text
Multi-Class Classification
Class 1
Class 2
Class 3
Support Vector Machine
Text
Multi-Class Classification
Class 1
Class 2
Class 3
Types
Support Vector Machine
Text
Multi-Class Classification
One vs Rest
One vs One
Support Vector Machine
Text
Multi-Class Classification
One vs Rest
One vs One
One vs One
Support Vector Machine
Text
Multi-Class Classification
One vs One
Labels
1
1
2
2
3
3
Support Vector Machine
Text
Multi-Class Classification
One vs One
1,2
1,2
2,3
2,3
1,3
1,3
Support Vector Machine
Text
Multi-Class Classification
One vs One
1,2
1,2
2,3
2,3
1,3
1,3
One vs Rest
Support Vector Machine
Text
Multi-Class Classification
1 vs 2,3
1\text{ vs } 2,3
One vs Rest
2 vs 1,3
2\text{ vs } 1,3
3 vs 1,2
3\text{ vs } 1,2
Support Vector Machine
Text
Multi-Class Classification
1 vs 2,3
1\text{ vs } 2,3
One vs Rest
2 vs 1,3
2\text{ vs } 1,3
3 vs 1,2
3\text{ vs } 1,2
INTUITION
Support Vector Machine
Text
One vs Rest
INTUITION
x1
x_1
x2
x_2
1
2
3
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
New data
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Ask
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Ask
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Ask
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
Ask
Text
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
x1
x_1
x2
x_2
K-Nearest Neighbours
K-Nearest Neighbours
x1
x_1
x2
x_2
K-Nearest Neighbours
New data
x1
x_1
x2
x_2
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=1
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=1
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=1
x1
x_1
x2
x_2
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=2
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=2
x1
x_1
x2
x_2
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=4
K-Nearest Neighbours
x1
x_1
x2
x_2
New data
Suppose K=4
x1
x_1
x2
x_2
Multi Layer Network
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
g(z1)1
g(z_{1})^1
g(z2)1
g(z_{2})^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
g(z1)2
g(z_{1})^2
y^
\hat{y}
Wi=w11iw21i⋮wm1iw12iw22i⋱wm2iw13iw23i⋱wm3i⋯⋯⋮⋯w1niw2niwmni
W^i = \begin{bmatrix}
w^i_{11} & w^i_{12} & w^i_{13} & \cdots&w^i_{1n} \\
w^i_{21} & w^i_{22} & w^i_{23} & \cdots&w^i_{2n} \\
\vdots & \ddots& \ddots & \vdots \\
w^i_{m1} & w^i_{m2} & w^i_{m3} & \cdots&w^i_{mn} \\
\end{bmatrix}
m→no .of neurons in ith layern→no .of neurons in (i−1)th layer
m \rightarrow \text{no .of neurons in } i^{th} \text{ layer} \\
n \rightarrow \text{no .of neurons in } (i-1)^{th} \text{ layer}
Xi=x1x2⋮xn
X^i = \begin{bmatrix}
x_1 \\
x_2\\
\vdots \\
x_n
\end{bmatrix}
Xi→Output of (i−1)th layern→no .of neurons in (i−1)th layer
X^i \rightarrow \text{Output of } (i-1)^{th} \text{ layer} \\
n \rightarrow \text{no .of neurons in } (i-1)^{th} \text{ layer}
bi=b1ib2i⋮bmi
b^i = \begin{bmatrix} b_1^i \\ b_2^i \\ \vdots \\ b_m^i \end{bmatrix}
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
g(z1)2
g(z_{1})^2
y^
\hat{y}
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
L(y,y^)
L(y,\hat{y})
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
g(z1)2
g(z_{1})^2
y^
\hat{y}
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
L(y,y^)
L(y,\hat{y})
Forward Pass
zi=Wi⋅xi+biyi=g(zi)
z^i = W^i \cdot x^i + b^i \\
y^i = g(z^i)
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
g(z1)2
g(z_{1})^2
y^
\hat{y}
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
L(y,y^)
L(y,\hat{y})
Forward Pass
z1=W1⋅x1+b1
z^1 = W^1 \cdot x^1 + b^1 \\
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
g(z1)2
g(z_{1})^2
y^
\hat{y}
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
L(y,y^)
L(y,\hat{y})
Forward Pass
y1=g(z1)
y^1 = g(z^1)
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
Forward Pass
⋯yi=g(zi)
\cdots \\
y^i = g(z^i)
g(z1)1
g(z_{1})^1
g(z2)1
g(z_{2})^1
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
Forward Pass
⋯yi=g(zi)
\cdots \\
y^i = g(z^i)
g(z1)1
g(z_{1})^1
g(z2)1
g(z_{2})^1
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Multi Layer Network
x1
x_1
w111
w_{11}^1
x3
x_3
x2
x_2
w121
w_{12}^1
w131
w_{13}^1
w211
w_{21}^1
w221
w_{22}^1
w231
w_{23}^1
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
⋯yi=g(zi)
\cdots \\
y^i = g(z^i)
g(z1)1
g(z_{1})^1
g(z2)1
g(z_{2})^1
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
wjki→ithlayer ,jthneuron , mapping to kth input
w_{j k}^i \rightarrow i^{th} \text{layer ,} j^{th} \text{neuron , mapping to } k^{th} \text{ input}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
changing y^ changes L(y,y^)
\text{changing } \hat{y} \text{ changes } L(y,\hat{y})
∂y^∂L(y,y^)∂wjki∂y^
\frac{\partial L(y , \hat{y} )}{\partial \hat{y} } \frac{\partial \hat{y} }{\partial w^i_{jk}}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
changing y^ changes L(y,y^)
\text{changing } \hat{y} \text{ changes } L(y,\hat{y})
∂y^∂L(y,y^)∂wjki∂y^
\frac{\partial L(y , \hat{y} )}{\partial \hat{y} } \frac{\partial \hat{y} }{\partial w^i_{jk}}
We can derive
To Be Computed
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
changing y^ changes L(y,y^)
\text{changing } \hat{y} \text{ changes } L(y,\hat{y})
∂y^∂L(y,y^)∂wjki∂y^
\frac{\partial L(y , \hat{y} )}{\partial \hat{y} } \frac{\partial \hat{y} }{\partial w^i_{jk}}
We can derive
To Be Computed
Here , We Can Resort To Using The Chain Rule .
How G changes with x?
Changing x changes h(x)
dxdh(x)
\frac{d h(x)}{dx}
Changing h changes g
dhdg
\frac{d g}{dh}
dxdg=dxdh(x)⋅dhdg
\frac{dg} {dx} = \frac{d h(x)}{dx} \cdot \frac{d g}{dh}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
w112
w_{11}^2
w122
w_{12}^2
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
How do we reach wjki FromL(y,y^)
\text{How do we reach } w^i_{jk} \text{ From} L(y,\hat{y})
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
How do we reach wjki From L(y,y^)??
\text{How do we reach } w^i_{jk} \text{ From } L(y,\hat{y}) ??
Follow The RED Path !
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How L(y,y^) changes with y^
\text{How } L(y , \hat{y} ) \text{ changes with } \hat{y}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)2
\Sigma\\
(z_1)^2
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1
\Sigma\\
z_1
Σz2
\Sigma \\ z_2
g(z2)
g(z_2)
g(z‘)
g(z_`)
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How y^ changes with (z1)i+1
\text{How } \hat{y} \text{ changes with } (z_1)^{i+1}
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)i+1
\Sigma\\
(z_1)^{i+1}
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1i
\Sigma\\
z_1^i
Σz2i
\Sigma \\ z_2^i
g(z2)i
g(z_2)^i
g(z1)i
g(z_1)^i
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How z1i+1 changes with g(zii)
\text{How } z_1^{i+1} \text{ changes with } g(z_i^i)
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)i+1
\Sigma\\
(z_1)^{i+1}
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1i
\Sigma\\
z_1^i
Σz2i
\Sigma \\ z_2^i
g(z2)i
g(z_2)^i
g(z1)i
g(z_1)^i
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How g(z1)i changes with z1i
\text{How } g(z_1)^i \text{ changes with } z_1^i
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
∂z1i∂g(z1)i
\frac{\partial g(z_1)^i }{\partial z_1^i}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)i+1
\Sigma\\
(z_1)^{i+1}
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1i
\Sigma\\
z_1^i
Σz2i
\Sigma \\ z_2^i
g(z2)i
g(z_2)^i
g(z1)i
g(z_1)^i
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How z1i changes with wjki
\text{How } z_1^i \text{ changes with } w^i_{jk}
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
∂z1i∂g(z1)i
\frac{\partial g(z_1)^i }{\partial z_1^i}
∂wjki∂z1i
\frac{\partial z_1^i}{\partial w^i_{jk}}
Multi Layer Network
x1
x_1
x3
x_3
x2
x_2
wjki
w_{j k}^i
y^
\hat{y}
L(y,y^)
L(y,\hat{y})
BackPropagation
Σ
\Sigma
∫
\int
Σ(z1)i+1
\Sigma\\
(z_1)^{i+1}
(g(z1))2
(g(z_1))^2
Σ
\Sigma
∫
\int
Σz1i
\Sigma\\
z_1^i
Σz2i
\Sigma \\ z_2^i
g(z2)i
g(z_2)^i
g(z1)i
g(z_1)^i
w111
w_{11}^1
w121
w_{12}^1
w221
w_{22}^1
w231
w_{23}^1
⋯
\cdots
∂wjki∂L(y,y^)=
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}} =
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
How L(y,y^) changes with wjki
\text{How } L(y,\hat{y} ) \text{ changes with } w^i_{jk}
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
∂z1i∂g(z1)i
\frac{\partial g(z_1)^i }{\partial z_1^i}
∂wjki∂z1i
\frac{\partial z_1^i}{\partial w^i_{jk}}
∂wjki∂z1i
\frac{\partial z_1^i}{\partial w^i_{jk}}
∂z1i∂g(z1)i
\frac{\partial g(z_1)^i }{\partial z_1^i}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
Multi Layer Network
BackPropagation
∂wjki∂L(y,y^)=
\frac{\partial L(y , \hat{y} )}{\partial w^i_{jk}} =
∂wjki∂z1i
\frac{\partial z_1^i}{\partial w^i_{jk}}
∂z1i∂g(z1)i
\frac{\partial g(z_1)^i }{\partial z_1^i}
∂g(zii)∂z1i+1
\frac{\partial z_1^{i+1} }{\partial g(z_i^i)}
∂(z1)i+1∂y^
\frac{\partial \hat{y}}{\partial (z_1)^{i+1}}
∂y^∂L(y,y^)
\frac{\partial L(y,\hat{y})}{\partial \hat{y}}
This is for one weights wjkifor the matrix Wi We Have a Detailed Derivation in the accompanying material
\text{ This is for one weights } w_{jk}^i \\ \text{for the matrix } W^i \text{ We Have a Detailed Derivation in the accompanying material}
For Softmax output layer and Sigmoid Activation function
Multi Layer Network
BackPropagation
Multi Layer Network
BackPropagation
Multi Layer Network
BackPropagation
Multi Layer Network
BackPropagation
So , now , we have all the vectorized components to build our chain
Multi Layer Network
Full Story
Thank you Mam!
19AIE205 Sleep stage classification using different ML algorithms Python for Machine Learning
PML Proj S3
By Incredeble us
PML Proj S3
- 82
