Reinforcement Learning (to-update-version)

Agenda

Caso de estudio
Proceso de decisión Markoviana
Aprendizaje reforzado
- Q-learning
- Deep Q-learning
Ejemplo: MountainCar

Ágora

Caso de estudio: Navegación terrestre

¿Cómo bajar esta montaña de la mejor manera?

Aprendizaje supervisado

Aprendizaje reforzado

Caso de estudio: Navegación lunar

¿Cómo explorar ~~cualquier planeta~~ la luna ?

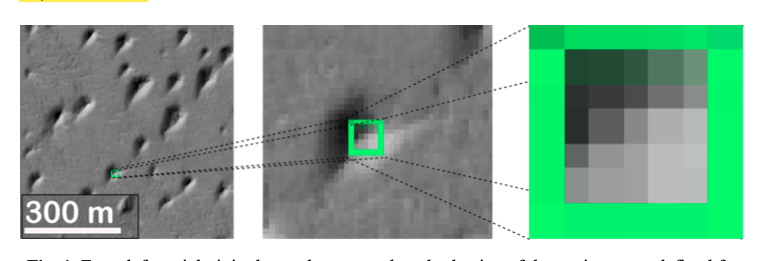
Caso de estudio: Navegación lunar

¿Cómo explorar ~~cualquier planeta~~ la luna ?

Mapa

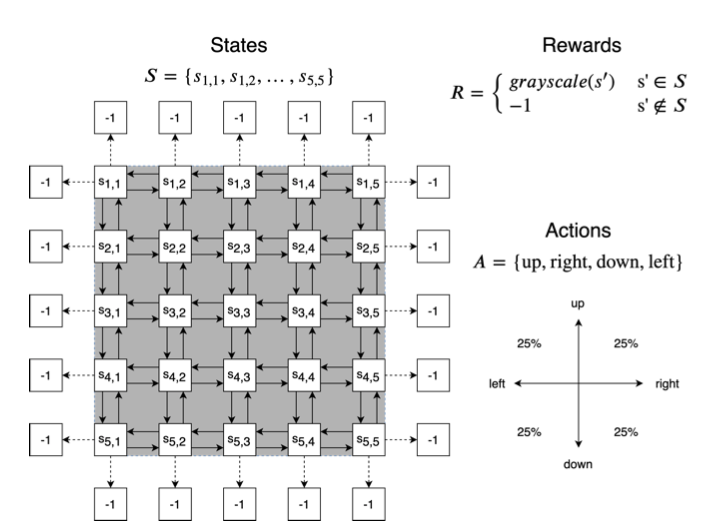
Caso de estudio: Navegación lunar

¿Cómo encontrar ese mapa?

Aprendizaje supervisado

El "maestro" indica al agente la respuesta esperada
El agente crea un modelo basado en sus respuestas y las esperadas $f(y,\hat{y})$

Aprendizaje sensitivo-al-costo

El entorno proveé una señal de recompensa $r(s,a)$
Aplicación:
- Optimización de comportamiento

Aprendizaje reforzado

El entorno proveé el valor de su estado, dada su acción $q_{\pi}(s,a)$
¿Qué tan bueno es -10.45?
- Necesidad de exploración

$s_{0,0}$

$s_{1,0}$

$s_{2,0}$

$s_{3,0}$

$s_{4,0}$

$s_{0,1}$

$s_{1,1}$

$s_{2,1}$

$s_{3,1}$

$s_{4,1}$

$s_{0,2}$

$s_{1,2}$

$s_{2,2}$

$s_{3,2}$

$s_{4,2}$

$s_{0,3}$

$s_{1,3}$

$s_{2,3}$

$s_{3,3}$

$s_{4,3}$

$s_{0,4}$

$s_{1,4}$

$s_{2,4}$

$s_{3,4}$

$s_{4,4}$

Espacio de estados

Entorno

↓

↑

→

←

→

$r=-100$

$r=-1000$

$r=1$

$r=1000$

$r=-1$

Recompensas

Acciones

$a_0$

$a_1$

$a_2$

$a_3$

$s_{0,0}$

$s_{1,0}$

$s_{2,0}$

$s_{3,0}$

$s_{4,0}$

$s_{0,1}$

$s_{1,1}$

$s_{2,1}$

$s_{3,1}$

$s_{4,1}$

$s_{0,2}$

$s_{1,2}$

$s_{2,2}$

$s_{3,2}$

$s_{4,2}$

$s_{0,3}$

$s_{1,3}$

$s_{2,3}$

$s_{3,3}$

$s_{4,3}$

$s_{0,4}$

$s_{1,4}$

$s_{2,4}$

$s_{3,4}$

$s_{4,4}$

↑

$a_0$

→

$a_1$

→

$a_1$

↓

$a_2$

↓

$a_2$

←

$a_3$

↓

$a_2$

→

$a_1$

¿Cuánto vale la trayectoria ${V^*(s)}$ óptima)?

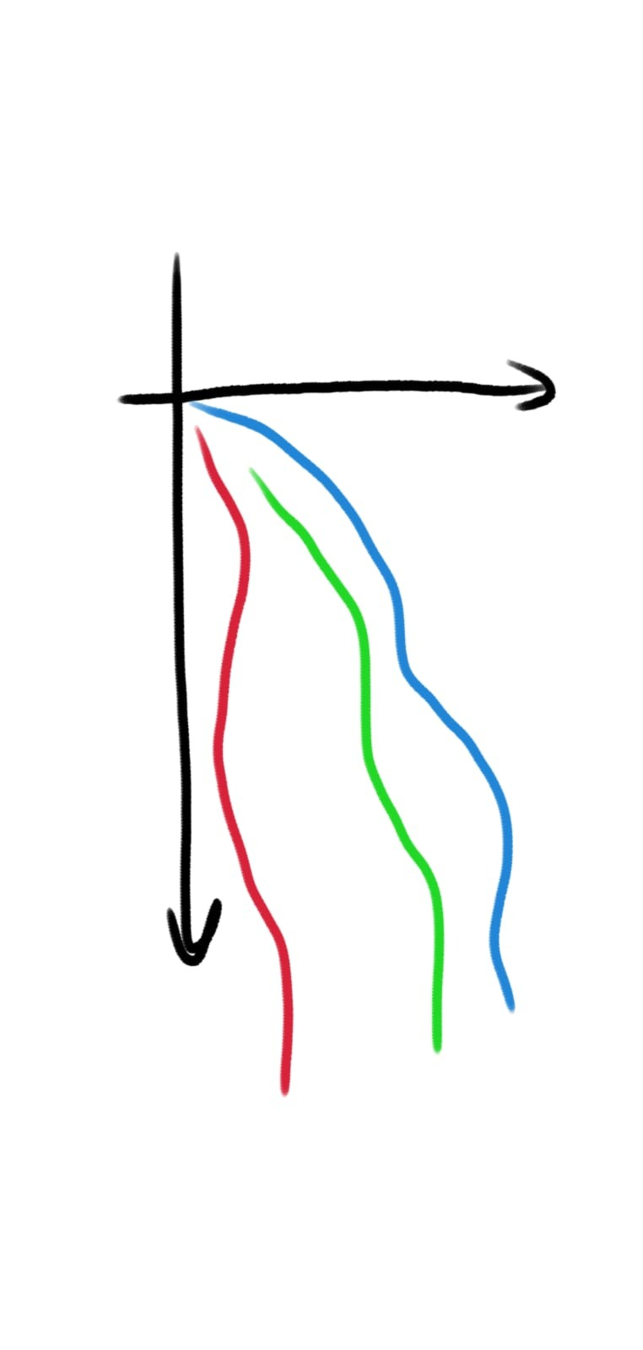
${V^*(s)}$

Value function

$S$

$s_{0,1}$

$s_{0,2}$

$s_{1,2}$

$s_{2,2}$

$s_{3,2}$

$s_{0,3}$

$s_{1,3}$

$s_{3,3}$

$s_{1,1}$

↑

→

↓

←

↓

→

$a_1$

$a_2$

$a_3$

$a_2$

$a_1$

$a_0$

$s_{0,0}$

$s_{1,0}$

$s_{2,0}$

$s_{3,0}$

$s_{4,0}$

$s_{0,1}$

$s_{1,1}$

$s_{2,1}$

$s_{3,1}$

$s_{4,1}$

$s_{0,2}$

$s_{1,2}$

$s_{2,2}$

$s_{3,2}$

$s_{4,2}$

$s_{0,3}$

$s_{1,3}$

$s_{2,3}$

$s_{3,3}$

$s_{4,3}$

$s_{0,4}$

$s_{1,4}$

$s_{2,4}$

$s_{3,4}$

$s_{4,4}$

↑

$a_0$

→

$a_1$

→

$a_1$

↓

$a_2$

↓

$a_2$

←

$a_3$

↓

$a_2$

→

$a_1$

¿Cuáles son los mejores estados?

¿Cuáles son las mejores acciones?

MDP genera un problema secuencial

Action-Value function $Q_{\pi}:S \times A→\R$

$q(s,a):E[R_{t+1}+{\gamma}{q(s_{t+1}, a_{t+1})} | S_t=s, A_t=a]$

Value function $V_{\pi}:S→\R$

$v(s):E[R_{t+1}+{\gamma}{v(s_{t+1})} | S_t=s]$

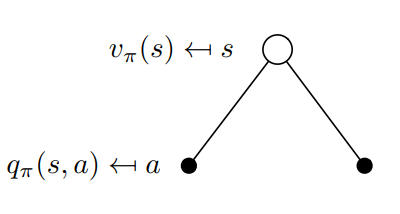
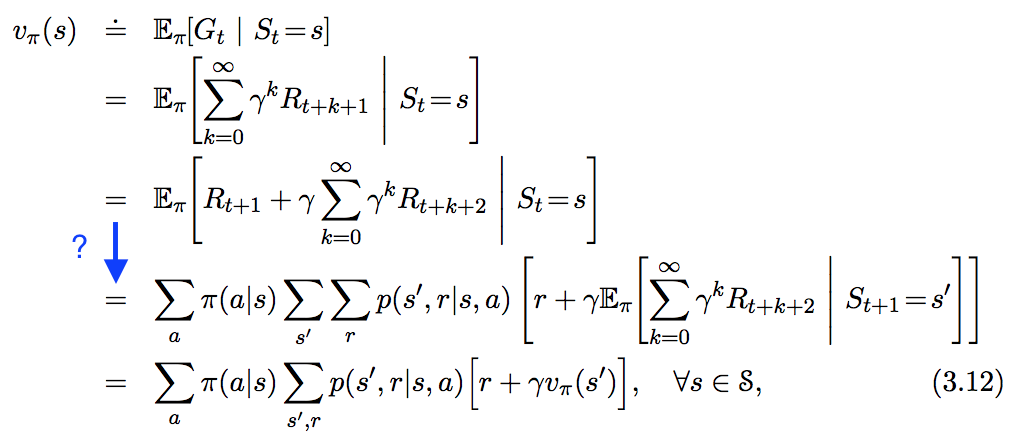
$v_{\pi}(s):\Bbb{E}_{\pi}[R_{t+1}+{\gamma}{v(s_{t+1})} | S_t=s]$

Función de valor $V_{\pi}:S→\R$

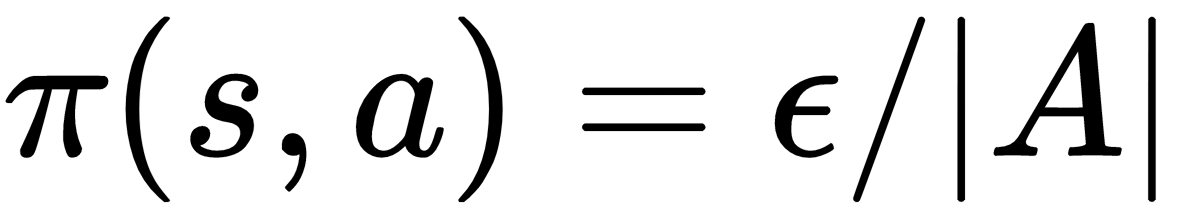
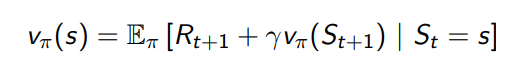
$v(s):E[R_{t+1}+{\gamma}{v(s_{t+1})} | S_t=s]$

Política: $\epsilon$-greedy

Ecuación de expectativas de Bellman

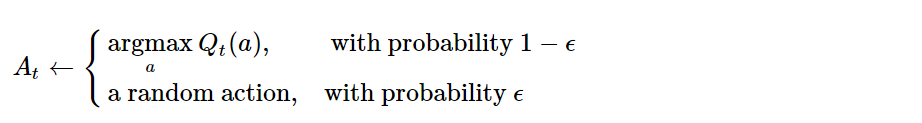
Función de acción-valor $Q_{\pi}:S \times A→\R$

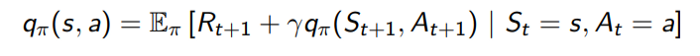
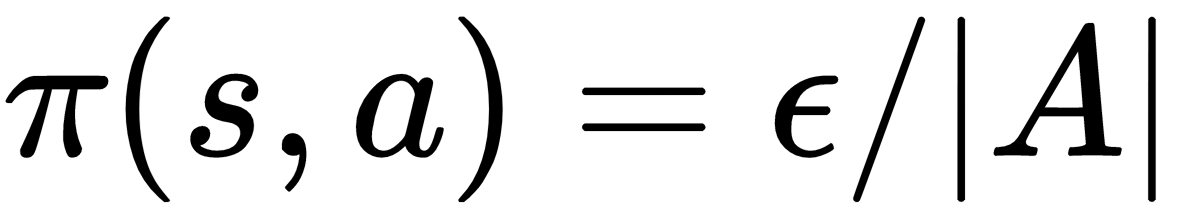
$q(s,a):E[R_{t+1}+{\gamma}{q(s_{t+1}, a_{t+1})} | S_t=s, A_t=a]$

Política: $\epsilon$-greedy

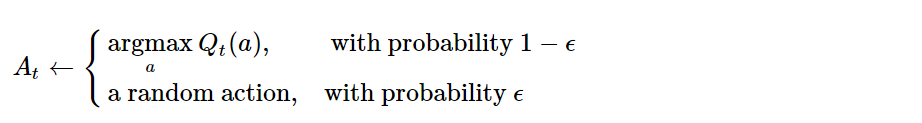
Ecuación de expectativas de Bellman

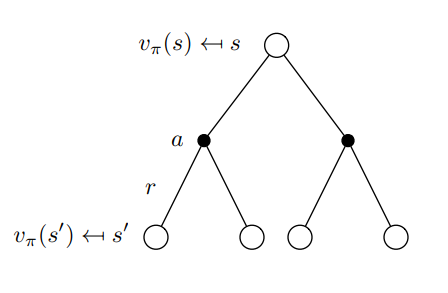
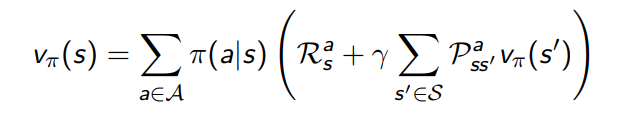
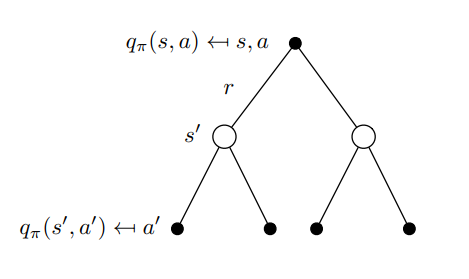
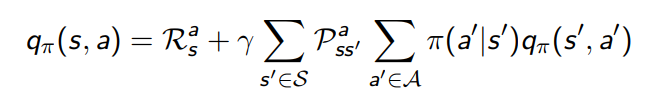
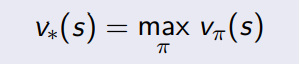
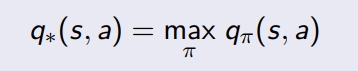
Cálculo del valor de los estados

Valor óptimo

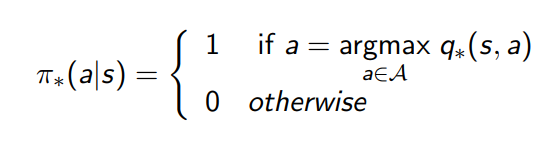
${\pi}^{'}$

${\pi}$

Value function

$S$

¿La política actual es mejor que la anterior?

¿Cuál es la política óptima?

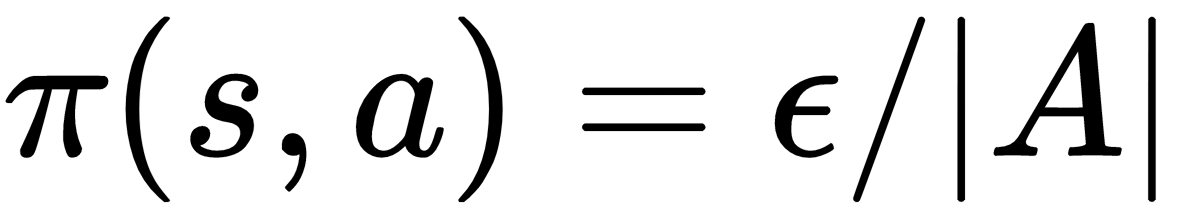
Política: $\epsilon$-greedy

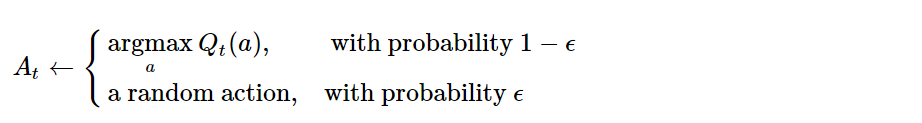
$S$

$b$

$k_0$

$k_1$

$k_2$

$k_5$

$k_{4}$

$k_{3}$

Nodo inicial artificial

Nodo final artificial

$x_0$

$x_1$

$x_2$

$x_3$

$x_4$

$x_5$

$x^3_0$

$x^2_0$

$x^1_0$

$x^0_0$

$x^3_1$

$x^2_1$

$x^1_1$

$x^0_1$

$x^0_2$

$x^1_2$

$x^2_2$

$x^3_2$

$x^2_3$

$a$

$x^4_3$

$x^3_2$

$x^4_2$

$x^1_3$

$x^0_3$

$x^3_4$

$x^2_4$

$x^1_4$

$x^0_4$

$x^0_5$

$x^1_5$

$x^2_5$

$x^3_5$

Sistema dinámico discreto de horizonte finito

$k_0$

$k_1$

$k_2$

$k_5$

$k_{4}$

$k_{3}$

Sistema dinámico discreto de horizonte finito

0

Advanced issue found

▲

$x_0$

$x_1$

$x_2$

$x_3$

$x_4$

$x_5$

$u_0$

$u_1$

$u_3$

$u_4$

$u_5$

Donde: $x_i$ estados, $u_i$ controles (acciones), $k_i$ tiempo

Espacio de estados $S = x_0 \times x_1 \times x_1 \times x_3 \times x_4 \times x_5$

Ejemplo: $S = 10 \times 10 \times 10 \times 10 \times 10 \times 10 = 10^6 = 1,000,000$

$k_0$

$k_1$

$k_2$

$k_5$

$k_{4}$

$k_{3}$

$x_0$

$x_1$

$x_2$

$x_3$

$x_4$

$x_5$

$u_0$

$u_1$

$u_3$

$u_4$

$u_5$

Control óptimo de un sistema dinámico

$x_{k+1}$: sistema dinámico de tiempo discreto

$f_k$: función de actualización del sistema de tiempo $k$ al tiempo $k+1$

$g_{k}$: costo de transición al tiempo $k$

$N$: horizonte finito

$g_{N}$: costo de transición terminal

Formulación determinista de horizonte finito

Donde:

$x_k$

$x_{k+1}$

$x_N$

$x_0$

$x_{k+1}=f_k(x_k, u_k)$

Costo $g_k(x_k, u_k)$

Costo final

$g_N(x_N)$

Tiempo $k$

Futuro

Control $u_k$

Programación Dinámica (PD)

$S$

$b$

$a$

Secuencia de costos del control

$\{J(a+1),J(a+2),\dots,J(b-1)\}$

0

Advanced issue found

▲

$J(a+2)$

$J(a+1)$

$J(a+3)$

$J(b-1)$

$J(b-2)$

$J(b-3)$

$u_{b-1}$

$u_{b-2}$

$u_{b-3}$

$u_{b-4}$

$u_{a+2}$

$u_{a+1}$

$u_{a}$

$u_{a+3}$

Secuencia de control

$\{a:u_{a+1},\dots,u_{b-2}\}$

0

Advanced issue found

▲

Teorema: principio de optimalidad $^*$

(1)

Secuencia de estados óptimos

$\{x^*_0, \dots, x^*_{k}, \dots, x^*_{N}\}$ desde $x^*_0$

Subproblema $g(x^*_k,u^*_k)$

$x^*_{k}$

$k$

$x_N$

$N$

$u^*_k$

$\{u^*_0,\dots,$$u^*_k$$\}$

0

Advanced issue found

▲

$x^*_{0}$

$u^*_0$

Secuencia de control óptimo

$J^*(x^*_k)=g(x^*_k,u^*_k)+\sum_{m=k+1}^{N-1}g_m(x_m,u_m)+g_N(x_N)$

Costo final

$g_N(x_N)$

De manera general:

$0$

Secuencia de control óptimo

$\{u^*_0, \dots, u^*_{k}, \dots, u^*_{N-1}\}$ desde $x^*_0$

Secuencia de control

$\{u_0, \dots, u_{N-1}\}$

Secuencia de estados

$\{x_0, \dots, x_N\}$

(2)

(3)

Costo óptimo

Soluciones exactas vía PD (ecuaciones de Bellman)

$x_k$

$x_{k+1}$

$x_N$

$x_0$

$x_{k+1}=f_k(x_k, u_k)$

Costo $g_k(x_k, u_k)$

Tiempo $k$

Futuro

$$J(x_0;u_0,\dots,u_{N-1})=g_N(x_N)+\sum^{N-1}_{k=0}g_k(x_k,u_k)$$

$$J^*(x_0)=\min_{\substack{u_k \in U_k(x_k) \\ k=0,\dots,N-1}}J(x_0;u_0,\dots,u_{N-1})=\min_{u_k \in U_k(x_k)}[g_N(x_N)+\sum^{N-1}_{k=0}g_k(x_k,u_k)]$$

Costo final

$g_N(x_N)$

$u_{0}$

$u_{N-1}$

$u_{k}$

Soluciones exactas vía DP para problemas de control óptimo de horizonte finito

Secuencia de control óptimo o política $\pi^*$

Determinista	Estocástico

Exacto	Esperanza

$\{u_0,\dots,u_{N-1}\}$

$\{\mu_0,\dots,\mu_{N-1}\}$

Cálculo de la función de costo óptimo $J^*_k$ y la política óptima $\pi^*_k$

$$J^*_k=\min_{u_k \in U_k(x_k)}E[g_k(x_k,u_k,w_k)+J^*_{k+1}(x_k,u_k,w_k)]$$

$$\pi^*_k \in \arg \min_{u_k \in U_k(x_k)}E[g_k(x_k,u_k,w_k)+J^*_{k+1}(x_k,u_k,w_k)]$$

Secuencia de funciones de costo

$\{J^*_N(x_N), J^*_{N-1}(x_{N-1}) \dots, J^*_{0}(x_0)\}$

(5)

(4)

(2001) Teorema de Aproximación Universal

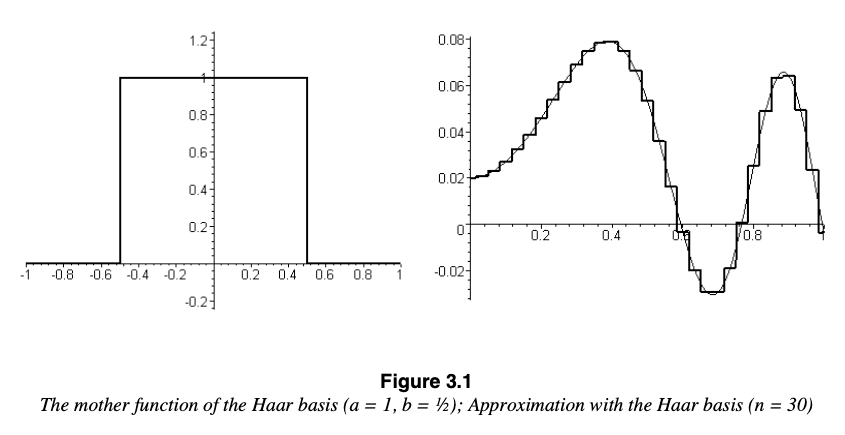
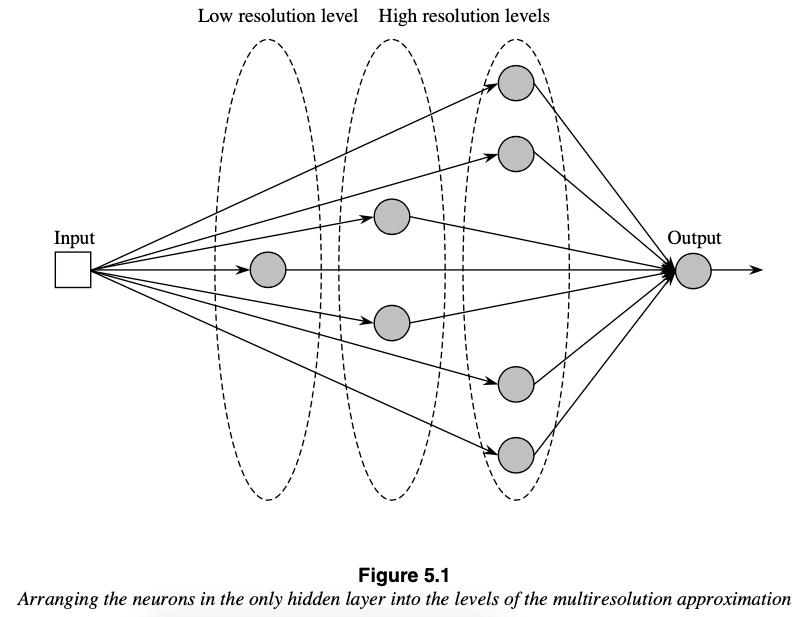
3) Aproximación con la función de activación Haar

($a=1, b=1/2, n=30$)

4) Aproximación multi-resolución (deep learning)

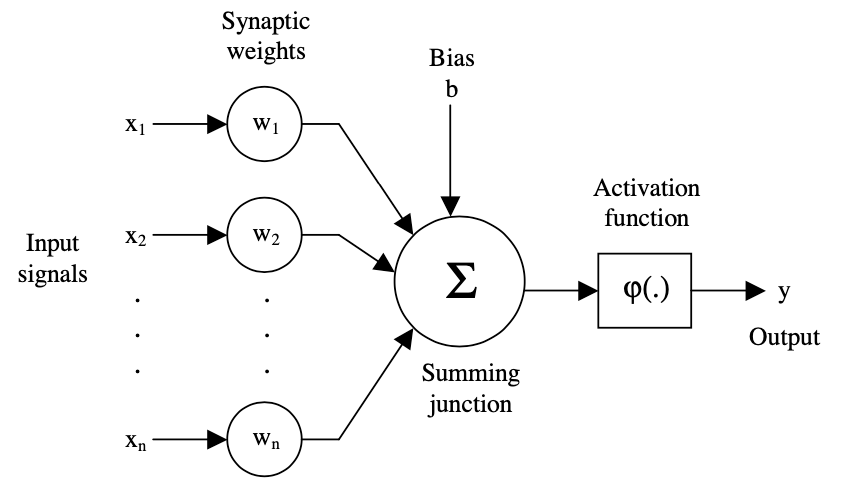
2) Modelo de una neurona no lineal

1) Teorema de aproximación universal

Aproximación en el espacio de estados

Donde

$x_{m,k}$: muestras del estado $x_k$

$r_k$: peso en $k$

$r'_k$: peso "afinado" en $k$

$\phi_k$: vector de características en la forma $\{\phi_{1,k}(x_k), \dots, \phi_{m,k}(x_k)\}$ asociados a $x_k$ en el tiempo $k$

$\hat{J}_k$: costo aproximado

Usar el costo aproximado $\hat{J}_{k}$ en lugar del costo óptimo $J^*_{k}$

Arquitectura de aproximación basada en características

$\hat{J}_{k}(\phi_{k}(x_{k}),r_k)$

0

Advanced issue found

▲

Vector de

características

$\phi_k(x_k)$

Extracción de características

Selección de

características

Estado

$x_k=x_{m,k}$

Costo aproximado

$r'_{k} \phi_k (x_k)$

(7)

Arquitectura de aproximación

1) Estructura del Perceptron, arquitectura de aproximación bioinspirada

Arquitecturas basadas en características lineales y no lineales

Imagen recuperada

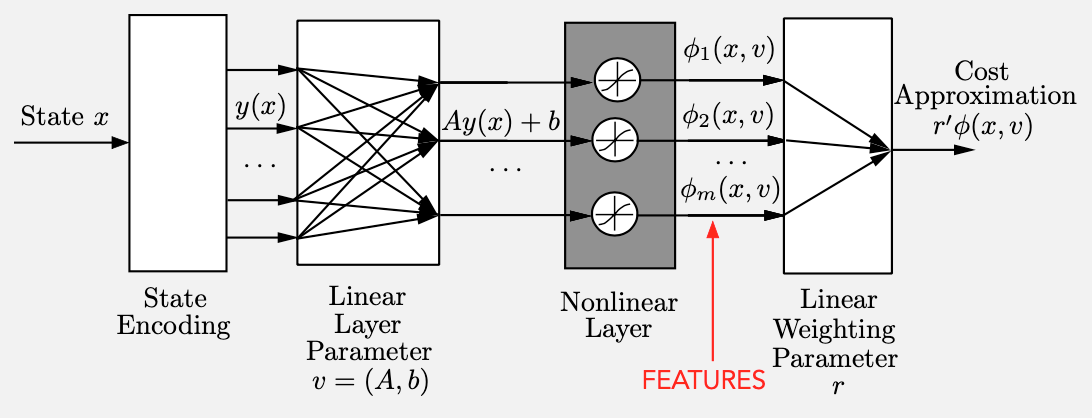
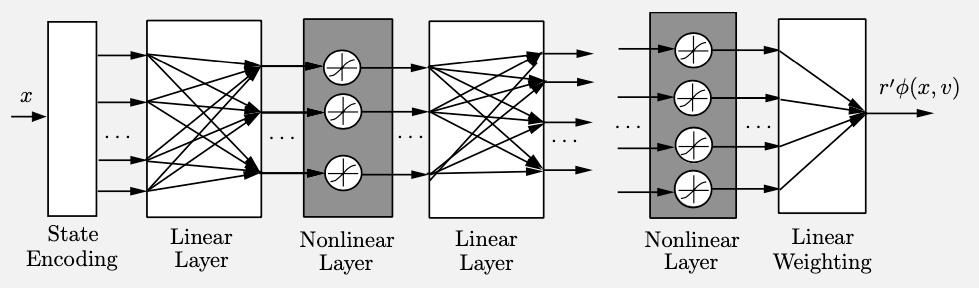
4) Red neuronal profunda con múltiples capas

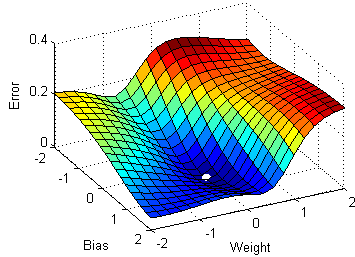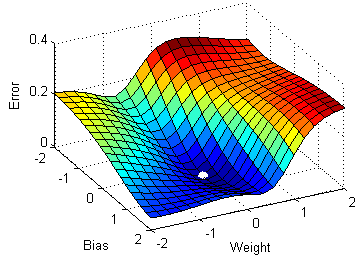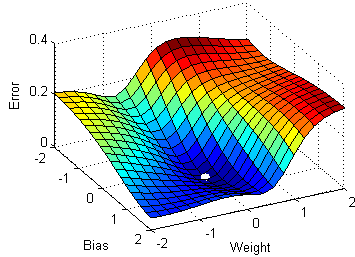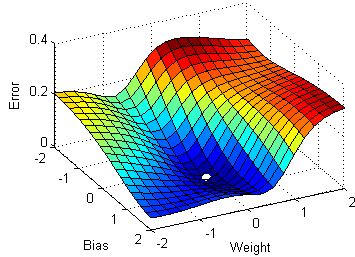
3) Función de costo

[2]

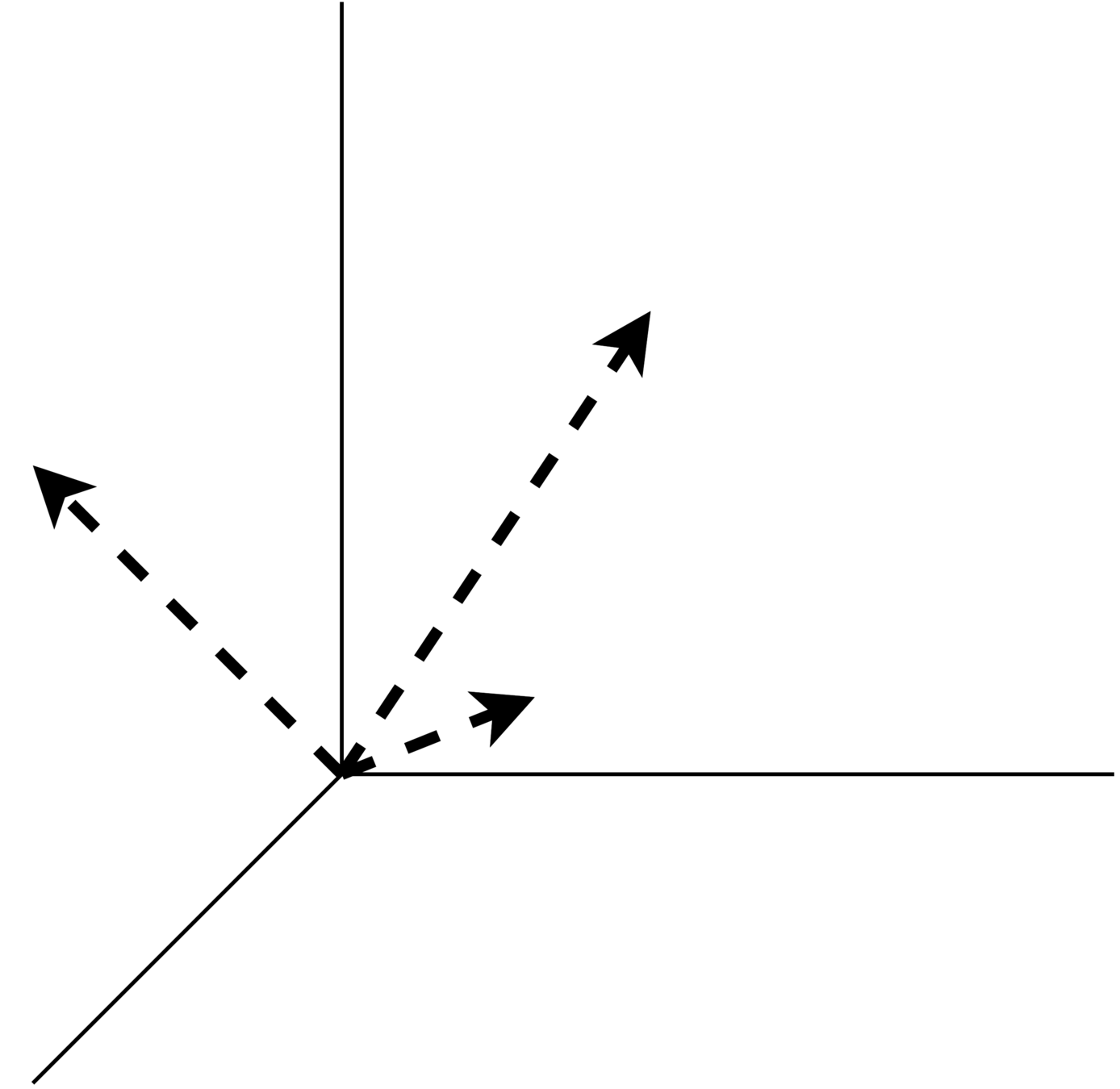
$x_1$

$x_2$

$x_3$

2) Modelo de espacio vectorial

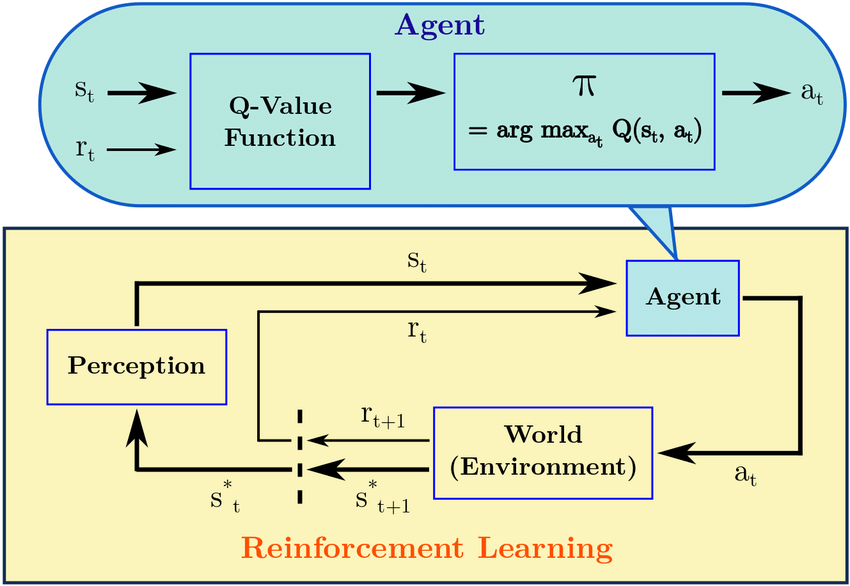
Aprendizaje reforzado

Algoritmo $Q-\text{learning}$

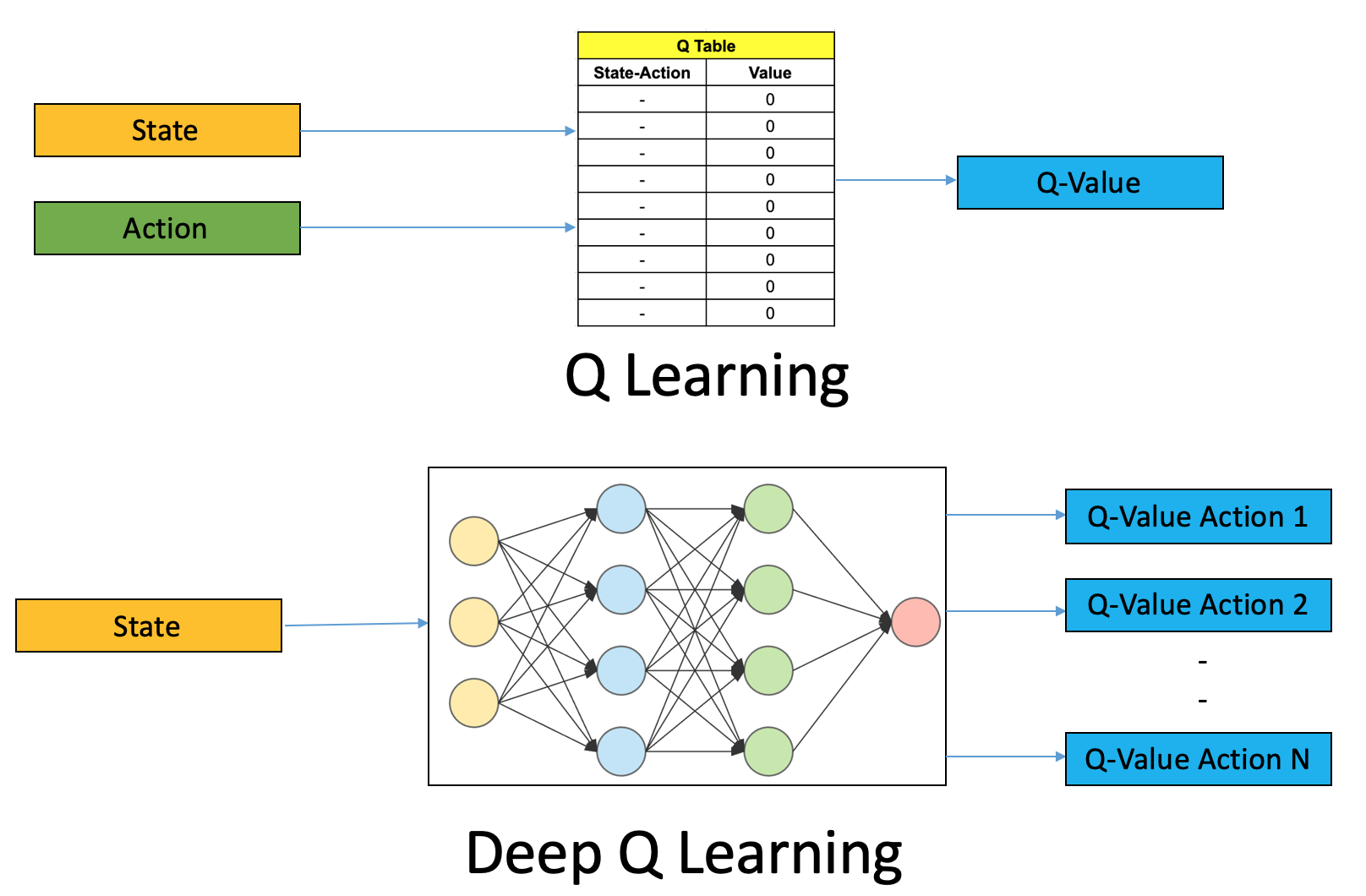
recompensa inmediata

factor de descuento

la mejor recompensa futura sobre todas las acciones

$Q(s,a) = \lbrace Q(s,a;\theta) - \lbrack r(s,a) + \gamma \max\limits_{a} Q(s,'a) \rbrack \rbrace ^{2} $

Aprendizaje reforzado

Algoritmo $DQN-\text{learning}$

$Q(s,a) = \lbrace Q(s,a;\theta) - \lbrack r(s,a) + \gamma \max\limits_{a} Q(s,'a) \rbrack \rbrace ^{2} $

$MSE=\frac{1}{n} \sum_{1}^{n} (y_i-\hat{y_i})^{2} $

función de aproximación $Q-\text{target}$

pesos (parámetros)

En un entorno desconocido

Un agente

Toma acciones basado en su propia política

Entonces su estado se actualiza

Y la evaluación de esa acción se da como una recompensa

Un laberinto

Un robot

Caminar

Moverse hacia delante

Puntuación

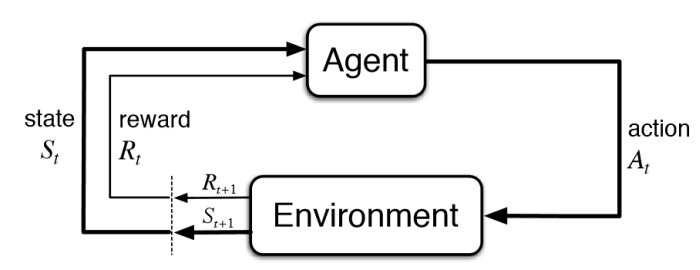
Markov Decission Process (MDP)

Entorno

Agente

Recompensa

Estado

Acción

Estados

2

3

4

5

6

7

8

9

10

11

13

14

15

16

17

12

Acciones

Transiciones

Recompensas

Recompensas inmediatas

Objetivo del AR

Que el agente encuentre su propia política para recibir la máxima cantidad de recompensas

Ganancia

Política

Trayectoria

Ejemplo

Problema: encontrar la trayectoria óptima que maximice la ganancia

Solución: dividir el problema en subproblemas (programación dinámica)

?

2

3

4

5

7

8

9

10

11

13

14

15

16

17

12

6

2 problemas

(encontrar el valor del estado 2 y 5)

4 sub-problemas

(encontrar el valor del estado 2, 5, 6 y 1)

Factor de descuento

2

3

4

5

7

8

9

10

11

13

15

16

17

12

6

10

11

14

15

$0.9^1$

$0.9^0$

$0.9^2$

$0.9^1$

$0.9$

$1$

$0.81$

$0.9$

$0.9^7$

$0.9^6$

$0.9^7$

$0.9^5$

$0.9^6$

$0.9^4$

$0.9^1$

$0.9^2$

$0.9^4$

$0.9^1$

$0.9^2$

$0.9^3$

$0.9^6$

$0.9^0$

$0.9^8$

$0.48$

$0.53$

$0.48$

$0.6$

$0.53$

$0.66$

$0.9$

$0.81$

$0.66$

$0.9$

$0.81$

$0.73$

$0.53$

Aprendizaje Reforzado:

Jacobo G. González León

Agenda

Ágora

Caso de estudio: Navegación terrestre

Caso de estudio: Navegación lunar

Caso de estudio: Navegación lunar

Caso de estudio: Navegación lunar

Aprendizaje supervisado

Aprendizaje sensitivo-al-costo

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Markov Decission Process (MDP)

Estados

Acciones

Transiciones

Recompensas

Recompensas inmediatas

Objetivo del AR

Ganancia

Política

Trayectoria

Ejemplo

Factor de descuento

Referencias

¡Muchas gracias!

@jacoboggleon

Reinforcement Learning (to-update-version)

Reinforcement Learning (to-update-version)

jacoboggleon

Aprendizaje Reforzado:

Jacobo G. González León

Agenda

Ágora

Caso de estudio: Navegación terrestre

Caso de estudio: Navegación lunar

Caso de estudio: Navegación lunar

Caso de estudio: Navegación lunar

Aprendizaje supervisado

Aprendizaje sensitivo-al-costo

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Aprendizaje reforzado

Markov Decission Process (MDP)

Estados

Acciones

Transiciones

Recompensas

Recompensas inmediatas

Objetivo del AR

Ganancia

Política

Trayectoria

Ejemplo

Factor de descuento

Referencias

¡Muchas gracias!

@jacoboggleon

Reinforcement Learning (to-update-version)

More from jacoboggleon