Aim 3: Posterior Sampling and Uncertainty
October 10, 2023
Measurement Model
y \sim \text{Poission}(N_0~e^{-Ax})
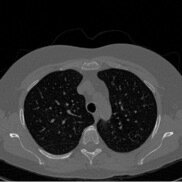
\(x\)
\(y\)
\(\text{FBP}(y)\)
Measurement Model
\(x\)
\(y\)
\(\text{FBP}(y)\)
Poisson model
Gaussian approximation
\[\lambda = N_0~e^{-Ax}\]
\[y \sim \text{Poisson}(\lambda)\]
\[y \sim \text{Normal}(\lambda, \lambda)\]
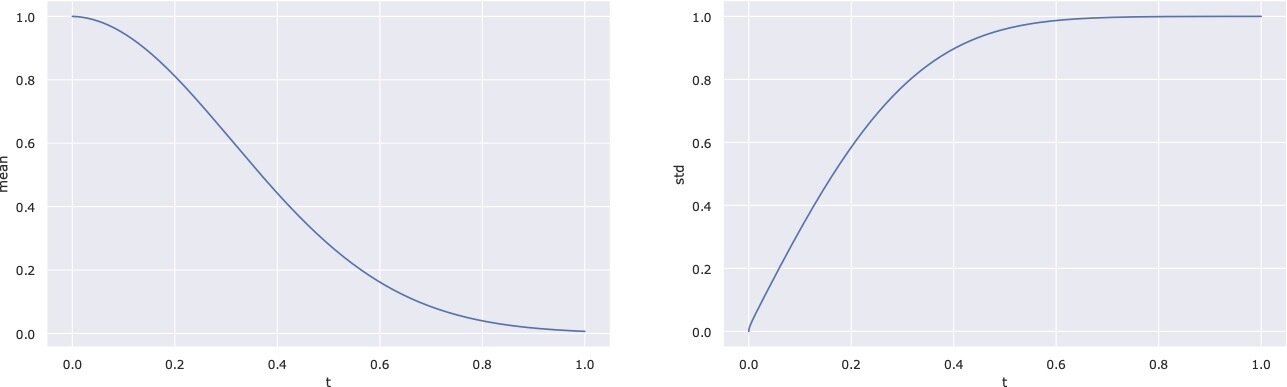
Unconditional Diffusion Model
DDPM Schedule
\[p(x_t \mid x_0) = \mathcal{N}(\sqrt{\alpha_t}x_0, (1 - \alpha_t)\mathbb{I}) \]
Unconditional Diffusion Model
Tweedie's formula
If \(x_i \sim \mathcal{N}(a_i~x_0, b_i^2 \mathbb{I})\), then
\[\hat{x}_0(x_t) = \mathbb{E}[x_0 \mid x_t] = \frac{x_t + b_i^2~\nabla_{x_t} \log p_t(x_t)}{a_i}\]
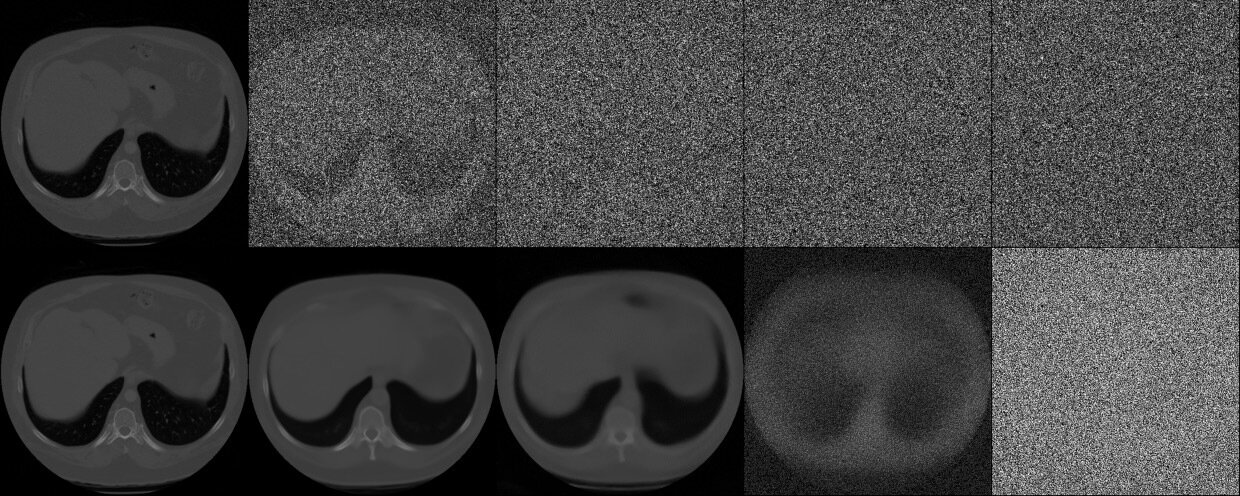
\(x_0\)
\(\hat{x}_0\)
\(t=0\)
\(t=1\)
Conditional Samples (Poisson vs Gaussian DPS)
DPS:
\[\nabla_{x_t} \log p(y \mid x_t) \approx \nabla_{x_t} \log p(y \mid \hat{x}_0(x_t))\]
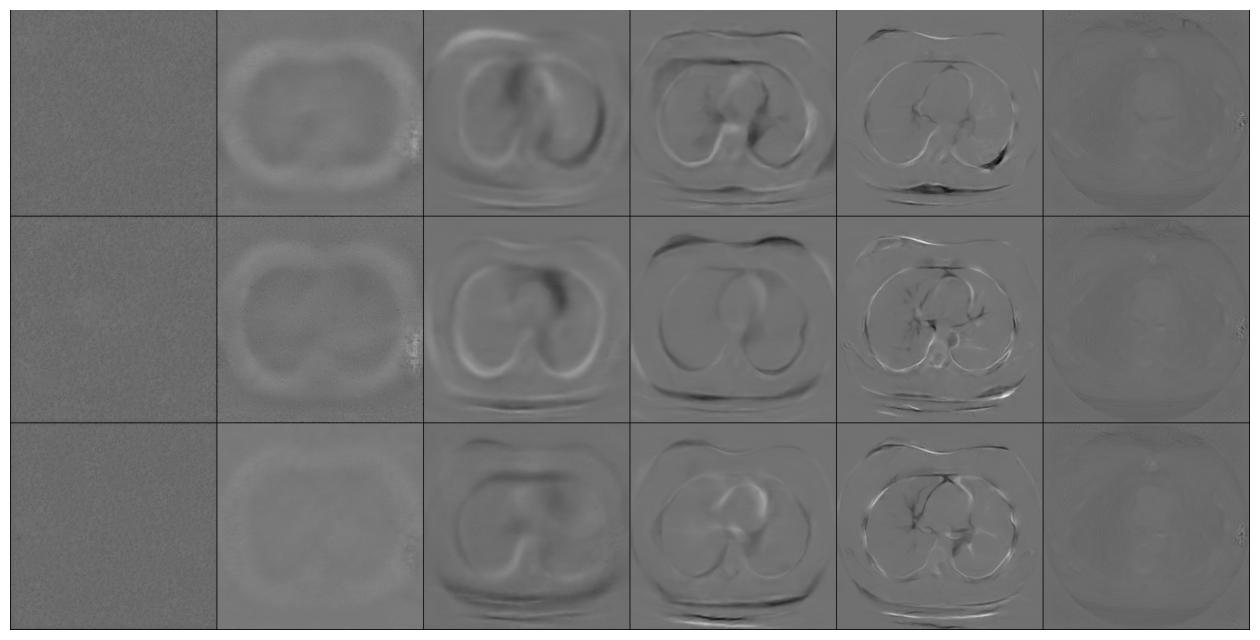
Poisson
Gaussian
Conditional Samples (Poisson vs Gaussian DPS)
DPS:
\[\nabla_{x_t} \log p(y \mid x_t) \approx \nabla_{x_t} \log p(y \mid \hat{x}_0(x_t))\]
Poisson
Gaussian
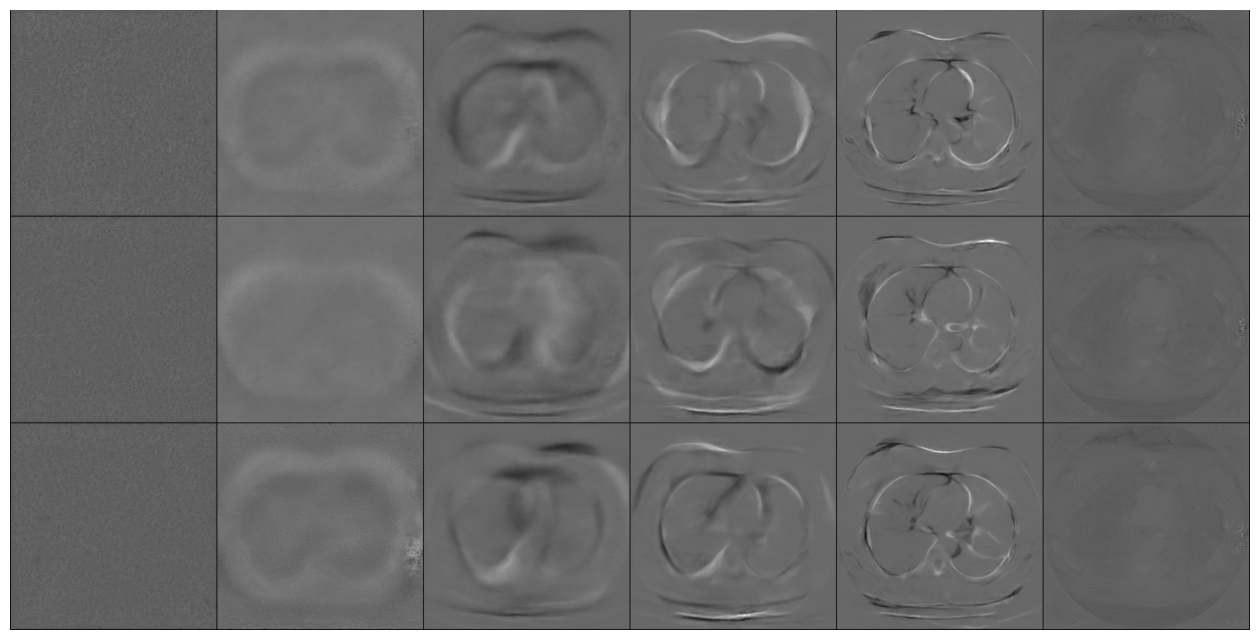
Conditional Samples (Poisson vs Gaussian DPS)
DPS:
\[\nabla_{x_t} \log p(y \mid x_t) \approx \nabla_{x_t} \log p(y \mid \hat{x}_0(x_t))\]
Poisson
Gaussian
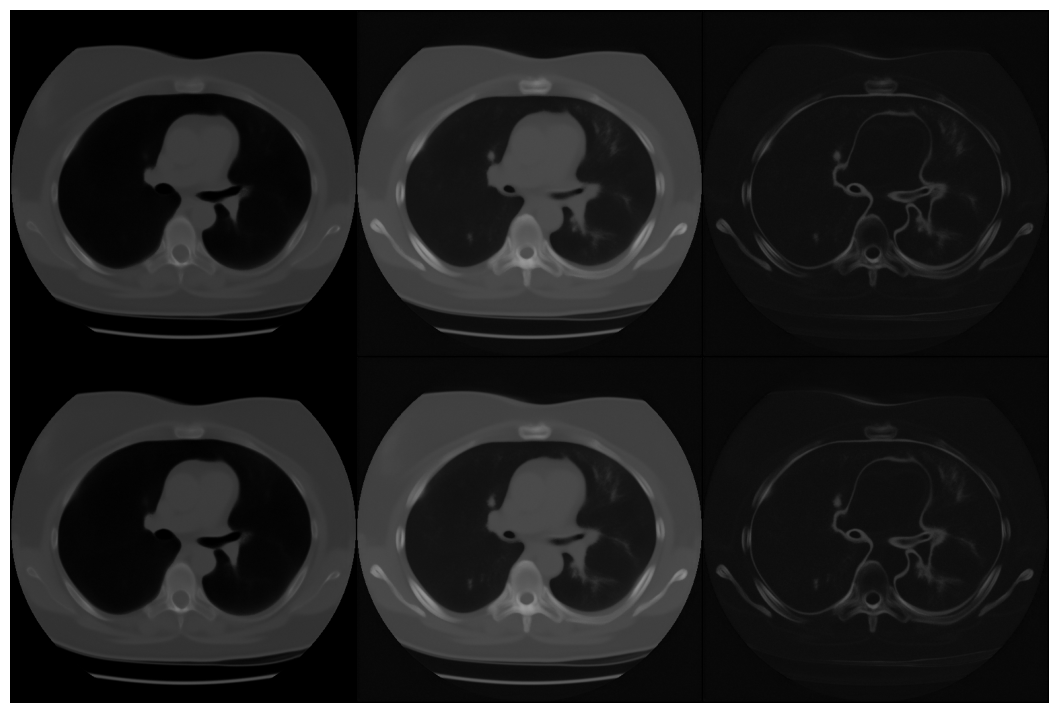
\(\hat{l}_{\alpha}\)
\(\hat{u}_{\alpha}\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
[10/10/23] Aim 3: Posterior Sampling and Uncertainty
By Jacopo Teneggi
