SHAP-XRT
The Shapley Value Meets
Conditional Independence Testing
Beepul Bharti, Jacopo Teneggi, Yaniv Romano, Jeremias Sulam
Explainable AI Seminars @ Imperial
5/30/2024
-
Reproducibility
-
Practical Accuracy
-
Explainability
-
Fairness
-
Privacy
[M. E. Kaminski, 2019]
E.U.: “right to an explanation” of decisions made
on individuals by algorithms
F.D.A.: “interpretability of the model outputs”
Responsible ML
Explanations in ML
{f}\huge(
{\huge)} = \text{\texttt{sick}}
- What parts of the image are important for this prediction?
- What are the subsets of the input so that
{f}(x_S) \approx {f}(x) ?
S \subseteq [n]
Explanations in ML
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual & causal explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..
Shapley values
efficiency
nullity
symmetry
-
exponential complexity
Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
Let be an - person cooperative game with characteristic function
G = ([n],f)
n
f : \mathcal P([n]) \mapsto \mathbb R
How important is each player for the outcome of the game?
\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\} } w_{S} \left[ f(S\cup \{i\}) - f(S) \right]
marginal contribution of player i with coalition S
Shap-Explanations
f(X) \approx \mathbb E[Y|X]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
x_S
x:
x_{S^c}
\tilde{X}_S:
Shap-Explanations
f(X) \approx \mathbb E[Y|X]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
x_S
x
\tilde{X}_S
Shap-Explanations
f(X) \approx \mathbb E[Y|X]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
\displaystyle \phi_i = \sum_{S\subseteq [n]\setminus \{i\}} w_S ~ \mathbb E \left[ f(\tilde X_{S\cup \{i\}}) - f(\tilde X_{S}) \right]
What does it mean for a feature to receive a high Shapley Value?
Precise Notions of Importance
Formal Feature Importance
H_{0,i}:~ X_S \perp\!\!\!\perp Y | X_{[n]\setminus S}
[Candes et al, 2018]
Do the features in \(S\) contain any additional information about the label \(Y\) that is not in the complement \({[n]\setminus S}\) ?
Precise Notions of Importance
Local Feature Importance
XRT: eXplanation Randomization Test
returns a valid p-value, \(\hat{p}_{i,S}\) for the test above
\text{reject} ~\Rightarrow~ i=2 \text{: important}
\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x
H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})
Precise Notions of Importance
Local Feature Importance
\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal{D}_x
H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})
\gamma_{i,S}
\displaystyle \phi_{\color{red}i}(x) = \sum_{S\subseteq [n]\setminus \{{\color{red}i}\}} w_{S} ~ \mathbb E \left[ f(\tilde X_{S\cup \{{\color{red}i}\}}) - f(\tilde X_S) \right]
Given the Shapley coefficient of any feature
Then
\mathbb{E}[\hat{p}_{i,S}]
and the (expected) p-value obtained for , i.e.
H^0_{i,S}
Theorem 1:
\mathbb{E}[\hat{p}_{i,S}] \leq 1 - \gamma_{i,S}.
i\in[n],
Teneggi, Bharti, Romano, and S. "SHAP-XRT: The Shapley Value Meets Conditional Independence Testing." TMLR (2023).
What does the Shapley value test?
H^0_{{\color{red}i},S}:~ f(\tilde X_{S\cup \{{\color{red}i}\}}) \overset{d}{=} f(\tilde X_{S})
\displaystyle H^0_\text{global,{\color{red}i}} = \underset{{S\subseteq [n]\setminus \{{\color{red}i}\}}}{\Large\cap} H^0_{{\color{red}i},S}
Given the Shapley value for the i-th feature, and
Theorem 2:
\displaystyle p_\text{global} = 2 \sum_{S \subseteq [n]\setminus i} w_{S} ~ \hat{p}_{i,S}
Then, under \(\displaystyle H^0_\text{global} \), \(p_{\text{global}}\) is a valid p-value and
\mathbb{E}[p_\text{global}] \leq 2( 1-\phi_i(x))
Full Spectrum of Tests
S
S
\(\hat{p}_{4,S}\)
\(\hat{p}_{2,S}\)
Testing Semantic Importance via Betting
Input features are not inherently
interpretable to users
So far
model
\[\hat{y} = f(x)\]
statistical importance of
\[x_j\]
input features \(x_j\)
\(\rightarrow\)
concepts \(c_j\)
Testing Semantic Importance via Betting
input features \(x_j\)
\(\rightarrow\)
concepts \(c_j\)
What are the important concepts for
the predictions of a model?
Global and local importance
Fixed predictor
Statistically-valid importance
Any set of concepts
Problem Setup
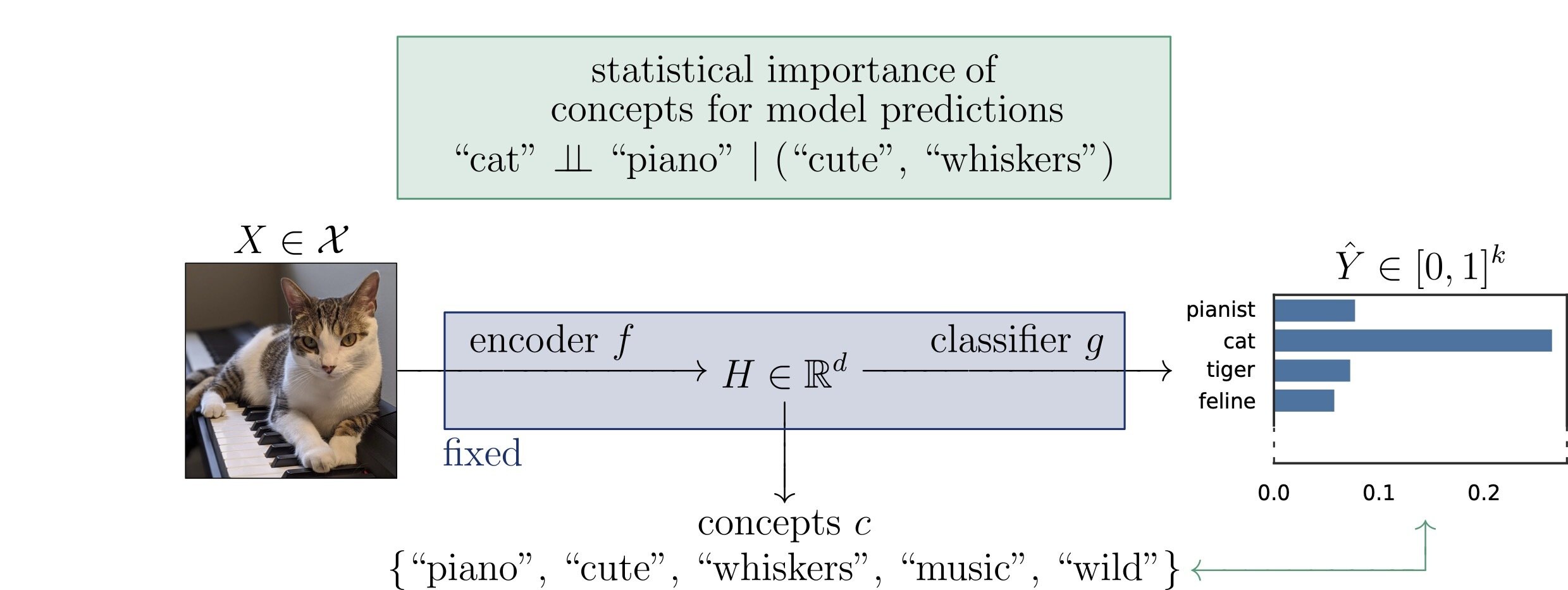
\(x \in \mathcal{X}\)
\(f:~\mathcal{X} \to \mathbb{R}^d\)
\(g:~\mathbb{R}^d \to [0, 1]^k\)
\(c \in \mathbb{R}^{d \times m}\)
input
encoder
classifier
concepts
\(Z = c^{\top} H\)
semantics
\(\hat{Y} = g(f(X))\)
predictions
\(H = f(X)\)
embeddings
Problem Setup
\(x \in \mathcal{X}\)
\(f:~\mathcal{X} \to \mathbb{R}^d\)
\(g:~\mathbb{R}^d \to [0, 1]^k\)
\(c \in \mathbb{R}^{d \times m}\)
input
encoder
classifier
concepts
\(Z = c^{\top} H\)
semantics
\(\hat{Y} = g(f(X))\)
predictions
\(H = f(X)\)
embeddings
FIXED
Defining Statistical Semantic Importance
For a concept \(j \in [m] \coloneqq \{1, \dots, m\}\)
type of dependence
marginal
over a population
global importance
\[H^{\text{G}}_{0,j}:~\hat{Y} \perp \!\!\! \perp Z_j\]
\(Z_j\)
\(\hat{Y}\)
Defining Statistical Semantic Importance
For a concept \(j \in [m] \coloneqq \{1, \dots, m\}\)
type of dependence
conditional
over a population
global conditional importance
\[H^{\text{GC}}_{0,j}:~\hat{Y} \perp \!\!\! \perp Z_j \mid Z_{-j}\]
\(Z_j\)
\(\hat{Y}\)
\(Z_{-j}\)
Defining Statistical Semantic Importance
For a concept \(j \in [m] \coloneqq \{1, \dots, m\}\)
type of dependence
conditional
for a specific input
semantic XRT
\[H^{\text{LC}}_{0,j,S}:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}\]
\(z_j\)
\(\hat{Y}\)
\(z_S\)
Testing by Betting
Null hypothesis \(H_0\), significance level \(\alpha \in (0,1)\)
Classical approach
collect data
analyze data
compute \(p\)-value
\(\rightarrow\)
\(\rightarrow\)
"Reject \(H_0\) if \(p \leq \alpha\)"
Sequential approach
Instantiate wealth process \(K_0 = 1\), \(K_t = K_{t-1} \cdot (1 + v_t\kappa_t)\)
"Reject \(H_0\) when \(K_t \geq 1/\alpha\)"
Testing by Betting
time
wealth
\(1/\alpha\)
under \(H_0\)
under \(H_1\)
rejection time \(\tau\)
Why Testing by Betting?
Data-efficient
Only use the data is needed to reject
Adaptive
The harder to reject, the longer the test
\[\downarrow\]
If concept \(c\) rejects faster than \(c'\)
then it is more important
Induces a natural rank of importance
Technical Intuition: SKIT
All definitions of semantic importance are two-sample tests
\[H_0:~P = \widetilde{P}\]
(Podkopaev et. al, '23)
Global importance (SKIT)
\(H^{\text{G}}_{0,j}\)
\(P_{\hat{Y} Z_j} = P_{\hat{Y}} \times P_{Z_j}\)
\(\iff\)
\(H^{\text{GC}}_{0,j}\)
Global conditional importance (c-SKIT)
\(\iff\)
\(P_{\hat{Y} Z_j Z_{-j}} = P_{\hat{Y} \widetilde{Z}_j, Z_{-j}},~\widetilde{Z}_j \sim P_{Z_j | Z_{-j}}\)
\(H^{\text{LC}}_{0,j,S}\)
Local conditional importance (x-SKIT)
\(\iff\)
\(P_{\hat{Y}_{S \cup \{j\}}} = P_{\hat{Y}_S} \)
Technical Intuition: SKIT
All definitions of semantic importance are two-sample tests
\[H_0:~P = \widetilde{P}\]
(Podkopaev et. al, '23)
Global importance (SKIT)
\(H^{\text{G}}_{0,j}\)
\(P_{\hat{Y} Z_j} = P_{\hat{Y}} \times P_{Z_j}\)
\(\iff\)
\(H^{\text{GC}}_{0,j}\)
Global conditional importance (c-SKIT)
\(\iff\)
\(P_{\hat{Y} Z_j Z_{-j}} = P_{\hat{Y} \widetilde{Z}_j, Z_{-j}},~\widetilde{Z}_j \sim P_{Z_j | Z_{-j}}\)
\(H^{\text{LC}}_{0,j,S}\)
Local conditional importance (x-SKIT)
\(\iff\)
\(P_{\hat{Y}_{S \cup \{j\}}} = P_{\hat{Y}_S} \)
novel procedures
ImageNet Classification with CLIP
global importance
ImageNet Classification with CLIP
global conditional importance
ImageNet Classification with CLIP
local conditional importance
Thank You!
Jeremias Sulam
Jacopo Teneggi
Yaniv Romano
Beepul Bharti
SHAP-XRT
IBYDMT
[Imperial XAI Seminar] SHAP-XRT
By Jacopo Teneggi
