How to Trust Your
Diffusion Model
Jacopo Teneggi, Jeremias Sulam
SPIE Photonics West 2024
January 28, 2024


A Step Back: Responsible ML
discriminative model
\(\rightarrow\)
input
prediction
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
\(\rightarrow\)
A Step Back: Responsible ML
discriminative model
\(\rightarrow\)
input
prediction
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
\(\rightarrow\)
Explaining with The Shapley Value
\(=\)
"hemorrhage"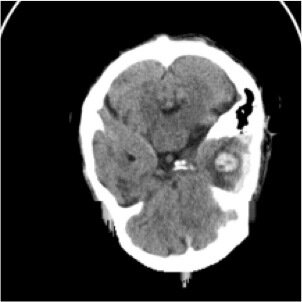
\(f\)
\((\)
\()\)
What are the important parts of
the image for this prediction?
JT, Alexandre Luster, JS (2021) "Fast Hierarchical Games for Image Explanations", TPAMI
JT*, Beepul Bharti*, Yaniv Romano, JS (2023) "SHAP-XRT: The Shapley Value Meets Conditional Independence Testing", TMLR
h-Shap
Efficient computation with accuracy guarantees
SHAP-XRT
Statistical meaning of
large Shapley Values
Explaining with The Shapley Value
Deploying these methods to inform
better practices in real-world scenarios
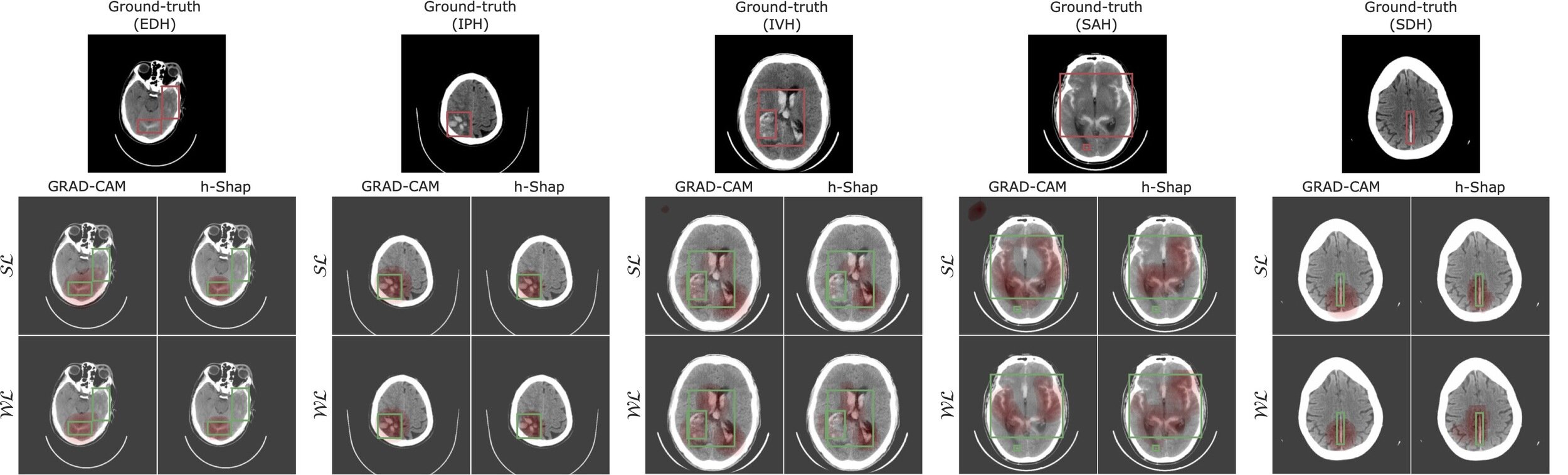
JT, Paul H Yi, JS (2023) "Examination-level Supervision for Deep Learning-based Intracranial Hemorrhage Detection on Head CT", Radiology: AI
A Different Scenario
generative
model
\(\rightarrow\)
input
samples
\(\rightarrow\)
For example:
- Large Language Models
- Text-to-image Diffusion Models
- Solving Inverse Problems Stochastically
A Different Scenario
generative
model
\(\rightarrow\)
input
samples
\(\rightarrow\)
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
Real-world
performance
Reproducibility
Explainability
Fairness
Privacy
?
Running Example: CT Denoising
For an observation \(y\)
\[y = x + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2\mathbb{I})\]
reconstruct \(x\) with
\[F(y) \sim \mathcal{Q}_y \approx p(x \mid y)\]
\(x\)
\(y\)
\(F(y)\)

Is the Model Right?




Contributions: \(K\)-RCPS
Conformal prediction
On the same observation
samples are concentrated
Conformal risk control
For future observations
ground-truth is close
Statistically-valid uncertainty
quantification with shortest intervals
JT, Matt Tivnan, J W Stayman, JS (2023) "How to Trust Your Diffusion Model: A Convex Optimization Approach to Conformal Risk Control", ICML
Calibrated Quantiles
Lemma For pixel \(j\)
\[\mathcal{I}(y)_j = \left[\text{lower}, \text{upper}\right]\]
provides entrywise coverage, i.e.
\[\mathbb{P}\left[\text{next sample}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
Definition For \(m\) samples and miscoverage level \(\alpha\)
\(0\)
\(1\)
\(\frac{\lfloor(m+1)\alpha/2\rfloor}{m}\)
\(\frac{\lceil(m+1)(1 - \alpha/2)\rceil}{m}\)
\(\mathcal{I}(y)\)
Calibrated Quantiles

\(x\)
\(y\)
lower
upper
interval
Risk Controlling Prediction Sets
Definition For risk level \(\epsilon\), failure probability \(\delta\)
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
\(0\)
\(1\)
\(\mathcal{I}(y)\)
\(x\)
ground-truth is
not contained
Risk Controlling Prediction Sets
Procedure For pixel \(j\)
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\forall \lambda' \geq \lambda,~\text{risk}(\lambda') \leq \epsilon\}\]
ground-truth is
contained
\(0\)
\(1\)
\(\mathcal{I}(y)\)
\(\lambda\)
\(x\)
Risk Controlling Prediction Sets
Definition For risk level \(\epsilon\), failure probability \(\delta\)
\[\mathbb{P}\left[\mathbb{E}\left[\text{number of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
Procedure For pixel \(j\)
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\forall \lambda' \geq \lambda,~\text{risk}(\lambda') \leq \epsilon\}\]
\[\downarrow\]
Using the same \(\lambda\) for all pixels is
suboptimal for interval length
\[\downarrow\]
Risk Controlling Prediction Sets
Definition For risk level \(\epsilon\), failure probability \(\delta\)
\[\mathbb{P}\left[\mathbb{E}\left[\text{number of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
Procedure For pixel \(j\)
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\forall \lambda' \geq \lambda,~\text{risk}(\lambda') \leq \epsilon\}\]
\[\downarrow\]
We want to find the shortest
intervals that control risk
\(K\)-RCPS: High-dimensional Risk Control
scalar \(\lambda \in \mathbb{R}\)
\(\rightarrow\)
vector \(\bm{\lambda} \in \mathbb{R}^d\)
\(\mathcal{I}_{\lambda}(y)_j = [\text{low} - \lambda, \text{up} + \lambda]\)
\(\rightarrow\)
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\)
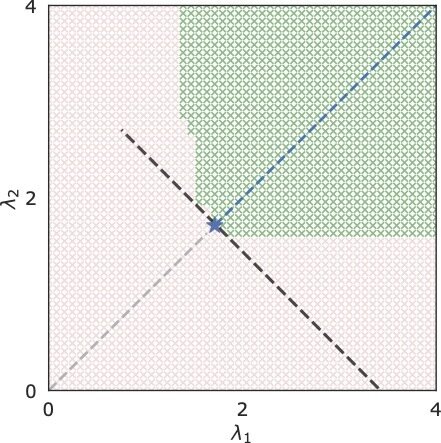
\(\rightarrow\)

RCPS \((\lambda_1 = \lambda_2 = \lambda)\)
RCPS
\(K\)-RCPS
gain
interval length
\(K\)-RCPS: The Procedure
1. Solve
\[\tilde{\bm{\lambda}}_K = \arg\min~\sum_{k \in [K]}n_k\lambda_k~\quad\text{s.t. empirical risk} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\forall \beta' \geq \beta,~\text{risk}(M\tilde{\bm{\lambda}}_K + \beta') \leq \epsilon\}\]
For a \(K\)-partition of the pixels \(M \in \{0, 1\}^{d \times K}\)

\(K=4\)
\(K=8\)
\(K=32\)
\(K\)-RCPS: Results


\(\hat{\lambda}_K\)
conformalized uncertainty maps
\(K=4\)
\(K=8\)
Thank You!

Jacopo Teneggi

Matt Tivnan

Web Stayman

Jeremias Sulam

GitHub Repo
[SPIE] K-RCPS
By Jacopo Teneggi
[SPIE] K-RCPS
- 151



