Aim 3: Posterior Sampling and Uncertainty
November 22, 2022
A common notion of uncertainty
original
perturbed
mean
std
A common notion of uncertainty
std
What does this measure of uncertainty tell us?
1. Regions of the reconstruction with higher variance
2. Range of where a new sample will be
3. How far the ground-truth image is
Our setting
1. The ground truth image
\[X \sim p(X)\]
2. The observation process
\[Y = X + v,~v \sim \mathcal{N}(0, \sigma^2 \mathbb{I})\]
3. The sampling procedure
\[Z = f(Y) \sim \mathcal{Q}_Y \approx p(X \mid Y)\]
Three sources of randomness
Our setting
\begin{vmatrix}
X_1 & X_2 & \dots & X_n \\
\hline
\overset{+v \sim \mathcal{N}(0, \sigma^2 \mathbb{I})}{\downarrow} & \downarrow & & \downarrow \\
Y_1 & Y_2 & \dots & Y_n \\
\hline
\overset{f(Y) \approx p(X \mid Y)}{\downarrow} & \downarrow & & \downarrow \\
Z_{1,1} & Z_{2,1} & & Z_{n,1} \\
\vdots & \vdots & & \vdots \\
Z_{1,m} & Z_{2,m} & & Z_{n,m}
\end{vmatrix}
original
perturbed
sampled
Question
Fix a pair \((x, y)\), and sample \(m\) times from \(f(y)\),
where will the \((m + 1)\)-th sample fall?
Conformal predictions
Coverage [Shafer and Vovk, 2008][Angelopoulos and Bates, 2022]
\[\mathbb{P}\left[Y_{\text{test}} \in \mathcal{C}(X_{\text{test}})\right] \geq 1 - \alpha\]
In our case, entrywise coverage
\[\forall j \in [d],~\mathbb{P}\left[f(y)_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
Theorem (Entrywise calibrated quantiles) Let \(\hat{l}_{\alpha},\hat{u}_{\alpha}\) be the \(\lfloor (m+1) \alpha/2 \rfloor / m\) and \(\lceil (m+1)(1 - \alpha/2) \rceil / m\) empirical quantiles of \(f(y)_j\) over \(m\) i.i.d. samples. Then,
\[\mathcal{I}(y)_j = [\hat{l}_{\alpha}, \hat{u}_{\alpha}]\]
provides entrywise coverage
Entrywise calibrated quantiles
original
\(\hat{l}_{\alpha}\)
\(\hat{u}_{\alpha}\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Entrywise calibrated quantiles
original
\(\hat{l}_{\alpha}\)
\(\hat{u}_{\alpha}\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Comparison of standard deviation with entrywise calibrated quantiles
std
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Calibrated quantiles distribution
\(Q_1\\ \Delta_{\text{HU}} \leq 7\)
\(Q_2\\\Delta_{\text{HU}} \in (7, 8]\)
\(Q_3\\\Delta_{\text{HU}} \in (8, 55]\)
\(Q_4\\\Delta_{\text{HU}} > 55\)
original
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Calibrated quantiles distribution
original
\(Q_1\\\Delta_{\text{HU}} \leq 7\)
\(Q_2\\\Delta_{\text{HU}} \in (7, 8]\)
\(Q_3\\\Delta_{\text{HU}} \in (8, 9]\)
\(Q_4\\\Delta_{\text{HU}} > 9\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Calibrated quantiles distribution
original
\(Q_3\\\Delta_{\text{HU}} \in (8, 34]\)
\(Q_4\\\Delta_{\text{HU}} > 34\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
\(Q_1\\\Delta_{\text{HU}} \leq 7\)
\(Q_2\\\Delta_{\text{HU}} \in (7, 8]\)
Calibrated quantiles distribution
original
\(Q_3\\\Delta_{\text{HU}} \in (8, 44]\)
\(Q_4\\\Delta_{\text{HU}} > 44\)
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
\(Q_1\\\Delta_{\text{HU}} \leq 7\)
\(Q_2\\\Delta_{\text{HU}} \in (7, 8]\)
Calibrated quantiles
What does this measure of uncertainty tell us?
1. Regions of the reconstruction with higher variance
2. Range of where a new sample will be
3. How far the ground-truth image is
\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
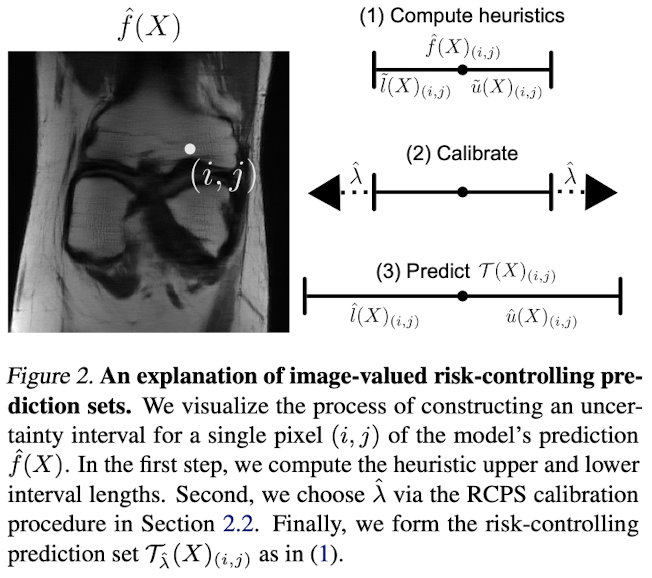
Risk control [Bates, 21]
For a pair \((x, y)\) define
\[\ell(x, \mathcal{I}(y)) = \frac{\#\{j \in [d]:~x_j \notin \mathcal{I}(y)_j\}}{d}\]
Definition (Risk-Controlling Prediction Set) A random set predictor \(\mathcal{I}:~\mathcal{Y} \to \mathcal{P}(\mathcal{X})\) is an \((\epsilon,~\delta)\)-RCPS if
\[\mathbb{P}\left[\mathbb{E}_{(X, Y)}\left[\ell(X, \mathcal{I}(Y)\right] \leq \epsilon\right] \geq 1-\delta\]
Image-to-Image Regression [Angelopolous, 22]
[11/22/22] Aim 3: Posterior Sampling and Uncertainty
By Jacopo Teneggi
