Aim 3: Posterior Sampling and Uncertainty
January 17, 2023


Where we left off: calibrated quantiles
1. The ground truth image
\[X \sim p(X)\]
2. The observation process
\[Y = X + v,~v \sim \mathcal{N}(0, \sigma^2 \mathbb{I})\]
(yes, simplistic for now, but the ideas will be general)
3. The sampling procedure
\[Z = f(Y) \sim \mathcal{Q}_Y \approx p(X \mid Y)\]
Three sources of randomness
Where we left off: calibrated quantiles
Fix a pair \((x, y)\), and sample \(m\) times from \(f(y)\),
where will the \((m + 1)\)-th sample fall?

Where we left off: calibrated quantiles
What does this measure of uncertainty tell us?
1. Regions of the reconstruction with higher variance
2. Range of where a new sample will be
3. How far the ground-truth image is








\(\hat{u}_{\alpha} - \hat{l}_{\alpha}\)
Recall:
\[\mathcal{I}(y)_j = [\hat{l}_\alpha, \hat{u}_\alpha],~\forall j \in [d]\]
Risk control [Bates, 21]
For a pair \((x, y)\) define
\[\ell(x, \mathcal{I}(y)) = \frac{\lvert\{j \in [d]:~x_j \notin \mathcal{I}(y)_j\}\rvert}{d}\]
Definition (Risk-Controlling Prediction Set) A random set predictor \(\mathcal{I}:~\mathcal{Y} \to \mathcal{P}(\mathcal{X})\) is an \((\epsilon,\delta)\)-RCPS if
\[\mathbb{P}\left[\mathbb{E}_{(X, Y)}\left[\ell(X, \mathcal{I}(Y)\right] \leq \epsilon\right] \geq 1-\delta\]
Risk control for diffusion models
Intuition
stretch calibrated quantiles until risk is controlled
Define
\[\mathcal{I}^\lambda(y) = [\hat{l}_\alpha - \lambda, \hat{u}_\alpha + \lambda],~\lambda \in \mathbb{R}\]

Risk control [Bates, 21]
For a calibration set \(\{(x_i, y_i)\}_{i=1}^n\) define
\[\hat{R}(\lambda) = \frac{1}{n} \sum_{i=1}^n \ell(x_i, \mathcal{I}^\lambda(y)),\quad R(\lambda) = \mathbb{E}[\hat{R}(\lambda)]\]
Definition (Upper Confidence Bound)
\[\mathbb{P}[R(\lambda) \leq \hat{R}^+(\lambda)] \geq 1 - \delta\]
which can be obtained via concentration inequalities
For example, via Hoeffding's inequality
\[\hat{R}^+(\lambda) = \hat{R}(\lambda) + \sqrt{\frac{1}{2n}\log(\frac{1}{\delta}})\]
Risk control [Bates, 21]
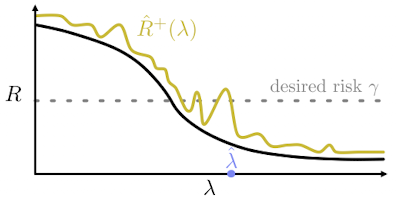
Calibration procedure
\[\hat{\lambda} = \inf \{\lambda \in \mathbb{R}:~\hat{R}^+(\lambda) \leq \epsilon,~\forall \lambda' \geq \lambda\}\]
[Bates, 21]
Results - before calibration


We calibrate on 256 images (128 samples each)
with \(\epsilon = 0.10, \delta=0.05\)
Results - before calibration


We calibrate on 256 images (128 samples each)
with \(\epsilon = 0.10, \delta=0.05\)
Risk is not controlled
Results - after calibration
We obtain
\[\hat{\lambda} \approx 8 \times 10^{-3} \approx 3 HU\]
need to increase the calibrated quantiles by \(\approx 6HU\)

Results - after calibration
We obtain
\[\hat{\lambda} \approx 8 \times 10^{-3} \approx 3 HU\]
need to increase the original calibrated quantiles by \(\approx 6HU\) in total

Risk is controlled
Results - some examples





\(\hat{u}_{\alpha} - \hat{l}_{\alpha} + 2\hat{\lambda}\)





original
Results
What does this measure of uncertainty tell us?
1. Regions of the reconstruction with higher variance
2. Range of where a new sample will be
3. How far the ground-truth image is








\(\hat{u}_{\alpha} - \hat{l}_{\alpha} + 2\hat{\lambda}\)
Open questions
1. Formal ways to minimize interval lengths
2. Current procedure does not guarantee entrywise risk-control
3. Current procedure is limited to choosing one value of \(\lambda\) for all features, which can be suboptimal
[01/17/23] Aim 3: Posterior Sampling and Uncertainty
By Jacopo Teneggi
[01/17/23] Aim 3: Posterior Sampling and Uncertainty
- 154



