Linear-time Solution of \[(\forall i)(XA_i-B_i Y=C_i)\]
Simultaneous Sylvester Equations
James B. Wilson, joint with Joshua Maglione

https://slides.com/jameswilson-3/quick-sylver/
Control Theory \(101-\varepsilon\)
Control System
- Given: system governed by diff-eq \[x'(t)=\mathsf{Model}(t,x(t), c(t))\] and observations \[y(t)=\mathsf{Obs}(t,x(t),c(t))\]
- Goal I: choose \(c(t)\) to "control" \(x(t)\) to desired states, at least as observed by \(y(t)\).
- Goal II: estimate \(x(t)\) from \(y(t)\).
Linear Time Independent (LTI) CS
\(\exists\) matrices \(A,B,C,D\) where \[x'(t)=\mathsf{Model}(t,x,c)=Ax(t)+Bc(t)\] \[y(t)=\mathsf{Obs}(t,x,c) = Cx(t)+Dc(t)\]
stabilizable if \(\exists\) matrix \(F\) \[c(t)=Fx(t)\] where \[x'(t)=Ax(t)+BFx(t)\] converges to "stable".
\(\exists\) matrices \(A,B,C,D\) where \[x'(t)=\mathsf{Model}(t,x,c)=Ax(t)+Bc(t)\] \[y(t)=\mathsf{Obs}(t,x,c) = Cx(t)+Dc(t)\]
stabilizable if \(\exists\) matrix \(F\) \(c(t)=Fx(t)\).
reduce (Schur Form) \[\begin{bmatrix} A & B\\ C & D\end{bmatrix}\sim\begin{bmatrix} I & A^{-1}B\\ 0 & G\end{bmatrix}\qquad G=D-CA^{-1}B\]
new problem \(\tilde{x}'(t)=H\tilde{x}(t)+Fy(t)+Gc(t)\) where \(H\) is Hurwitz: \(Re(\lambda)<0\) on \(\lambda\in Spec(H)\)
(LTI) Control System
Assume: \(\exists\) matrices \(A,B,C,D\) where \[x'(t)=\mathsf{Model}(t,x,c)=Ax(t)+Bc(t)\] \[y(t)=\mathsf{Obs}(t,x,c) = Cx(t)+Dc(t)\]
stabilizable if \(\exists\) matrix \(F\) \(c(t)=Fx(t)\)
Schur Form: \(G=D-CA^{-1}B\)
new problem \(\tilde{x}'(t)=H\tilde{x}(t)+Fy(t)+Gc(t)\) where \(H\) is Hurwitz: \(Re(\lambda)<0\) on \(\lambda\in Spec(H)\)
Luenberger: Estimate \(x(t)\) by solving for \(X\) \[HX-XA=-FC\] \(\|\tilde{x}(t)-Xx(t)\|\to 0\)
(LTI) Control System
LTI Control Systems
SOLVE FOR \(X\) IN \[HX-XA=-FC\]
Equation generalizes in shape hundreds of ways.
Really interested?
- Peter Benner's Control Theory Basics, in Handbook of Linear Algebra, Chapman & Hall, 2007
Solving \(XA-BY=C\)
Simplifying assumptions
- matrices are all approximately \(d\times d\)
- field operations are exact (numerical stability not considered here)
Case: \(B\) invertible
\[\begin{aligned} XA-BY &= C\\ Y & = B^{-1}(C+XA)\end{aligned}\]
So every \(X\) has a \(Y\).
Compute \(Y\) from \(X\) in \(O(d^3)\)-ops.
Case: \(B\) left-invertible
(tall-skinny \(B\) full rank)
\[\begin{aligned} XA-BY &= C\\ Y & = B^{\#}(C+XA)\end{aligned}\]
Again every \(X\) has a \(Y\).
Construct \(Y\) from given \(X\) in \(O(d^3)\)-ops.
Solving \(XA-BY=C\)
when \(X=Y\)?
Case: \(B\) invertible
\[\begin{aligned} XA-BX &= C & X & = B^{-1}(C+XA)\end{aligned}\]
...no clear solution.
Direct attack...
\[XA-BX = C\]
- System of linear equations: \[\begin{aligned}\sum_{\ell} X_{i\ell}A_{\ell k}-\sum_{m}B_{im}X_{mk}& =C_{ij}\\ (A^t\otimes I_d-I_d\otimes B)vec(X)& =vec(C)\end{aligned}\]
- \(d^2\) equations in \(d^2\) unknowns...\(O(d^6)\)-ops
d=1000 makes for exaflops of work!
100 Mega Watts @ 10 gigflops/Watt.
vs. 0.1 Watt for \(O(d^3)\) version.
Sylvester's Theorem: If \(A,B\) are square and have a common eigen value then \[(\exists ! X)(XA-BX=C).\]
By dimensions expect at most one solution, i.e. \(d^2\) equations in \(d^2\) unknowns.
Bartels-Stewart
Ways to get Spec(A)
Iteratively apply \(A\) to vector \(v\) till \(\exists\alpha_i\)\[\begin{aligned} A^{k+1} v& =\alpha_0 A^0v+\cdots +\alpha_k A^k v \\ ann_A(x) & = x^{k+1}-a_{k-1}x^{k-1}-\cdots -a_1 x^1 -a_0\end{aligned}\] Choices in how to (a) discover relation (b) apply relation.
- (Algebraic Lens) Krylov, Lanczos, Coppersmith, Weidemann,
- (Geometric Lens) QR, SVD,
- (Practical Lens) software has a button I can push.
Bartels-Stewart Theorem. There is an \(O(d^3)\)-time algorithm to solve \(XA-BX=C\).
Find Schur Decomposition
\[\begin{aligned} F^*AF & = \begin{bmatrix} I & * \\ 0 & \tilde{A}\end{bmatrix} & EBE^* & = \begin{bmatrix} I & * \\ 0 & \tilde{B}\end{bmatrix}\end{aligned}\]
Solve smaller system \[\tilde{X}\tilde{A}-\tilde{B}\tilde{X}=\tilde{C}\] and pull back through
\[EXAF+EBYF=ECF\]
Why did \(X=Y\) make solving so hard?
Why so few solutions?
\(X=Y\) shifts from one Sylvester system to a simultaneous system...
\[\begin{aligned} XA_1 -B_1 Y & = C_1\\ XA_2-B_2 Y & = C_2\end{aligned}\] where \(A_2=I_d, B_2=I_d,C_2=0\).
Same happens if \(X=X^t, \bar{X}^t\)
Real problem is to solve:
\[(\forall i)(XA_i - B_i Y=C_i)\]
\[(\forall i)(XA_i - B_i Y=C_i)\] in algebra
- Roth Removal Rule/Block-diagonalizing/Module direct sums \[\begin{bmatrix} I & -X \\ 0 & I \end{bmatrix}\begin{bmatrix} B_i & C_i\\ 0 & A_i \end{bmatrix}\begin{bmatrix} I & X\\ 0 & I\end{bmatrix}=\begin{bmatrix} B_i & 0\\ 0 & A_i\end{bmatrix}\]
- Endomorphisms of modules \[End(_R M)=\{ X\mid (\forall i)(XR_i=R_iX)\}\]
- Adjoint algebras \[\{(X,Y)\mid (\forall i)(XA_i=B_iY)\}\]
- Schneider conjecture: \(O(d^6)\) is the complexity
\[\sum_{\ell} X_{i\ell} A_{\ell jk} -\sum_{m}B_{im}Y_{mjk} =C_{ijk}\]
- \(d^2 e\) equations in \(2d^2\) variables, highly over determined (expect few to now solutions)
- Not very sparse: 1/d nonzeros;
- Random \(d^2\times d^2\) subsystem is basically random dense, so \(O(d^6)\)-ops to solve
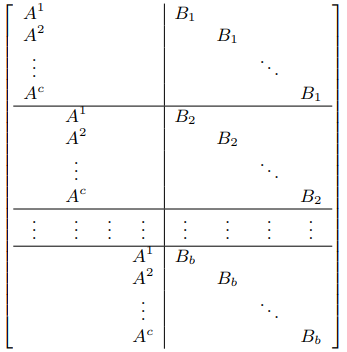
\(A^s=[A_{**s}]\) \(B_t=[B_{*t*}]\)
(Technically this is the matrix for a transposed version.)
Tempted to echelonize?
It Shave an order of magnitude, but fills in quick.
And yet a ton of symmetry...exploit this!
Solving
\[(\forall i)(XA_i - B_i Y=C_i)\]
In \(O(d^3)\) ops away from edge cases
It is a tensor problem
- \([A]=[A_1,\ldots,A_c]\in K^s\otimes K^b\otimes K^c\)
- \([B]=[B_1,\ldots,B_c]\in K^a\otimes K^t\otimes K^c\)
- \([C]=[C_1,\ldots,C_c]\in K^a\otimes K^b\otimes K^c\)
- Now under tensor contraction (generalized matrix multiplication) solve one tensor equation \[X [A]-[B]Y=[C]\]
Solution Scheme Repeat Bartels-Stewart
- Reduce dimension via operators \(E,F\) \[\begin{aligned} EX [A]F+E[B]YF & =E[C]F \\ \tilde{X}[\tilde{A}]+[\tilde{B}]\tilde{Y} & = \tilde{C}\end{aligned}\]
- Reconstruct solution from lower-dimensional solution
What is different?
- \(E,F\) are 4-tensors, denote \([[E]]\) (was 2-tensors) \[\begin{aligned} [[E]]X [A][[F]]+[[E]][B]Y[[F]] & =[[E]][C][[F]] \\ \tilde{X}[\tilde{A}]+[\tilde{B}]\tilde{Y} & = \tilde{C}\end{aligned}\]
- These are tensor contractions and it is quite incorrect to write as binary products, e.g. [A][[F]], we need new notation.
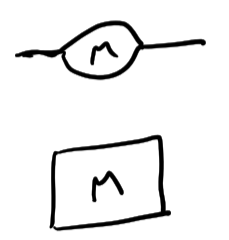
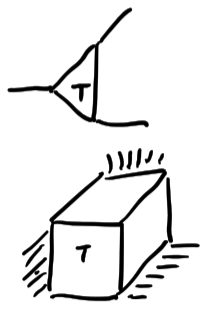
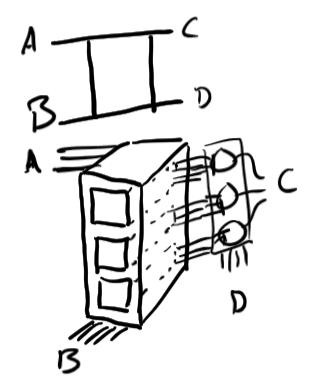
2-tensor/Matrix
3-tensor/list of matrices
4-tensor/Filing cabinet of spreadsheets
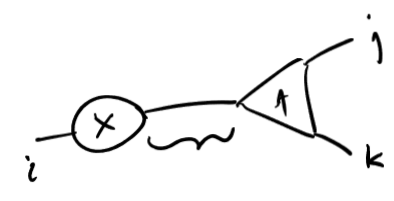
- for the dot-product \[\sum_{\ell} X_{i\ell} A_{\ell jk}\]
- more generally can replace dot-product with any bilinear form \(\langle|\rangle:U\times U\rightarrowtail K\)
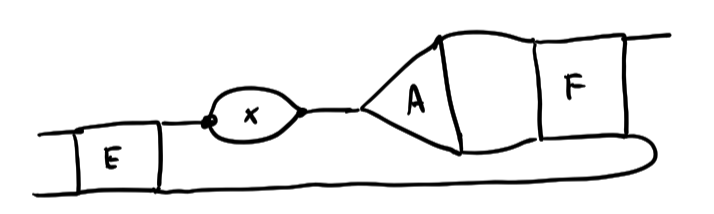
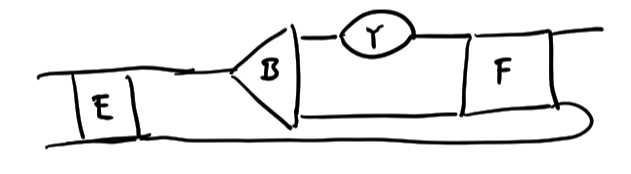
\([[E]]X[A][[F]]\)
\(-[[E]][B]Y[[F]]\)
\(=[[E]][C][[F]]\)
\[\begin{bmatrix} (A^1)^{-1} & \\ -(A^1)^{-1}A^2& I & & \\ \vdots & & \ddots & \\ -(A^1)^{-1} A^c & & & I\end{bmatrix}\begin{bmatrix} A^1\\ A^2 \\ \vdots \\ A^c\end{bmatrix}=\begin{bmatrix}A^1\\ 0\\ \vdots\\ 0\end{bmatrix}\]
Schur Decomposition in Matrix blowup

Schur Decomposition Tensorially
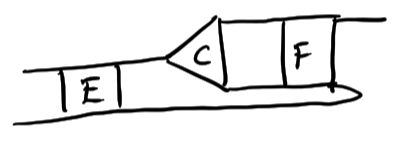
In tensor form...use face to clear the drawer (face elimination)
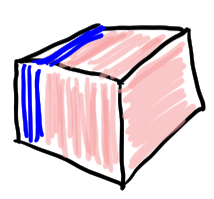
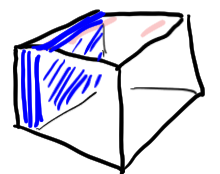
\[\begin{bmatrix} A_1^{-1} & \\ -A_1^{-1}A_2& I & & \\ \vdots & & \ddots & \\ -A_1^{-1} A_c & & & I\end{bmatrix}\begin{bmatrix} A_1\\ A_2 \\ \vdots \\ A_c\end{bmatrix}=\begin{bmatrix}A_1\\ 0\\ \vdots\\ 0\end{bmatrix}\]
In tensor form...use face to clear the drawer (face elimination)



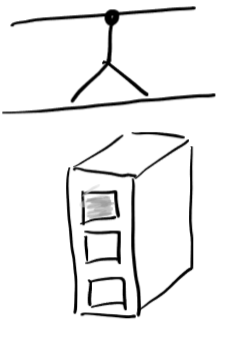
Controlled 4-tensor/Filing cabinet one drawer full
In tensor form...use face to clear the drawer (face elimination)




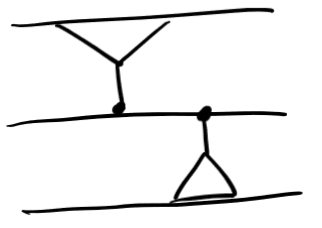
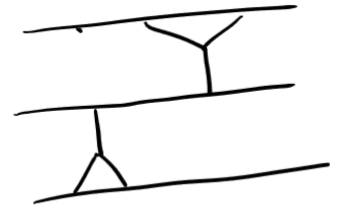
=
\([[E]]X[A][[F]]\)
\(-[[E]][B]Y[[F]]\)
\(=[[E]][C][[F]]\)
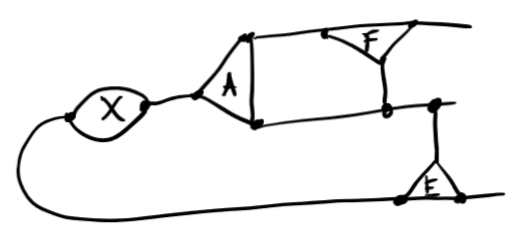
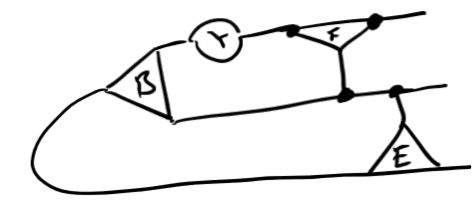
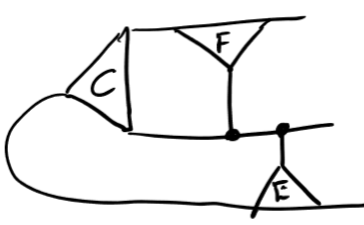
(As [[E]] slides past [[F]] we can face echelonize [B])
(Face echelonize [A] leaves a tiny system to solve)
Loose Ends...
- What if \(A_1\), \(B_1\) not invertible? Not Square
- Combine more than one slice.
- Tao's "Slice rank" is the metric
- Numerical Stability
- Implement and refine
Schneider's Problem: The actual complexity now is \(O(d^{3.5})\) to find one solution.
The takeaway
a tensor problem needs a tensor solution
QuickSylver
By James Wilson
QuickSylver
Linear time solution to simultaneous Sylvester equation solvers.
- 735



