Why are things different?
Verifiable Characterization of Characteristic subgroups
https://slides.com/jameswilson-3/what-is-difference/
James B. Wilson, Colorado State University
1. Show which graphs are the same.
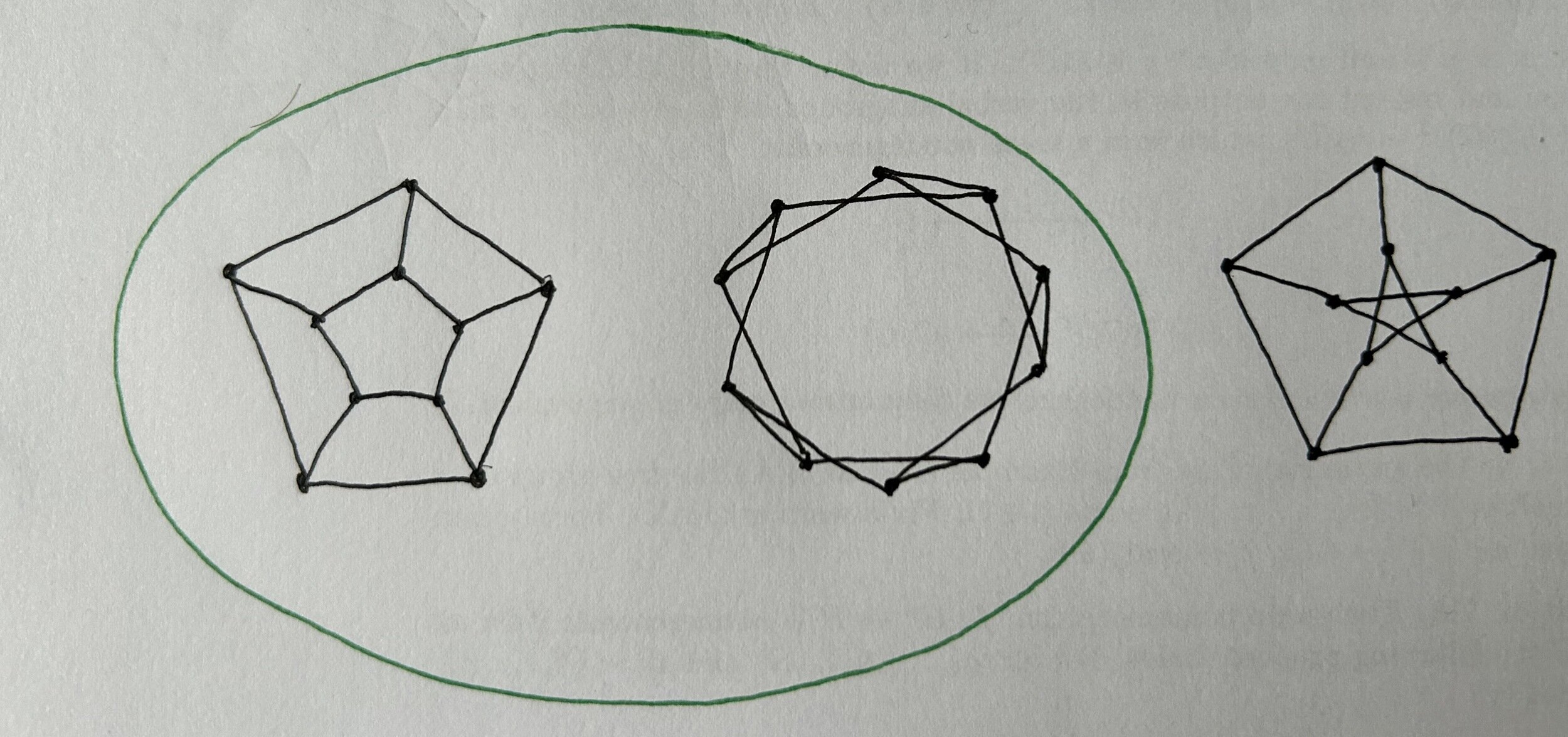
-4 Need to show how to build an isomorphism between these
2. Show which graphs are the same.
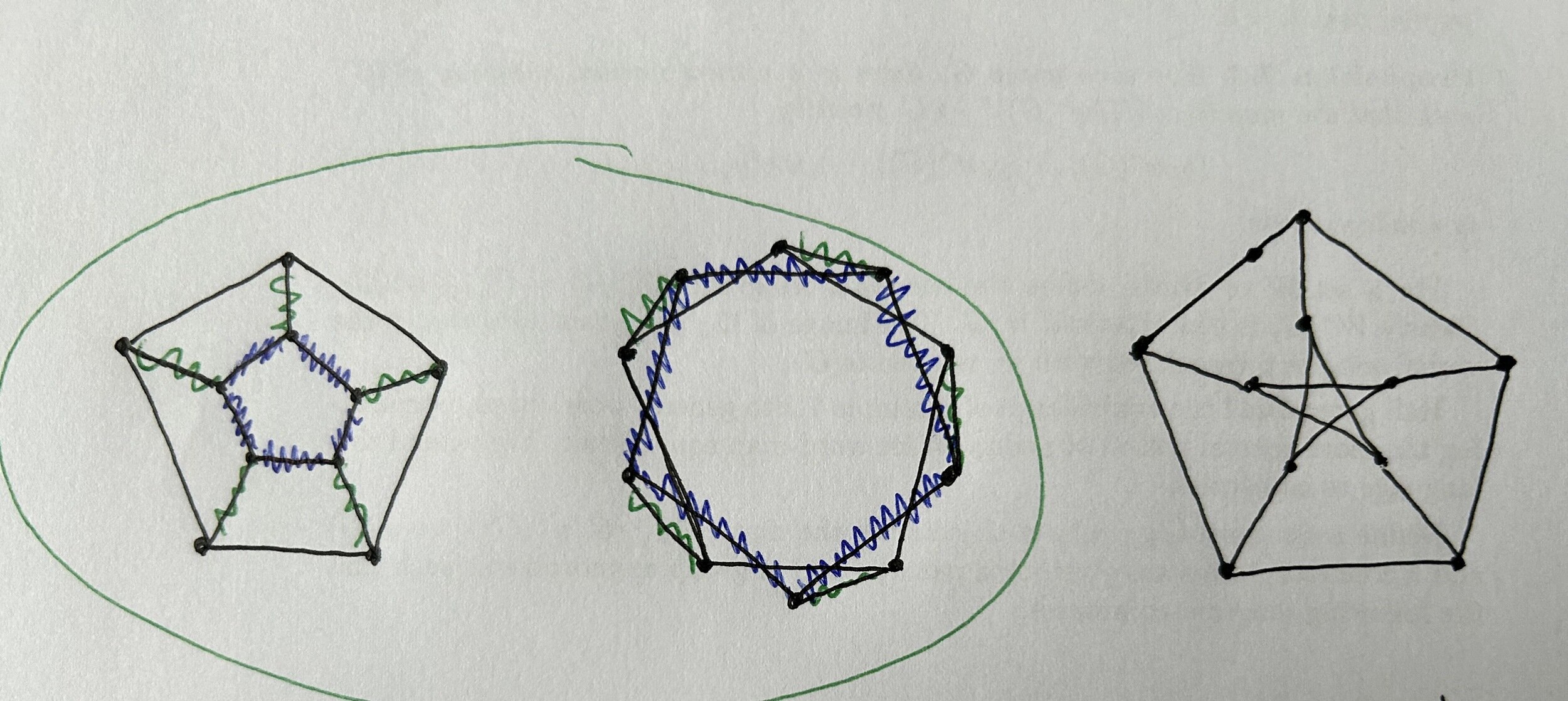
Great, maybe add labels to the different edges in the same color.
1. Show \(D_8\) is not the same as \(Q_8\).
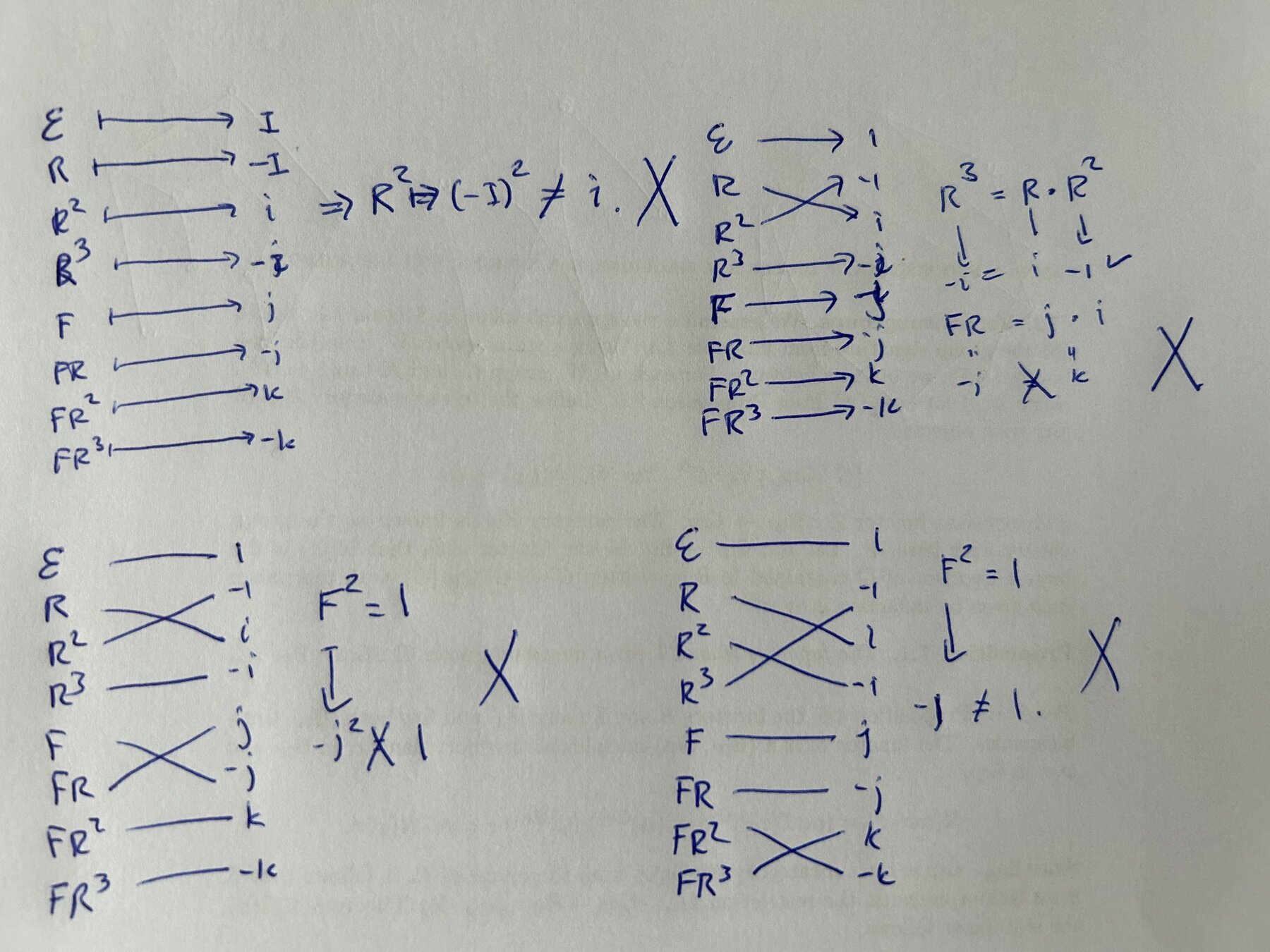
-4 need to identify different structure,
e.g count the number of elements of order 2
1. Show which graphs are the same.
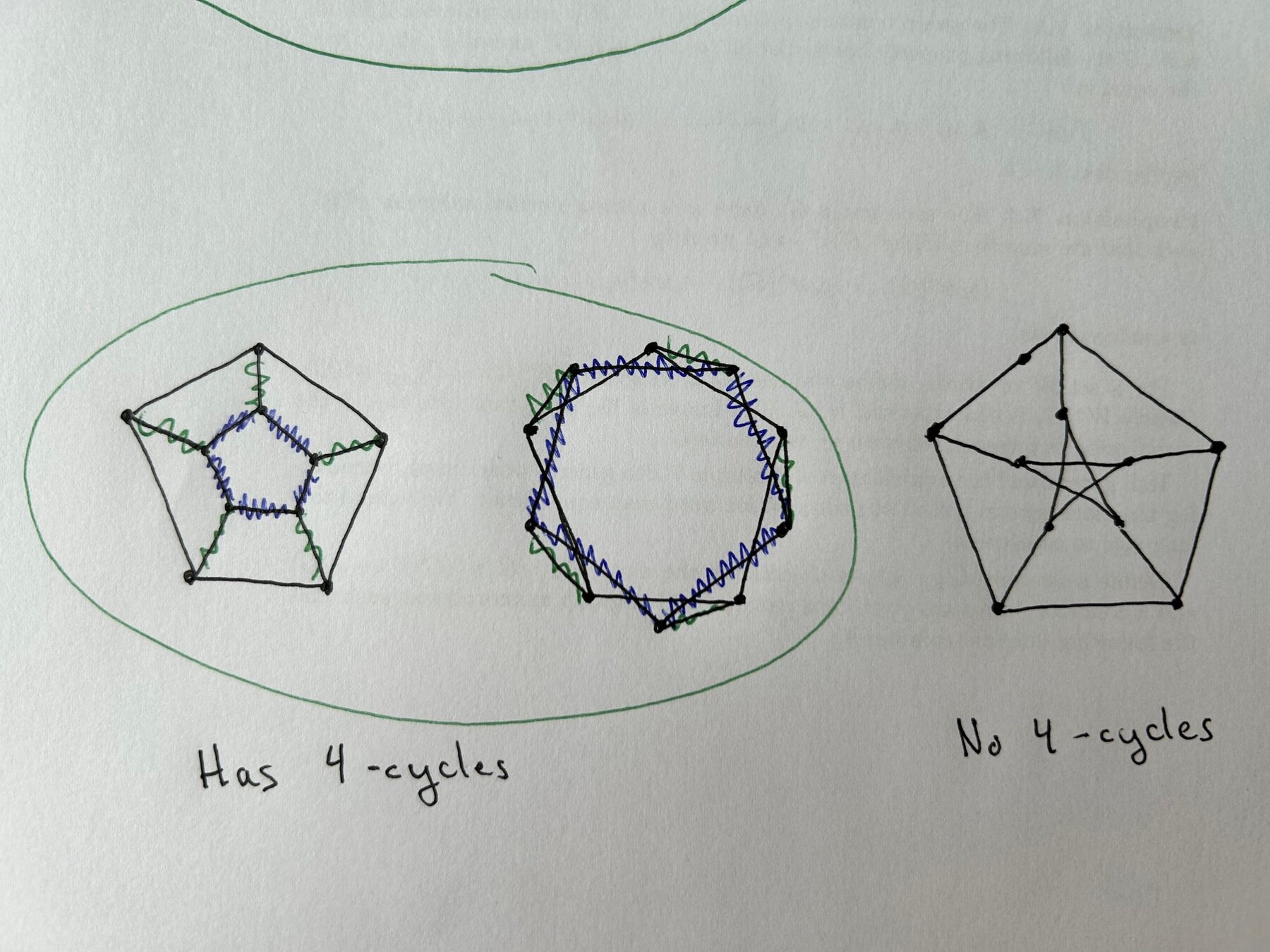
Great.
Moral
- For isomorphism we prefer a construction.
- For non-isomorphism we look for invariants.
- Set aside the fact that invariants often need isomorphisms internally, e.g. "without-loss-of-generality" is isomorphism you refuse to write.
Plan

Auckland
E. O'Brien
Meet the Team
Galway
J. Maglione
Bucknell
P. Brooksbank
H. Dietrich
Monash
why are things different?
- Structure?
structrualism
Things are different when they have different "structure", i.e. logical operations separate them.
Minimal assumptions
Need isomorphisms, i.e. a category
- Transitive/Product: \((x\cong y) \wedge (y\cong z)\to (x\cong z)\)
- Reflexive/Identity: \(x\to (x\cong x)\)
- Anti-symmetry/Inverses: \((x\cong y)\to (y\cong x)\)
Back to basics
- Equality means can replace like with like \[(x=y) \Rightarrow (\forall P)(P(x)\Leftrightarrow P(Y))\] (elimination/discharge rule of equality)
- Leibniz Law : Difference is about logical structure. \[X\neq Y \;\Rightarrow\; (\exists P)(P(X) \wedge \neg P(Y))\]
- Structuralism: "sameness is isomorphism" \[X\cong Y \;\Rightarrow\; X=Y\] (introduction rule of equality).
- Tarski-Thesis: Logical Operators = Isomorphism invariants.
- Fact. Logicism = Leibniz + Tarski Thesis \(\Longrightarrow \) Structuralism.
Invariants Are often misleading
It is often said:
"The character table is an invariant of finite groups."
What is "the" character table? This is non unique.
Reality
-
Replacing isomorphism? \[X\cong Y \Rightarrow I(X)\sim I(Y)\]
- becomes a tautology in the extreme
- needs complexity comparison
-
Isomorphism on more than the data?
- Assuming parameters. E.g. Jordan Normal Form classifies conjugacy of square matrices...but only if you agree on an order.
- In modal logic confusing \(\diamond P\) with \(\Box P\)?
Invariants
Definiton. In a category \(C\) an invariant is a functor \(I:C\to P\) into a partial order \(P=\langle P,\leq \rangle\)
Claim: Isomorphism invariant
\[X\cong Y \Rightarrow I(X)=I(Y)\]
is alway implied.
Invariants
Theorem (B-M-O'B-W)
- Every isomorphism invariant \(I:\overset{\leftrightarrow}{C}\to P\) induces a unique coarsets pre-order \(\leq\) on \(P\) such that \(I:C\to \langle P,\leq\rangle\) is a \(C\)-invariant.
- Univalence Axioms implies partial order.
- In a Cantor-Schroder-Bernstein category (e.g. finite groups, graphs, etc.) \(\langle P,\leq\rangle\) is a poset.
Invariants
Theorem (B-M-O'B-W)
Every* isomorphism invariant \(I:\overset{\leftrightarrow}{C}\to P\) is into a poset.
*Univalence/ Cantor-Schroder-Bernstein
Corollary. Isomorphism invariants define a distance function (pseudo-matric):
- \(d(u,u)=0\)
- \(d(u,v)=d(v,u)\)
- \(d(u,v)\leq d(u,w)+d(w,v)\)
\(u\cong v\Rightarrow d(u,v)=0\)

Distance induced by chromatic number of graph
Definition. An invariant \(I:C\to P\) is characteristic if for every automorphism \(\varphi\) of \(P\),
\[\varphi(I(X)) = X\]
A characteristic invariant is the only family of invariant that is solely about C (no parameters) and isn't replacing isomorphism.
Theorem (B-M-O'B-W) There are categories with
- objects \(|X|=|Y|\) and \(X\not\cong Y\)
- for every characteristic invariant \(I:C\to P\), \[I(X)=I(Y)\]
- Examples with graphs
- Examples with groups
- Examples with rings
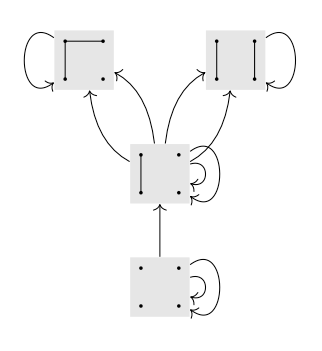
Toy Example: category of 4 vertex graphs <3 edges under inclusion
Easy invariants:
- Components? Not defining
- Degree sequence?
- ...not characteristic!
why are things different?
- Structure? Consistent \(\Leftrightarrow\) Incomplete
- Externalities?
Externality
Perhaps "structure" comes from outside.

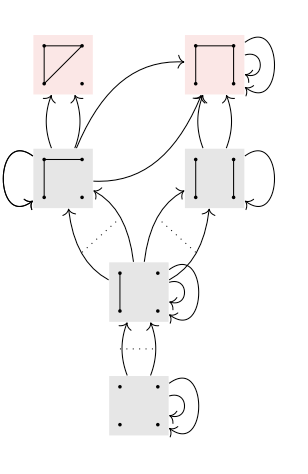
Break symmetry of invariants by extending context
What about groups?
Characteristic: \(H\leq G\) for every automorphism \(\varphi:G\to G\), \[\varphi(H)=H\]
Looks structural.
Rottlaender Type Groups:
\[\left\{\begin{bmatrix} \alpha & & u \\ & \alpha^u & v \\ & & 1 \end{bmatrix}\right\}\]
Has characteristic subgroups \[\left\{\begin{bmatrix} 1 & & u\\ & 1 & 0 \\ & & 1\end{bmatrix}\right\},\left\{\begin{bmatrix}1& & 0 \\ & 1 & v\\ & & 1 \end{bmatrix}\right\}\] but which is which? This is non-structural!
What about groups?
Characteristic: \(H\leq G\) for every automorphism \(\varphi:G\to G\), \[\varphi(H)=H\]
Looks structural.
Good Characteristic, e.g. commutator, come from external structure.
- Largest ABELIAN quotient.
- For free groups all char. come this way.
- What about the rest of group theory?
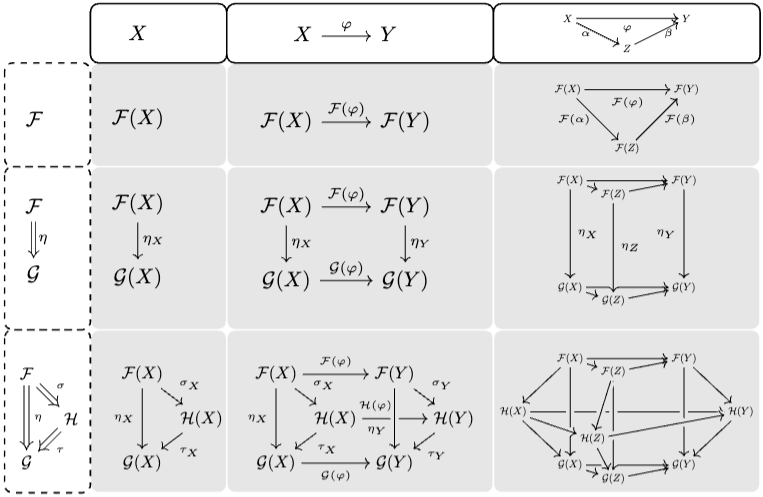
Cheat-sheet to 2-categories
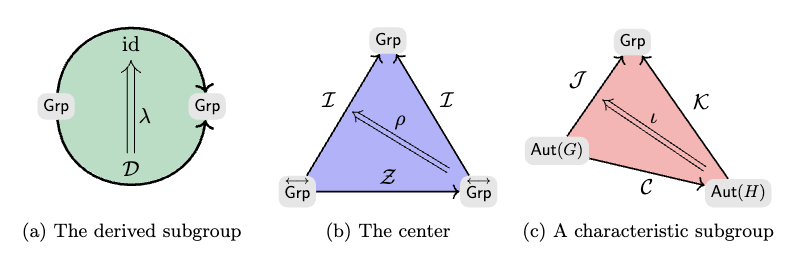
Characteristic Subgroups as Category Theory
Theorem (B-D-M-O'B-W)
\[\{\iota:H\hookrightarrow G \mid \iota(H)\text{ char. } G\}=\left\{\iota_G \mid \iota \in \text{Counital}\left(\overset{\longleftrightarrow}{Grp},Grp\right) \right\}\]
Furthermore, every counital is induced by a counit (e.g. all adjoints).
Category \(E\) with subcategory \(A\), \(I:A\hookrightarrow E\)
\[\text{Counital}\left(A,B\right)=\left\{\iota:C\Rightarrow I\right\}\]
Counit = counital with \(A=E, I=id_E\)
Corollary. All characteristic structure is external.
I.e. why a group \(G\) fixes a subgroup is the influence of some category.
Categories as rings
Most of categories today is written by topology and geometry.
We think algebra offers something different, and so did Freyd, Scedrov, and few others.
(Objective) Categories
bases Objects \(ob(C)\) a type of data
Morphisms: disjoint sets \(\hom_C(X,Y)\) for objects \((X,Y)\)
operators \(\circ:\hom_C(X,Y)\times \hom_C(Y,Z)\to \hom_C(X,Z)\)
\(1_X\in\hom_C(X,X)\)
rewriting for \(f:\hom_(X,Y), g\in \hom_C(Y,Z), h\in \hom_C(Z,W)\)
\[\begin{aligned} f1_X & = X \\ 1_Y f & = f\\ f(gh) & = (fg)h \end{aligned}\]
2 sorted second order theory
Objects have no axioms in category theory,
they are aren't needed.
Essentially Algebraic Structures (Eastern algebras)
base \(A\) a type of data
operators \([\ldots]:A^n\to A^?\) read as "maybe \(A\)"
guard rails polynomial formulas \(\Phi,\Upsilon\) in the operators where
\(\Phi(a_1,\ldots,a_n)=\Upsilon(a_1,\ldots,a_n)\;\Longrightarrow\;[a_1,\ldots,a_n]\text{ defined.}\)
rewriting e.g.\ associative when defined, identity when defined.
(Abstract) Categories
base \(A\) a type of data
operators \(\circ:A\times A\to A^?\) a partial product (\(A^?\) reads "maybe A")
\(\lhd(-):A\to A\) and \((-)\lhd:A\to A\)
guard rails \(a\lhd=\lhd\acute{a}\;\Longrightarrow\;a\dot{a}\text{ defined.}\)
rewriting
Summary: Set \(\mathbf{1}_{A}=\{a\lhd \mid a:A\}=\{\lhd a\mid a:A\}\) then
\[\begin{aligned} a(\dot a\ddot a) & = (a\dot a)\ddot a & \mathbf{1}_Aa & = \{a\}=a\mathbf{1}_A\end{aligned}\]
Categories = Monoids with some undefined products
\[\begin{aligned}\lhd(a\lhd) &=a\lhd & (\lhd a)\lhd & = \lhd a\\ \lhd(a\dot a) & =\lhd a & (a \dot a)\lhd & = \dot a\lhd\\ a(a\lhd) & = a & (\lhd a)a & = a \\ a(\dot a\ddot a)& =(a \dot a)\ddot a \end{aligned}\]
Category Theory's hidden Addition \(\sqcup\)
Given \(f\in\hom_C(X,Y)\) and \(g\in hom_C(X',Y')\) define
\[f\sqcup g:=\{f,g\}\subset \hom_C(X,Y)\cup \hom_C(X',Y')\]
Facts: Set \[A=\bigsqcup_{X,Y}\hom_C(X,Y)\] and identify \(f=\{f\}\)
- \(\sqcup\) is commutative, associative, with identity \(\emptyset\)
- \(\begin{aligned} f(h\sqcup g)& =fh\sqcup fg & (f\sqcup g)h & = fh \sqcup gh\end{aligned}\)
- \(f\emptyset = \emptyset=\emptyset f\)
- \(\mathbf{1}:=\{1_X \mid X:A\}\),* \[(\forall f:A\to B)\qquad f\mathbf{1}=\{f\}=\mathbf{1}f\]
- \(C\) is a partial associative unital distributive algebra (lacks negatives).
*In a hierarchy of sets or types.
Category Theory's hidden Addition \(\sqcup\)
Facts: Set \(A=\bigsqcup_{X,Y}\hom_C(X,Y)\) and identify \(f=\{f\}\)
\(A\) is a partial associative unital distributive algebra (lacks negatives).
Consequences. Categories \(A\) are much like rings.
- Identities \(e=f_Y, f=1_X\) are idempotents \(e=e^e, f=f^2\)
- Peirce decompositions \[eAf\cdot e'Af' \subset \begin{cases} eAf' & f=e'\\ \emptyset \end{cases}\]
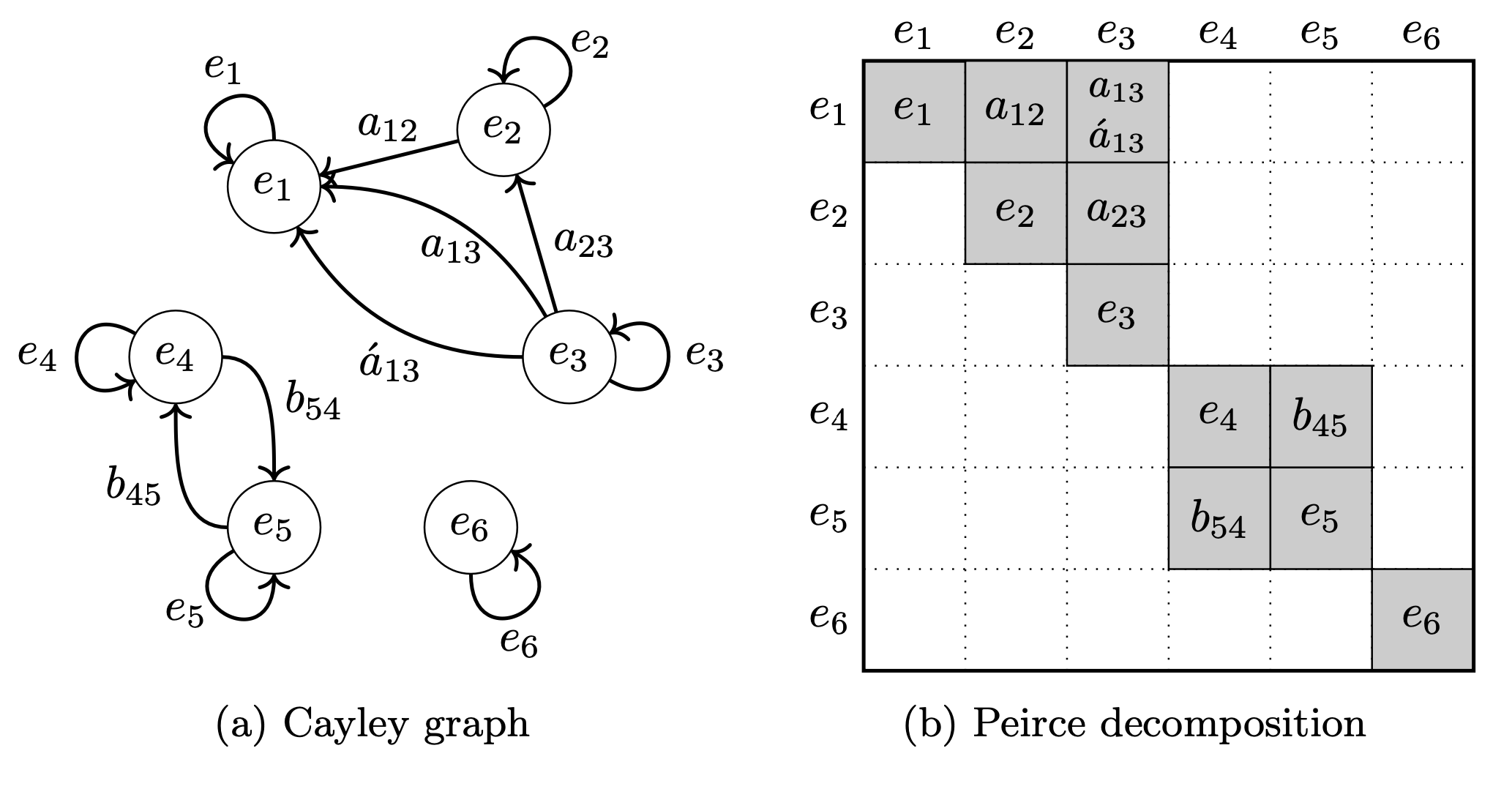
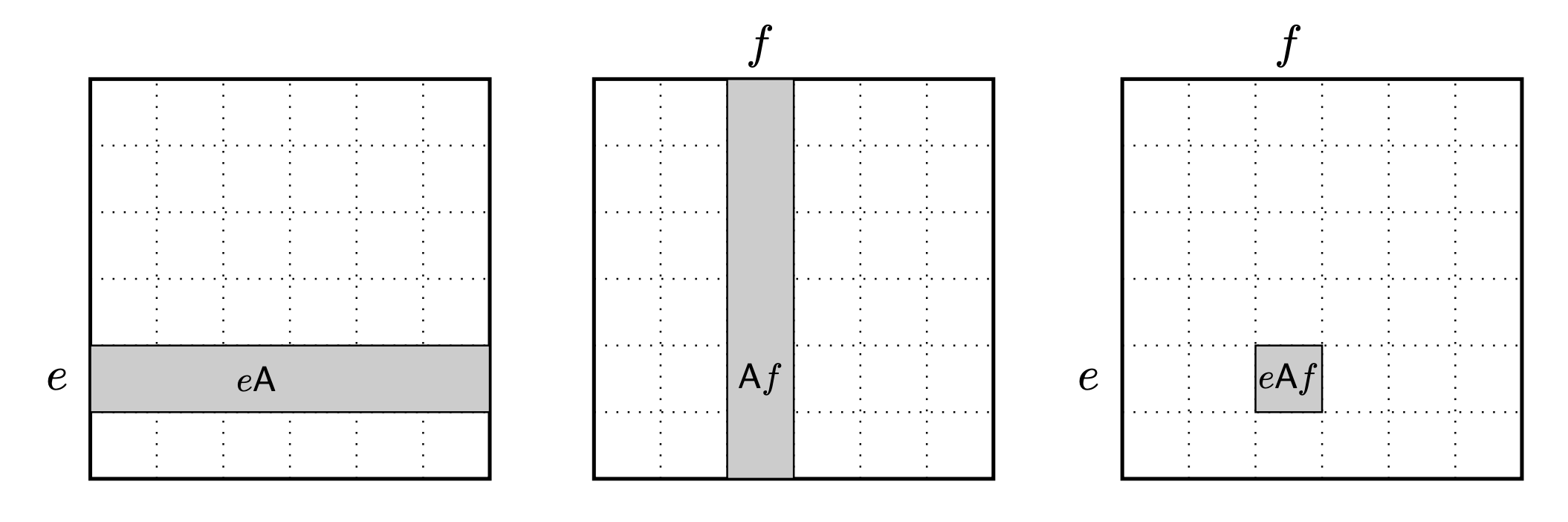
\[\mathbf{1}_A = \bigsqcup_{X:ob(C)} 1_X = \begin{bmatrix} 1 & & & \\ & 1 & & \\ & & \ddots & \\ & & & 1 \end{bmatrix}\]
Slice category
Coslice category
Hom-set
As rings have modules,
categories \(A\) have "capsules" \(X\)
\[\cdot:A\times X\to X^?\]
- \(a(\dot a x)=(a\dot a)x\)
- \(\mathbf{1}_A x=\{x\}\)
An \(A\)-morphism \[M:X\to Y^?\] where when the left-hand side is defined then \[M(ax)=aM(x)\]
In Peirce decomposition terms
\[\begin{bmatrix} & \vdots & \\ \cdots & A_{ij} & \cdots \\ & \vdots & \end{bmatrix} \begin{bmatrix} \vdots \\ x_j \\ \vdots\end{bmatrix}\]
Facts.
- Natural transformations \(\rho:G\Rightarrow F\) are bicapsules \(A\rho A\)
- Counits \(\rho:FG\Rightarrow I\) are \(A,B\)-morphisms \(M:A\to B\)
- Adjoints are pseudo-inverses \(M:A\to B\), \(N:B\to A\) \[MNM=M\qquad NMN=N\]
Extension Theorem in Category Theory Language.
In a category \(E\) of eastern algebras, given a counital \(\rho:C\Rightarrow I\) on a subcategory \(A\leq E\). If \(A\leq C\leq E\) and \(A\) is full in \(C\), then there exists a counital \(\sigma:D\Rightarrow J\) on \(C\).
Extension Theorem in Algebra Terms.
Set \(\Delta=A\rho A\). Then there is capsule \(\Upsilon\) where
\[\Delta\cong \text{Res}_A^C(\text{Ind}_A^C(\Delta))\otimes_A \Upsilon\]
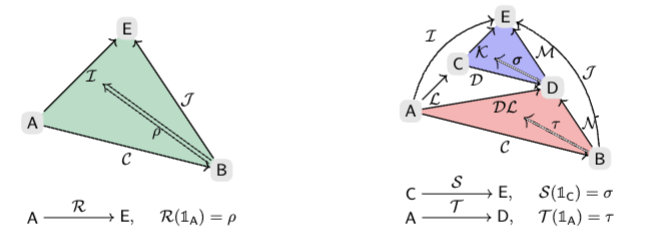
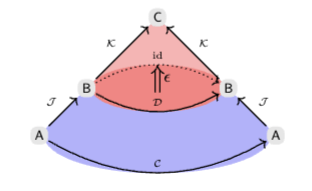
Corollary. All characteristic subgroups come from externalities.
Theorem.
- Internal counitals come from counits.
- Isoceles counitals extend to internal counits.
- Counitals of groups extend to isoceles counitals.
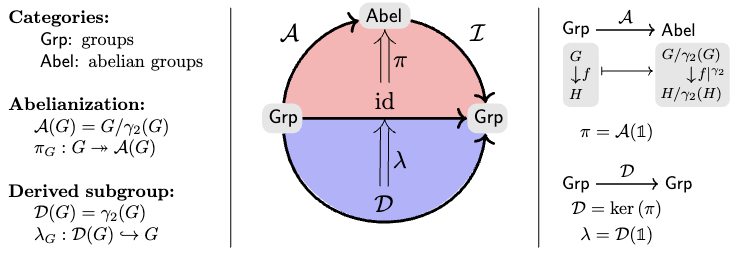
Commutator subgroup is the kernel of abelian adjunction (external)
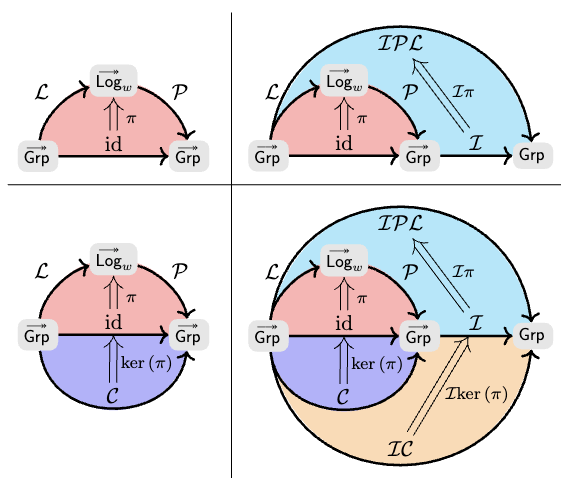
Maringal subgroups externalized by Varieties
why are things different?
- Structure? Consistent \(\Leftrightarrow\) Incomplete
- Externalities? Ramifies (splits into opposing reasons)
- Depends on your logic?
All our theorems have been done with minimal logic (Intuitionistic Martin-Lof). Consequence?
- Can explore alternative fixes, e.g. keep structuralims but remove Leibniz Law.
- Make all the work computational, e.g. certify characterisitc.
- Can pursue consistency in different extensions, e.g. 3-morphic.
- Leads to modeling isomorphism problems in computation with a 3-category
why are things different?
- Structure? Consistent \(\Leftrightarrow\) Incomplete
- Externalities? Ramifies (splits into opposing reasons)
- Depends on your logic? Yes, but new wrinkles not final answers.
- You don't have evidence they are equal.
Why are things different?
By James Wilson
Why are things different?
Why are things different? Explore the limits of structure and the external reasons for difference.
- 370



