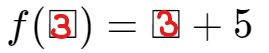Is a constant function ever the identity?
2021 James B. Wilson, Colorado State University
The brief story of trouble with substitution and why we need \(\lambda\)-calculus .
\(\lambda\)
Variables often treated as blanks to be filled. \[f(x) = x+5\]
becomes
...which becomes
In time the boxes are imaginary and substitution is immediate
\[f(3)=3+5\]
\[f(\Box)=\Box+5\]
Two simple functions emerge.
First are constant functions: \[\begin{aligned} f(x) & = 5\\ g(y) &= \pi \\ h(u) & = cat \end{aligned}\]
There are too many constant functions to name. So we capture them all with a \(c\) \[K_c(x)=c\]
Two simple functions emerge.
Second are the identity functions: \[\begin{aligned} f(x) & = x\\ g(y) & = y \\ h(u) & = u\end{aligned}\]
Though distinct in symbols, we find no difference when we substitute.
So we equate all these in a unified concept, a single identity function \[I(x)=x\]
Two simple functions emerge, and then provoke a protest.
Constant functions \(K_c(x)=c\) and the identity function \(I(x)=x\) should coexist in peace.
So what laws of substitution take control in a function such as \[K_x(x)=x?\]
Is this constant and never changing?
Or is it the identity---always reflecting the changes of the input?
Substitutions needs rules, but...
Making rules will impose limits and concern.
- Will banning some substitutions lead to loosing power, like recursion?
- Will the rules be consistent or lead to their own paradoxes?
- If the rules be consistent, will they be easy to follow?
- Will some substitutions never end?
Alonzo Church give us the answers in the form of his \(\lambda\)-calculus.
It was soon seen as equivalent to Turing's notion of computation.
In their honors today we teach
- The Turing Machine as the universal computer, and
- \(\lambda\)-calculus as the universal programming language.
Substitution: Why lambda-calculus?
By James Wilson
Substitution: Why lambda-calculus?
When we substitutes values into variables we seem to know intuitively that it makes sense. But with simple constant and identity functions we can soon run into paradoxes. This points at the need to define a theory of substitution known today as lambda-calculus.
